1.2 空间向量基本定理 课件(共11张PPT)
文档属性
| 名称 | 1.2 空间向量基本定理 课件(共11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 05:03:54 | ||
图片预览




文档简介
(共11张PPT)
延时符
复习巩固
延时符
第一章 空间向量与立体几何
1.2 空间向量基本定理
授课人: 日期:2023年8月7日
学 习 目 标
延时符
了解空间向量基本定理及其意义,会用基底表示空间向量。
3
掌握空间向量的正交分解
掌握用基向量解决立体几何中简单问题的通法
核心素养:数学抽象
数学运算 逻辑推理
4
延时符
新课导入
=+b
如图,设是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点O。
在对于任意一个空间向量, 设为所确定的平面上的投影向量,
则,
又向量,共线,
因此存在唯一的实数
使得=z, 从而z.
而在所确定的
平面上,由平面
向量基本定理可
知,存在唯一的
有序数对(),
使得 .
= , =
从而
Q
C
A
B
P
O
5
延时符
新课知识
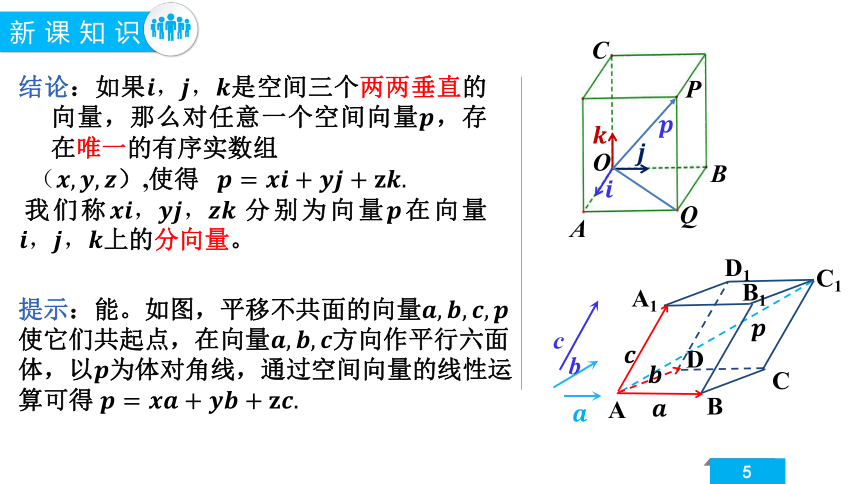
结论:如果是空间三个两两垂直的向量,那么对任意一个空间向量,存在唯一的有序实数组
),使得
我们称分别为向量在向量上的分向量。
提示:能。如图,平移不共面的向量使它们共起点,在向量方向作平行六面体,以为体对角线,通过空间向量的线性运算可得
A
D
C
B
A1
B1
C1
D1
b
c
Q
C
A
B
P
O
6
延时符
新课知识
一.空间向量基本定理
定理:如果三个向量 ,,不共面,那么对任意一个空间向量,
存在唯一的有序实数组 (x,y,z),使得=x+y+z.
把{,,}叫做空间的一个基底,,,叫做基向量.
①空间中任意三个不共面的向量都可以构成空间的一个基底.
②单位正交基底{}:基底中的三个基向量两两垂直,且长度都为1.
③把空间向量进行正交分解:把任意一个空间向量分解为三个两两垂直的向量, 即=x+y+z.
7
延时符
例题精讲
例1 如图,是四面体的棱的中点,点在线段上,点在线段上,且,用向量 表示.
用基底表示向量有三个步骤
(1)定基底:根据已知条件,
确定三个不共面的向量构成
空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结合相等向量的代换、向量的运算进行变形、化简,最后求出结果.
P
A
C
B
O
N
M
8
延时符
例题精讲
例2.如图,在平行六面体 ABCD-A1B1C1D1 中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N 分别为 D1C1,C1B1 的中点.求证 :MN⊥AC1.
9
延时符
课堂小结
1.基底的判断:若三个向量不共面,则可作为空间向量的一个基底.
①存在一个向量可以另外两个向量表示,则三向量共面;
②假设三向量共面,建立x,y的方程组,若无解,则不共面,若有解,则共面.
2.基底的构建:常依托正方体、长方体、平行六面体、四面体等几何体,用
从同一顶点出发的三条棱对应的向量为基底,并尽量选已知夹角和长度的向量.
3.用基底表示向量:结合向量的加减法运算法则寻找目标向量与基向量的关系.
4.基底的运用:用基底法解决立体几何中的垂直、共线、角度、模长等问题.
本课作业
必做 二
必做 一
必做 三
教材 15 页
1~4
三维 302页
11,12
2
01
02
03
谢
谢
聆
听
作者:梅河口市朝鲜族中学
2023年8月7日
延时符
复习巩固
延时符
第一章 空间向量与立体几何
1.2 空间向量基本定理
授课人: 日期:2023年8月7日
学 习 目 标
延时符
了解空间向量基本定理及其意义,会用基底表示空间向量。
3
掌握空间向量的正交分解
掌握用基向量解决立体几何中简单问题的通法
核心素养:数学抽象
数学运算 逻辑推理
4
延时符
新课导入
=+b
如图,设是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点O。
在对于任意一个空间向量, 设为所确定的平面上的投影向量,
则,
又向量,共线,
因此存在唯一的实数
使得=z, 从而z.
而在所确定的
平面上,由平面
向量基本定理可
知,存在唯一的
有序数对(),
使得 .
= , =
从而
Q
C
A
B
P
O
5
延时符
新课知识
结论:如果是空间三个两两垂直的向量,那么对任意一个空间向量,存在唯一的有序实数组
),使得
我们称分别为向量在向量上的分向量。
提示:能。如图,平移不共面的向量使它们共起点,在向量方向作平行六面体,以为体对角线,通过空间向量的线性运算可得
A
D
C
B
A1
B1
C1
D1
b
c
Q
C
A
B
P
O
6
延时符
新课知识
一.空间向量基本定理
定理:如果三个向量 ,,不共面,那么对任意一个空间向量,
存在唯一的有序实数组 (x,y,z),使得=x+y+z.
把{,,}叫做空间的一个基底,,,叫做基向量.
①空间中任意三个不共面的向量都可以构成空间的一个基底.
②单位正交基底{}:基底中的三个基向量两两垂直,且长度都为1.
③把空间向量进行正交分解:把任意一个空间向量分解为三个两两垂直的向量, 即=x+y+z.
7
延时符
例题精讲
例1 如图,是四面体的棱的中点,点在线段上,点在线段上,且,用向量 表示.
用基底表示向量有三个步骤
(1)定基底:根据已知条件,
确定三个不共面的向量构成
空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结合相等向量的代换、向量的运算进行变形、化简,最后求出结果.
P
A
C
B
O
N
M
8
延时符
例题精讲
例2.如图,在平行六面体 ABCD-A1B1C1D1 中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N 分别为 D1C1,C1B1 的中点.求证 :MN⊥AC1.
9
延时符
课堂小结
1.基底的判断:若三个向量不共面,则可作为空间向量的一个基底.
①存在一个向量可以另外两个向量表示,则三向量共面;
②假设三向量共面,建立x,y的方程组,若无解,则不共面,若有解,则共面.
2.基底的构建:常依托正方体、长方体、平行六面体、四面体等几何体,用
从同一顶点出发的三条棱对应的向量为基底,并尽量选已知夹角和长度的向量.
3.用基底表示向量:结合向量的加减法运算法则寻找目标向量与基向量的关系.
4.基底的运用:用基底法解决立体几何中的垂直、共线、角度、模长等问题.
本课作业
必做 二
必做 一
必做 三
教材 15 页
1~4
三维 302页
11,12
2
01
02
03
谢
谢
聆
听
作者:梅河口市朝鲜族中学
2023年8月7日
