山东省青岛市市北区2015届九年级上期中考试数学试题(无答案)
文档属性
| 名称 | 山东省青岛市市北区2015届九年级上期中考试数学试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 95.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-21 18:18:39 | ||
图片预览

文档简介
青岛市市北区2015届九年级上学期期中考试
等级
九年级数学
(考试时间:120分钟;满分:120分)
题号 一 二 三 四 合计
15 16 17 18 19 20 21 22 23 24
得分
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.
2.本试题共有24道题.其中1—8题为选 ( http: / / www.21cnjy.com )择题,请将所选答案的标号填写在第8题后面给出表格的相应位置上;9—14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15—24题请在试题给出的本题位置上做答.
得 分 评卷人 复核人 一、选择题(本题满分24分,共有8道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个 ( http: / / www.21cnjy.com )结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1—8各小题所选答案的标号填写在第8小题后面给出表格的相应位置上.
1. 对于四条线段a、b、c、d,如果ab=cd,那么( ).
A. = B. = C. = D. =
2. 根据下列表格对应值:
1.1 1.2 1.3 1.4
-0.59 0.84 2.29 3.76
判断关于的方程的一个解的范围是( ).
A. 1.1<<1.2 B.1.2<<1.3.
C. 1.3<<1.4 D. 无法判定
3.小明从一定高度随机掷一枚质地均匀的硬币 ( http: / / www.21cnjy.com ),他已经掷了两次硬币,结果都是“正面朝上”,那么,从概率的角度分析,小明第三次掷硬币时, ( ).
A. 一定会正面朝上; B. 正面朝上的可能性大于反面朝上;
C. 反面朝上的可能性大于正面朝上; D. 正、反面朝上的可能性一样大.
4.在平行四边形、菱形、矩形、正方形这四种图形中,既是轴对称图形,也是中心对称图形的有( ).
A.1种 B.2种 C.3种 D.4种
5.用配方法解方程时,配方后所得的方程为( ).
A. ; B.
C. D. .
6.主持人站在舞台的黄金分 ( http: / / www.21cnjy.com )割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是( ).
① AB:AC=AC:BC; ② AC≈6.18米;
③ 米; ④米或米
A.①②③④ B.①②③ C.①③ D.④
7.小亮和小刚按如下规则做游戏:每人从1,2,…,12中任意选择一个数,然后两人各掷一次均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负. 从概率的角度分析,游戏者事先选择( )获胜的可能性较大.
A.5 B.6 C.7 D.8
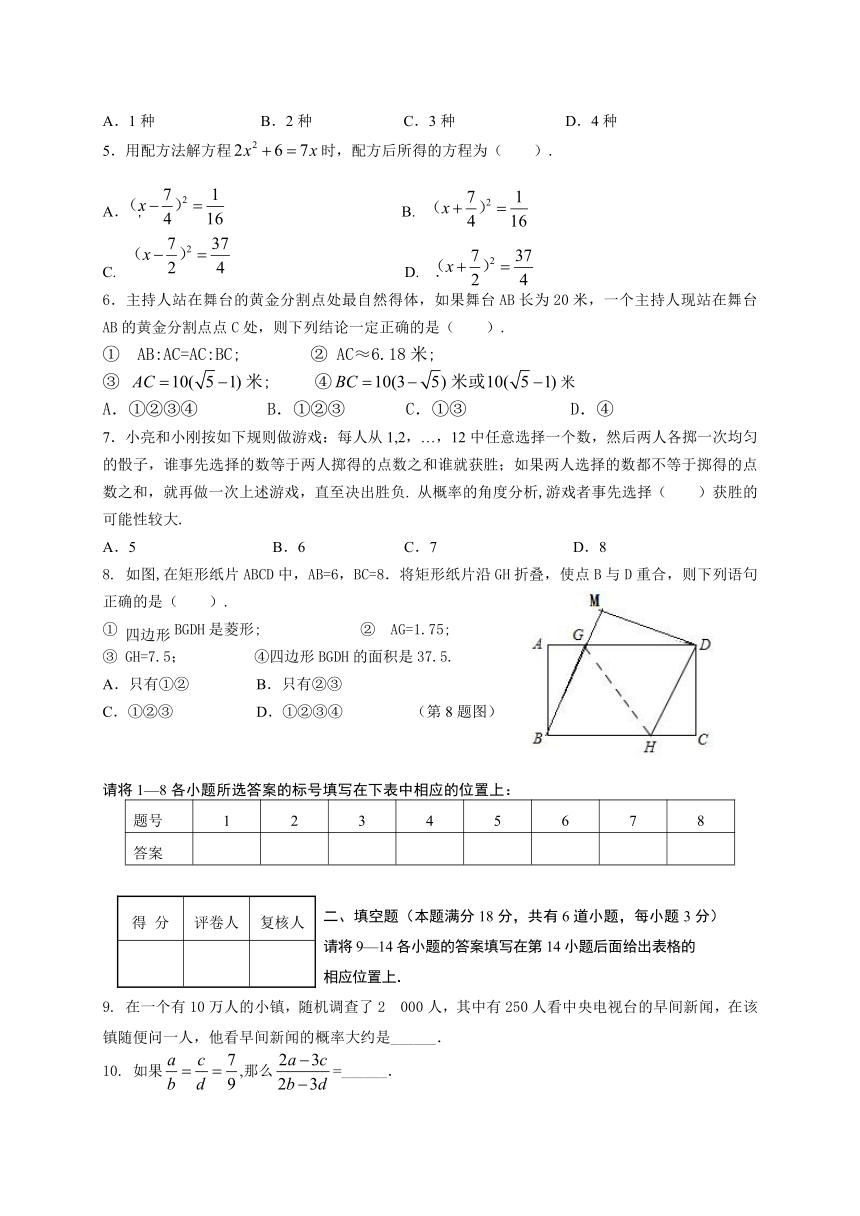
8. 如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( ).
① 四边形BGDH是菱形; ② AG=1.75;
③ GH=7.5; ④四边形BGDH的面积是37.5.
A.只有①② B.只有②③
C.①②③ D.①②③④ (第8题图)
请将1—8各小题所选答案的标号填写在下表中相应的位置上:
题号 1 2 3 4 5 6 7 8
答案
得 分 评卷人 复核人 二、填空题(本题满分18分,共有6道小题,每小题3分)请将9—14各小题的答案填写在第14小题后面给出表格的相应位置上.
9. 在一个有10万人的小镇,随机调查 ( http: / / www.21cnjy.com )了2 000人,其中有250人看中央电视台的早间新闻,在该镇随便问一人,他看早间新闻的概率大约是______.
10. 如果,那么=______.
11. 某种型号的电视机经过两次降价,价格从原来每台2250元降为每台1440元,设平均每次下降的百分率为,根据题意,可列方程为 .
12. 已知关于x的方程2-4x+m=0的一个根是1-,则它的另一个根是 .
13. 在菱形ABCD中,对角线A ( http: / / www.21cnjy.com )C 、BD相交于点O, BD=6 ,∠ABC =2∠BCD,则对角线AC= .,菱形ABCD面积= .
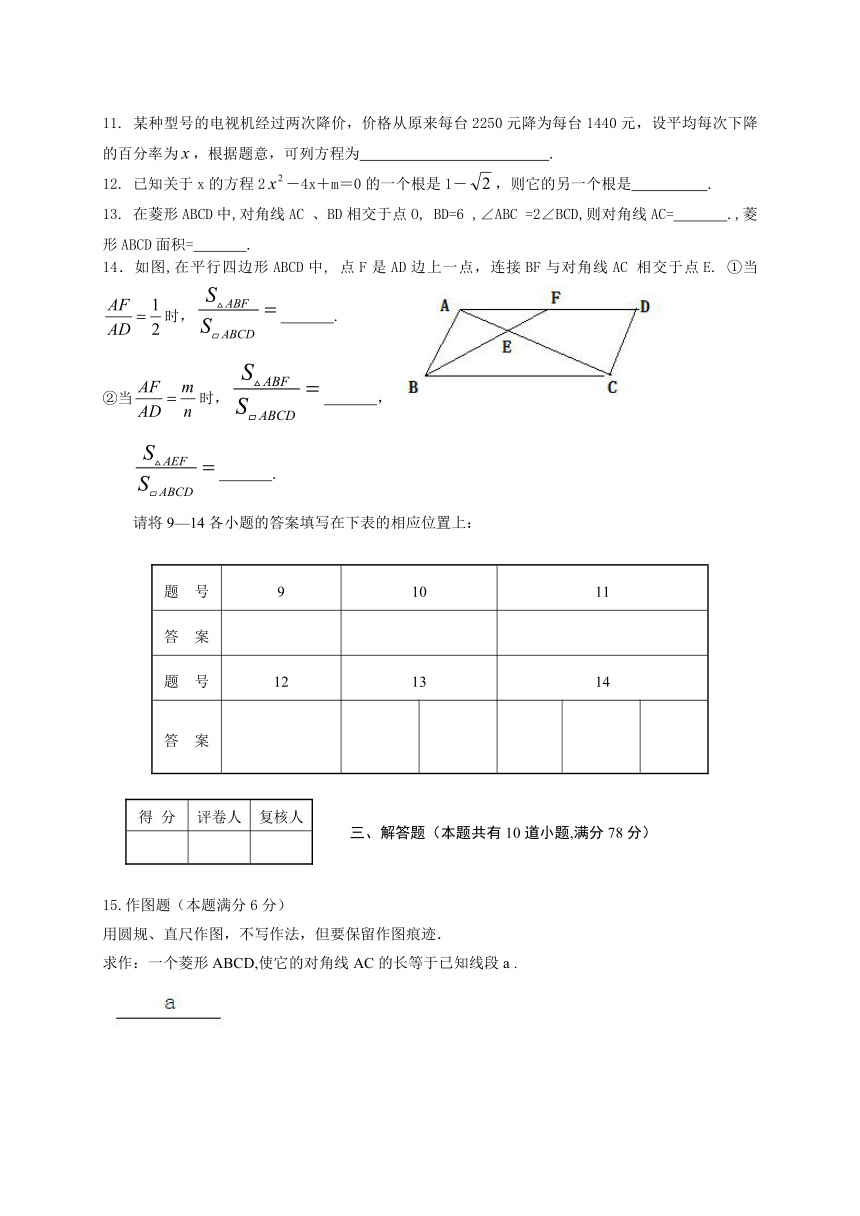
14.如图,在平行四边形ABCD中, 点F是AD边上一点,连接BF与对角线AC 相交于点E. ①当时, .
②当时, ,
.
请将9—14各小题的答案填写在下表的相应位置上:
题 号 9 10 11
答 案
题 号 12 13 14
答 案
得 分 评卷人 复核人 三、解答题(本题共有10道小题,满分78分)
15.作图题(本题满分6分)
用圆规、直尺作图,不写作法,但要保留作图痕迹.
求作:一个菱形ABCD,使它的对角线AC的长等于已知线段a .
结论:
16.(本题满分6分)解方程: 17.(本题满分6分)解方程:
16y2 + 8y-3 = 0 x(x+2)= 2 + x
解: 解:
18. (本题满分6分)
在方格纸上任意连接不在同一直线上的三个
格点,便可画出一个三角形. 请用这种方式在
如下的方格纸上画出两个大小不等的三角形,
要求这两个三角形都与格点三角形⊿ABC相
似,且相似比不为1.
结论:
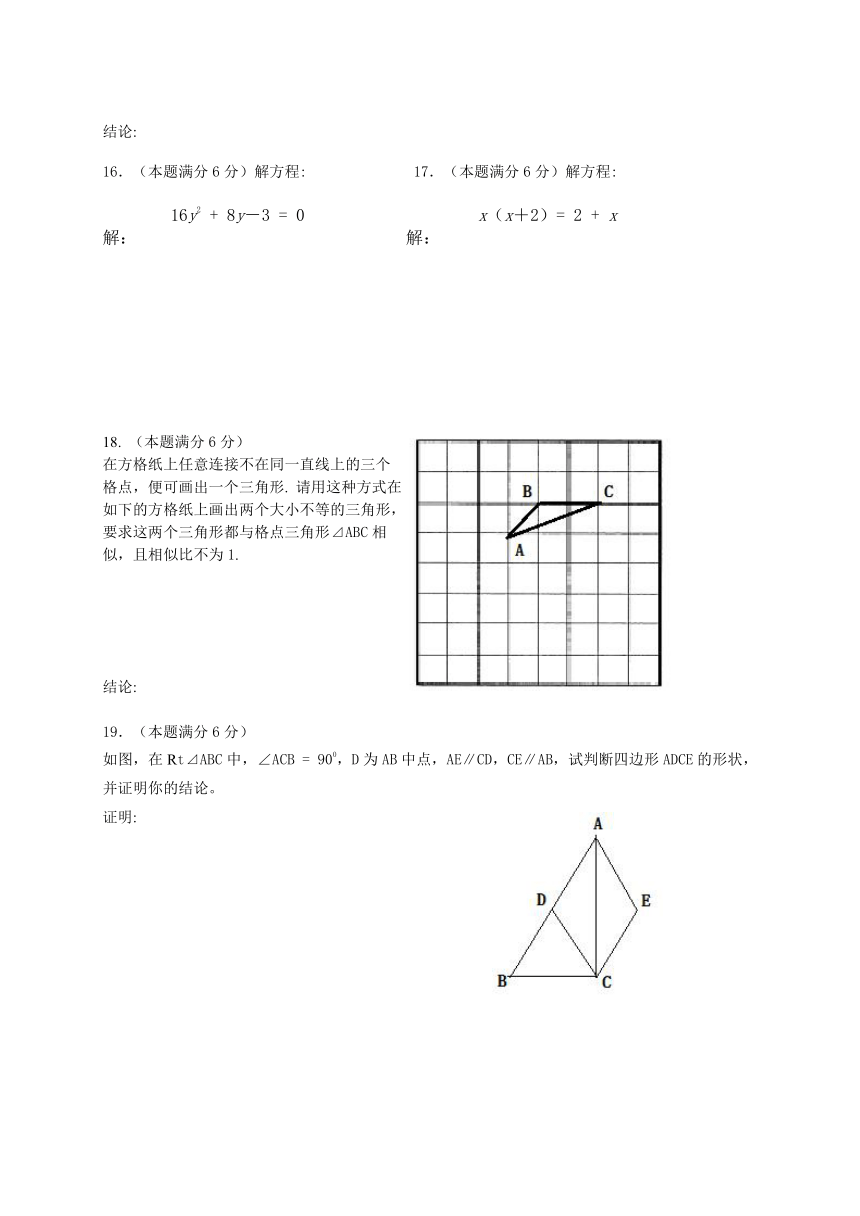
19.(本题满分6分)
如图,在Rt⊿ABC中,∠ACB = 900,D为AB中点,AE∥CD,CE∥AB,试判断四边形ADCE的形状,并证明你的结论。
证明:
20.(本题满分8分)
小颖为学校联欢会设计了一个“ ( http: / / www.21cnjy.com )配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,如果两个转盘分别转出了红色和蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色。
(1)利用画树状图或列表的方法表示游戏所有可能出现的结果;
(2)求游戏者获胜的概率.
解:
21. (本题满分8分)
已知:如图,在△ABC中,AB=AC,AD是 ( http: / / www.21cnjy.com )BC边的中线, AN为△ABC的外角∠CAM的平分线,CE⊥AN于点E,线段DE交AC于点 F.
(1)求证:四边形ADCE为矩形;
(2)线段DF与AB有怎样的关系?证明你的结论.
证明:(1)
(2)
22. 列方程解应用题(本题满分10分)
某商场将进货价为30元的台 ( http: / / www.21cnjy.com )灯以40元售出,平均每月能售出600个,调查表明:售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个,为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时平均每月的销售额是多少元?
解:
23. (本题满分10分)
将两个不全等的直角三角板,Rt△AOB与Rt△DOE叠放在一起,使得两直角∠AOB与
∠DOE的顶点重合, 已知∠OAB=∠ODE=300,下图是直角三角板△DOE绕顶点O顺时针旋转三个瞬间的平面图形..
在旋转过程中,AD:BE的值是否是定值 请利用图①求出这个定值或说明不是定值的理由;
在旋转过程中,AD与BE有什么位置关系 请分别利用图②、图③说明理由.
图① 图② 图③
24. (本题满分12分)
如图,在矩形ABCD中, ( http: / / www.21cnjy.com )AB=12cm,BC=8cm,点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).
(1)是否存在某一时刻t,使得S的值是矩形ABCD面积的 存在,请求出相应的t值;不存在,请说明理由;
(2)若点F在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以F,C,G为顶点的三角形相似?请说明理由
(3) 在点E,F,G出发后,当t = 时, △EFG是直角三角形.
(填空即可,不必说明理由)
学校___________________ 班级_______________ 姓名_________________ 考号__________________
密 封 线
(第24题图)
等级
九年级数学
(考试时间:120分钟;满分:120分)
题号 一 二 三 四 合计
15 16 17 18 19 20 21 22 23 24
得分
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.
2.本试题共有24道题.其中1—8题为选 ( http: / / www.21cnjy.com )择题,请将所选答案的标号填写在第8题后面给出表格的相应位置上;9—14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15—24题请在试题给出的本题位置上做答.
得 分 评卷人 复核人 一、选择题(本题满分24分,共有8道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个 ( http: / / www.21cnjy.com )结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1—8各小题所选答案的标号填写在第8小题后面给出表格的相应位置上.
1. 对于四条线段a、b、c、d,如果ab=cd,那么( ).
A. = B. = C. = D. =
2. 根据下列表格对应值:
1.1 1.2 1.3 1.4
-0.59 0.84 2.29 3.76
判断关于的方程的一个解的范围是( ).
A. 1.1<<1.2 B.1.2<<1.3.
C. 1.3<<1.4 D. 无法判定
3.小明从一定高度随机掷一枚质地均匀的硬币 ( http: / / www.21cnjy.com ),他已经掷了两次硬币,结果都是“正面朝上”,那么,从概率的角度分析,小明第三次掷硬币时, ( ).
A. 一定会正面朝上; B. 正面朝上的可能性大于反面朝上;
C. 反面朝上的可能性大于正面朝上; D. 正、反面朝上的可能性一样大.
4.在平行四边形、菱形、矩形、正方形这四种图形中,既是轴对称图形,也是中心对称图形的有( ).
A.1种 B.2种 C.3种 D.4种
5.用配方法解方程时,配方后所得的方程为( ).
A. ; B.
C. D. .
6.主持人站在舞台的黄金分 ( http: / / www.21cnjy.com )割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是( ).
① AB:AC=AC:BC; ② AC≈6.18米;
③ 米; ④米或米
A.①②③④ B.①②③ C.①③ D.④
7.小亮和小刚按如下规则做游戏:每人从1,2,…,12中任意选择一个数,然后两人各掷一次均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负. 从概率的角度分析,游戏者事先选择( )获胜的可能性较大.
A.5 B.6 C.7 D.8
8. 如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( ).
① 四边形BGDH是菱形; ② AG=1.75;
③ GH=7.5; ④四边形BGDH的面积是37.5.
A.只有①② B.只有②③
C.①②③ D.①②③④ (第8题图)
请将1—8各小题所选答案的标号填写在下表中相应的位置上:
题号 1 2 3 4 5 6 7 8
答案
得 分 评卷人 复核人 二、填空题(本题满分18分,共有6道小题,每小题3分)请将9—14各小题的答案填写在第14小题后面给出表格的相应位置上.
9. 在一个有10万人的小镇,随机调查 ( http: / / www.21cnjy.com )了2 000人,其中有250人看中央电视台的早间新闻,在该镇随便问一人,他看早间新闻的概率大约是______.
10. 如果,那么=______.
11. 某种型号的电视机经过两次降价,价格从原来每台2250元降为每台1440元,设平均每次下降的百分率为,根据题意,可列方程为 .
12. 已知关于x的方程2-4x+m=0的一个根是1-,则它的另一个根是 .
13. 在菱形ABCD中,对角线A ( http: / / www.21cnjy.com )C 、BD相交于点O, BD=6 ,∠ABC =2∠BCD,则对角线AC= .,菱形ABCD面积= .
14.如图,在平行四边形ABCD中, 点F是AD边上一点,连接BF与对角线AC 相交于点E. ①当时, .
②当时, ,
.
请将9—14各小题的答案填写在下表的相应位置上:
题 号 9 10 11
答 案
题 号 12 13 14
答 案
得 分 评卷人 复核人 三、解答题(本题共有10道小题,满分78分)
15.作图题(本题满分6分)
用圆规、直尺作图,不写作法,但要保留作图痕迹.
求作:一个菱形ABCD,使它的对角线AC的长等于已知线段a .
结论:
16.(本题满分6分)解方程: 17.(本题满分6分)解方程:
16y2 + 8y-3 = 0 x(x+2)= 2 + x
解: 解:
18. (本题满分6分)
在方格纸上任意连接不在同一直线上的三个
格点,便可画出一个三角形. 请用这种方式在
如下的方格纸上画出两个大小不等的三角形,
要求这两个三角形都与格点三角形⊿ABC相
似,且相似比不为1.
结论:
19.(本题满分6分)
如图,在Rt⊿ABC中,∠ACB = 900,D为AB中点,AE∥CD,CE∥AB,试判断四边形ADCE的形状,并证明你的结论。
证明:
20.(本题满分8分)
小颖为学校联欢会设计了一个“ ( http: / / www.21cnjy.com )配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,如果两个转盘分别转出了红色和蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色。
(1)利用画树状图或列表的方法表示游戏所有可能出现的结果;
(2)求游戏者获胜的概率.
解:
21. (本题满分8分)
已知:如图,在△ABC中,AB=AC,AD是 ( http: / / www.21cnjy.com )BC边的中线, AN为△ABC的外角∠CAM的平分线,CE⊥AN于点E,线段DE交AC于点 F.
(1)求证:四边形ADCE为矩形;
(2)线段DF与AB有怎样的关系?证明你的结论.
证明:(1)
(2)
22. 列方程解应用题(本题满分10分)
某商场将进货价为30元的台 ( http: / / www.21cnjy.com )灯以40元售出,平均每月能售出600个,调查表明:售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个,为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时平均每月的销售额是多少元?
解:
23. (本题满分10分)
将两个不全等的直角三角板,Rt△AOB与Rt△DOE叠放在一起,使得两直角∠AOB与
∠DOE的顶点重合, 已知∠OAB=∠ODE=300,下图是直角三角板△DOE绕顶点O顺时针旋转三个瞬间的平面图形..
在旋转过程中,AD:BE的值是否是定值 请利用图①求出这个定值或说明不是定值的理由;
在旋转过程中,AD与BE有什么位置关系 请分别利用图②、图③说明理由.
图① 图② 图③
24. (本题满分12分)
如图,在矩形ABCD中, ( http: / / www.21cnjy.com )AB=12cm,BC=8cm,点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).
(1)是否存在某一时刻t,使得S的值是矩形ABCD面积的 存在,请求出相应的t值;不存在,请说明理由;
(2)若点F在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以F,C,G为顶点的三角形相似?请说明理由
(3) 在点E,F,G出发后,当t = 时, △EFG是直角三角形.
(填空即可,不必说明理由)
学校___________________ 班级_______________ 姓名_________________ 考号__________________
密 封 线
(第24题图)
同课章节目录
