山东省菏泽市2022-2023学年高二下学期期末考试数学试卷(含解析)
文档属性
| 名称 | 山东省菏泽市2022-2023学年高二下学期期末考试数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 663.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 00:00:00 | ||
图片预览




文档简介
山东省菏泽市2022-2023学年高二下学期期末考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、有一次考试的选做题部分,要求在第1题的4个小题中选做3个小题,在第2题的3个小题中选做2个小题,在第3题的2个小题中选做1个小题,不同的选法种数是( )
A.9 B.24 C.84 D.288
2、如图,函数的图象在点处的切线是l,则( )
A.1 B.2 C.0 D.-1
3、有两箱零件,第一箱内有10件,其中有2件次品;第二箱内有20件,其中有3件次品.现从两箱中随意挑选一箱,然后从该箱中随机取1个零件,则取出的零件是次品的概率是( )
A. B. C. D.
4、甲、乙两类水果的质量(单位:)分别服从正态分布,,其相应的分布密度曲线如图所示,则下列说法正确的是( )
A.甲类水果的平均质量比乙类水果的平均质量大
B.乙类水果的质量比甲类水果的质量更集中于均值左右
C.水果的质量服从的正态分布的参数
D.甲类水果的平均质量
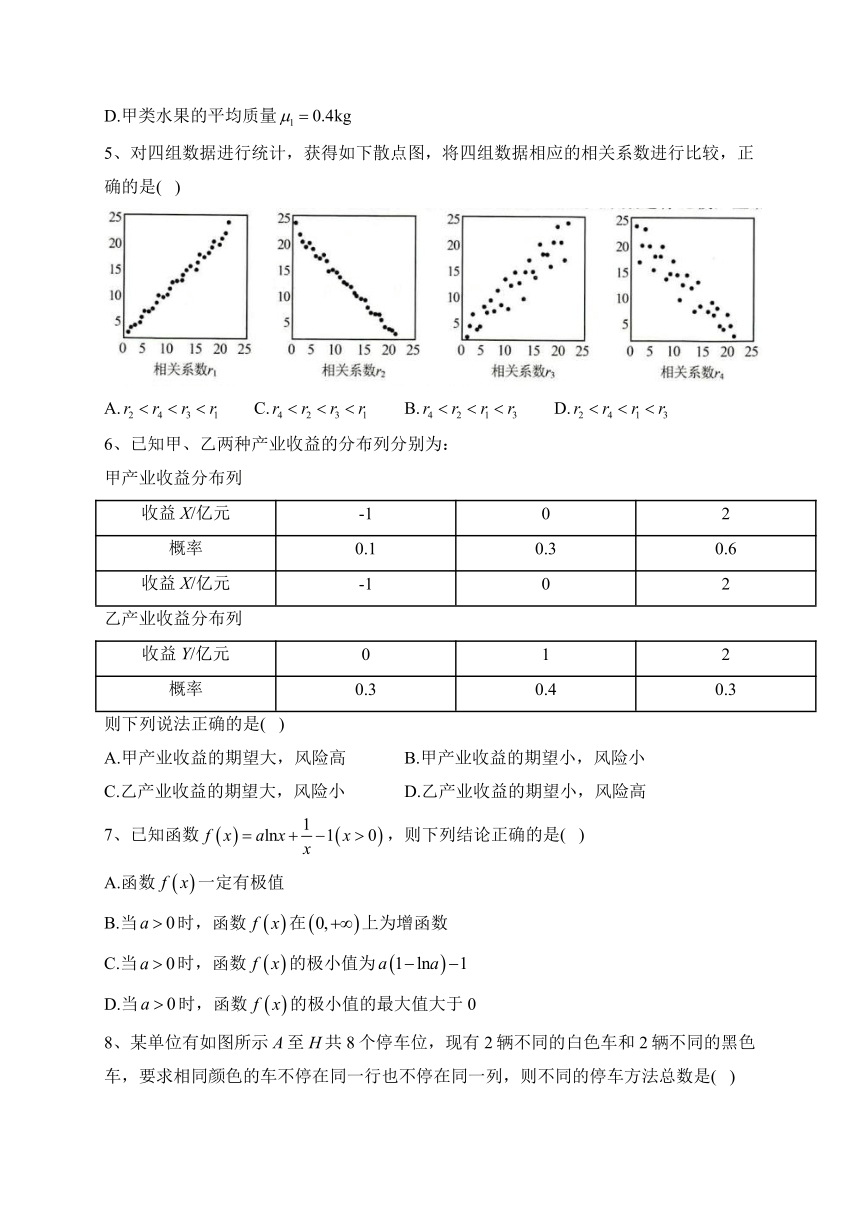
5、对四组数据进行统计,获得如下散点图,将四组数据相应的相关系数进行比较,正确的是( )
A. C. B. D.
6、已知甲、乙两种产业收益的分布列分别为:
甲产业收益分布列
收益X/亿元 -1 0 2
概率 0.1 0.3 0.6
收益X/亿元 -1 0 2
乙产业收益分布列
收益Y/亿元 0 1 2
概率 0.3 0.4 0.3
则下列说法正确的是( )
A.甲产业收益的期望大,风险高 B.甲产业收益的期望小,风险小
C.乙产业收益的期望大,风险小 D.乙产业收益的期望小,风险高
7、已知函数,则下列结论正确的是( )
A.函数一定有极值
B.当时,函数在上为增函数
C.当时,函数的极小值为
D.当时,函数的极小值的最大值大于0
8、某单位有如图所示A至H共8个停车位,现有2辆不同的白色车和2辆不同的黑色车,要求相同颜色的车不停在同一行也不停在同一列,则不同的停车方法总数是( )
A B C D
E F G H
A.288 B.336 C.576 D.1680
二、多项选择题
9、千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化、总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”,某同学甲为了验证“日落云里走,雨在半夜后”,观察了地区A的100天日落和夜晩天气,得到如下表格(单位:天)
夜晚天气 日落云里走 下雨 未下雨
出现 25 5
未出现 25 45
临界值参照表:参考公式:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
经计算得到.则甲同学对地区A天气的下列判断正确的有( )
A.夜晩下雨的概率约为
B.末出现“日落云里走”,夜晩下雨的概率约为
C.有99%的把握判断“日落云里”是否出现”与“夜晩下雨”有关
D.出现“日落云里走”,有99%的把握判断夜晩会下雨
10、在的展开式中,下列结论正确的有( )
A.二项式系数的和为 B.各项系数的和为
C.奇数项系数的和为 D.二项式系数最大的项为
11、已知函数的导函数的图象如图所示.则下列结论正确的有( )
A. B.函数在上是减函数
C.函数在上无极值 D.函数在上有极值
12、对于1,2…,,的全部排列,定义Euler数(其中,,1,,n)表示其中恰有k次升高的排列的个数(注:k次升高是指在排列中有k处,,,).例如:1,2,3的排列共有:123,132,213,231,312,321六个,恰有1处升高的排列有如下四个:132,213,231,312,因此:.则下列结论正确的有( )
A. B.
C. D.
三、填空题
13、根据下面的数据:
x 1 2 3 4
y 31.6 52.5 72 91.9
求得y关于x的回归直线方程为,则这组数据相对于所求的回归直线方程的4个残差的方差为_____________.
14、的展开式中的系数为______.
15、某班一天上午有4节课,下午有2节课,现要安排该班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表,要求数学不排在下午,体育不排在上午第一、二节和下午第一节,艺术不排在上午,不同排法种数为______(用数字作答).
16、已知函数有唯一零点,则__________.
四、解答题
17、已知函数.
(1)求的导数;
(2)求的图象在处的切线方程.
18、已知随机变量X的分布列为:
X 5 6 7 8 9
P 0.1 a 0.2 b 0.3
(1)若,求a、b的值;
(2)记事件;事件为偶数.已知,求a,b的值.
19、电商的兴起,促进了我市经济的发展.已知某电商平台对其牌下一家专营店在2022年3月至7月的营业收入y(单位:万元)进行统计,得到以下数据:
月份x 3 4 5 6 7
营业收入y 10 12 11 12 20
(1)依据表中给出的数据,用样本相关系数说明营业收入y与月份x的相关程度;
(2)试用最小二乘法求出营业收入与月份的一元线性回归方程,并预测当时该专营店的营业收入.
(,)
,.以上各式仅供参考)
20、已知函数.
(1)求函数的单调区间;
(2)求函数的极值;
(3)若函数在上的最小值是,求实数a的取值范围.
21、贵州榕江(三宝侗寨)和美乡村足球超级联赛,简称“村超”,该活动在榕江县如火如荼的进行中,这项活动大大促进了当地村民参加体育活动的积极性.为了更好的提高全民素质,某镇建议成人每周进行5.5小时至8小时的运动.已知“A村”有56%的居民每周运动总时间超过8小时,“B村”有65%的居民每周运动总时间超过8小时,“C村”有70%的居民每周运动总时间超过8小时,且A,B,C三个村的居民人数之比为.
(1)从这三个村中随机抽取1名居民,求该居民每周运动总时间超过8小时的概率;
(2)假设这三个村每名居民每周运动总时间为随机变量X(单位:小时),且.
现从这三个村中随机抽取3名居民,求至少有两名居民每周运动总时间为8至9小时的概率.
22、已知(e为自然对数的底数)在处的切线方程为.
(1)求的解析式;
(2)若,对,任意成立,求ab最大值.
参考答案
1、答案:B
解析:由题,在一次考试的选做题部分可分三步,则.故选:B.
2、答案:C
解析:由图象可得切线过点,所以 切线l的方程为 ,即 ,
所以切线的斜率为-1,所以 因为点在切线上,
所以, 所以 ,所以,
故选: C.
3、答案:C
解析:
4、答案:D
解析:
5、答案:A
解析:
6、答案:A
解析:由题意可得
,
,
,
,
故 ,即甲产业收益的期望大,风险高,
故选:A
7、答案:C
解析:
8、答案:B
解析:第一步: 排白车, 第一行选一个位置, 则第二行有三个位置可选, 由于车是不相同 的, 故白车的停法有 (种). 第二 步: 排黑车, 若白车选AF, 则黑车有BE,BG,BH,CE,CH,DE,DG 共 7 种选择, 黑车是不相同的,故黑车的停法有 (种).根据分步计数原理,共有 (种)
9、答案:ABC
解析:对于A, 根据列联表, 100 天中有 50 天下雨, 50 天末下雨, 所以夜晩下雨的概率约为 , 故 A 正确;
对于 B, 末出现 “日落云里走” 夜晩下雨的有 25 天, 末出现 “日落云里走” 的一共 天, 所以 末出现 “日落云里走” 夜晩下雨的概率约为, 故 B 正确;
对于C, 由题意可知 , 因此依据 的独立性检验, 认为 “日落云里走” 是否出 现与夜晩天气有关, 故 C 正确,
对于D, 由选项 C 知, 有关只是说可能性, 不代表一定下雨, 故 D 错误.
故选: ABC.
10、答案:ACD
解析:
11、答案:ACD
解析:由函数的导函数 的图象可 知,
当时, , 即 在 上单调递减,故 ,A正确;
当时,, 即 在 上单调递增,
当时, , 即 在 上单调递减,
故函数 在 上不是减函数,B 错误;
当 时,,在 上单调递增,
故函数 在 上无极值,C正确;
当 时,, 即 在 上单调递减,
当 时, ,即在 上单调递增,
故为函数的极小值点,即函数在上有极值,D正确,
故选: ACD
12、答案:BC
解析:
13、答案:0.105
解析:根据 ,分别将,2,3,4
代入求得分别为:32,52,72,92,
则 4 个残差为-0.4,0.5,0,-0.1,残差的平均数为0,故残差的方差为
故答案为:0.105
14、答案:135
解析:,
的通项公式为,
,1,2,,9,
的展开式中项的系数为
x项的系数为
的展开式中的系数为.
15、答案:96
解析:可分体育排在下午和上午两类情况:
①若体育排在上午: 先排体育,有2种方法,后排数学,有3种方法,再排艺术,有 2 种方法,最后再排其它3科,有种方法,故体育排在上午的不同排法种数为,
②若体育排在下午:先排体育,有 1 种方 法,后排艺术,有 1 种方法,最后再排其它 4 科,有种方法, 故体育排在下午的不同排法种数为 ; 故不同排法种数为.
故答案为:96.
16、答案:
解析:由题意可得,
,
即 ,
构造函数 ,其中 ,
则,所以在上单调递增,
由可得,
,所以,
所以.
故答案为:
17、答案:(1)
(2)
解析:(1)由
(2)由,所以,所以的图象在处的切线方程为,即
18、答案: (1),
(2),
解析:(1)由随机变量分布列的性质,有,得,①
又
②
由①和②,解得,.
(2)由事件,
得;
又事件为偶数,得;
所以,得;
由(1)知,所以;
所以,
19、答案:(1)因为,说明y与x的正线性相关性较强
(2)
解析:(1)由已知求得:,,,
,;
,
因为,说明y与x的正线性相关性较强;
(2)由条件和(1)中数据,可得,,
则y关于x的线性回归方程为.
当时,,由此可预测该专营店在时的营业收入为19万元.--12分
20、答案:(1)的单调增减区间为和,单调递递区间为
(2)极大值为,极小值为
(3)
解析:(1)函数 的定义域为R,,
令,得,当或时,;当时,.
所以的单调增减区间为和,单调递递区间为;
(2)由(1)知的单调递增区间为,单调递减区间为,
所以的极大值为,极小值为.
(3)由函数在上的最小值是,可知,
由,可知是方程的一个解,
所以,或;
由的单调增减区间为和,单调递递区间为可知要使,使即可.
所以实数a的取值范围是.
21、答案:(1)0.65
(2)0.216
解析:(1)因为A,B,C三个村的居民人数之比为,可设A,B,C三个村的居民人数为,,,
所以A村每周运动总时间超过8小时的人数为:,
B村每周运动总时间超过 8小时的人数为:,
C村每周运动总时间超过8小时的人 数为:,
该居民每周运动总时间超过小时的概率;
(2)因为这三个村每名居民每周运动总时间为随机变量X(单位:小时),满足,
所以,
由(1)知,,所以,
因为,所以,
所以从这三个村中随机抽取3名居民,至少有两名居民每周运动总时间为8至9小时的概率为:.
22、答案:(1)
(2)见解析
解析:(1)由,得,,所以,
所以;
(2)令,
则.
易知单调递增,当时,;
当时,;
所以存在唯一零点,记为,即 ,①
当时,,单调递减;
当时,,单调递增;
所以,
结合①得:,
所以,得:或
当时,,得;
当时,,得,矛盾.
故,所以,当且仅当取到最大值.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、有一次考试的选做题部分,要求在第1题的4个小题中选做3个小题,在第2题的3个小题中选做2个小题,在第3题的2个小题中选做1个小题,不同的选法种数是( )
A.9 B.24 C.84 D.288
2、如图,函数的图象在点处的切线是l,则( )
A.1 B.2 C.0 D.-1
3、有两箱零件,第一箱内有10件,其中有2件次品;第二箱内有20件,其中有3件次品.现从两箱中随意挑选一箱,然后从该箱中随机取1个零件,则取出的零件是次品的概率是( )
A. B. C. D.
4、甲、乙两类水果的质量(单位:)分别服从正态分布,,其相应的分布密度曲线如图所示,则下列说法正确的是( )
A.甲类水果的平均质量比乙类水果的平均质量大
B.乙类水果的质量比甲类水果的质量更集中于均值左右
C.水果的质量服从的正态分布的参数
D.甲类水果的平均质量
5、对四组数据进行统计,获得如下散点图,将四组数据相应的相关系数进行比较,正确的是( )
A. C. B. D.
6、已知甲、乙两种产业收益的分布列分别为:
甲产业收益分布列
收益X/亿元 -1 0 2
概率 0.1 0.3 0.6
收益X/亿元 -1 0 2
乙产业收益分布列
收益Y/亿元 0 1 2
概率 0.3 0.4 0.3
则下列说法正确的是( )
A.甲产业收益的期望大,风险高 B.甲产业收益的期望小,风险小
C.乙产业收益的期望大,风险小 D.乙产业收益的期望小,风险高
7、已知函数,则下列结论正确的是( )
A.函数一定有极值
B.当时,函数在上为增函数
C.当时,函数的极小值为
D.当时,函数的极小值的最大值大于0
8、某单位有如图所示A至H共8个停车位,现有2辆不同的白色车和2辆不同的黑色车,要求相同颜色的车不停在同一行也不停在同一列,则不同的停车方法总数是( )
A B C D
E F G H
A.288 B.336 C.576 D.1680
二、多项选择题
9、千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化、总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”,某同学甲为了验证“日落云里走,雨在半夜后”,观察了地区A的100天日落和夜晩天气,得到如下表格(单位:天)
夜晚天气 日落云里走 下雨 未下雨
出现 25 5
未出现 25 45
临界值参照表:参考公式:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
经计算得到.则甲同学对地区A天气的下列判断正确的有( )
A.夜晩下雨的概率约为
B.末出现“日落云里走”,夜晩下雨的概率约为
C.有99%的把握判断“日落云里”是否出现”与“夜晩下雨”有关
D.出现“日落云里走”,有99%的把握判断夜晩会下雨
10、在的展开式中,下列结论正确的有( )
A.二项式系数的和为 B.各项系数的和为
C.奇数项系数的和为 D.二项式系数最大的项为
11、已知函数的导函数的图象如图所示.则下列结论正确的有( )
A. B.函数在上是减函数
C.函数在上无极值 D.函数在上有极值
12、对于1,2…,,的全部排列,定义Euler数(其中,,1,,n)表示其中恰有k次升高的排列的个数(注:k次升高是指在排列中有k处,,,).例如:1,2,3的排列共有:123,132,213,231,312,321六个,恰有1处升高的排列有如下四个:132,213,231,312,因此:.则下列结论正确的有( )
A. B.
C. D.
三、填空题
13、根据下面的数据:
x 1 2 3 4
y 31.6 52.5 72 91.9
求得y关于x的回归直线方程为,则这组数据相对于所求的回归直线方程的4个残差的方差为_____________.
14、的展开式中的系数为______.
15、某班一天上午有4节课,下午有2节课,现要安排该班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表,要求数学不排在下午,体育不排在上午第一、二节和下午第一节,艺术不排在上午,不同排法种数为______(用数字作答).
16、已知函数有唯一零点,则__________.
四、解答题
17、已知函数.
(1)求的导数;
(2)求的图象在处的切线方程.
18、已知随机变量X的分布列为:
X 5 6 7 8 9
P 0.1 a 0.2 b 0.3
(1)若,求a、b的值;
(2)记事件;事件为偶数.已知,求a,b的值.
19、电商的兴起,促进了我市经济的发展.已知某电商平台对其牌下一家专营店在2022年3月至7月的营业收入y(单位:万元)进行统计,得到以下数据:
月份x 3 4 5 6 7
营业收入y 10 12 11 12 20
(1)依据表中给出的数据,用样本相关系数说明营业收入y与月份x的相关程度;
(2)试用最小二乘法求出营业收入与月份的一元线性回归方程,并预测当时该专营店的营业收入.
(,)
,.以上各式仅供参考)
20、已知函数.
(1)求函数的单调区间;
(2)求函数的极值;
(3)若函数在上的最小值是,求实数a的取值范围.
21、贵州榕江(三宝侗寨)和美乡村足球超级联赛,简称“村超”,该活动在榕江县如火如荼的进行中,这项活动大大促进了当地村民参加体育活动的积极性.为了更好的提高全民素质,某镇建议成人每周进行5.5小时至8小时的运动.已知“A村”有56%的居民每周运动总时间超过8小时,“B村”有65%的居民每周运动总时间超过8小时,“C村”有70%的居民每周运动总时间超过8小时,且A,B,C三个村的居民人数之比为.
(1)从这三个村中随机抽取1名居民,求该居民每周运动总时间超过8小时的概率;
(2)假设这三个村每名居民每周运动总时间为随机变量X(单位:小时),且.
现从这三个村中随机抽取3名居民,求至少有两名居民每周运动总时间为8至9小时的概率.
22、已知(e为自然对数的底数)在处的切线方程为.
(1)求的解析式;
(2)若,对,任意成立,求ab最大值.
参考答案
1、答案:B
解析:由题,在一次考试的选做题部分可分三步,则.故选:B.
2、答案:C
解析:由图象可得切线过点,所以 切线l的方程为 ,即 ,
所以切线的斜率为-1,所以 因为点在切线上,
所以, 所以 ,所以,
故选: C.
3、答案:C
解析:
4、答案:D
解析:
5、答案:A
解析:
6、答案:A
解析:由题意可得
,
,
,
,
故 ,即甲产业收益的期望大,风险高,
故选:A
7、答案:C
解析:
8、答案:B
解析:第一步: 排白车, 第一行选一个位置, 则第二行有三个位置可选, 由于车是不相同 的, 故白车的停法有 (种). 第二 步: 排黑车, 若白车选AF, 则黑车有BE,BG,BH,CE,CH,DE,DG 共 7 种选择, 黑车是不相同的,故黑车的停法有 (种).根据分步计数原理,共有 (种)
9、答案:ABC
解析:对于A, 根据列联表, 100 天中有 50 天下雨, 50 天末下雨, 所以夜晩下雨的概率约为 , 故 A 正确;
对于 B, 末出现 “日落云里走” 夜晩下雨的有 25 天, 末出现 “日落云里走” 的一共 天, 所以 末出现 “日落云里走” 夜晩下雨的概率约为, 故 B 正确;
对于C, 由题意可知 , 因此依据 的独立性检验, 认为 “日落云里走” 是否出 现与夜晩天气有关, 故 C 正确,
对于D, 由选项 C 知, 有关只是说可能性, 不代表一定下雨, 故 D 错误.
故选: ABC.
10、答案:ACD
解析:
11、答案:ACD
解析:由函数的导函数 的图象可 知,
当时, , 即 在 上单调递减,故 ,A正确;
当时,, 即 在 上单调递增,
当时, , 即 在 上单调递减,
故函数 在 上不是减函数,B 错误;
当 时,,在 上单调递增,
故函数 在 上无极值,C正确;
当 时,, 即 在 上单调递减,
当 时, ,即在 上单调递增,
故为函数的极小值点,即函数在上有极值,D正确,
故选: ACD
12、答案:BC
解析:
13、答案:0.105
解析:根据 ,分别将,2,3,4
代入求得分别为:32,52,72,92,
则 4 个残差为-0.4,0.5,0,-0.1,残差的平均数为0,故残差的方差为
故答案为:0.105
14、答案:135
解析:,
的通项公式为,
,1,2,,9,
的展开式中项的系数为
x项的系数为
的展开式中的系数为.
15、答案:96
解析:可分体育排在下午和上午两类情况:
①若体育排在上午: 先排体育,有2种方法,后排数学,有3种方法,再排艺术,有 2 种方法,最后再排其它3科,有种方法,故体育排在上午的不同排法种数为,
②若体育排在下午:先排体育,有 1 种方 法,后排艺术,有 1 种方法,最后再排其它 4 科,有种方法, 故体育排在下午的不同排法种数为 ; 故不同排法种数为.
故答案为:96.
16、答案:
解析:由题意可得,
,
即 ,
构造函数 ,其中 ,
则,所以在上单调递增,
由可得,
,所以,
所以.
故答案为:
17、答案:(1)
(2)
解析:(1)由
(2)由,所以,所以的图象在处的切线方程为,即
18、答案: (1),
(2),
解析:(1)由随机变量分布列的性质,有,得,①
又
②
由①和②,解得,.
(2)由事件,
得;
又事件为偶数,得;
所以,得;
由(1)知,所以;
所以,
19、答案:(1)因为,说明y与x的正线性相关性较强
(2)
解析:(1)由已知求得:,,,
,;
,
因为,说明y与x的正线性相关性较强;
(2)由条件和(1)中数据,可得,,
则y关于x的线性回归方程为.
当时,,由此可预测该专营店在时的营业收入为19万元.--12分
20、答案:(1)的单调增减区间为和,单调递递区间为
(2)极大值为,极小值为
(3)
解析:(1)函数 的定义域为R,,
令,得,当或时,;当时,.
所以的单调增减区间为和,单调递递区间为;
(2)由(1)知的单调递增区间为,单调递减区间为,
所以的极大值为,极小值为.
(3)由函数在上的最小值是,可知,
由,可知是方程的一个解,
所以,或;
由的单调增减区间为和,单调递递区间为可知要使,使即可.
所以实数a的取值范围是.
21、答案:(1)0.65
(2)0.216
解析:(1)因为A,B,C三个村的居民人数之比为,可设A,B,C三个村的居民人数为,,,
所以A村每周运动总时间超过8小时的人数为:,
B村每周运动总时间超过 8小时的人数为:,
C村每周运动总时间超过8小时的人 数为:,
该居民每周运动总时间超过小时的概率;
(2)因为这三个村每名居民每周运动总时间为随机变量X(单位:小时),满足,
所以,
由(1)知,,所以,
因为,所以,
所以从这三个村中随机抽取3名居民,至少有两名居民每周运动总时间为8至9小时的概率为:.
22、答案:(1)
(2)见解析
解析:(1)由,得,,所以,
所以;
(2)令,
则.
易知单调递增,当时,;
当时,;
所以存在唯一零点,记为,即 ,①
当时,,单调递减;
当时,,单调递增;
所以,
结合①得:,
所以,得:或
当时,,得;
当时,,得,矛盾.
故,所以,当且仅当取到最大值.
同课章节目录
