相似判定(2)[下学期]

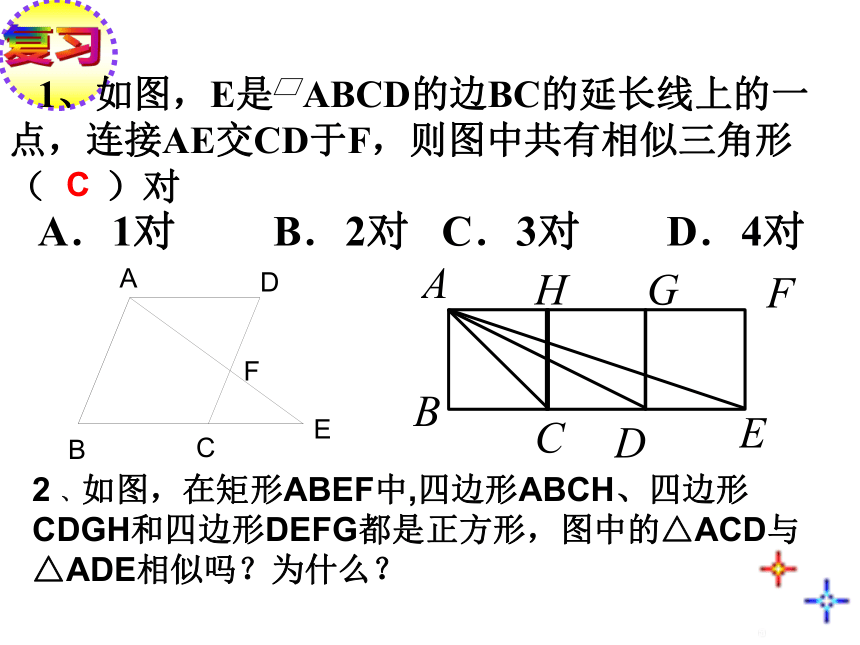
课件10张PPT。1、如图，E是 ABCD的边BC的延长线上的一点，连接AE交CD于F，则图中共有相似三角形（ ）对
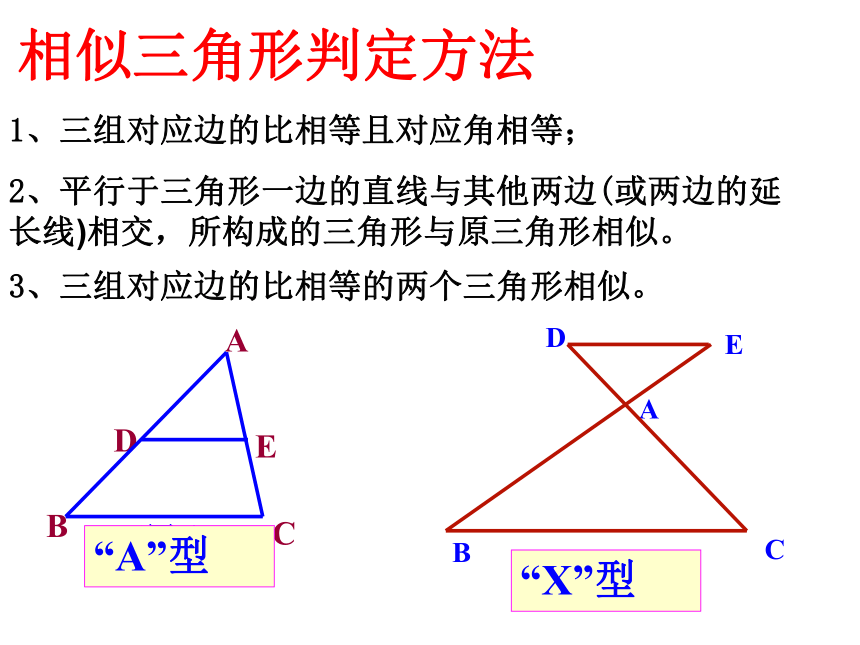
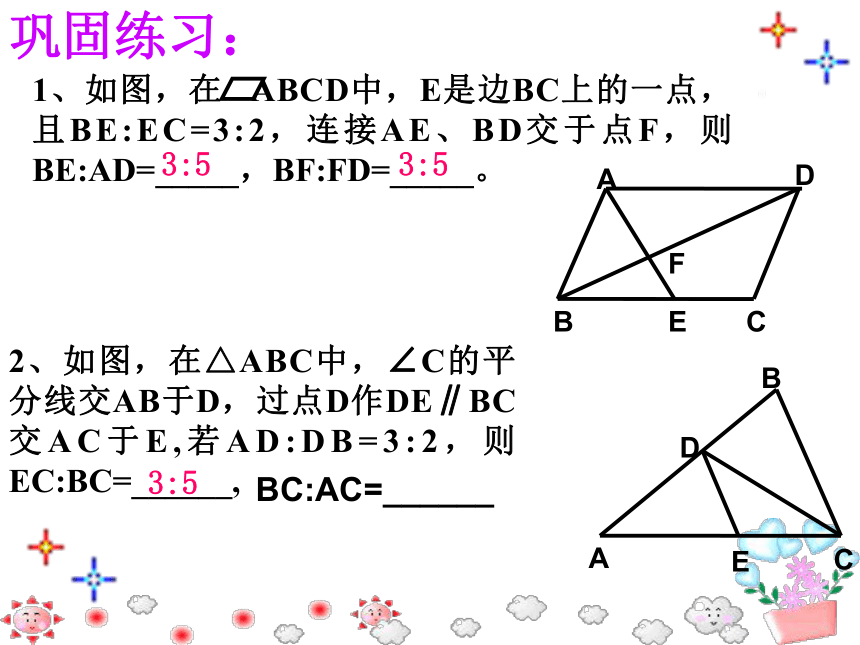
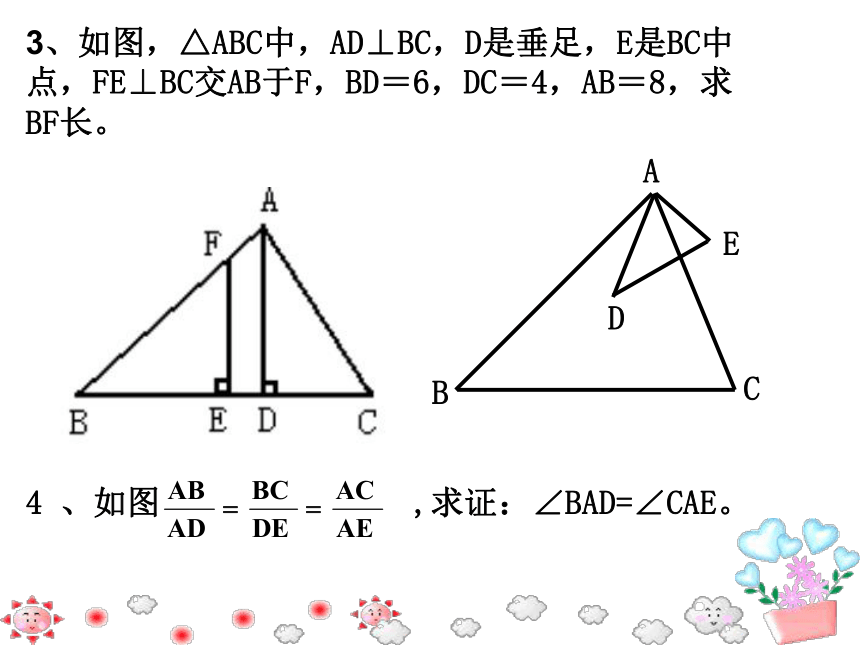
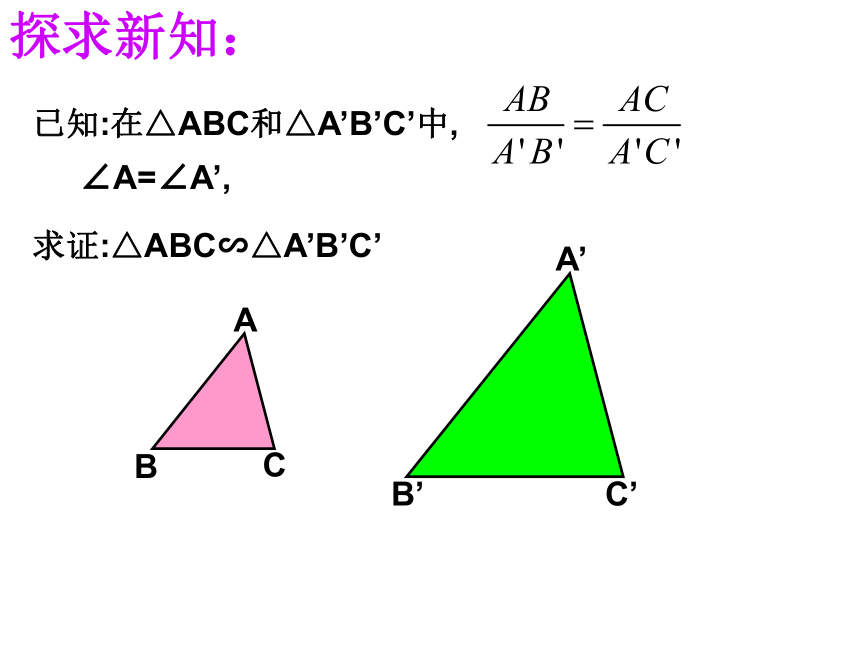
A．1对 B．2对 C．3对 D．4对C2 、如图，在矩形ABEF中,四边形ABCH、四边形CDGH和四边形DEFG都是正方形，图中的△ACD与△ADE相似吗？为什么？相似三角形判定方法1、三组对应边的比相等且对应角相等；3、三组对应边的比相等的两个三角形相似。2、平行于三角形一边的直线与其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似。1、如图，在 ABCD中，E是边BC上的一点，且BE:EC=3:2，连接AE、BD交于点F，则BE:AD=_____，BF:FD=_____。2、如图，在△ABC中，∠C的平分线交AB于D，过点D作DE∥BC交AC于E,若AD:DB=3:2，则EC:BC=______,3:53:53:5巩固练习：BC:AC=______3、如图，△ABC中，AD⊥BC，D是垂足，E是BC中点，FE⊥BC交AB于F，BD＝6，DC＝4，AB＝8，求BF长。 4 、如图 ,求证：∠BAD=∠CAE。已知:在△ABC和△A’B’C’中,∠A=∠A’,求证:△ABC∽△A’B’C’探求新知：判定定理2：如果两个三角形的两组对应边的比相等，并且相应的夹角相等,那么这两个三角形相似。结 论可以简单说成：两边对应成比例且夹角相等，两三角形相似。在△ABC和△A’B’C’中,∴△ABC∽△A’B’C’∠A=∠A’,根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.∠A=120O,AB=7,AC=14
∠A’=120O,A’B’=3,A’C’=6
(3)CA’XAC=BCXCB’（2）∠B＝1200，AB=2cm，AC=6cm，
∠B’＝1200，A’B’= 8cm，A’C’=24cm（2）∠A＝1200，AB=2cm，AC=6cm，
∠B’＝1200，B’C’= 8cm，A’B’=24cm例１：如图，在△ABC中，D在AB上，已知AD=2 cm，AC=4cm，AB=8cm，求证：△ACD∽△ABC.变式：如图，D是△ ABC的边AB上的一点，要使△ ACD ∽△ABC?则它们还必须具备的条件是（　　）巩固练习：1、如图，在△ABC中，已知AD=2 ，BD=4，AE=3，EC=1,则下列结论正确的是＿＿＿＿＿＿＿＿△AED∽△ABC
DE= BC
∠ADE=∠C
若∠E=60O,则∠C=60O巩固练习：3、在△ABC中，已知AB=9cm，AC=6cm， D在AB上， 且AD=6cm， E在直线AC上，若△ABC与以A、D、E为顶点的三角形相似，求AE的值。