八年级数学上册试题 12.2 用待定系数法求函数解析式-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 12.2 用待定系数法求函数解析式-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 339.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 23:21:37 | ||
图片预览




文档简介
12.2 用待定系数法求函数解析式
一、单选题
1.以下四点:(1,2),(2,3),(0,1),(﹣2,3)在直线y=2x+1上的有( )
A.1个 B.2个 C.3个 D.4个
2.为了改善生态环境,政府决定绿化荒地,计划第一年先植树万亩,以后每年都植树万亩,则植树的总面积(万亩)与时间(年)的函数关系式是( )
A. B.
C. D.
3.把经过点(-1,1)和(1,3)的直线向右移动2个单位后过点(3,a),则a的值为( )
A.1 B.2 C.3 D.4
4.若一次函数y=2x+b的图象经过A(-1,3)则b的值为( )
A.2 B.3 C.4 D.5
5.一次函数关于轴对称的图象经过,则的值是( )
A.1 B.-1 C.5 D.-5
6.已知直线与两坐标轴所围成的三角形面积等于4,则直线的解析式为( )
A. B. C. D.或
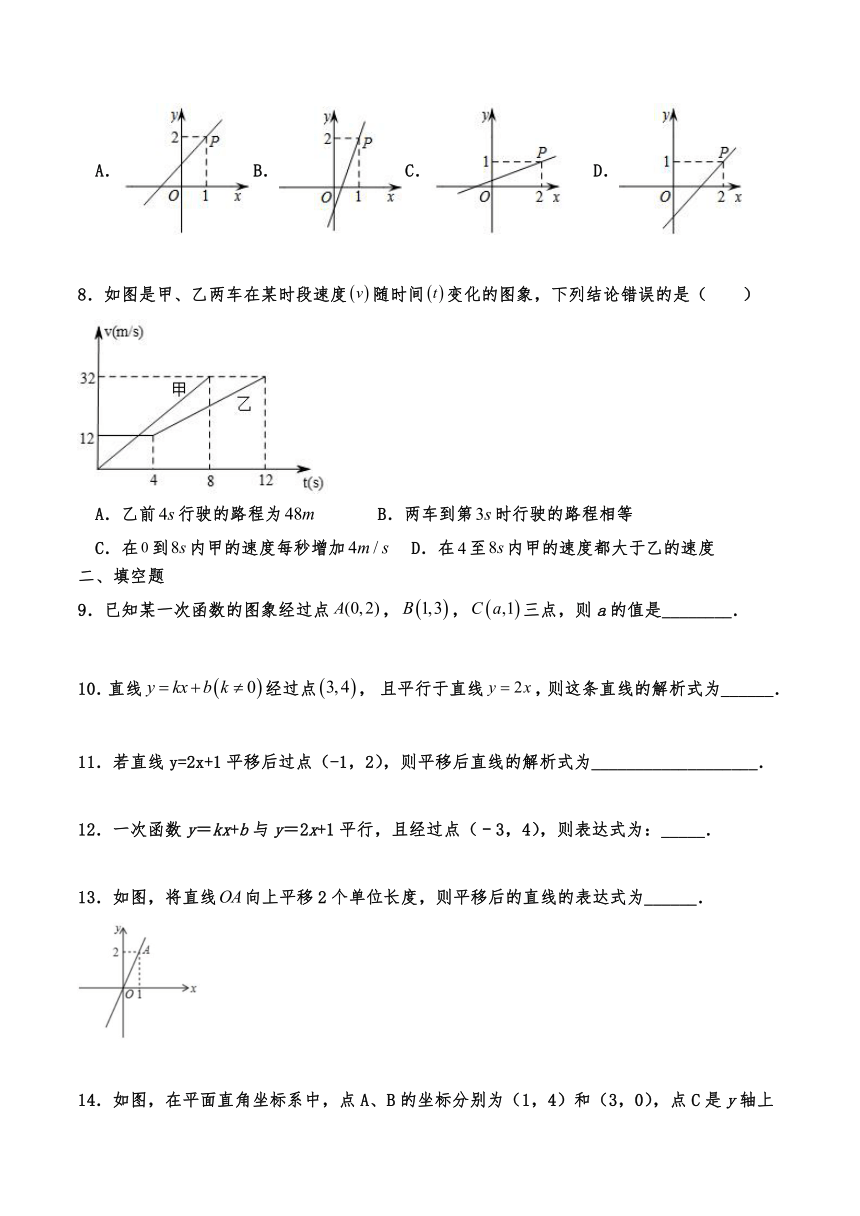
7.在平面直角坐标系中,己知函数的图象过点,则该函数的图象可能是( )
A.B.C. D.
8.如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前行驶的路程为 B.两车到第时行驶的路程相等
C.在到内甲的速度每秒增加 D.在至内甲的速度都大于乙的速度
二、填空题
9.已知某一次函数的图象经过点,,三点,则a的值是________.
10.直线经过点, 且平行于直线,则这条直线的解析式为______.
11.若直线y=2x+1平移后过点(-1,2),则平移后直线的解析式为___________________.
12.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
13.如图,将直线向上平移2个单位长度,则平移后的直线的表达式为______.
14.如图,在平面直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,△BOC的面积为_________.
三、解答题
15.已知是关于的一次函数,且当时,;当时,.
(1)求关于的函数表达式
(2)若一次函数的图象与轴、轴分别交于两点, 求的面积.
16.已知是的一次函数,且当时,的值是9;当 时,的值是-3.
(1)求关于的函数关系式;
(2)当时,求的取值范围.
17.已知一次函数的图象经过点和点,且点B在正比例函数的图象上.
(1)求a的值;
(2)求一次函数的解析式;
(3)若,是这个一次函数图象上的两点,试比较与的大小.
18.已知一次函数经过点,O为坐标原点.
(1)求的值;
(2)当函数值时,求的取值范围.
19.已知一次函数的图象与轴交点在轴上方,且随的增大而减小,为整数.
(1)求的值;
(2)写出此一次函数的表达式,并画出函数图象;
(3)若点为此一次函数图象上一点,点是图象与轴交点,且的面积为,求点的坐标.
20.如图,点的坐标为,点在直线上运动.
(1)若点的坐标是,把直线向上平移个单位后,与直线的交点在第一象限,求的取值范围.
(2)当线段最短时,求点的坐标.
答案
一、单选题
A.B.C.D.D.D.D.B.
二、填空题
9. 1.
10.y=2x-2.
11.
12.y=2x+10.
13..
14.4.5.
三、解答题
15.
(1)∵一次函数y=kx+b(k≠0)的图象过点(1,-4),(2,-6).
∴,解得:.
∴这个一次函数的解析式为:y=-2x-2;
(2)令y=0,则x=-1,
∴A( 1,0),OA=1
令x=0,则y=-2,
∴B(0,-2),OB=2
∴S△OAB=OA OB=×1×2=1.
16.
(1)设y=kx+b(k≠0),
得 ,
解得: ,
y=-2x+1,
(2) y=-2x+1,
,
,
,
,
,
,
17.
(1)∵点B(-a,3)在正比例函数y=-3x的图象上,
∴3=-3×(-a),
∴a=1;
(2)由(1)可得点B的坐标为(-1,3),将(-1,3)和(0,2)代入y=kx+b中,
得b=2,代入-k+b=3,解得k=-1,∴一次函数的解析式为y=-x+2;
(3)∵-1<0,∴y随x的增大而减小.
又∵m>m-1,∴y1<y2.
18.
解:(1)把代入中,得,解得;
(2)当时,,解得.
19.
解:(1)∵一次函数的图象与轴交点在轴上方,且随的增大而减小
∴
∴
∵为整数
∴.
(2)∵
∴一次函数的解析式为
∵当时,;当时,
∴函数图像经过、
∴在平面直角坐标系中描出、,再过这两个点做直线
∴可画出一次函数的图象,如图:
.
(3)∵点为一次函数图象上一点
∴设点的坐标为
∵点是图象与轴交点
∴
∴
∵
∴
∴
∴
∴当时,;当时,
∴点的坐标为或,如图
.
20.
(1)设直线的解析式为.
点的坐标为,点的坐标是,
,
解得,
直线的解析式为,
把直线向上平移个单位后得.
由,解得,
即交点为.
由题意,得,
解得;
(2)最短时有,设此时直线的解析式为,将代入,得,解得,
即直线的解析式为,
由,解得,
点坐标为.
一、单选题
1.以下四点:(1,2),(2,3),(0,1),(﹣2,3)在直线y=2x+1上的有( )
A.1个 B.2个 C.3个 D.4个
2.为了改善生态环境,政府决定绿化荒地,计划第一年先植树万亩,以后每年都植树万亩,则植树的总面积(万亩)与时间(年)的函数关系式是( )
A. B.
C. D.
3.把经过点(-1,1)和(1,3)的直线向右移动2个单位后过点(3,a),则a的值为( )
A.1 B.2 C.3 D.4
4.若一次函数y=2x+b的图象经过A(-1,3)则b的值为( )
A.2 B.3 C.4 D.5
5.一次函数关于轴对称的图象经过,则的值是( )
A.1 B.-1 C.5 D.-5
6.已知直线与两坐标轴所围成的三角形面积等于4,则直线的解析式为( )
A. B. C. D.或
7.在平面直角坐标系中,己知函数的图象过点,则该函数的图象可能是( )
A.B.C. D.
8.如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前行驶的路程为 B.两车到第时行驶的路程相等
C.在到内甲的速度每秒增加 D.在至内甲的速度都大于乙的速度
二、填空题
9.已知某一次函数的图象经过点,,三点,则a的值是________.
10.直线经过点, 且平行于直线,则这条直线的解析式为______.
11.若直线y=2x+1平移后过点(-1,2),则平移后直线的解析式为___________________.
12.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
13.如图,将直线向上平移2个单位长度,则平移后的直线的表达式为______.
14.如图,在平面直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,△BOC的面积为_________.
三、解答题
15.已知是关于的一次函数,且当时,;当时,.
(1)求关于的函数表达式
(2)若一次函数的图象与轴、轴分别交于两点, 求的面积.
16.已知是的一次函数,且当时,的值是9;当 时,的值是-3.
(1)求关于的函数关系式;
(2)当时,求的取值范围.
17.已知一次函数的图象经过点和点,且点B在正比例函数的图象上.
(1)求a的值;
(2)求一次函数的解析式;
(3)若,是这个一次函数图象上的两点,试比较与的大小.
18.已知一次函数经过点,O为坐标原点.
(1)求的值;
(2)当函数值时,求的取值范围.
19.已知一次函数的图象与轴交点在轴上方,且随的增大而减小,为整数.
(1)求的值;
(2)写出此一次函数的表达式,并画出函数图象;
(3)若点为此一次函数图象上一点,点是图象与轴交点,且的面积为,求点的坐标.
20.如图,点的坐标为,点在直线上运动.
(1)若点的坐标是,把直线向上平移个单位后,与直线的交点在第一象限,求的取值范围.
(2)当线段最短时,求点的坐标.
答案
一、单选题
A.B.C.D.D.D.D.B.
二、填空题
9. 1.
10.y=2x-2.
11.
12.y=2x+10.
13..
14.4.5.
三、解答题
15.
(1)∵一次函数y=kx+b(k≠0)的图象过点(1,-4),(2,-6).
∴,解得:.
∴这个一次函数的解析式为:y=-2x-2;
(2)令y=0,则x=-1,
∴A( 1,0),OA=1
令x=0,则y=-2,
∴B(0,-2),OB=2
∴S△OAB=OA OB=×1×2=1.
16.
(1)设y=kx+b(k≠0),
得 ,
解得: ,
y=-2x+1,
(2) y=-2x+1,
,
,
,
,
,
,
17.
(1)∵点B(-a,3)在正比例函数y=-3x的图象上,
∴3=-3×(-a),
∴a=1;
(2)由(1)可得点B的坐标为(-1,3),将(-1,3)和(0,2)代入y=kx+b中,
得b=2,代入-k+b=3,解得k=-1,∴一次函数的解析式为y=-x+2;
(3)∵-1<0,∴y随x的增大而减小.
又∵m>m-1,∴y1<y2.
18.
解:(1)把代入中,得,解得;
(2)当时,,解得.
19.
解:(1)∵一次函数的图象与轴交点在轴上方,且随的增大而减小
∴
∴
∵为整数
∴.
(2)∵
∴一次函数的解析式为
∵当时,;当时,
∴函数图像经过、
∴在平面直角坐标系中描出、,再过这两个点做直线
∴可画出一次函数的图象,如图:
.
(3)∵点为一次函数图象上一点
∴设点的坐标为
∵点是图象与轴交点
∴
∴
∵
∴
∴
∴
∴当时,;当时,
∴点的坐标为或,如图
.
20.
(1)设直线的解析式为.
点的坐标为,点的坐标是,
,
解得,
直线的解析式为,
把直线向上平移个单位后得.
由,解得,
即交点为.
由题意,得,
解得;
(2)最短时有,设此时直线的解析式为,将代入,得,解得,
即直线的解析式为,
由,解得,
点坐标为.
