八年级数学上册试题 12.4 综合与实践 一次函数模型的应用-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 12.4 综合与实践 一次函数模型的应用-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 373.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 23:22:02 | ||
图片预览


文档简介
12.4 综合与实践 一次函数模型的应用
一、单选题
1.汽车由A市驶往相距120km的B市,它的平均速度是30km/h,则汽车距B市的路程s(km)与行驶时间t(h)的函数关系式及自变量的取值范围是 ( )
A. B.
C. D.
2.已知等腰三角形周长为40,则腰长y关于底边长x的函数图象是
A.B.C. D.
3.若等腰三角形的周长为20 cm,底边长为x cm,一腰长为y cm,则y与x之间的函数表达式正确的是( )
A.y=20-2x(0<x<20) B.y=20-2x(0<x<10)
C.y=(20-x)(0<x<20) D.y= (20-x)(0<x<10)
4.如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
A.注水前乙容器内水的高度是5厘米
B.甲容器内的水4分钟全部注入乙容器
C.注水2分钟时,甲、乙两个容器中的水的深度相等
D.注水1分钟时,甲容器的水比乙容器的水深5厘米
5.在函数中,给取不同的值,就可以得到不同的直线,那么这些直线必定( )
A.交于同一个点 B.交于无数个点 C.互相平行 D.没有确定的关系
6.某批发部对经销的一种电子元件调查后发现,一天的盈利y(元)与这天的销售量x(个)之间的函数关系的图像如图所示下列说法不正确的是( ).
A.一天售出这种电子元件300个时盈利最大
B.批发部每天的成本是200元
C.批发部每天卖100个时不赔不赚
D.这种电子元件每件盈利5元
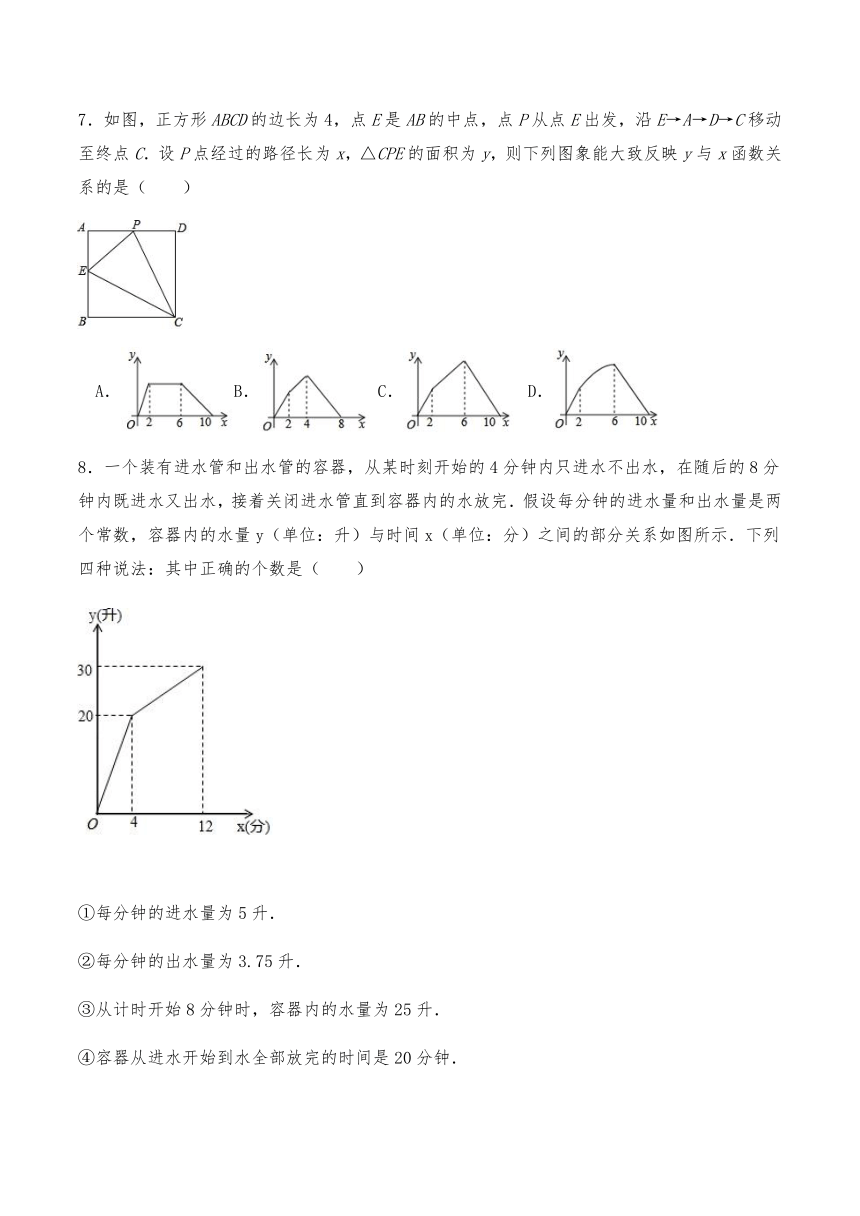
7.如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )
A.B. C. D.
8.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.下列四种说法:其中正确的个数是( )
①每分钟的进水量为5升.
②每分钟的出水量为3.75升.
③从计时开始8分钟时,容器内的水量为25升.
④容器从进水开始到水全部放完的时间是20分钟.
A.1个 B.2个 C.3个 D.4个
二、填空题
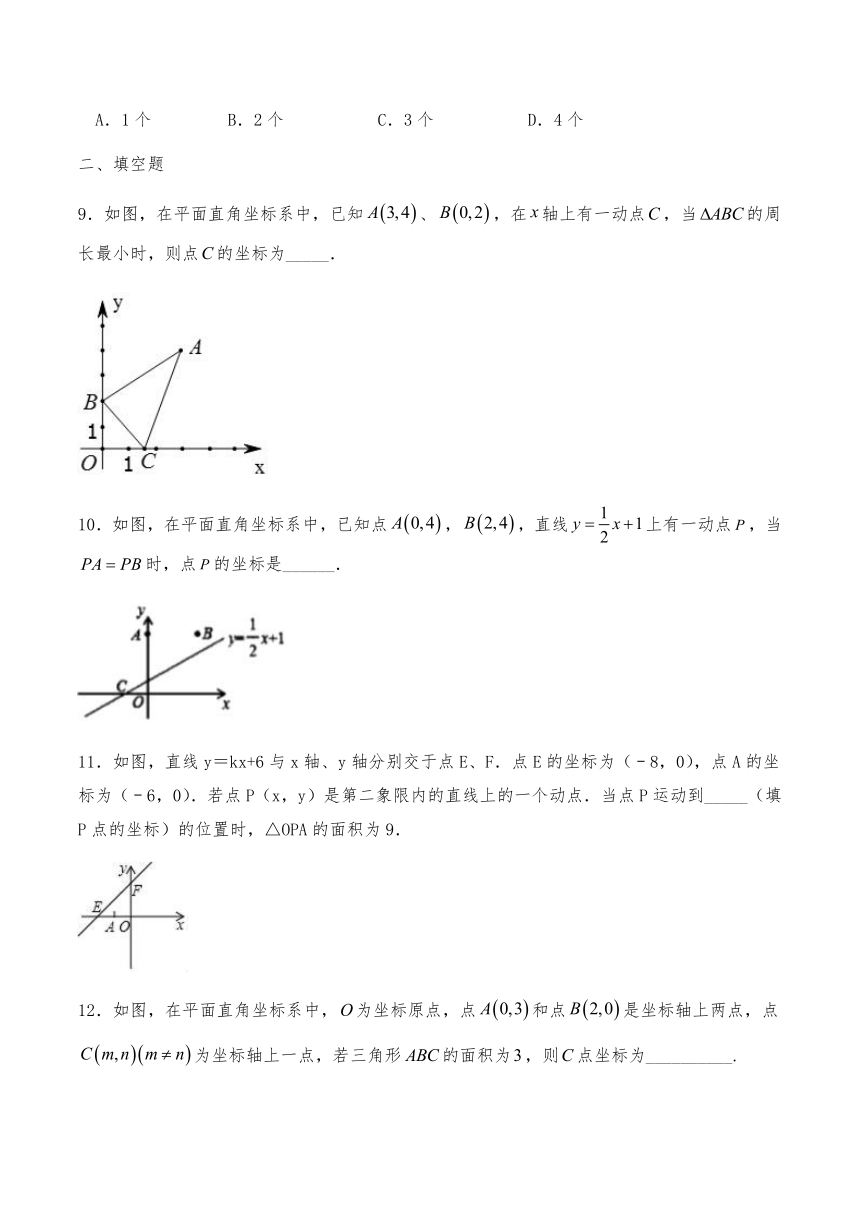
9.如图,在平面直角坐标系中,已知、,在轴上有一动点,当的周长最小时,则点的坐标为_____.
10.如图,在平面直角坐标系中,已知点,,直线上有一动点,当时,点的坐标是______.
11.如图,直线y=kx+6与x轴、y轴分别交于点E、F.点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).若点P(x,y)是第二象限内的直线上的一个动点.当点P运动到_____(填P点的坐标)的位置时,△OPA的面积为9.
12.如图,在平面直角坐标系中,为坐标原点,点和点是坐标轴上两点,点为坐标轴上一点,若三角形的面积为,则点坐标为__________.
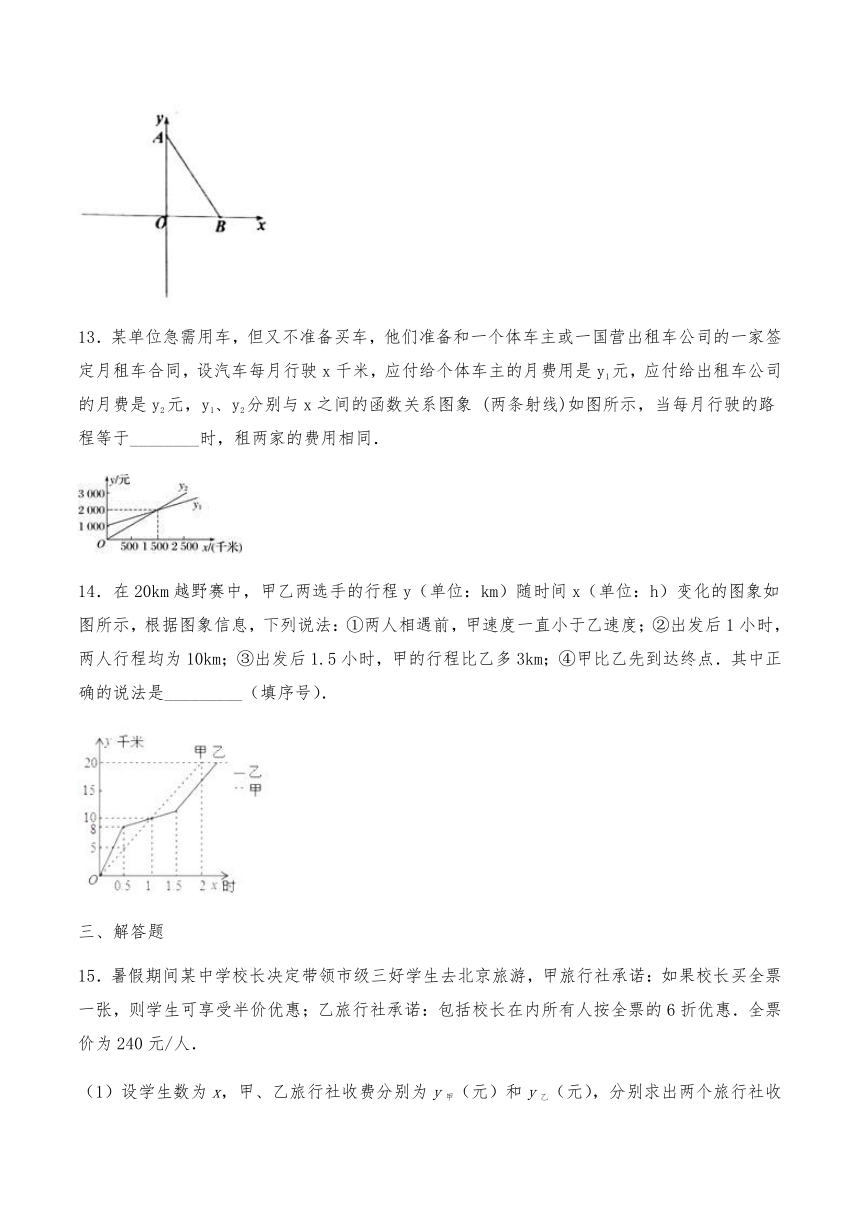
13.某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司的一家签定月租车合同,设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公司的月费是y2元,y1、y2分别与x之间的函数关系图象 (两条射线)如图所示,当每月行驶的路程等于________时,租两家的费用相同.
14.在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图象信息,下列说法:①两人相遇前,甲速度一直小于乙速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的说法是_________(填序号).
三、解答题
15.暑假期间某中学校长决定带领市级三好学生去北京旅游,甲旅行社承诺:如果校长买全票一张,则学生可享受半价优惠;乙旅行社承诺:包括校长在内所有人按全票的6折优惠.全票价为240元/人.
(1)设学生数为x,甲、乙旅行社收费分别为y甲(元)和y乙(元),分别求出两个旅行社收费的表达式;
(2)当有学生20人时,选择哪家旅行社更优惠
16.某公司要印制宣传材料,现有甲、乙两个印刷厂.甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.设印制数量为x(份),甲,乙两印刷厂的收费分别为y1和y2(单位是:元).
(1)请写出y1=______________;y2=_____________.
(2)印制800份宣传材料时,选择哪家印刷厂比较合算?并说明理由.
17.如图,平面直角坐标系中,过点的直线与直线相交于点,动点在线段和射线上运动.
(1)求直线的表达式.
(2)求的面积.
(3)直接写出使的面积是面积的的点坐标.
18.某学校举行数学竞赛,需购买两种奖品共160件,其中种奖品的单价为12元,种奖品的单价为8元,且购买种奖品的数量不大于种奖品数量的3倍,假设购买种奖品的数量为件.
(1)根据题意填空:
购买种奖品的费用为___(元);
购买种奖品的费用为___(元);
(2)若购买两种奖品所需的总费用为元,试求与的函数关系式,并求出的取值范围;
(3)问两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
19.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)乙队开挖到30m时,用了_____ h. 开挖6h时甲队比乙队多挖了____ m;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)当x 为何值时,甲、 乙两队在 施工过程中所挖河渠的长度相等
20.端午节放假期间,某学校计划租用辆客车送名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车辆,租车总费用为元.
甲种客车 乙种客车
载客量(人/辆)
租金(元/辆)
(1)求出(元)与(辆)之间函数关系式;
(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
答案
一、单选题
D.D.D.D.C.D.C.D.
二、填空题
9.(1,0).
10. .
11.(﹣4,3).
12.(0,6)或(4,0).
13.1500.
14.②③④
三、解答题
15.
解:(1)依题意可得:y甲=240+240x×50%=120 x+240
y乙=(240+240x)×60%=144x+144
所以y甲=120 x+240; y乙=144x+144.
(2)当x=20,y甲=120×20+240=2640(元)
y乙=144×20+144=3024(元)
此时y甲<y乙
故甲旅行更优惠.
16.
(1)由题意可知:
甲厂每份材料收1元印制费,另收1500元制版,则
乙场每份材料收2.5元印制费,不收制版费,则
(2)当时,,,乙印刷厂费用较低.
17.
解:(1) 设直线的解析式是,
根据题意得:
解得:,
则直线的解析式是:;
(2);
(3) 设OA的解析式是,则,
解得:,
则直线的解析式是:,
当的面积是的面积的时,
∴M的横坐标是,
在中,当时, ,则M的坐标是;
在中, 当则 则M的坐标是
在中,当时,,则M的坐标是.
综上所述:M的坐标是:或或.
18.
解:(1)根据题意填空:
购买种奖品的费用为 (元);
购买种奖品的费用为(元);
(2)根据题意得,
∴
,解得:
由题意得:
∴;
(3)∵
∴随的增大而增大
∵
∴当时,(元)
∴当购买种奖品40件,种奖品120件时,所需费用最少,最少费用为1440元 .
故答案为:(1),;(2),;(3)购买种奖品40件,种奖品120件时,所需费用最少,最少费用为1440元.
19.
解:(1)依题意得乙队开挖到30m时,用了2h,
开挖6h时甲队比乙队多挖了60-50=10m;
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式y=k1x,
由图可知,函数图象过点(6,60),
∴6k1=60,
解得k1=10,
∴y=10x,
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴ ,
解得 ,
∴y=5x+20;
(3)由题意,得10x=5x+20,
解得x=4(h).
∴当x为4h时,甲、乙两队所挖的河渠长度相等.
故答案为:(1)2,10;(2)①y=10x,②y=5x+20;(3)x为4h时,甲、乙两队所挖的河渠长度相等.
20.
解:(1)设租用甲种客车辆,则租用乙种客车辆,
由题意可得出:;
(2)由得:.
又,
∴x的取值范围是:,且为整数;
(3),且为整数,
∴x取或或
中
随的增大而增大
当时,的值最小.
其最小值元.
则租用甲种客车辆,租用乙种客车辆,所需的费用最低,最低费用元.
故答案为(1);(2),且为整数;(3)租用甲种客车辆,租用乙种客车辆,所需的费用最低,最低费用元.
一、单选题
1.汽车由A市驶往相距120km的B市,它的平均速度是30km/h,则汽车距B市的路程s(km)与行驶时间t(h)的函数关系式及自变量的取值范围是 ( )
A. B.
C. D.
2.已知等腰三角形周长为40,则腰长y关于底边长x的函数图象是
A.B.C. D.
3.若等腰三角形的周长为20 cm,底边长为x cm,一腰长为y cm,则y与x之间的函数表达式正确的是( )
A.y=20-2x(0<x<20) B.y=20-2x(0<x<10)
C.y=(20-x)(0<x<20) D.y= (20-x)(0<x<10)
4.如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
A.注水前乙容器内水的高度是5厘米
B.甲容器内的水4分钟全部注入乙容器
C.注水2分钟时,甲、乙两个容器中的水的深度相等
D.注水1分钟时,甲容器的水比乙容器的水深5厘米
5.在函数中,给取不同的值,就可以得到不同的直线,那么这些直线必定( )
A.交于同一个点 B.交于无数个点 C.互相平行 D.没有确定的关系
6.某批发部对经销的一种电子元件调查后发现,一天的盈利y(元)与这天的销售量x(个)之间的函数关系的图像如图所示下列说法不正确的是( ).
A.一天售出这种电子元件300个时盈利最大
B.批发部每天的成本是200元
C.批发部每天卖100个时不赔不赚
D.这种电子元件每件盈利5元
7.如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )
A.B. C. D.
8.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.下列四种说法:其中正确的个数是( )
①每分钟的进水量为5升.
②每分钟的出水量为3.75升.
③从计时开始8分钟时,容器内的水量为25升.
④容器从进水开始到水全部放完的时间是20分钟.
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,在平面直角坐标系中,已知、,在轴上有一动点,当的周长最小时,则点的坐标为_____.
10.如图,在平面直角坐标系中,已知点,,直线上有一动点,当时,点的坐标是______.
11.如图,直线y=kx+6与x轴、y轴分别交于点E、F.点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).若点P(x,y)是第二象限内的直线上的一个动点.当点P运动到_____(填P点的坐标)的位置时,△OPA的面积为9.
12.如图,在平面直角坐标系中,为坐标原点,点和点是坐标轴上两点,点为坐标轴上一点,若三角形的面积为,则点坐标为__________.
13.某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司的一家签定月租车合同,设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公司的月费是y2元,y1、y2分别与x之间的函数关系图象 (两条射线)如图所示,当每月行驶的路程等于________时,租两家的费用相同.
14.在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图象信息,下列说法:①两人相遇前,甲速度一直小于乙速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的说法是_________(填序号).
三、解答题
15.暑假期间某中学校长决定带领市级三好学生去北京旅游,甲旅行社承诺:如果校长买全票一张,则学生可享受半价优惠;乙旅行社承诺:包括校长在内所有人按全票的6折优惠.全票价为240元/人.
(1)设学生数为x,甲、乙旅行社收费分别为y甲(元)和y乙(元),分别求出两个旅行社收费的表达式;
(2)当有学生20人时,选择哪家旅行社更优惠
16.某公司要印制宣传材料,现有甲、乙两个印刷厂.甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.设印制数量为x(份),甲,乙两印刷厂的收费分别为y1和y2(单位是:元).
(1)请写出y1=______________;y2=_____________.
(2)印制800份宣传材料时,选择哪家印刷厂比较合算?并说明理由.
17.如图,平面直角坐标系中,过点的直线与直线相交于点,动点在线段和射线上运动.
(1)求直线的表达式.
(2)求的面积.
(3)直接写出使的面积是面积的的点坐标.
18.某学校举行数学竞赛,需购买两种奖品共160件,其中种奖品的单价为12元,种奖品的单价为8元,且购买种奖品的数量不大于种奖品数量的3倍,假设购买种奖品的数量为件.
(1)根据题意填空:
购买种奖品的费用为___(元);
购买种奖品的费用为___(元);
(2)若购买两种奖品所需的总费用为元,试求与的函数关系式,并求出的取值范围;
(3)问两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
19.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)乙队开挖到30m时,用了_____ h. 开挖6h时甲队比乙队多挖了____ m;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)当x 为何值时,甲、 乙两队在 施工过程中所挖河渠的长度相等
20.端午节放假期间,某学校计划租用辆客车送名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车辆,租车总费用为元.
甲种客车 乙种客车
载客量(人/辆)
租金(元/辆)
(1)求出(元)与(辆)之间函数关系式;
(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
答案
一、单选题
D.D.D.D.C.D.C.D.
二、填空题
9.(1,0).
10. .
11.(﹣4,3).
12.(0,6)或(4,0).
13.1500.
14.②③④
三、解答题
15.
解:(1)依题意可得:y甲=240+240x×50%=120 x+240
y乙=(240+240x)×60%=144x+144
所以y甲=120 x+240; y乙=144x+144.
(2)当x=20,y甲=120×20+240=2640(元)
y乙=144×20+144=3024(元)
此时y甲<y乙
故甲旅行更优惠.
16.
(1)由题意可知:
甲厂每份材料收1元印制费,另收1500元制版,则
乙场每份材料收2.5元印制费,不收制版费,则
(2)当时,,,乙印刷厂费用较低.
17.
解:(1) 设直线的解析式是,
根据题意得:
解得:,
则直线的解析式是:;
(2);
(3) 设OA的解析式是,则,
解得:,
则直线的解析式是:,
当的面积是的面积的时,
∴M的横坐标是,
在中,当时, ,则M的坐标是;
在中, 当则 则M的坐标是
在中,当时,,则M的坐标是.
综上所述:M的坐标是:或或.
18.
解:(1)根据题意填空:
购买种奖品的费用为 (元);
购买种奖品的费用为(元);
(2)根据题意得,
∴
,解得:
由题意得:
∴;
(3)∵
∴随的增大而增大
∵
∴当时,(元)
∴当购买种奖品40件,种奖品120件时,所需费用最少,最少费用为1440元 .
故答案为:(1),;(2),;(3)购买种奖品40件,种奖品120件时,所需费用最少,最少费用为1440元.
19.
解:(1)依题意得乙队开挖到30m时,用了2h,
开挖6h时甲队比乙队多挖了60-50=10m;
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式y=k1x,
由图可知,函数图象过点(6,60),
∴6k1=60,
解得k1=10,
∴y=10x,
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴ ,
解得 ,
∴y=5x+20;
(3)由题意,得10x=5x+20,
解得x=4(h).
∴当x为4h时,甲、乙两队所挖的河渠长度相等.
故答案为:(1)2,10;(2)①y=10x,②y=5x+20;(3)x为4h时,甲、乙两队所挖的河渠长度相等.
20.
解:(1)设租用甲种客车辆,则租用乙种客车辆,
由题意可得出:;
(2)由得:.
又,
∴x的取值范围是:,且为整数;
(3),且为整数,
∴x取或或
中
随的增大而增大
当时,的值最小.
其最小值元.
则租用甲种客车辆,租用乙种客车辆,所需的费用最低,最低费用元.
故答案为(1);(2),且为整数;(3)租用甲种客车辆,租用乙种客车辆,所需的费用最低,最低费用元.
