沪科版八年级数学上册 14.2 两边及其夹角分别相等的两个三角形 练习(2课时、含答案)
文档属性
| 名称 | 沪科版八年级数学上册 14.2 两边及其夹角分别相等的两个三角形 练习(2课时、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 736.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 10:59:42 | ||
图片预览




文档简介
14.2 两边及其夹角分别相等的两个三角形
第1课时
一、单选题
1.下列条件中,不能判断的是( )
A. B.
C. D.
2.如图,如图,点,,,同在一条直线上,,,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
3.如图,已知AC=DB,下列四个条件①∠A=∠D;②∠ABD=∠DCA;③∠ACB=∠DBC;④∠ABC=∠DCB,其中能使△ABC≌△DCB的有( )
A.1个 B.2个 C.3个 D.4个
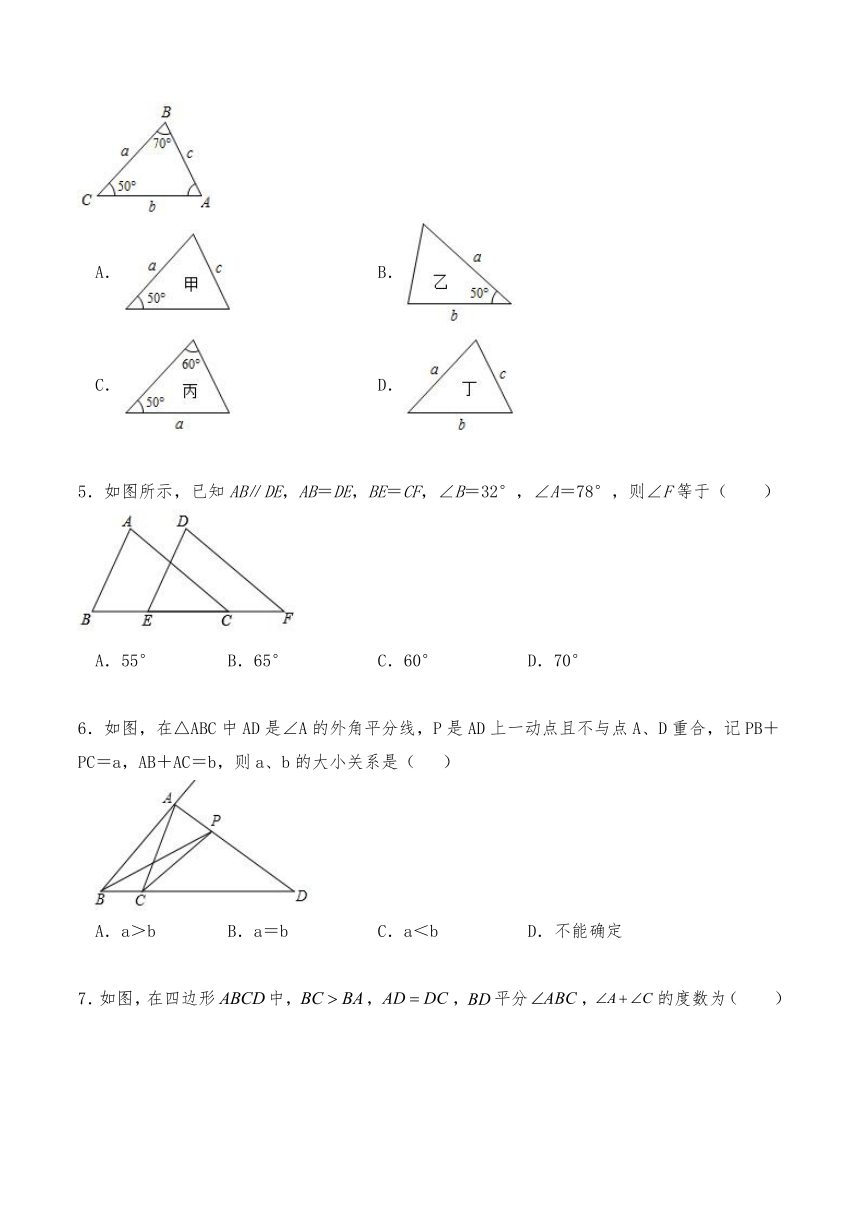
4.下列各图中a、b、c为△ABC的边长,根据图中标注数据,判断甲、乙、丙、丁四个三角形和如图△ABC不一定全等的是( )
A. B.
C. D.
5.如图所示,已知AB∥DE,AB=DE,BE=CF,∠B=32°,∠A=78°,则∠F等于( )
A.55° B.65° C.60° D.70°
6.如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
A.a>b B.a=b C.a<b D.不能确定
7.如图,在四边形中,,,平分,的度数为( )
A.120° B.150° C.180° D.200°
8.如图1,已知,为的角平分线上面一点,连接,;如图2,已知,、为的角平分线上面两点,连接,,,;如图3,已知,、、为的角平分线上面三点,连接,,,,,;…,依次规律,第个图形中有全等三角形的对数是( ).
A. B. C. D.
二、填空题
9.如图,,要用“”判定,则可加上条件__________.
10.为了测出池塘两端A,B的距离,毛毛在地面上选择了点O,D,C,使,,且点A,O,C和点B,O,D分别都在一条直线上,毛毛量出了D,C的距离为68米,则A,B的距离为_____米.
11.如图所示,,以点为圆心,以适当长为半径作弧分别交,于,两点;分别以,为圆心,以大于的长为半径作弧,两弧相交于点;以为端点作射线,在射线上取点,连接、.若测得,则_______.
12.如图,在2×2的正方形网格中,线段AB、CD的端点均在格点上,则∠1+∠2=_____°.
13.如图所示,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=25°,则∠BDC=_____.
14.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
三、解答题
15.如图,在△ABC和△DCE中,点B,C,E在一条直线上,且AB∥DC,AB=DC,BC=CE.求证:∠A=∠D.
16.如图,在中,于,于,是上一点,,是延长线一点,,连接,.
(1)求证:;
(2)探求线段,有什么关系,并证明.
17.如图,与交于点,,,垂足为,垂足为.
(1)求证:;
(2)求证:共线.
18.在等腰和等腰中,,连为中点,连.
(1)如图1,请写出与的关系,并说明理由;
(2)将图1中的旋转至图2的位置,其他条件不变,(1)中结论是否成立?请说明理由.
19.如图, 已知, 是直线上的点,过点作, 并截取, 连接DC,DF,CF.
(1)判断的形状并证明.
(2)若,,求的长.
20.如图,有两根竹杆AC、BD相距18米,AC=6米,AC⊥AB,DB⊥AB,现有两个动点P、Q同时从B点出发,点P以每秒2米的速度向点D运动,点Q以每秒1米的速度向点A运动,在线段AB上有一点Q.(包括点A和点B)
(1)当P、Q两点运动6秒后,CQ与PQ有怎样的关系
(2)当P、Q两点运动t秒后,使以C、A、Q为顶点的三角形与以P、B、Q为顶点的三角形全等,直接写出t的值______.
第2课时
一、单选题
1.如图,某同学把一块三角形的玻璃打碎成3块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是______,这么做的依据是______.( )
A.带①去, B.带②去,
C.带③去, D.①②③都带去,
2.如图,点F,A,D,C在同一直线上,,且,,已知,,则的长为( )
A.5 B.6 C.6.5 D.7
3.如图,要测量河宽的距离,可以在的垂线上取两点,,使,再作的垂线,且使,,在同一条直线上,可得,用于判定两三角形全等的最佳依据是( )
A. B. C. D.
4.小红用如图所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,BO=OC,CD⊥BC,点A、O、D在同一直线上,就能保证△ABO≌△DCO,从而可通过测量CD的长度得知小河的宽度AB.在这个问题中,可作为证明△ABO≌△DCO的依据的是( )
A.SSS B.ASA
C.SAS D.HL
5.如图,是上一点,交于点,,,若,,则的长是( )
A.6 B. C.3 D.4
6.如图,在Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③PH=PD;④连接CP,CP平分∠ACB其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
7.如图,四边形AFDC是正方形,和都是直角,且E,A,B三点共线,,则图中阴影部分的面积是( )
A.12 B.10 C.8 D.6
8.为了丰富中小学生的业余生活,某社区要在如图所示的直线上建一图书室,该社区有一小学在点C处,有一中学在点D处,已知于点A,于点B,且,当两所学校到图书室的距离相等,且点C、D与图书室视角为90°时,图书室应该建在距离点A( )处.
A.12 B.11 C.10.5 D.10
二、填空题
9.如图所示,某三角形材料断裂成A、B、C三块,现要配置与原材料一样的三角形材料,应该选用材料____,理由是____.
10.如图,已知平分,,则根据“_________”,就可判断.
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有①,②,③,④的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形,应该带第____________块.
12.如图,,与交于点O,在不添加任何辅助线的前提下要使,则需添加条件_____________________.
13.如图,△ABC的面积为1cm2,AP垂直∠ABC的平分线BP于P,则△PBC的面积为___.
14.在中,,,,在上取一点,使,过点作交的延长线于点,若,则________.
三、解答题
15.如图点B,F,C,E,在同一条直线上,点A,D在直线BE的两侧,AB平行于DE,AC平行于DF,BF=CE,求证:△ABC≌△DEF.
16.如图,在和中,,,.
求证:.
17.如图,在△ABC中,D是线段BC的中点,F,E分别是AD及其延长线上的点,且CF∥BE.求证:DE=DF
18.如图,点、、在同一直线上,,,
求证:(1);
(2).
19.ABC和DBC中,∠BAC=∠BDC=90°,延长CD、BA交于点E.
(1)如图1,若AB=AC,试说明BO=EC;
(2)如图2,∠MON为直角,它的两边OM、ON分别与AB、EC所在直线交于点M、N,如果OM=ON,那么BM与CO是否相等?请说明理由.
20.已知:平面直角坐标系中,点,,点为轴正半轴上一动点,过点作交轴于点.
(1)线段___,线段___(直接填空).
(2)如图①,若点的坐标为,试求点的坐标.
(3)如图②,若点在轴正半轴上运动,且,其它条件不变,连,求证:平分.
第1课时答案
一、单选题
B.C.A.A.D.A.C.C.
二、填空题
9.AD=BD.
10.68.
11.55°.
12.90°.
13.70°.
14.3或.
三、解答题
15.
证明:∵AB∥DC,
∴∠B=∠DCE,
又∵AB=DC,BC=CE ,
∴△ABC≌△DCE(SAS),
∴∠A=∠D.
16.
解:(1)∵于,于,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,∠ACE+∠BAD=90°,
∴,
(2)结论:AF=AG,AF⊥AG.理由如下:
在△ABF和△GCA中,,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠GAC=∠AFB,
∵∠AFB=∠ADB+∠FAD,∠GAC=∠GAF+∠FAD,
∴∠GAF=∠ADF,
∵∠ADF=90°,
∴∠GAF=90°,
∴AG⊥AF,AG=AF.
17.
证明:(1)在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD;
(2)∵△AOB≌△DOC,
∴∠A=∠D,
∴AB∥CD,
∵OE⊥AB,
∴OE⊥CD,
∵OF⊥CD,OE和OF相交于点O,
∴E、O、F三点共线.
18.
(1)解:OM=,理由如下:
如图OM至E,使ME=OM,连接DE,AE
∵AM=DM,EM=OM,
∴四边形AODE为平行四边形,
∴AO=DE,
又∵AO=BO,
∴OB=DE,
∵∠BOC+∠AOD=360°-∠COD-∠AOB=180°,
又∠EDO+∠DOA=180°,
∴∠BOC=∠EDO,
又OC=OD,
在△BOC和△EDO中,
∴△BOC≌△EDO,
∴BC=OE,
又∵OM=OE
∴OM=BC;
(2)(1)中结论任然成立,理由如下:
延长OM至E,使ME=MO,连接DE,AE
∵AM=DM,EM=OM,
AODE为平行四边形,
∴AO=DE
又∵AO=BO,
∴OB=DE,
∵∠BOC+∠AOD=∠AOB+∠COD=180°,
又∠EDO+∠DOA=180°,
∴∠BOC=∠EDO,
又OC=OD,
在△BOC和△EDO中,
∴△BOC≌△EDO,
∴BC=OE,
又∵OM=OE,
∴OM=BC;
19.
解:(1)△CDF为等腰直角三角形.理由如下:
∵AF⊥AB,
∴∠DAF=90°,
∵,
∴∠CBD=90°=∠DAF,
在△ADF和△BCD中,
AF=DB,∠DAF=∠CBD,AB=BC,
∴△ADF≌△BCD,
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴△CDF为等腰直角三角形;
(2)∵△ADF≌△BCD,
∴AD=BC=6,AF=BD=2,
∴AB=AD BD=6 2=4.
20.
(1)CQ⊥PQ,
证明:当P、Q两点运动6秒后,
则BQ=6,BP=12,
∴AQ=18-6=12,
∵AC⊥AB,DB⊥AB,
∴∠CAQ =∠QBP=90,
在△AQC和△BPQ中,
,
∴△AQC≌△BPQ(SAS),
∴∠AQC =∠BPQ,CQ=PQ
∵∠BPQ +∠BQP=90,
∴∠AQC +∠BQP=90,
∴CQ⊥PQ;
综上所述,CQ⊥PQ且CQ=PQ;
(2)根据题意,BQ=t,BP=2t,则AQ=18-t,
当△AQC≌△BPQ时,AQ=BP,即18-t=2t,
解得:t=6;
当△AQC≌△BQP时,AQ=BQ,即18-t=t,
解得:t=9;
此时所用时间为9秒,AC=BP=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故答案为:6.
第2课时答案
一、单选题
C.C.D.B.D.D.C.A.
二、填空题
9.C,ASA.
10.AAS.
11.①
12.(答案不唯一)
13. cm2.
14.3.
三、解答题
15.
证明:∵AB平行于DE,AC平行于DF,
∴∠B=∠E,∠ACB=∠DFE,
∵BF=CE,∴BF+FC=CE+CF,即BC=EF,
∴△ABC≌△DEF .
16.
证明:,
,
.
在和中,
.
17.
∵CF∥BE
∴∠FCD=∠EBD
∵D是线段BC的中点
∴CD=BD
又∵∠CDF=∠BDE
∴△CDF≌△BDE
∴ CF=BE
18.
(1)∵,
∴;
(2)∵,
∴,
在ΔABC和ΔDEC中,
∴ΔABC≌ΔCED(AAS),
∴BC=ED.
19.
解:(1)∵∠BAC=∠BDC=90°,
∴∠ABO+∠AOB=∠DCO+∠DOC=90°,
∵∠AOB=∠DOC,
∴∠ABO=∠DCO,
∵∠EAC=180°﹣∠BAC=90°,
∴∠BAO=∠EAC,
在△BAO和△CAE中,
,
∴△BAO≌△CAE(ASA),
∴BO=CE;
(2)相等.理由如下:
∵∠MON=∠BAC=90°,
∴∠AMO+∠AOM=∠AOM+∠AON=90°,
∴∠AMO=∠AON,
∴∠BMO=∠NOC,
由(1)知∠ABO=∠DCO,
在△BOM和△CNO中,
,
∴△BOM≌△CNO(AAS),
∴BM=CO.
20.
(1)点,,;
(2)由题知:,
交轴于点,,,
在与中,
,
的坐标为;
(3)由题可知,点在轴正半轴上运动时,总有,则总有成立,
如图,在图②中作,,
在与中,
,
,
平分
第1课时
一、单选题
1.下列条件中,不能判断的是( )
A. B.
C. D.
2.如图,如图,点,,,同在一条直线上,,,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
3.如图,已知AC=DB,下列四个条件①∠A=∠D;②∠ABD=∠DCA;③∠ACB=∠DBC;④∠ABC=∠DCB,其中能使△ABC≌△DCB的有( )
A.1个 B.2个 C.3个 D.4个
4.下列各图中a、b、c为△ABC的边长,根据图中标注数据,判断甲、乙、丙、丁四个三角形和如图△ABC不一定全等的是( )
A. B.
C. D.
5.如图所示,已知AB∥DE,AB=DE,BE=CF,∠B=32°,∠A=78°,则∠F等于( )
A.55° B.65° C.60° D.70°
6.如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
A.a>b B.a=b C.a<b D.不能确定
7.如图,在四边形中,,,平分,的度数为( )
A.120° B.150° C.180° D.200°
8.如图1,已知,为的角平分线上面一点,连接,;如图2,已知,、为的角平分线上面两点,连接,,,;如图3,已知,、、为的角平分线上面三点,连接,,,,,;…,依次规律,第个图形中有全等三角形的对数是( ).
A. B. C. D.
二、填空题
9.如图,,要用“”判定,则可加上条件__________.
10.为了测出池塘两端A,B的距离,毛毛在地面上选择了点O,D,C,使,,且点A,O,C和点B,O,D分别都在一条直线上,毛毛量出了D,C的距离为68米,则A,B的距离为_____米.
11.如图所示,,以点为圆心,以适当长为半径作弧分别交,于,两点;分别以,为圆心,以大于的长为半径作弧,两弧相交于点;以为端点作射线,在射线上取点,连接、.若测得,则_______.
12.如图,在2×2的正方形网格中,线段AB、CD的端点均在格点上,则∠1+∠2=_____°.
13.如图所示,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=25°,则∠BDC=_____.
14.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
三、解答题
15.如图,在△ABC和△DCE中,点B,C,E在一条直线上,且AB∥DC,AB=DC,BC=CE.求证:∠A=∠D.
16.如图,在中,于,于,是上一点,,是延长线一点,,连接,.
(1)求证:;
(2)探求线段,有什么关系,并证明.
17.如图,与交于点,,,垂足为,垂足为.
(1)求证:;
(2)求证:共线.
18.在等腰和等腰中,,连为中点,连.
(1)如图1,请写出与的关系,并说明理由;
(2)将图1中的旋转至图2的位置,其他条件不变,(1)中结论是否成立?请说明理由.
19.如图, 已知, 是直线上的点,过点作, 并截取, 连接DC,DF,CF.
(1)判断的形状并证明.
(2)若,,求的长.
20.如图,有两根竹杆AC、BD相距18米,AC=6米,AC⊥AB,DB⊥AB,现有两个动点P、Q同时从B点出发,点P以每秒2米的速度向点D运动,点Q以每秒1米的速度向点A运动,在线段AB上有一点Q.(包括点A和点B)
(1)当P、Q两点运动6秒后,CQ与PQ有怎样的关系
(2)当P、Q两点运动t秒后,使以C、A、Q为顶点的三角形与以P、B、Q为顶点的三角形全等,直接写出t的值______.
第2课时
一、单选题
1.如图,某同学把一块三角形的玻璃打碎成3块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是______,这么做的依据是______.( )
A.带①去, B.带②去,
C.带③去, D.①②③都带去,
2.如图,点F,A,D,C在同一直线上,,且,,已知,,则的长为( )
A.5 B.6 C.6.5 D.7
3.如图,要测量河宽的距离,可以在的垂线上取两点,,使,再作的垂线,且使,,在同一条直线上,可得,用于判定两三角形全等的最佳依据是( )
A. B. C. D.
4.小红用如图所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,BO=OC,CD⊥BC,点A、O、D在同一直线上,就能保证△ABO≌△DCO,从而可通过测量CD的长度得知小河的宽度AB.在这个问题中,可作为证明△ABO≌△DCO的依据的是( )
A.SSS B.ASA
C.SAS D.HL
5.如图,是上一点,交于点,,,若,,则的长是( )
A.6 B. C.3 D.4
6.如图,在Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③PH=PD;④连接CP,CP平分∠ACB其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
7.如图,四边形AFDC是正方形,和都是直角,且E,A,B三点共线,,则图中阴影部分的面积是( )
A.12 B.10 C.8 D.6
8.为了丰富中小学生的业余生活,某社区要在如图所示的直线上建一图书室,该社区有一小学在点C处,有一中学在点D处,已知于点A,于点B,且,当两所学校到图书室的距离相等,且点C、D与图书室视角为90°时,图书室应该建在距离点A( )处.
A.12 B.11 C.10.5 D.10
二、填空题
9.如图所示,某三角形材料断裂成A、B、C三块,现要配置与原材料一样的三角形材料,应该选用材料____,理由是____.
10.如图,已知平分,,则根据“_________”,就可判断.
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有①,②,③,④的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形,应该带第____________块.
12.如图,,与交于点O,在不添加任何辅助线的前提下要使,则需添加条件_____________________.
13.如图,△ABC的面积为1cm2,AP垂直∠ABC的平分线BP于P,则△PBC的面积为___.
14.在中,,,,在上取一点,使,过点作交的延长线于点,若,则________.
三、解答题
15.如图点B,F,C,E,在同一条直线上,点A,D在直线BE的两侧,AB平行于DE,AC平行于DF,BF=CE,求证:△ABC≌△DEF.
16.如图,在和中,,,.
求证:.
17.如图,在△ABC中,D是线段BC的中点,F,E分别是AD及其延长线上的点,且CF∥BE.求证:DE=DF
18.如图,点、、在同一直线上,,,
求证:(1);
(2).
19.ABC和DBC中,∠BAC=∠BDC=90°,延长CD、BA交于点E.
(1)如图1,若AB=AC,试说明BO=EC;
(2)如图2,∠MON为直角,它的两边OM、ON分别与AB、EC所在直线交于点M、N,如果OM=ON,那么BM与CO是否相等?请说明理由.
20.已知:平面直角坐标系中,点,,点为轴正半轴上一动点,过点作交轴于点.
(1)线段___,线段___(直接填空).
(2)如图①,若点的坐标为,试求点的坐标.
(3)如图②,若点在轴正半轴上运动,且,其它条件不变,连,求证:平分.
第1课时答案
一、单选题
B.C.A.A.D.A.C.C.
二、填空题
9.AD=BD.
10.68.
11.55°.
12.90°.
13.70°.
14.3或.
三、解答题
15.
证明:∵AB∥DC,
∴∠B=∠DCE,
又∵AB=DC,BC=CE ,
∴△ABC≌△DCE(SAS),
∴∠A=∠D.
16.
解:(1)∵于,于,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,∠ACE+∠BAD=90°,
∴,
(2)结论:AF=AG,AF⊥AG.理由如下:
在△ABF和△GCA中,,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠GAC=∠AFB,
∵∠AFB=∠ADB+∠FAD,∠GAC=∠GAF+∠FAD,
∴∠GAF=∠ADF,
∵∠ADF=90°,
∴∠GAF=90°,
∴AG⊥AF,AG=AF.
17.
证明:(1)在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD;
(2)∵△AOB≌△DOC,
∴∠A=∠D,
∴AB∥CD,
∵OE⊥AB,
∴OE⊥CD,
∵OF⊥CD,OE和OF相交于点O,
∴E、O、F三点共线.
18.
(1)解:OM=,理由如下:
如图OM至E,使ME=OM,连接DE,AE
∵AM=DM,EM=OM,
∴四边形AODE为平行四边形,
∴AO=DE,
又∵AO=BO,
∴OB=DE,
∵∠BOC+∠AOD=360°-∠COD-∠AOB=180°,
又∠EDO+∠DOA=180°,
∴∠BOC=∠EDO,
又OC=OD,
在△BOC和△EDO中,
∴△BOC≌△EDO,
∴BC=OE,
又∵OM=OE
∴OM=BC;
(2)(1)中结论任然成立,理由如下:
延长OM至E,使ME=MO,连接DE,AE
∵AM=DM,EM=OM,
AODE为平行四边形,
∴AO=DE
又∵AO=BO,
∴OB=DE,
∵∠BOC+∠AOD=∠AOB+∠COD=180°,
又∠EDO+∠DOA=180°,
∴∠BOC=∠EDO,
又OC=OD,
在△BOC和△EDO中,
∴△BOC≌△EDO,
∴BC=OE,
又∵OM=OE,
∴OM=BC;
19.
解:(1)△CDF为等腰直角三角形.理由如下:
∵AF⊥AB,
∴∠DAF=90°,
∵,
∴∠CBD=90°=∠DAF,
在△ADF和△BCD中,
AF=DB,∠DAF=∠CBD,AB=BC,
∴△ADF≌△BCD,
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴△CDF为等腰直角三角形;
(2)∵△ADF≌△BCD,
∴AD=BC=6,AF=BD=2,
∴AB=AD BD=6 2=4.
20.
(1)CQ⊥PQ,
证明:当P、Q两点运动6秒后,
则BQ=6,BP=12,
∴AQ=18-6=12,
∵AC⊥AB,DB⊥AB,
∴∠CAQ =∠QBP=90,
在△AQC和△BPQ中,
,
∴△AQC≌△BPQ(SAS),
∴∠AQC =∠BPQ,CQ=PQ
∵∠BPQ +∠BQP=90,
∴∠AQC +∠BQP=90,
∴CQ⊥PQ;
综上所述,CQ⊥PQ且CQ=PQ;
(2)根据题意,BQ=t,BP=2t,则AQ=18-t,
当△AQC≌△BPQ时,AQ=BP,即18-t=2t,
解得:t=6;
当△AQC≌△BQP时,AQ=BQ,即18-t=t,
解得:t=9;
此时所用时间为9秒,AC=BP=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故答案为:6.
第2课时答案
一、单选题
C.C.D.B.D.D.C.A.
二、填空题
9.C,ASA.
10.AAS.
11.①
12.(答案不唯一)
13. cm2.
14.3.
三、解答题
15.
证明:∵AB平行于DE,AC平行于DF,
∴∠B=∠E,∠ACB=∠DFE,
∵BF=CE,∴BF+FC=CE+CF,即BC=EF,
∴△ABC≌△DEF .
16.
证明:,
,
.
在和中,
.
17.
∵CF∥BE
∴∠FCD=∠EBD
∵D是线段BC的中点
∴CD=BD
又∵∠CDF=∠BDE
∴△CDF≌△BDE
∴ CF=BE
18.
(1)∵,
∴;
(2)∵,
∴,
在ΔABC和ΔDEC中,
∴ΔABC≌ΔCED(AAS),
∴BC=ED.
19.
解:(1)∵∠BAC=∠BDC=90°,
∴∠ABO+∠AOB=∠DCO+∠DOC=90°,
∵∠AOB=∠DOC,
∴∠ABO=∠DCO,
∵∠EAC=180°﹣∠BAC=90°,
∴∠BAO=∠EAC,
在△BAO和△CAE中,
,
∴△BAO≌△CAE(ASA),
∴BO=CE;
(2)相等.理由如下:
∵∠MON=∠BAC=90°,
∴∠AMO+∠AOM=∠AOM+∠AON=90°,
∴∠AMO=∠AON,
∴∠BMO=∠NOC,
由(1)知∠ABO=∠DCO,
在△BOM和△CNO中,
,
∴△BOM≌△CNO(AAS),
∴BM=CO.
20.
(1)点,,;
(2)由题知:,
交轴于点,,,
在与中,
,
的坐标为;
(3)由题可知,点在轴正半轴上运动时,总有,则总有成立,
如图,在图②中作,,
在与中,
,
,
平分
