图形的相似[下学期]
图片预览


文档简介
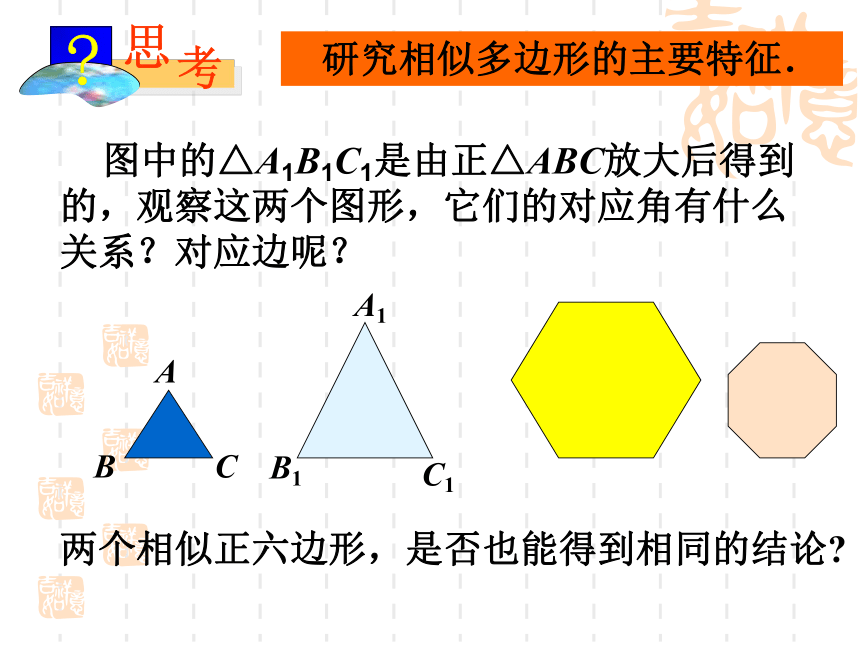
课件11张PPT。27.1 图形的相似 研究相似多边形的主要特征. 图中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?两个相似正六边形,是否也能得到相同的结论?
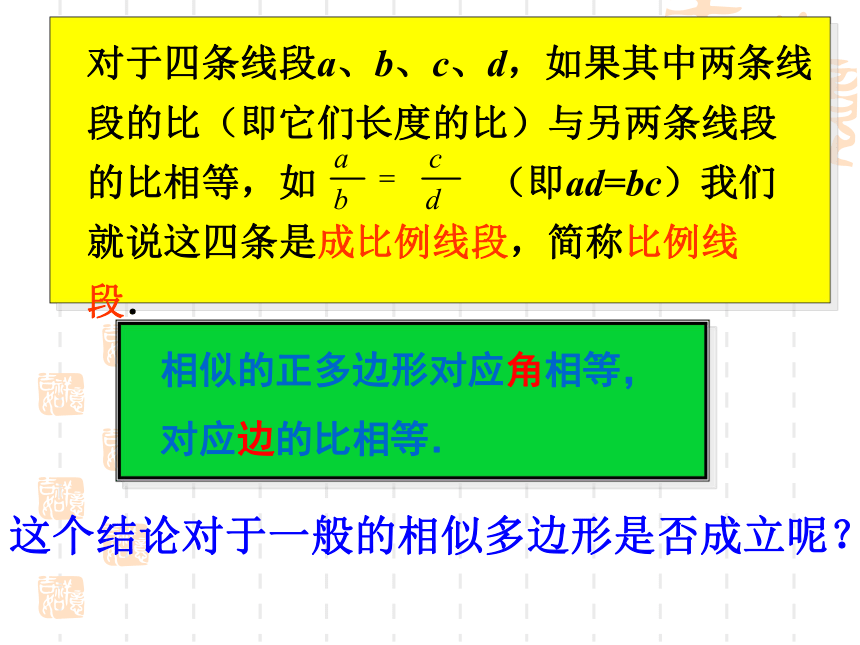
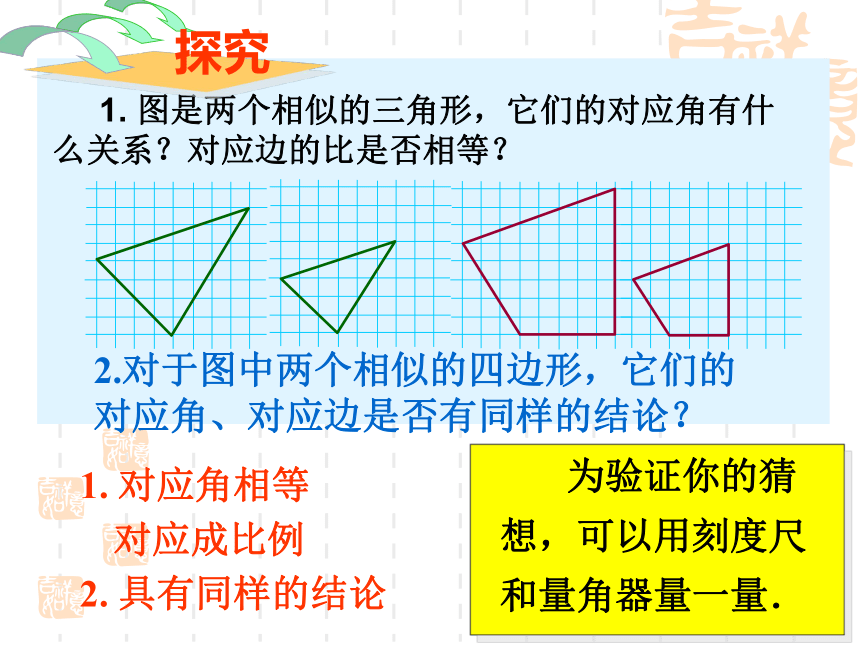
CABC1A1B1 对比图中的△A1B1C1和△ABC,由于正三角形的每个角都等于60 ° ,可得∠A=∠A1,∠B=∠B1,∠C=∠C1由△ABC和△A1B1C1是正三角形可得:AB=BC=AC, A1B1=B1C1=A1C1 这说明:正三角形都是相似的,它们的对应角相等,对应边的比相等.图中的两个相似的正六边形,也有类似的结论.对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条是成比例线段,简称比例线段.这个结论对于一般的相似多边形是否成立呢? 1. 图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?2.对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?1. 对应角相等对应成比例2. 具有同样的结论多边形相似特征: 如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.相似比: 我们把相似多边形对应边的比称为相似比.多边形相似的定义:相似比为1时,相似的两个图形有什么关系?两图形全等例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得 四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得解得 x=28(cm)∠α=∠D=83°,∠A=∠E=118°在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.1. 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离 练 习设两地的实际距离为xx = 300000000x = 3000千米答: 甲,乙两地的实际距离为30000千米解:2. 如图所示的两个三角形一定相似吗?为什么?105510 不一定不 相 似3. 如图所示的两个五边形相似,
求未知边a、b、c、d的长度.解:由图示: 可知两图形的相似比为:所以b = 4.5a = 3c = 4d = 6
CABC1A1B1 对比图中的△A1B1C1和△ABC,由于正三角形的每个角都等于60 ° ,可得∠A=∠A1,∠B=∠B1,∠C=∠C1由△ABC和△A1B1C1是正三角形可得:AB=BC=AC, A1B1=B1C1=A1C1 这说明:正三角形都是相似的,它们的对应角相等,对应边的比相等.图中的两个相似的正六边形,也有类似的结论.对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条是成比例线段,简称比例线段.这个结论对于一般的相似多边形是否成立呢? 1. 图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?2.对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?1. 对应角相等对应成比例2. 具有同样的结论多边形相似特征: 如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.相似比: 我们把相似多边形对应边的比称为相似比.多边形相似的定义:相似比为1时,相似的两个图形有什么关系?两图形全等例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得 四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得解得 x=28(cm)∠α=∠D=83°,∠A=∠E=118°在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.1. 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离 练 习设两地的实际距离为xx = 300000000x = 3000千米答: 甲,乙两地的实际距离为30000千米解:2. 如图所示的两个三角形一定相似吗?为什么?105510 不一定不 相 似3. 如图所示的两个五边形相似,
求未知边a、b、c、d的长度.解:由图示: 可知两图形的相似比为:所以b = 4.5a = 3c = 4d = 6
