26.1.2 反比例函数的图象与性质
文档属性
| 名称 | 26.1.2 反比例函数的图象与性质 |  | |
| 格式 | zip | ||
| 文件大小 | 862.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-22 14:45:22 | ||
图片预览







文档简介
课件26张PPT。第1课时26.1.2 反比例函数的图象与性质1.进一步熟悉作函数图象的步骤,会画反比例函数的图象.
2.体会函数的三种表示方法的相互转换,逐步提高从函数图象获取信息的能力,探索并掌握反比例函数的主要性质.1.什么是反比例函数?2.反比例函数的定义中需要注意什么?(1)k 是非零常数.(2)xy = k.一般地,形如 y = ( k是常数, k ≠0 )
的函数叫做反比例函数.(1).任意写一个在第二象限的点的坐标:_________.
(2).直线y=-x+3经过第___________象限.
(3).已知矩形的面积为6,则它的长y与宽x之间的函数关系
式为_____________,y 是x的__________函数.
(4).若函数y=2xm+1是反比例函数,则m=________.
(5).反比例函数 经过点(1,__).(-3,1)一、二、四-24反比例3.还记得一次函数的图像与性质吗?
4、还记得二次函数的图像与性质吗?
5、如何画函数的图像?
提问:反比例函数的图像与性质又如何呢?
这节课开始我们来一起探究吧。
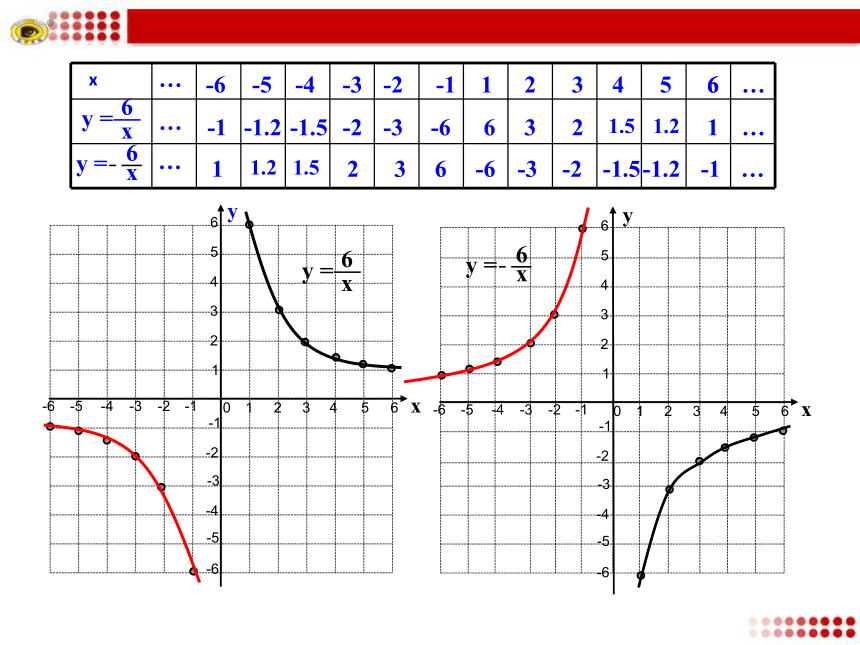
函数图象画法 描点法画出反比例函数 和
的函数图象. y =x6y = x6 函数图象画法 描点法123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……你认为作反比例函数图象时应注意哪些问题?1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
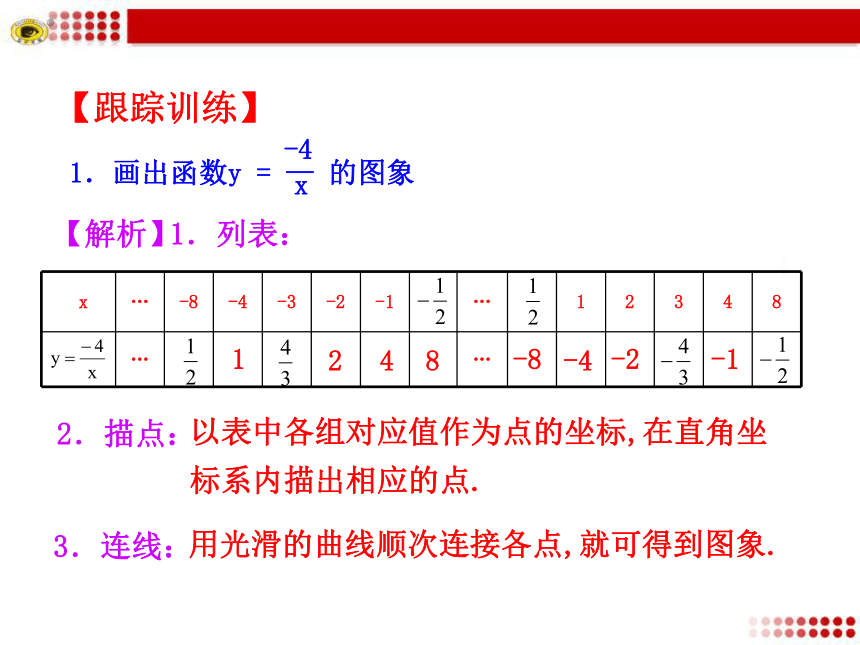
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.【解析】1.列表:2.描点:3.连线:-1-2-4-88421以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.用光滑的曲线顺次连接各点,就可得到图象.【跟踪训练】512346-4-1-2.-3-5-6124563-6-5-1-3-4-20... yx....-7-7-87 8.78...-8123456-4-1-2.-3-5-6124563-6-5-1-3-4-20..... yx ....y=— .xy0132456123456-6-6-5-3-4-1-2-4-5-3-2-1.........位置:
函数 的两支曲线分别位于第一、三象限内.
函数 的两支曲线分别位于第二、四象限内.形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线.【结论】反比例函数 的图象在哪两个象限,由什么确定?当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.答:由k的符号决定.K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线; 2.图象性质见下表:归纳:反比例函数的图象和性质:B.xyoD.xyo1.反比例函数y= - 的图象大致是( ) D2.如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内
的图象大致是( )D....3.已知反比例函数 的图象在
第二、四象限,那么一次函数y=kx-k的图象经过( )A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限C4.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽
车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)
的函数,则这个函数的图象大致是( )C提示:在实际问题中图象只有一支曲线.5.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_________.k>-16、已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.< 4> 4 7、考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-108、若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B 9、已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).C1.形状
反比例函数的图象是由两支曲线组成的,
因此称反比例函数的图象为双曲线.
2.位置
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.反比例函数的图象和性质K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
图象性质见下表:归纳:反比例函数的图象和性质:努力求学没有得到别的好处,只不过是愈来愈发觉自己的无知.
——佚名
2.体会函数的三种表示方法的相互转换,逐步提高从函数图象获取信息的能力,探索并掌握反比例函数的主要性质.1.什么是反比例函数?2.反比例函数的定义中需要注意什么?(1)k 是非零常数.(2)xy = k.一般地,形如 y = ( k是常数, k ≠0 )
的函数叫做反比例函数.(1).任意写一个在第二象限的点的坐标:_________.
(2).直线y=-x+3经过第___________象限.
(3).已知矩形的面积为6,则它的长y与宽x之间的函数关系
式为_____________,y 是x的__________函数.
(4).若函数y=2xm+1是反比例函数,则m=________.
(5).反比例函数 经过点(1,__).(-3,1)一、二、四-24反比例3.还记得一次函数的图像与性质吗?
4、还记得二次函数的图像与性质吗?
5、如何画函数的图像?
提问:反比例函数的图像与性质又如何呢?
这节课开始我们来一起探究吧。
函数图象画法 描点法画出反比例函数 和
的函数图象. y =x6y = x6 函数图象画法 描点法123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……你认为作反比例函数图象时应注意哪些问题?1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.【解析】1.列表:2.描点:3.连线:-1-2-4-88421以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.用光滑的曲线顺次连接各点,就可得到图象.【跟踪训练】512346-4-1-2.-3-5-6124563-6-5-1-3-4-20... yx....-7-7-87 8.78...-8123456-4-1-2.-3-5-6124563-6-5-1-3-4-20..... yx ....y=— .xy0132456123456-6-6-5-3-4-1-2-4-5-3-2-1.........位置:
函数 的两支曲线分别位于第一、三象限内.
函数 的两支曲线分别位于第二、四象限内.形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线.【结论】反比例函数 的图象在哪两个象限,由什么确定?当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.答:由k的符号决定.K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线; 2.图象性质见下表:归纳:反比例函数的图象和性质:B.xyoD.xyo1.反比例函数y= - 的图象大致是( ) D2.如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内
的图象大致是( )D....3.已知反比例函数 的图象在
第二、四象限,那么一次函数y=kx-k的图象经过( )A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限C4.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽
车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)
的函数,则这个函数的图象大致是( )C提示:在实际问题中图象只有一支曲线.5.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_________.k>-16、已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.< 4> 4 7、考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-1
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B 9、已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).C1.形状
反比例函数的图象是由两支曲线组成的,
因此称反比例函数的图象为双曲线.
2.位置
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.反比例函数的图象和性质K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
图象性质见下表:归纳:反比例函数的图象和性质:努力求学没有得到别的好处,只不过是愈来愈发觉自己的无知.
——佚名
