2.4解直角三角形 同步优生辅导训练题 2023-2024学年鲁教版(五四制)九年级数学上册(含答案)
文档属性
| 名称 | 2.4解直角三角形 同步优生辅导训练题 2023-2024学年鲁教版(五四制)九年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 482.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 15:08:39 | ||
图片预览


文档简介
2023-2024学年鲁教版九年级数学上册《2.4解直角三角形》同步优生辅导训练题(附答案)
一.选择题
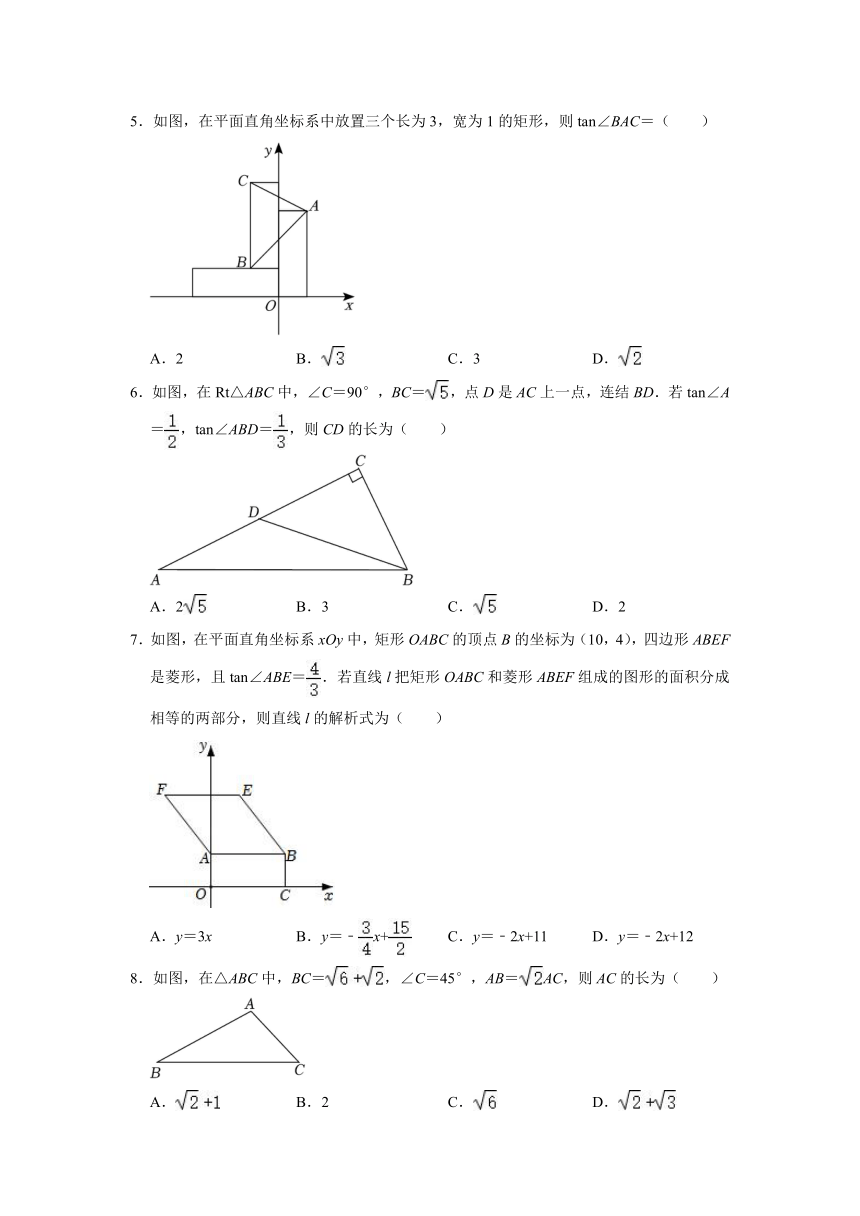
1.如图,在△ABC中,∠ACB=60°,∠B=45°,AB=,CE平分∠ACB交AB于点E,则线段CE的长为( )
A.+1 B.2 C. D.﹣
2.如图,在Rt△ABC中,ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,sin∠CEF=,则△AEF的面积为( )
A.3 B.4 C.5 D.6
3.如图是小夏同学家的衣架示意图.已知AB=AC=18cm,∠B=α,则衣架的宽BC为( )
A.36sinαcm B.36cosαcm C.18tanαcm D.cm
4.如图,边长为1的小正方形网格中,点A、B、C、E在格点上,连接AE、BC,点D在BC上且满足AD⊥BC,则∠AED的正切值是( )
A. B.2 C. D.
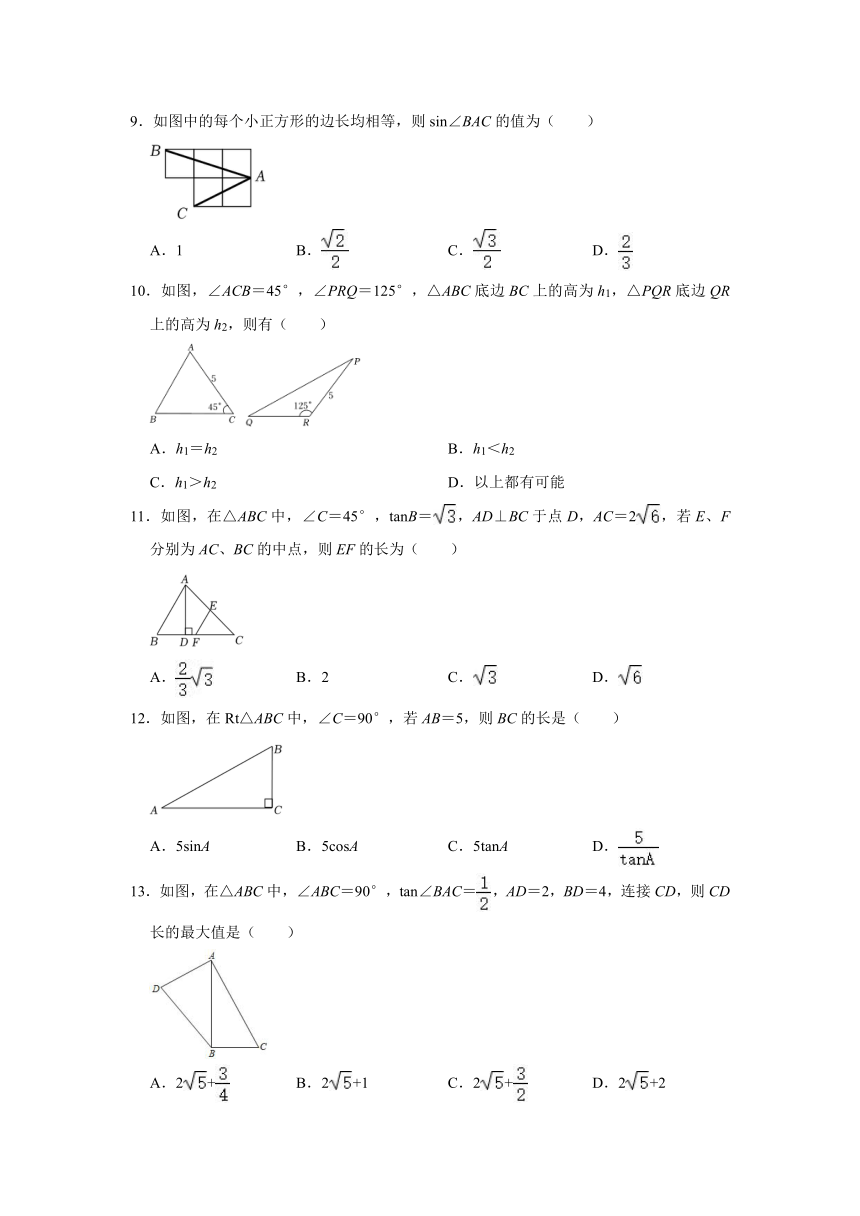
5.如图,在平面直角坐标系中放置三个长为3,宽为1的矩形,则tan∠BAC=( )
A.2 B. C.3 D.
6.如图,在Rt△ABC中,∠C=90°,BC=,点D是AC上一点,连结BD.若tan∠A=,tan∠ABD=,则CD的长为( )
A.2 B.3 C. D.2
7.如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A.y=3x B.y=﹣x+ C.y=﹣2x+11 D.y=﹣2x+12
8.如图,在△ABC中,BC=,∠C=45°,AB=AC,则AC的长为( )
A. B.2 C. D.
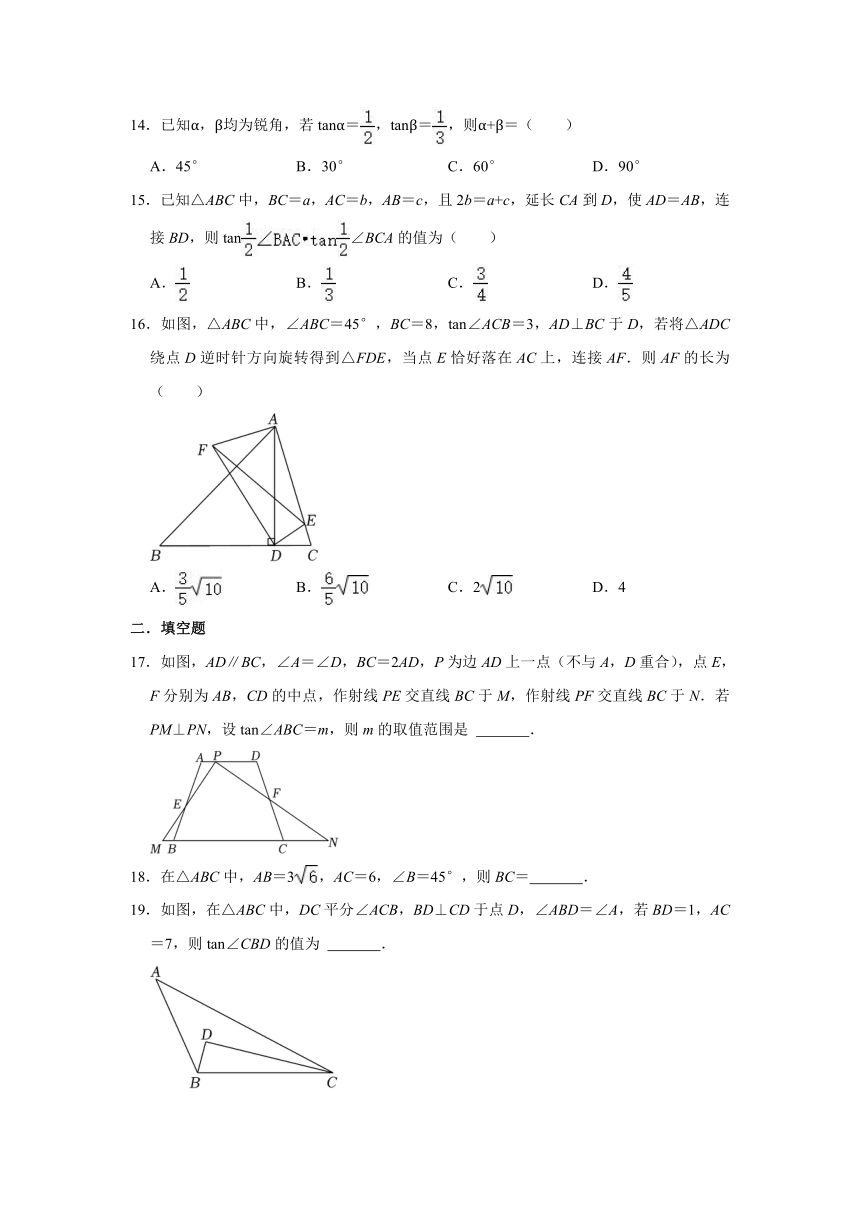
9.如图中的每个小正方形的边长均相等,则sin∠BAC的值为( )
A.1 B. C. D.
10.如图,∠ACB=45°,∠PRQ=125°,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
11.如图,在△ABC中,∠C=45°,tanB=,AD⊥BC于点D,AC=2,若E、F分别为AC、BC的中点,则EF的长为( )
A. B.2 C. D.
12.如图,在Rt△ABC中,∠C=90°,若AB=5,则BC的长是( )
A.5sinA B.5cosA C.5tanA D.
13.如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A.2+ B.2+1 C.2+ D.2+2
14.已知α,β均为锐角,若tanα=,tanβ=,则α+β=( )
A.45° B.30° C.60° D.90°
15.已知△ABC中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB,连接BD,则tan∠BCA的值为( )
A. B. C. D.
16.如图,△ABC中,∠ABC=45°,BC=8,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )
A. B. C.2 D.4
二.填空题
17.如图,AD∥BC,∠A=∠D,BC=2AD,P为边AD上一点(不与A,D重合),点E,F分别为AB,CD的中点,作射线PE交直线BC于M,作射线PF交直线BC于N.若PM⊥PN,设tan∠ABC=m,则m的取值范围是 .
18.在△ABC中,AB=3,AC=6,∠B=45°,则BC= .
19.如图,在△ABC中,DC平分∠ACB,BD⊥CD于点D,∠ABD=∠A,若BD=1,AC=7,则tan∠CBD的值为 .
20.如图,在正方形网格中,四边形ABCD的顶点均在格点上,对角线AC交BD于点E,则tan∠CED的值是 .
21.△ABC中,,,,则BC边的长为 .
22.如图,△ABC的顶点都在正方形网格纸的格点上,则sin= .
23.如图,已知点A(4,3),点B为直线y=﹣2上的一动点,点C(0,n),﹣2<n<3,AC⊥BC于点C,连接AB.若直线AB与x轴正半轴所夹的锐角为α,那么当sinα的值最大时,n的值为 .
三.解答题
24.阅读材料:关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ,tan(α+β)=.利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和(差),如tan75°=tan(30°+45°)==2+.
问题解决:根据以上阅读材料,请选择适当的公式解答下列问题.
(1)求sin75°;
(2)如图,边长为2的正△ABC沿直线滚动,设当△ABC滚动240°时,C点的位置在C′,当△ABC滚动480°时,A点的位置在A′.
①求tan∠CAC′的值;
②试确定∠CAC′+∠CAA′的度数.
25.如图(1),由直角三角形边角关系,可将三角形面积公式变形得到…①
即三角形的面积等于两边之长与夹角正弦值之积的一半
如图,在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β
∵S△ABC=S△ACD+S△BCD,由公式①得到
即AC BC sin(α+β)=AC CD sinα+BC CD sinβ…②
你能利用直角三角形关系及等式基本性质,消去②中的AC、BC、CD吗?若不能,说明理由;若能,写出解决过程.并利用结论求出sin75°的值.
26.对于钝角α,定义它的三角函数值如下:sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α).
(1)求sin120°,cos150°的值;
(2)若一个钝角三角形的三个内角比是1:1:4,A,B设这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
27.在一节数学实践课上,老师出示了这样一道题,如图1,在锐角三角形ABC中,∠A、∠B、∠C所对边分别是a、b、c,请用a、c、∠B表示b2.
经过同学们的思考后,
甲同学说:要将锐角三角形转化为直角三角形来解决,并且不能破坏∠B,因此可以经过点A,作AD⊥BC于点D,如图2,大家认同;
乙同学说要想得到b2要在Rt△ABD或Rt△ACD中解决;
丙同学说那就要先求出AD= ,BD= ;(用含c,∠B的三角函数表示)
丁同学顺着他们的思路,求出b2=AD2+DC2= (其中sin2α+cos2α=1);请利用丁同学的结论解决如下问题:
如图3,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,AB=4,AD=5.
求AC的长(补全图形,直接写出结果即可).
28.如图,在△ABC中,∠ABC=90°,AB=,BC=1,点P为△ABC内一点,∠BPC=90°.
(1)若PB=,求线段PA的长;
(2)若tan∠PBA=,求∠APB的度数.
29.阅读下面的材料:某数学学习小组遇到这样一个问题:
如果α,β都为锐角,且tanα=,tanβ=,求α+β的度数.
该数学课外小组最后是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC.
(1)观察图象可知:α+β= °;
(2)请参考该数学小组的方法解决问题:如果α,β都为锐角,当tanα=3,tanβ=时,在图2的正方形网格中,画出∠MON=α﹣β,并求∠MON的度数.
参考答案
一.选择题
1.解:如图,
作AD⊥BC于D,作EF⊥BC于F,
在Rt△ABD中,
BD=AD=AB sinB=×=,
在Rt△ADC中,∠DAC=90°﹣∠ACB=30°,
CD=AD tan30°=×=1,
∴BC=+1,
在Rt△BEF中,设BF=EF=x,
在Rt△EFC中,∠FEC=90°﹣∠BCE=60°,
CF=EF tan60°=x,
由CF+BF=BC得,
,
∴x=1,
∴EC=2EF=2,
故答案为:B.
2.解:过点C作CD⊥AB,垂足为D,
∵EF⊥AB,
∴CD∥EF,
∴∠DCE=∠CEF,
在Rt△CDE中,sin∠DCE=sin∠CEF==,
设DE=3x,则CE=5x,
∴CD==4x,
在Rt△ABC中,BE=EA,
∴CE=BE=EA=5x,
∴AB=2BE=10x,
∴BD=BE﹣DE=2x,
在Rt△BCD中,BC2=BD2+CD2,BC=4,
∴42=(4x)2+(2x)2
∴x=,
∵Rt∠CDA=Rt∠FEA,∠A=∠A,
∴△ACD∽△AFE,
∴
∴,
∴EF=,
∵AE=5x=2,
∴
=
=5.
故选:C.
3.解:如图,过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BC=2BD.
∵AD⊥BC,
∴BD=ABcosα.
∴BC=2BD=2ABcosα=36cosα(cm).
故选:B.
4.解:连接OD,
∵AD⊥BC,O是AB中点,
∴OD=AB=1,
∴OD=OA=OE=OD,
∴点A、D、B、E在以O为圆心,1为半径的同一个圆上,
∴∠ABC=∠AED,
∴tan∠AED=tan∠ABD=,
故选:A.
5.解:如图,过C作CE⊥AB于E,延长AF交BC于D,
依题意BC=3,AD=BD=2,CD=1,
在Rt△ADC中,AC==,
在Rt△ADB中,AB==2,
∵S△ABC=AD×BC=CE×AB,
∴CE=,
∴AE==,
∴tan∠BAC==3.
故选:C.
6.解:过D点作DE⊥AB于E,
∵tan∠A==,tan∠ABD==,
∴AE=2DE,BE=3DE,
∴2DE+3DE=5DE=AB,
在Rt△ABC中,tan∠A=,BC=,
∴,
解得AC=,
∴AB=,
∴DE=1,
∴AE=2,
∴AD=,
∴CD=AC﹣AD=,
故选:C.
7.解:连接OB,AC,它们交于点M,连接AE,BF,它们交于点N,
则直线MN为符合条件的直线l,如图,
∵四边形OABC是矩形,
∴OM=BM.
∵B的坐标为(10,4),
∴M(5,2),AB=10,BC=4.
∵四边形ABEF为菱形,
BE=AB=10.
过点E作EG⊥AB于点G,
在Rt△BEG中,
∵tan∠ABE=,
∴,
设EG=4k,则BG=3k,
∴BE==5k,
∴5k=10,
∴k=2,
∴EG=8,BG=6,
∴AG=4.
∴E(4,12).
∵B的坐标为(10,4),AB∥x轴,
∴A(0,4).
∵点N为AE的中点,
∴N(2,8).
设直线l的解析式为y=ax+b,
∴,
解得:,
∴直线l的解析式为y=﹣2x+12,
故选:D.
8.解:过点A作AD⊥BC,垂足为D,
在Rt△ADC中,∠C=45°,
∴AD=DC,AC=AD,
∵AB=AC,
∴AB=2AD,
在Rt△ABD中,AB=2AD,
∴∠B=30°,
∴BD=AD,
∵BC=,
∴BD+CD=+,
∴AD+AD=+,
∴AD=,
∴AC=AD=2,
故选:B.
9.解:连接BC,
由题意得:
BC2=12+22=5,
AC2=12+22=5,
AB2=12+32=10,
∴BC2+AC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°,
∵AC=BC,
∴∠BAC=∠ABC=45°,
∴sin∠BAC=sin45°=,
故选:B.
10.解:过点A作AE⊥BC,垂足为E,过点P作PF⊥QR,交QR的延长线于点F,
在Rt△AEC中,AC=5,∠C=45°,
∴h1=AE=ACsin45°=5sin45°,
∵∠PRQ=125°,
∴∠PRF=180°﹣∠PRQ=180°﹣125°=55°,
在Rt△PRF中,h2=PF=PRsin55°=5sin55°,
∴h1<h2,
故选:B.
11.解:在Rt△ACD中,AC=2,∠C=45°,
∴AD=ACsin45°=2×=2,
∵tanB=,
∴∠B=60°,
在Rt△ABD中,AB===4,
∵E、F分别为AC、BC的中点,
∴EF是△ABC的中位线,
∴EF=AB=2,
故选:B.
12.解:在Rt△ABC中,∠C=90°,AB=5,
∴sinA=,
∴BC=ABsinA=5sinA,
故选:A.
13.解:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,
∵==2,
∴=,
∵∠ADT=∠ABC=90°,
∴△ADT∽△ABC,
∴∠DAT=∠BAC,=
∴∠DAB=∠TAC,
∵=,
∴△DAB∽△TAC,
∴==,
∴TC=2,
∵CD≤DT+CT,
∴CD≤1+2,
∴CD的最大值为1+2,
故选:B.
14.解:如图△ABC,过点A作AD⊥BC,
设:BD=3a,CD=2a,AD=6a,
则tanα=tan∠BAD==,同理tan,
则AB=,AC=,
过点B作BE⊥AC于点E,
S△ABC=AD×BC=×AC×BE,
即5a 6a=BE,解得:BE=,
sin(α+β)=sin∠BAC===,
则α+β=45°,
故选:A.
15.解:过点B作BH⊥AC于H,
设HC=x,HA=y,HB=h,
∴x2+h2=a2,y2+h2=c2,x+y=b.
解得:x=(5a﹣3c),y=(5c﹣3a),h=(3c﹣a)(3a﹣c).
∵CE=CB,
∴∠E=∠CBE,
∵∠BCA=∠CBE+∠E,
∴∠E=∠BCA,
∴tan∠BAC tan∠BCA=tan∠D tan∠E====.
故选:B.
16.解:过点D作DH⊥AF于点H,
∵∠ABC=45°,AD⊥BC,
∴AD=BD,
∵tan∠ACB==3,
设CD=x,
∴AD=3x,
∴BC=3x+x=8,
∴x=2,
∴CD=2,AD=6,
∴AC=,
∵将△ADC绕点D逆时针方向旋转得到△FDE,
∴DC=DE,DA=DF=6,∠CDE=∠ADF,
∴∠DCE=∠DAF,
∴tan∠DAH=3,
设AH=a,DH=3a,
∵AH2+DH2=AD2,
∴a2+(3a)2=62,
∴a=,
∴AH=,
∴AF=2AH=.
故选:B.
二.填空题
17.解:如图,取MN的中点H,连接PH,过点P作PQ⊥BC于Q,过点A作AG⊥BC于G,过点D作DK⊥BC于K,则AG=DK,
∵AD∥BC,
∴∠DAB+∠ABC=180°,∠ADC=∠DCB=180°,
∵∠DAB=∠ADC,
∴∠ABC=∠DCB,
∵∠AGB=∠DKC=90°,
∴△ABG≌△DCK(AAS),
∴AB=CD,BG=CK,
∵E是AB的中点,
∴AE=BE,
∵∠AEP=∠BEM,∠PAE=∠EBM,
∴△PAE≌△MBE(ASA),
∴AP=BM,
同理得:PD=CN,
∵AD=KG,BC=2AD,
∴MN=3AD,
∵PM⊥PN,
∴∠MPN=90°,
∵H是MN的中点,
∴PH=MN,
设BC=2AD=4k,AP=GQ=MB=a,则BG=k,MN=6k,PH=3k,
∵tan∠ABC==m,
∴PQ=AG=km,
∵PQ2=PH2﹣QH2,
即k2m2=9k2﹣(2k﹣2a)2,
∴m2=﹣++5=﹣(a﹣k)2+9,
又∵0<a<2k,
当a=0时,m2=5,
当a=k时,Q与H重合,不符合题意,
∴5<m2<9,
∴<m<3.
故答案为:<m<3.
18.解:①当△ABC为锐角三角形时,
过点A作AD⊥BC于点D,如图,
∵AB=3,∠B=45°,
∴AD=BD=AB sin45°=3,
∴CD==3,
∴BC=BD+CD=3+3;
②当△ABC为钝角三角形时,
过点A作AD⊥BC交BC延长线于点D,如图,
∵AB=3,∠B=45°,
∴AD=BD=AB sin45°=3,
∴CD==3,
∴BC=BD﹣CD=3﹣3;
综上,BC的长为3+3或3﹣3.
19.解:延长BD交AC于点E.
∵DC平分∠ACB,BD⊥CD于点D,
∴∠CDE=∠CDB=90°,∠DCE=∠DCB.
在△DCE和△DCB中,
,
∴△DCE≌△DCB(SAS).
∴BD=ED=1.
∵∠ABD=∠A,
∴AE=BE=2.
∵AC=7,
∴CE=AC﹣AE=5.
∴CD=
=
=2.
∴tan∠CBD===2.
故答案为:2.
20.解:设小正方形的边长为1,则AD=5,BC=4,
∵AD∥BC,
∴===,
由勾股定理得:BD==,DC==,AC==2,
则DE=BD=,CE=AC=,
过C作CF⊥BD于F,
∵△BCD的面积S=4×2=4,
∴△DCE的面积为×4=,
∴CF=,
∴××CF=,
∴CF=,
由勾股定理得:EF===,
∴tan∠CED===,
故答案为:.
21.解:如图所示,当∠C为钝角时,过点A作AD⊥BC,交BC的延长线于点D.
在Rt△ABD中,
∵AB=2,=,
∴AD=2.
∴BD==2.
在Rt△ACD中,
CD==1.
∴BC=BD﹣CD=1.
如图所示,当∠C为锐角时,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,
∵AB=2,=,
∴AD=2.
∴BD==2.
在Rt△ACD中,
CD==1.
∴BC=BD+CD=3.
故答案为:1或3.
22.解:如图,取格点T,连接AT,BT,设BT的中点为H,连接CH.
∵BC==5,CT==5,
∴CB=CT,
∵BH=HT,
∴∠HCA=∠HCB,CH⊥BT,
∵HT=,
∴sin===,
故答案为:.
23.解:过点A作AM⊥y轴于点M,作AN⊥BN交于点N,
∵直线y=﹣2与x轴平行,
∴∠ABN=α,
当sinα的值最大时,则tanα=值最大,
故BN最小,即BG最大时,tanα最大,
即当BG最大时,sinα的值最大,
设BG=m,
则AM=4,GC=n+2,CM=3﹣n,
∵∠ACM+∠MAC=90°,∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
∴tan∠CAM=tan∠BCG,
∴,即=,
∴m=﹣(n﹣3)(n+2)=﹣(n﹣)2+,
∵﹣<0,
∴当n=时,m取得最大值,
故n=,
故答案为:.
三.解答题
24.解:(1)sin75°=sin(30°+45°)
=sin30° cos45°+cos30° sin45°
=+
=;
(2)①过C′作C′E⊥l于E,
∵△ABC是等边三角形且边长为2,
∴C′E=,AE=2+2+1=5,
∴tan∠CAC′==;
②过A′作A′F⊥l于F,
∵△ABC是等边三角形且边长为2,
∴A′F=,AF=2+2+2+2+1=9,
∴tan∠CAA′==.
设∠CAC′=α,∠CAA′=β,
tan(α+β)===,
∴α+β=30°,
∴∠CAC′+CAA′=30°.
25.解:①能消去②中的AC、BC、CD.
将AC BC sin(α+β)=AC CD sinα+BC CD sinβ,两边同除以AC BC得:
sin(α+β)= sinα+ sinβ③,
又∵cosβ=、cosα=,
代入③可得:sin(α+β)=sinα cosβ+cosα sinβ.
②由sin(α+β)=sinα cosβ+cosα sinβ得:sin75°=sin(30°+45°)=sin30° cos45°+cos30° sin45°
=×+×
=.
26.解:(1)由题意得:sin120°=sin(180°﹣120°)=sin60°=,cos150°=cos(180°﹣30°)=﹣cos30°=﹣;
(2)∵一个钝角三角形的三个内角比是1:1:4,
∴三个内角分别为30°,30°,120°,
①当∠A=30°,∠B=120°时,方程的两根为,﹣,
把代入方程得:1﹣m﹣1=0,解得:m=0,
经检验﹣是4x2﹣1=0的根,故m=0;
②当∠A=120°,∠B=30°时,方程的两根为,,不符合题意;
③∠A=30°,∠B=30°时,方程两根为,,
把代入得:1﹣m﹣1=0,解得:m=0,
经检验不是方程4x2﹣1=0的根,不符合题意,
则m=0,∠A=30°,∠B=120°.
27.解:∵sinB=,cosB=,
∴AD=AB sinB=c sinB,BD=AB cosB=c cosB,
CD=BC﹣BD=a﹣c cosB,
则出b2=AD2+DC2=(c sinB)2+(a﹣c cosB)2
=c2sin2B+a2+c2cos2B+2ac cosB
=c2(sin2B+cos2B)+a2﹣2ac cosB
=a2+c2﹣2ac cosB.
如图3所示,延长BC,AD交于E,
∵∠B=90°,∠BAD=60°,AB=4,
∴AE=2AB=8,∠E=30°,
∵AD=5,
∴DE=3,
∵∠ADC=∠CDE=90°,
∴CE=2,
∴AC2=CE2+AE2﹣2CE AEcos30°=12+64﹣2××8×=28,
∴AC=2.
故答案是:c sinB,c cosB;a2+c2﹣2ac cosB.
28.解:(1)如图,过点P作PH⊥AB于H.
∵∠BPC=90°,PB=,BC=1,
∴cos∠CBP==,
∴∠CBP=60°,
∵∠ABC=90°,
∴∠PBH=90°﹣60°=30°,
∴PH=PB=,BH=PH=,
∵AB=,
∴AH=AB﹣BH=,
∴AP==.
(2)如图,过点A作AT⊥BP交BP的延长线于T.
∵tan∠TBA==,AB=,
∴AT=,BT=,
∵∠BCP+∠CBP=90°,∠CBP+∠ABP=90°,
∴∠BCP=∠ABP,
∴tan∠CBP=,
∵BC=1,
∴PB=,
∴PT=BT﹣PB=,
∴tan∠APT==,
∴∠APT=60°,
∴∠APB=120°.
29.解:(1)如图1.
∵BC2=32+52=34,AB2=42+12=17,AC2=42+12=17,
∴BC2=AB2+AC2=2AB2,
∴△ABC是等腰直角三角形,且∠BAC=90°,
∴α+β=∠ABC=45°.
故答案为45;
(2)如图2,连接MN.
∵OM2=32+12=10,ON2=22+12=5,MN2=22+12=5,
∴OM2=ON2+MN2=2ON2,
∴△OMN是等腰直角三角形,且∠ONM=90°,
∴α﹣β=∠MON=45°
一.选择题
1.如图,在△ABC中,∠ACB=60°,∠B=45°,AB=,CE平分∠ACB交AB于点E,则线段CE的长为( )
A.+1 B.2 C. D.﹣
2.如图,在Rt△ABC中,ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,sin∠CEF=,则△AEF的面积为( )
A.3 B.4 C.5 D.6
3.如图是小夏同学家的衣架示意图.已知AB=AC=18cm,∠B=α,则衣架的宽BC为( )
A.36sinαcm B.36cosαcm C.18tanαcm D.cm
4.如图,边长为1的小正方形网格中,点A、B、C、E在格点上,连接AE、BC,点D在BC上且满足AD⊥BC,则∠AED的正切值是( )
A. B.2 C. D.
5.如图,在平面直角坐标系中放置三个长为3,宽为1的矩形,则tan∠BAC=( )
A.2 B. C.3 D.
6.如图,在Rt△ABC中,∠C=90°,BC=,点D是AC上一点,连结BD.若tan∠A=,tan∠ABD=,则CD的长为( )
A.2 B.3 C. D.2
7.如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A.y=3x B.y=﹣x+ C.y=﹣2x+11 D.y=﹣2x+12
8.如图,在△ABC中,BC=,∠C=45°,AB=AC,则AC的长为( )
A. B.2 C. D.
9.如图中的每个小正方形的边长均相等,则sin∠BAC的值为( )
A.1 B. C. D.
10.如图,∠ACB=45°,∠PRQ=125°,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
11.如图,在△ABC中,∠C=45°,tanB=,AD⊥BC于点D,AC=2,若E、F分别为AC、BC的中点,则EF的长为( )
A. B.2 C. D.
12.如图,在Rt△ABC中,∠C=90°,若AB=5,则BC的长是( )
A.5sinA B.5cosA C.5tanA D.
13.如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A.2+ B.2+1 C.2+ D.2+2
14.已知α,β均为锐角,若tanα=,tanβ=,则α+β=( )
A.45° B.30° C.60° D.90°
15.已知△ABC中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB,连接BD,则tan∠BCA的值为( )
A. B. C. D.
16.如图,△ABC中,∠ABC=45°,BC=8,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )
A. B. C.2 D.4
二.填空题
17.如图,AD∥BC,∠A=∠D,BC=2AD,P为边AD上一点(不与A,D重合),点E,F分别为AB,CD的中点,作射线PE交直线BC于M,作射线PF交直线BC于N.若PM⊥PN,设tan∠ABC=m,则m的取值范围是 .
18.在△ABC中,AB=3,AC=6,∠B=45°,则BC= .
19.如图,在△ABC中,DC平分∠ACB,BD⊥CD于点D,∠ABD=∠A,若BD=1,AC=7,则tan∠CBD的值为 .
20.如图,在正方形网格中,四边形ABCD的顶点均在格点上,对角线AC交BD于点E,则tan∠CED的值是 .
21.△ABC中,,,,则BC边的长为 .
22.如图,△ABC的顶点都在正方形网格纸的格点上,则sin= .
23.如图,已知点A(4,3),点B为直线y=﹣2上的一动点,点C(0,n),﹣2<n<3,AC⊥BC于点C,连接AB.若直线AB与x轴正半轴所夹的锐角为α,那么当sinα的值最大时,n的值为 .
三.解答题
24.阅读材料:关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ,tan(α+β)=.利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和(差),如tan75°=tan(30°+45°)==2+.
问题解决:根据以上阅读材料,请选择适当的公式解答下列问题.
(1)求sin75°;
(2)如图,边长为2的正△ABC沿直线滚动,设当△ABC滚动240°时,C点的位置在C′,当△ABC滚动480°时,A点的位置在A′.
①求tan∠CAC′的值;
②试确定∠CAC′+∠CAA′的度数.
25.如图(1),由直角三角形边角关系,可将三角形面积公式变形得到…①
即三角形的面积等于两边之长与夹角正弦值之积的一半
如图,在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β
∵S△ABC=S△ACD+S△BCD,由公式①得到
即AC BC sin(α+β)=AC CD sinα+BC CD sinβ…②
你能利用直角三角形关系及等式基本性质,消去②中的AC、BC、CD吗?若不能,说明理由;若能,写出解决过程.并利用结论求出sin75°的值.
26.对于钝角α,定义它的三角函数值如下:sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α).
(1)求sin120°,cos150°的值;
(2)若一个钝角三角形的三个内角比是1:1:4,A,B设这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
27.在一节数学实践课上,老师出示了这样一道题,如图1,在锐角三角形ABC中,∠A、∠B、∠C所对边分别是a、b、c,请用a、c、∠B表示b2.
经过同学们的思考后,
甲同学说:要将锐角三角形转化为直角三角形来解决,并且不能破坏∠B,因此可以经过点A,作AD⊥BC于点D,如图2,大家认同;
乙同学说要想得到b2要在Rt△ABD或Rt△ACD中解决;
丙同学说那就要先求出AD= ,BD= ;(用含c,∠B的三角函数表示)
丁同学顺着他们的思路,求出b2=AD2+DC2= (其中sin2α+cos2α=1);请利用丁同学的结论解决如下问题:
如图3,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,AB=4,AD=5.
求AC的长(补全图形,直接写出结果即可).
28.如图,在△ABC中,∠ABC=90°,AB=,BC=1,点P为△ABC内一点,∠BPC=90°.
(1)若PB=,求线段PA的长;
(2)若tan∠PBA=,求∠APB的度数.
29.阅读下面的材料:某数学学习小组遇到这样一个问题:
如果α,β都为锐角,且tanα=,tanβ=,求α+β的度数.
该数学课外小组最后是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC.
(1)观察图象可知:α+β= °;
(2)请参考该数学小组的方法解决问题:如果α,β都为锐角,当tanα=3,tanβ=时,在图2的正方形网格中,画出∠MON=α﹣β,并求∠MON的度数.
参考答案
一.选择题
1.解:如图,
作AD⊥BC于D,作EF⊥BC于F,
在Rt△ABD中,
BD=AD=AB sinB=×=,
在Rt△ADC中,∠DAC=90°﹣∠ACB=30°,
CD=AD tan30°=×=1,
∴BC=+1,
在Rt△BEF中,设BF=EF=x,
在Rt△EFC中,∠FEC=90°﹣∠BCE=60°,
CF=EF tan60°=x,
由CF+BF=BC得,
,
∴x=1,
∴EC=2EF=2,
故答案为:B.
2.解:过点C作CD⊥AB,垂足为D,
∵EF⊥AB,
∴CD∥EF,
∴∠DCE=∠CEF,
在Rt△CDE中,sin∠DCE=sin∠CEF==,
设DE=3x,则CE=5x,
∴CD==4x,
在Rt△ABC中,BE=EA,
∴CE=BE=EA=5x,
∴AB=2BE=10x,
∴BD=BE﹣DE=2x,
在Rt△BCD中,BC2=BD2+CD2,BC=4,
∴42=(4x)2+(2x)2
∴x=,
∵Rt∠CDA=Rt∠FEA,∠A=∠A,
∴△ACD∽△AFE,
∴
∴,
∴EF=,
∵AE=5x=2,
∴
=
=5.
故选:C.
3.解:如图,过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BC=2BD.
∵AD⊥BC,
∴BD=ABcosα.
∴BC=2BD=2ABcosα=36cosα(cm).
故选:B.
4.解:连接OD,
∵AD⊥BC,O是AB中点,
∴OD=AB=1,
∴OD=OA=OE=OD,
∴点A、D、B、E在以O为圆心,1为半径的同一个圆上,
∴∠ABC=∠AED,
∴tan∠AED=tan∠ABD=,
故选:A.
5.解:如图,过C作CE⊥AB于E,延长AF交BC于D,
依题意BC=3,AD=BD=2,CD=1,
在Rt△ADC中,AC==,
在Rt△ADB中,AB==2,
∵S△ABC=AD×BC=CE×AB,
∴CE=,
∴AE==,
∴tan∠BAC==3.
故选:C.
6.解:过D点作DE⊥AB于E,
∵tan∠A==,tan∠ABD==,
∴AE=2DE,BE=3DE,
∴2DE+3DE=5DE=AB,
在Rt△ABC中,tan∠A=,BC=,
∴,
解得AC=,
∴AB=,
∴DE=1,
∴AE=2,
∴AD=,
∴CD=AC﹣AD=,
故选:C.
7.解:连接OB,AC,它们交于点M,连接AE,BF,它们交于点N,
则直线MN为符合条件的直线l,如图,
∵四边形OABC是矩形,
∴OM=BM.
∵B的坐标为(10,4),
∴M(5,2),AB=10,BC=4.
∵四边形ABEF为菱形,
BE=AB=10.
过点E作EG⊥AB于点G,
在Rt△BEG中,
∵tan∠ABE=,
∴,
设EG=4k,则BG=3k,
∴BE==5k,
∴5k=10,
∴k=2,
∴EG=8,BG=6,
∴AG=4.
∴E(4,12).
∵B的坐标为(10,4),AB∥x轴,
∴A(0,4).
∵点N为AE的中点,
∴N(2,8).
设直线l的解析式为y=ax+b,
∴,
解得:,
∴直线l的解析式为y=﹣2x+12,
故选:D.
8.解:过点A作AD⊥BC,垂足为D,
在Rt△ADC中,∠C=45°,
∴AD=DC,AC=AD,
∵AB=AC,
∴AB=2AD,
在Rt△ABD中,AB=2AD,
∴∠B=30°,
∴BD=AD,
∵BC=,
∴BD+CD=+,
∴AD+AD=+,
∴AD=,
∴AC=AD=2,
故选:B.
9.解:连接BC,
由题意得:
BC2=12+22=5,
AC2=12+22=5,
AB2=12+32=10,
∴BC2+AC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°,
∵AC=BC,
∴∠BAC=∠ABC=45°,
∴sin∠BAC=sin45°=,
故选:B.
10.解:过点A作AE⊥BC,垂足为E,过点P作PF⊥QR,交QR的延长线于点F,
在Rt△AEC中,AC=5,∠C=45°,
∴h1=AE=ACsin45°=5sin45°,
∵∠PRQ=125°,
∴∠PRF=180°﹣∠PRQ=180°﹣125°=55°,
在Rt△PRF中,h2=PF=PRsin55°=5sin55°,
∴h1<h2,
故选:B.
11.解:在Rt△ACD中,AC=2,∠C=45°,
∴AD=ACsin45°=2×=2,
∵tanB=,
∴∠B=60°,
在Rt△ABD中,AB===4,
∵E、F分别为AC、BC的中点,
∴EF是△ABC的中位线,
∴EF=AB=2,
故选:B.
12.解:在Rt△ABC中,∠C=90°,AB=5,
∴sinA=,
∴BC=ABsinA=5sinA,
故选:A.
13.解:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,
∵==2,
∴=,
∵∠ADT=∠ABC=90°,
∴△ADT∽△ABC,
∴∠DAT=∠BAC,=
∴∠DAB=∠TAC,
∵=,
∴△DAB∽△TAC,
∴==,
∴TC=2,
∵CD≤DT+CT,
∴CD≤1+2,
∴CD的最大值为1+2,
故选:B.
14.解:如图△ABC,过点A作AD⊥BC,
设:BD=3a,CD=2a,AD=6a,
则tanα=tan∠BAD==,同理tan,
则AB=,AC=,
过点B作BE⊥AC于点E,
S△ABC=AD×BC=×AC×BE,
即5a 6a=BE,解得:BE=,
sin(α+β)=sin∠BAC===,
则α+β=45°,
故选:A.
15.解:过点B作BH⊥AC于H,
设HC=x,HA=y,HB=h,
∴x2+h2=a2,y2+h2=c2,x+y=b.
解得:x=(5a﹣3c),y=(5c﹣3a),h=(3c﹣a)(3a﹣c).
∵CE=CB,
∴∠E=∠CBE,
∵∠BCA=∠CBE+∠E,
∴∠E=∠BCA,
∴tan∠BAC tan∠BCA=tan∠D tan∠E====.
故选:B.
16.解:过点D作DH⊥AF于点H,
∵∠ABC=45°,AD⊥BC,
∴AD=BD,
∵tan∠ACB==3,
设CD=x,
∴AD=3x,
∴BC=3x+x=8,
∴x=2,
∴CD=2,AD=6,
∴AC=,
∵将△ADC绕点D逆时针方向旋转得到△FDE,
∴DC=DE,DA=DF=6,∠CDE=∠ADF,
∴∠DCE=∠DAF,
∴tan∠DAH=3,
设AH=a,DH=3a,
∵AH2+DH2=AD2,
∴a2+(3a)2=62,
∴a=,
∴AH=,
∴AF=2AH=.
故选:B.
二.填空题
17.解:如图,取MN的中点H,连接PH,过点P作PQ⊥BC于Q,过点A作AG⊥BC于G,过点D作DK⊥BC于K,则AG=DK,
∵AD∥BC,
∴∠DAB+∠ABC=180°,∠ADC=∠DCB=180°,
∵∠DAB=∠ADC,
∴∠ABC=∠DCB,
∵∠AGB=∠DKC=90°,
∴△ABG≌△DCK(AAS),
∴AB=CD,BG=CK,
∵E是AB的中点,
∴AE=BE,
∵∠AEP=∠BEM,∠PAE=∠EBM,
∴△PAE≌△MBE(ASA),
∴AP=BM,
同理得:PD=CN,
∵AD=KG,BC=2AD,
∴MN=3AD,
∵PM⊥PN,
∴∠MPN=90°,
∵H是MN的中点,
∴PH=MN,
设BC=2AD=4k,AP=GQ=MB=a,则BG=k,MN=6k,PH=3k,
∵tan∠ABC==m,
∴PQ=AG=km,
∵PQ2=PH2﹣QH2,
即k2m2=9k2﹣(2k﹣2a)2,
∴m2=﹣++5=﹣(a﹣k)2+9,
又∵0<a<2k,
当a=0时,m2=5,
当a=k时,Q与H重合,不符合题意,
∴5<m2<9,
∴<m<3.
故答案为:<m<3.
18.解:①当△ABC为锐角三角形时,
过点A作AD⊥BC于点D,如图,
∵AB=3,∠B=45°,
∴AD=BD=AB sin45°=3,
∴CD==3,
∴BC=BD+CD=3+3;
②当△ABC为钝角三角形时,
过点A作AD⊥BC交BC延长线于点D,如图,
∵AB=3,∠B=45°,
∴AD=BD=AB sin45°=3,
∴CD==3,
∴BC=BD﹣CD=3﹣3;
综上,BC的长为3+3或3﹣3.
19.解:延长BD交AC于点E.
∵DC平分∠ACB,BD⊥CD于点D,
∴∠CDE=∠CDB=90°,∠DCE=∠DCB.
在△DCE和△DCB中,
,
∴△DCE≌△DCB(SAS).
∴BD=ED=1.
∵∠ABD=∠A,
∴AE=BE=2.
∵AC=7,
∴CE=AC﹣AE=5.
∴CD=
=
=2.
∴tan∠CBD===2.
故答案为:2.
20.解:设小正方形的边长为1,则AD=5,BC=4,
∵AD∥BC,
∴===,
由勾股定理得:BD==,DC==,AC==2,
则DE=BD=,CE=AC=,
过C作CF⊥BD于F,
∵△BCD的面积S=4×2=4,
∴△DCE的面积为×4=,
∴CF=,
∴××CF=,
∴CF=,
由勾股定理得:EF===,
∴tan∠CED===,
故答案为:.
21.解:如图所示,当∠C为钝角时,过点A作AD⊥BC,交BC的延长线于点D.
在Rt△ABD中,
∵AB=2,=,
∴AD=2.
∴BD==2.
在Rt△ACD中,
CD==1.
∴BC=BD﹣CD=1.
如图所示,当∠C为锐角时,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,
∵AB=2,=,
∴AD=2.
∴BD==2.
在Rt△ACD中,
CD==1.
∴BC=BD+CD=3.
故答案为:1或3.
22.解:如图,取格点T,连接AT,BT,设BT的中点为H,连接CH.
∵BC==5,CT==5,
∴CB=CT,
∵BH=HT,
∴∠HCA=∠HCB,CH⊥BT,
∵HT=,
∴sin===,
故答案为:.
23.解:过点A作AM⊥y轴于点M,作AN⊥BN交于点N,
∵直线y=﹣2与x轴平行,
∴∠ABN=α,
当sinα的值最大时,则tanα=值最大,
故BN最小,即BG最大时,tanα最大,
即当BG最大时,sinα的值最大,
设BG=m,
则AM=4,GC=n+2,CM=3﹣n,
∵∠ACM+∠MAC=90°,∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
∴tan∠CAM=tan∠BCG,
∴,即=,
∴m=﹣(n﹣3)(n+2)=﹣(n﹣)2+,
∵﹣<0,
∴当n=时,m取得最大值,
故n=,
故答案为:.
三.解答题
24.解:(1)sin75°=sin(30°+45°)
=sin30° cos45°+cos30° sin45°
=+
=;
(2)①过C′作C′E⊥l于E,
∵△ABC是等边三角形且边长为2,
∴C′E=,AE=2+2+1=5,
∴tan∠CAC′==;
②过A′作A′F⊥l于F,
∵△ABC是等边三角形且边长为2,
∴A′F=,AF=2+2+2+2+1=9,
∴tan∠CAA′==.
设∠CAC′=α,∠CAA′=β,
tan(α+β)===,
∴α+β=30°,
∴∠CAC′+CAA′=30°.
25.解:①能消去②中的AC、BC、CD.
将AC BC sin(α+β)=AC CD sinα+BC CD sinβ,两边同除以AC BC得:
sin(α+β)= sinα+ sinβ③,
又∵cosβ=、cosα=,
代入③可得:sin(α+β)=sinα cosβ+cosα sinβ.
②由sin(α+β)=sinα cosβ+cosα sinβ得:sin75°=sin(30°+45°)=sin30° cos45°+cos30° sin45°
=×+×
=.
26.解:(1)由题意得:sin120°=sin(180°﹣120°)=sin60°=,cos150°=cos(180°﹣30°)=﹣cos30°=﹣;
(2)∵一个钝角三角形的三个内角比是1:1:4,
∴三个内角分别为30°,30°,120°,
①当∠A=30°,∠B=120°时,方程的两根为,﹣,
把代入方程得:1﹣m﹣1=0,解得:m=0,
经检验﹣是4x2﹣1=0的根,故m=0;
②当∠A=120°,∠B=30°时,方程的两根为,,不符合题意;
③∠A=30°,∠B=30°时,方程两根为,,
把代入得:1﹣m﹣1=0,解得:m=0,
经检验不是方程4x2﹣1=0的根,不符合题意,
则m=0,∠A=30°,∠B=120°.
27.解:∵sinB=,cosB=,
∴AD=AB sinB=c sinB,BD=AB cosB=c cosB,
CD=BC﹣BD=a﹣c cosB,
则出b2=AD2+DC2=(c sinB)2+(a﹣c cosB)2
=c2sin2B+a2+c2cos2B+2ac cosB
=c2(sin2B+cos2B)+a2﹣2ac cosB
=a2+c2﹣2ac cosB.
如图3所示,延长BC,AD交于E,
∵∠B=90°,∠BAD=60°,AB=4,
∴AE=2AB=8,∠E=30°,
∵AD=5,
∴DE=3,
∵∠ADC=∠CDE=90°,
∴CE=2,
∴AC2=CE2+AE2﹣2CE AEcos30°=12+64﹣2××8×=28,
∴AC=2.
故答案是:c sinB,c cosB;a2+c2﹣2ac cosB.
28.解:(1)如图,过点P作PH⊥AB于H.
∵∠BPC=90°,PB=,BC=1,
∴cos∠CBP==,
∴∠CBP=60°,
∵∠ABC=90°,
∴∠PBH=90°﹣60°=30°,
∴PH=PB=,BH=PH=,
∵AB=,
∴AH=AB﹣BH=,
∴AP==.
(2)如图,过点A作AT⊥BP交BP的延长线于T.
∵tan∠TBA==,AB=,
∴AT=,BT=,
∵∠BCP+∠CBP=90°,∠CBP+∠ABP=90°,
∴∠BCP=∠ABP,
∴tan∠CBP=,
∵BC=1,
∴PB=,
∴PT=BT﹣PB=,
∴tan∠APT==,
∴∠APT=60°,
∴∠APB=120°.
29.解:(1)如图1.
∵BC2=32+52=34,AB2=42+12=17,AC2=42+12=17,
∴BC2=AB2+AC2=2AB2,
∴△ABC是等腰直角三角形,且∠BAC=90°,
∴α+β=∠ABC=45°.
故答案为45;
(2)如图2,连接MN.
∵OM2=32+12=10,ON2=22+12=5,MN2=22+12=5,
∴OM2=ON2+MN2=2ON2,
∴△OMN是等腰直角三角形,且∠ONM=90°,
∴α﹣β=∠MON=45°
