中位线定理[下学期]
图片预览


文档简介
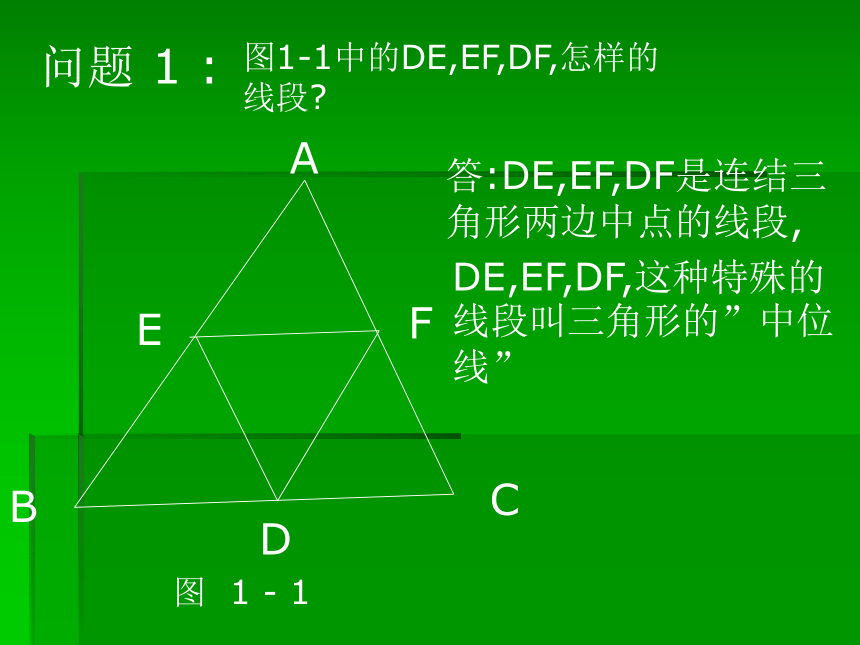
课件8张PPT。 角 形 中 位 线荣成二十一中学问题 1 :图1-1中的DE,EF,DF,怎样的线段?A 图 1 - 1答:DE,EF,DF是连结三角形两边中点的线段,DE,EF,DF,这种特殊的线段叫三角形的”中位线” 问题2:你能给”三角形的中位线”下一个定义?
一个三角形有几条中位线?三角形的中
位线与中线的区别?答:中位线则是两边中点的连线;一个三角形的三边有三个中点,因此可以连出三条中位线.
三角形的中线与三解形的中位线的区别:中线的两个端点是三角形的的一边中点和这边所对的顶点;中位线则是两边中点的连线;中线把三角形的面积微积等分,而中位线不具有这个性质,但它会有其它一些性质.三角形的中位线:连结三角形的两边中点
的线段.
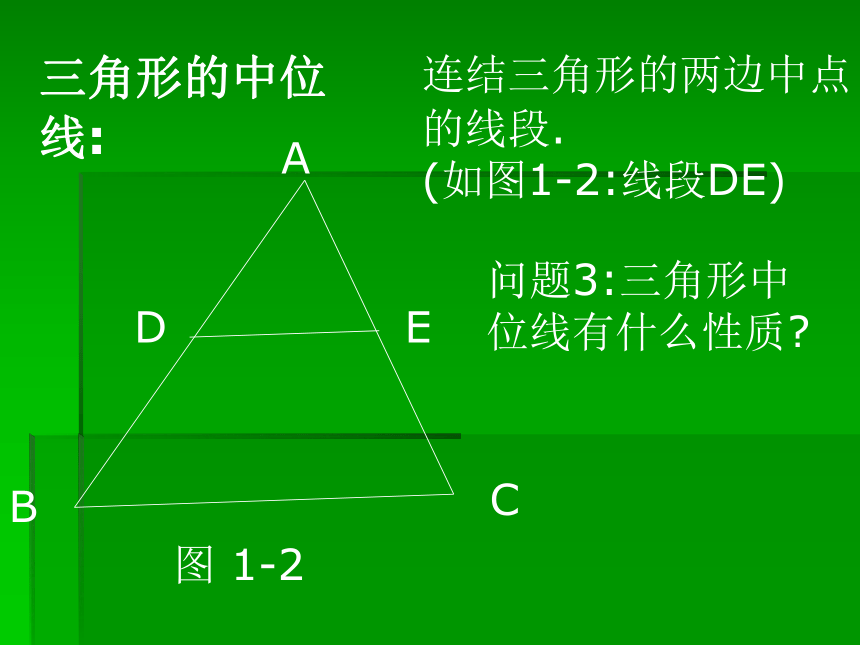
(如图1-2:线段DE)BCEDA问题3:三角形中
位线有什么性质?图 1-2BCEFDA(E’)1,如图,DE是⊿ABC
一条中位线,如果过
D作DE∥BC,交AC
于E’,那么根椐平行
线等分线段定推论2,
E’是AC的中点,可见
DE与DE’重合.因此
DE∥BC.三角形中位线定理三角形的中位线平行于第三边
并且等于它的一半A如图:DE,DF ,EF为三角形ABC的中位线
∴EF∥BC EF= BC
DF∥AB DF= AB
DE∥AC DE= AC 例题:已知:如图1-3,在四边形ABCD中,E,F,
是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.证明: 连结AC.∵AH=HD,CG=GD,
∴HG∥AC,HG= AC
(三角形中位线定理).
同理 EF∥AC,EF= AC.
∴HG∥EF HG=EF.
所以四边形EFGH是平行四边形 练习:
1,已知三角形的各边分6cm,8cm和10cm,求连结各边中点成三角形的周长. 2,求证:三角形的一条中位线与第三边上
的中线互相平分
一个三角形有几条中位线?三角形的中
位线与中线的区别?答:中位线则是两边中点的连线;一个三角形的三边有三个中点,因此可以连出三条中位线.
三角形的中线与三解形的中位线的区别:中线的两个端点是三角形的的一边中点和这边所对的顶点;中位线则是两边中点的连线;中线把三角形的面积微积等分,而中位线不具有这个性质,但它会有其它一些性质.三角形的中位线:连结三角形的两边中点
的线段.
(如图1-2:线段DE)BCEDA问题3:三角形中
位线有什么性质?图 1-2BCEFDA(E’)1,如图,DE是⊿ABC
一条中位线,如果过
D作DE∥BC,交AC
于E’,那么根椐平行
线等分线段定推论2,
E’是AC的中点,可见
DE与DE’重合.因此
DE∥BC.三角形中位线定理三角形的中位线平行于第三边
并且等于它的一半A如图:DE,DF ,EF为三角形ABC的中位线
∴EF∥BC EF= BC
DF∥AB DF= AB
DE∥AC DE= AC 例题:已知:如图1-3,在四边形ABCD中,E,F,
是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.证明: 连结AC.∵AH=HD,CG=GD,
∴HG∥AC,HG= AC
(三角形中位线定理).
同理 EF∥AC,EF= AC.
∴HG∥EF HG=EF.
所以四边形EFGH是平行四边形 练习:
1,已知三角形的各边分6cm,8cm和10cm,求连结各边中点成三角形的周长. 2,求证:三角形的一条中位线与第三边上
的中线互相平分
