三角函数复习[下学期]
图片预览





文档简介
课件14张PPT。热烈欢迎各位领导、教师莅临指导三角函数复习(一)2007中考考试目标三角函数
(1)认识三角函数,知道 30°、 45°、 60°角的三角函数值
(2) 由已知特殊三角函数值求它对应的锐角
(3)运用三角函数解决与直角三角形有关的简单的实际问题
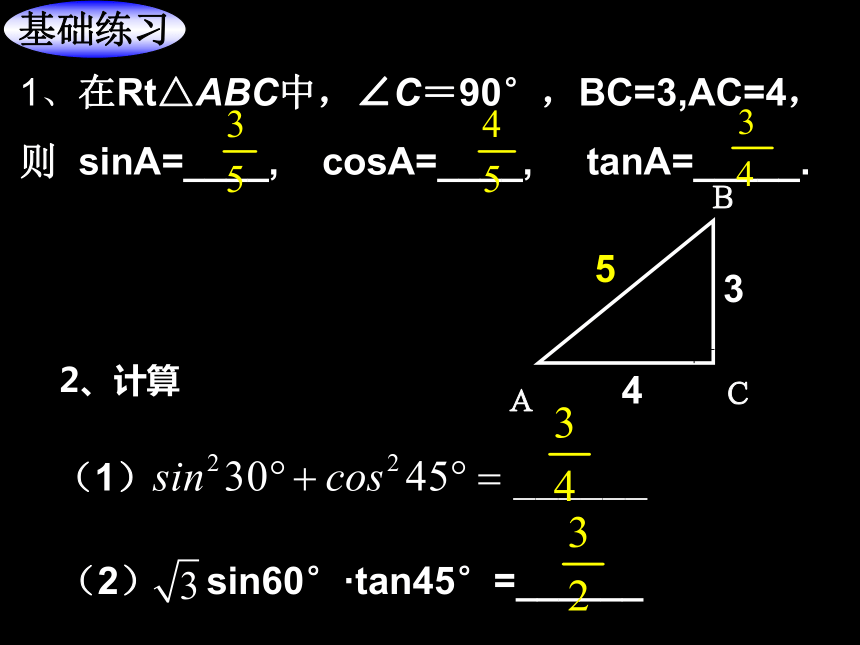
基础练习1、在Rt△ABC中,∠C=90°,BC=3,AC=4,
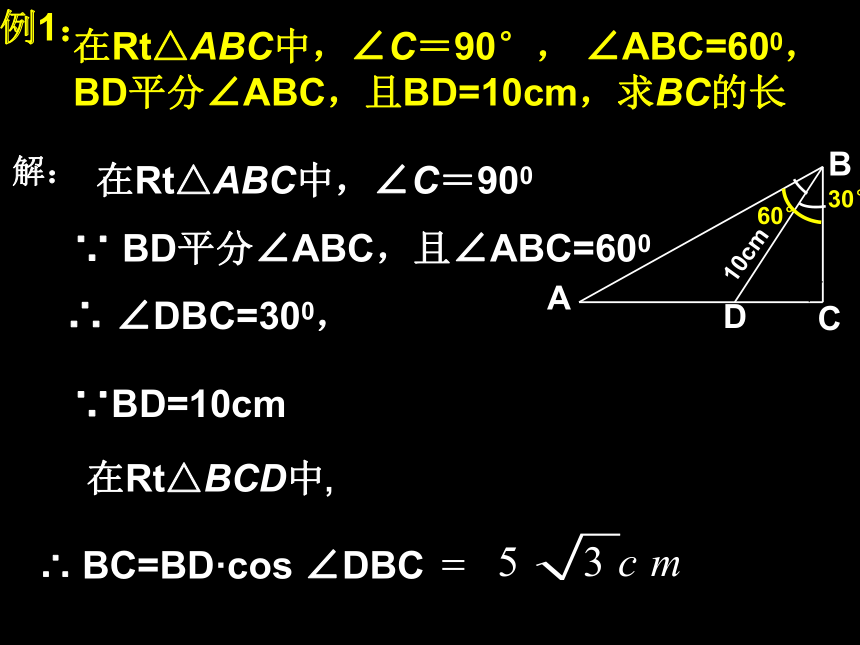
则 sinA=____, cosA=____, tanA=_____.52、计算(1)例1:在Rt△ABC中,∠C=90°, ∠ABC=600,BD平分∠ABC,且BD=10cm,求BC的长∴ ∠DBC=300,∵BD=10cm∴ BC=BD·cos ∠DBC在Rt△BCD中,ACBD60°10cm30°例2 如图,山顶上有一旗杆BC,在地面上一点A处测得杆顶B的仰角为 600,杆底C的仰角为450,已知旗杆高BC=20米,求山高CD。4560°ABCD20x解:在Rt△ACD中,设CD=x ∵ ∠CAD= 45°∴ AD=CD=x在Rt△ABD中, ∠BAD= 60°∴ tan ∠BAD=所以 山高CD为 米x即:∴B船在A处测得北偏东450方向有一座灯塔B,船向正东方向以每小时20海里的速度航行了1.5小时,到达C处时,测得灯塔在北偏东300方向上,求此时船与灯塔相距多少海里?设CD=x 巩固练习:BD30?小明同学想测量我们学校的旗杆,聪明的你有什么方法可以帮他轻松地测出旗杆的高度?请你设计一个方案知识运用皮尺,镜子 (竹竿,测角仪) 小结本章知识结构:锐角三角函数sinA
cosA
tanA解直角三角形实际问题的解决30° 45° 60°的三角函数值2、在Rt△ABC中,∠C=90°,BC= AC,
则sinA=_____ 1、在Rt△ABC中,∠C=90°,BC= ,AC=3 ,则AB_____. ∠A=______, ∠B=_______.ACB3、在Rt△ABC中,∠C=90°,tanA= ,
则cosA=______ . 30°60°达标训练5、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC= ,AB= , 设∠ BCD=α,那么cos α的值等于( )DA、 B、 C、 D、D4、小明沿着坡角为30°的坡面向下走了2米,那么他下降( )
A.1米 B. 米 C. D.A7.一根长4m的竹竿斜靠在墙上.
如果竹竿上端顺墙下滑到高度 m处停止,那么此时竹竿与地面所成锐角为______.
6、如果sinA·cos60°= , 则A=_____。8、如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC提示:作AD⊥BC于D60°45°AC=8
如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为600,爬到楼顶D处测得塔顶的仰角为300,求塔高BC及大楼与塔之间的距离AC能力提升3030°分析:∵ ∠CAB= 60°
∠BDE= 30°∴ ∠ABD= 30°∴ BD= AD=30∴ DE= BD·cos 30° =BE= BD=15同学们再见
(1)认识三角函数,知道 30°、 45°、 60°角的三角函数值
(2) 由已知特殊三角函数值求它对应的锐角
(3)运用三角函数解决与直角三角形有关的简单的实际问题
基础练习1、在Rt△ABC中,∠C=90°,BC=3,AC=4,
则 sinA=____, cosA=____, tanA=_____.52、计算(1)例1:在Rt△ABC中,∠C=90°, ∠ABC=600,BD平分∠ABC,且BD=10cm,求BC的长∴ ∠DBC=300,∵BD=10cm∴ BC=BD·cos ∠DBC在Rt△BCD中,ACBD60°10cm30°例2 如图,山顶上有一旗杆BC,在地面上一点A处测得杆顶B的仰角为 600,杆底C的仰角为450,已知旗杆高BC=20米,求山高CD。4560°ABCD20x解:在Rt△ACD中,设CD=x ∵ ∠CAD= 45°∴ AD=CD=x在Rt△ABD中, ∠BAD= 60°∴ tan ∠BAD=所以 山高CD为 米x即:∴B船在A处测得北偏东450方向有一座灯塔B,船向正东方向以每小时20海里的速度航行了1.5小时,到达C处时,测得灯塔在北偏东300方向上,求此时船与灯塔相距多少海里?设CD=x 巩固练习:BD30?小明同学想测量我们学校的旗杆,聪明的你有什么方法可以帮他轻松地测出旗杆的高度?请你设计一个方案知识运用皮尺,镜子 (竹竿,测角仪) 小结本章知识结构:锐角三角函数sinA
cosA
tanA解直角三角形实际问题的解决30° 45° 60°的三角函数值2、在Rt△ABC中,∠C=90°,BC= AC,
则sinA=_____ 1、在Rt△ABC中,∠C=90°,BC= ,AC=3 ,则AB_____. ∠A=______, ∠B=_______.ACB3、在Rt△ABC中,∠C=90°,tanA= ,
则cosA=______ . 30°60°达标训练5、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC= ,AB= , 设∠ BCD=α,那么cos α的值等于( )DA、 B、 C、 D、D4、小明沿着坡角为30°的坡面向下走了2米,那么他下降( )
A.1米 B. 米 C. D.A7.一根长4m的竹竿斜靠在墙上.
如果竹竿上端顺墙下滑到高度 m处停止,那么此时竹竿与地面所成锐角为______.
6、如果sinA·cos60°= , 则A=_____。8、如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC提示:作AD⊥BC于D60°45°AC=8
如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为600,爬到楼顶D处测得塔顶的仰角为300,求塔高BC及大楼与塔之间的距离AC能力提升3030°分析:∵ ∠CAB= 60°
∠BDE= 30°∴ ∠ABD= 30°∴ BD= AD=30∴ DE= BD·cos 30° =BE= BD=15同学们再见
