2022-2023学年山东省泰安市肥城市八年级(下)期末数学试卷(五四学制)(含解析)
文档属性
| 名称 | 2022-2023学年山东省泰安市肥城市八年级(下)期末数学试卷(五四学制)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 16:01:30 | ||
图片预览




文档简介
2022-2023学年山东省泰安市肥城市八年级(下)期末数学试卷(五四学制)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列根式是最简二次根式的是( )
A. B. C. D.
2. 用配方法解方程,可变形为( )
A. B. C. D.
3. 下列计算,正确的是( )
A. B. C. D.
4. 如图,直线,直线交、、于点、、,直线交、、于点、、,已知,若,则的长是( )
A.
B.
C.
D.
5. 如图 ,为中点,延长至,使::,连接交于点,则:( )
A. : B. : C. : D. :
6. 如图,在中,点是边上的点与,两点不重合,过点作,,分别交,于,两点,下列说法正确的是( )
A. 若,则四边形是矩形
B. 若垂直平分,则四边形是矩形
C. 若,则四边形是菱形
D. 若平分,则四边形是菱形
7. 已知,那么化简代数式的结果是( )
A. B. C. D.
8. 电影长津湖上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达亿元,将增长率记作,则方程可以列为( )
A. B.
C. D.
9. 如图,在正方形中,,分别为边,的中点,连接,,点,分别为,的中点,连接,则的长为( )
A.
B.
C.
D.
10. 如图,两张等宽的纸条交叉重叠在一起,重叠部分四边形的对角线、的长度是关于的一元二次方程的两个实数根,则四边形的面积可以表示为( )
A.
B.
C.
D.
11. 如图,矩形与矩形是位似图形,点是位似中心.若点的坐标为,点的横坐标为,则点的坐标为( )
A.
B.
C.
D.
12. 如图,菱形的边长为,且,是的中点,为上一点且的周长最小,则的周长的最小值为( )
A. B. C. D.
二、填空题(本大题共6小题,共18.0分)
13. 若关于的方程有实数根,则实数的取值范围是______ .
14. 如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是 .
15. 已知,,则______.
16. 如图,在中,,,分别是,的中点,动点在射线上,交于点,的平分线交于点,当时,的值为______ .
17. 如图,菱形的对角线交于点,,,,垂足为,则的长度为______ .
18. 人们把这个数叫做黄金分割数,著名数学家华罗庚优选法中的法就应用了黄金分割数设,,得,记,,,,则 .
三、解答题(本大题共8小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
19. 本小题分
计算:
;
.
20. 本小题分
按要求解下列方程:
配方法;
自己喜欢的方法.
21. 本小题分
小军在学习相似三角形时,遇到这样一个问题:
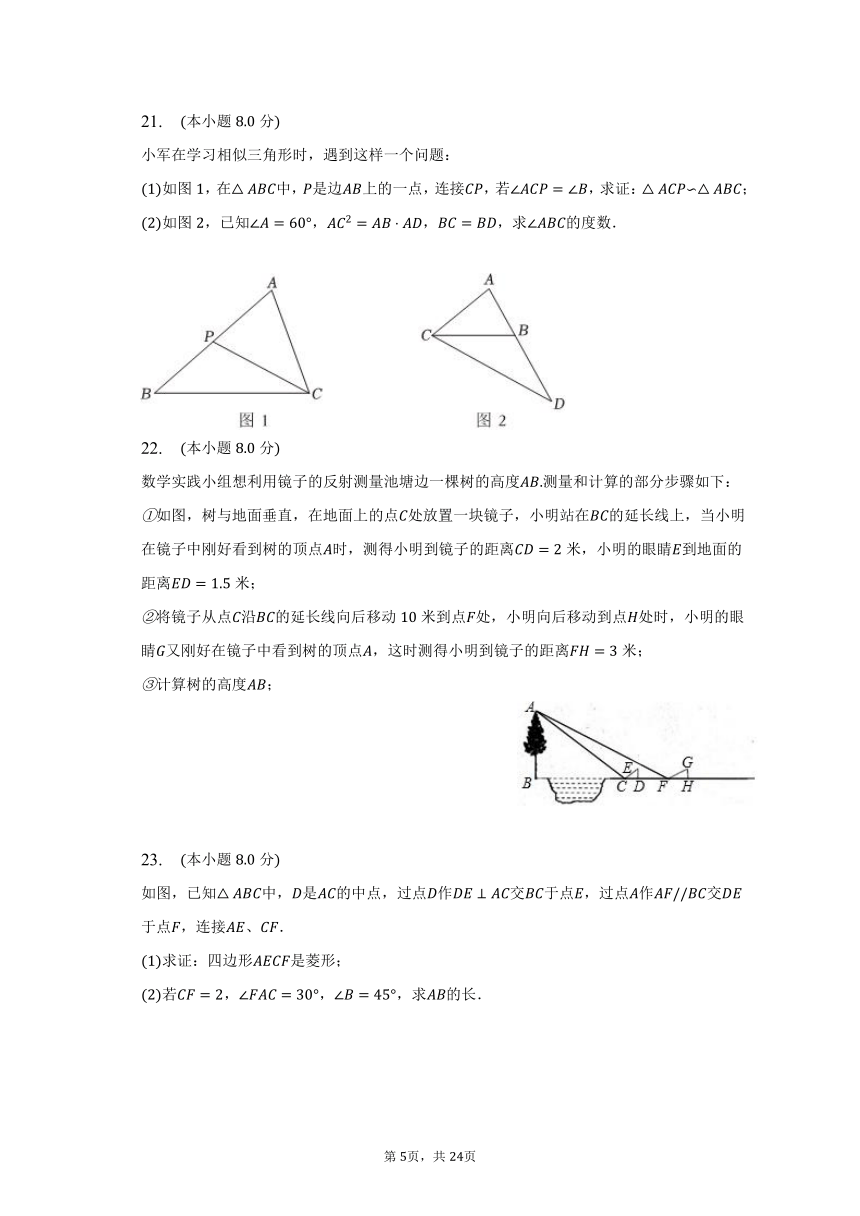
如图,在中,是边上的一点,连接,若,求证:∽;
如图,已知,,,求的度数.
22. 本小题分
数学实践小组想利用镜子的反射测量池塘边一棵树的高度测量和计算的部分步骤如下:
如图,树与地面垂直,在地面上的点处放置一块镜子,小明站在的延长线上,当小明在镜子中刚好看到树的顶点时,测得小明到镜子的距离米,小明的眼睛到地面的距离米;
将镜子从点沿的延长线向后移动米到点处,小明向后移动到点处时,小明的眼睛又刚好在镜子中看到树的顶点,这时测得小明到镜子的距离米;
计算树的高度;
23. 本小题分
如图,已知中,是的中点,过点作交于点,过点作交于点,连接、.
求证:四边形是菱形;
若,,,求的长.
24. 本小题分
年是我国脱贫胜利年,我国在扶贫方面取得了巨大的成就,技术扶贫也使得某县的一个电子器件厂扭亏为盈.该电子器件厂生产一种电脑显卡,年该类电脑显卡的成本是元个,年与年连续两年在技术扶贫的帮助下改进技术,降低成本,年该电脑显卡的成本降低到元个.
若这两年此类电脑显卡成本下降的百分率相同,求平均每年下降的百分率;
年某商场以高于成本价的价格购进若干个此类电脑显卡,以元个销售时,平均每天可销售个,为了减少库存,商场决定降价销售.经调查发现,单价每降低元,每天可多售出个,如果每天盈利元,单价应降低多少元?
25. 本小题分
如图,在正方形中,点为对角线、交点,平分交于点,交于点.
求证:∽;
判断的形状并说明理由;
若,求的长.
26. 本小题分
附加题本题仅供有兴趣的同学选择使用
如图,点是内一点,且,,,,求的值.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了最简二次根式,最简二次根式是被开方数不含分母,被开方数不含开的尽的因数或因式.
根据最简二次根式是被开方数不含分母,被开方数不含开的尽的因数或因式,可得答案.
【解答】
解:、该二次根式的被开方数中含有分母,不是最简二次根式,故本选项错误;
B、该二次根式的被开方数中含有小数,不是最简二次根式,故本选项错误;
C、该二次根式符合最简二次根式的定义,故本选项正确;
D、,该二次根式的被开方数中含开的尽的因数,不是最简二次根式,故本选项错误,
故选:.
2.【答案】
【解析】解:,
,
,
,所以选项和选项不符合题意,选项符合题意;
可化为,所以选项不符合题意.
故选:.
先把常数项移到方程右边,再把二次项系数化为,然后方程两边加上,最后把方程左边写成完全平方的形式即可,从而可对各选项进行判断.
本题考查了解一元二次方程配方法:熟练掌握用配方法解一元二次方程的一般步骤是解决问题的关键.
3.【答案】
【解析】解:、、不是同类二次根式,不能合并,故选项错误;
C、,故选项正确.
故选C.
A、、、根据合并同类二次根式的法则即可判定;
D、利用根式的运算法则计算即可判定.
此题主要考查二次根式的运算,应熟练掌握各种运算法则,且准确计算.
4.【答案】
【解析】解:直线,
.
,,
,
,
.
故选:.
由直线可得出,结合,可得出的值,进而可得出,再将其代入中即可求出结论.
本题考查了平行线分线段成比例,牢记“三条平行线截两条直线,所得的对应线段成比例”是解题的关键.
5.【答案】
【解析】
【分析】
本题主要考查了相似三角形的判定和性质,平行四边形的性质,中点的定义表示出是解题的关键.
先设出,进而得出,再用平行四边形的性质得出,进而求出,最后用相似三角形的性质即可得出结论.
【解答】
解:设,
::,
,
四边形是平行四边形,
,,
点是的中点,
,
,
∽,
,
故选:.
6.【答案】
【解析】
【解答】
解:若,则四边形是平行四边形,不一定是矩形;选项A错误;
若垂直平分,则四边形是菱形,不一定是矩形;选项B错误;
若,则四边形是平行四边形,不一定是菱形;选项C错误;
若平分,则四边形是菱形;正确;
故选:.
【分析】
由矩形的判定和菱形的判定即可得出结论.
本题考查了矩形的判定、菱形的判定;熟记菱形和矩形的判定方法是解决问题的关键.
7.【答案】
【解析】解:,
,,
,
故选:.
先把被开方数分解因式,再化简求值.
本题考查二次根式的性质与化简,掌握完全平方公式的特点是解题的关键.
8.【答案】
【解析】解:设平均每天票房的增长率为,
根据题意得:.
故选:.
第一天为,根据增长率为,得出第二天为,第三天为,根据三天累计为,即可得出关于的一元二次方程.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
9.【答案】
【解析】解:连接,延长交于,连接,
四边形是正方形,
,,,
,,
为的中点,
,
在和中,
,
≌,
,,
,
点为的中点,
,
为的中点,
,
,
,
故选:.
连接,延长交于,连接,由正方形推出,,,证得≌,得到,,根据三角形中位线定理得到,由勾股定理求出即可得到.
本题主要考查了正方形的性质,全等三角形的性质和判定,勾股定理,三角形的中位线定理,正确作出辅助线且证出是解决问题的关键.
10.【答案】
【解析】解:过点作于,过点作于,如图,
由题意得,,,
四边形为平行四边形,
,
,
四边形为菱形,
四边形的面积,
、的长度是关于的一元二次方程的两个实数根,
,
四边形的面积
故选:.
过点作于,过点作于,如图,利用纸条等宽得到,,,则可判断四边形为平行四边形,接着利用面积法得到,于是可判断四边形为菱形,利用菱形的面积公式得到四边形的面积,然后根据根与系数的关系进行判断.
本题考查了根与系数的关系:若,是一元二次方程的两根时,,也考查了菱形的判定与性质.
11.【答案】
【解析】解:四边形为矩形,点的坐标为,
,,
矩形与矩形是位似图形,
,,
∽,∽,
,,
,,
解得:,,
点的坐标为,
故选:.
根据位似图形的概念得到,,进而证明∽,∽,根据相似三角形的性质求出,得到答案.
本题考查的是位似图形的概念、相似三角形的性质,根据位似图形的概念得出,是解题的关键.
12.【答案】
【解析】解:连接交于点,连接,,
四边形是菱形,
对角线所在直线是其一条对称轴,点,点关于直线对称,
,
是的中点,
,
的周长,
要求的周长的最小值可先求出的最小值即可,
而的最小值就是的长,
过点作,交的延长线于点,
四边形是菱形,
,
,
在中,
,,
在中,
,,
,
的周长的最小值为,
故选:.
首先确定出的周长的最小值就是的最小值,然后利用将军饮马问题的模型构造出的周长的最小值,再利用勾股定理求出,进而解决问题.
本题考查轴对称最短路线问题,菱形的性质,勾股定理,特殊值的三角函数,掌握相关图形的性质和构造出最短路线是解题的关键.
13.【答案】
【解析】解:关于的方程有实数根,
当时,,
,
且,
当时,
此时方程为,满足题意,
故答案为:.
根据一元二次方程的根的判别式即可求出答案.
本题考查一元二次方程,解题的关键是正确理解根的判别式,本题属于基础题型.
14.【答案】或
【解析】
【分析】
把点的横纵坐标分别乘以或即可得到点的坐标.
本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形中对应点的坐标的比等于或.
【解答】
解:位似中心为原点,相似比为,
点的对应点的坐标为或,即或.
故答案为或.
15.【答案】
【解析】解:,,
;
故答案为:.
先把要求的式子变形为,再代入计算即可.
此题考查了二次根式的化简求值,用到的知识点是平方差公式、因式分解,关键是通过因式分解把要求的式子进行变形.
16.【答案】
【解析】解:如图,延长交射线于,
、分别是、的中点,
,
,
是的平分线,
,
,
,
,
,
,
由得,∽,
,
,
即.
故答案为:.
延长交射线于,根据三角形的中位线平行于第三边可得,根据两直线平行,内错角相等可得,再根据角平分线的定义可得,从而得到,根据等角对等边可得,求出,再根据,求出,然后根据和相似,利用相似三角形对应边成比例列式求解即可.
本题考查了三角形中位线定理、相似三角形的判定与性质,角平分线的定义,平行线的性质,延长构造出相似三角形,求出并得到相似三角形是解题的关键,也是本题的难点.
17.【答案】
【解析】解:四边形是菱形,
,,,
在中,,
,
,
根据菱形的面积公式可得,利用勾股定理求出即可.
本题考查菱形的性质、勾股定理等知识,解题的关键是利用菱形的两种面积公式,构建方程解决问题.
18.【答案】
【解析】
【分析】
利用分式的加减法则分别求得,,,即可求解.
本题考查了分式的加减法,找出其中的规律是解本题的关键.
【解答】
解:,
,
,
,
,
故答案为.
19.【答案】解:原式
;
原式
.
【解析】先根据二次根式的乘法法则和零次幂的运算法则进行计算,再合并同类二次根式即可;
先根据平方差公式、二次根式的性质、完全平方公式进行计算,再合并同类二次根式即可.
本题主要考查二次根式的混合运算、零指数幂,熟练掌握二次根式的运算法则、平方差公式、完全平方公式是解题关键.
20.【答案】解:,
,
,
,
,
,
或,
,;
,
,
,
,
,.
【解析】利用解一元二次方程配方法,进行计算即可解答;
利用解一元二次方程因式分解法,进行计算即可解答.
本题考查了解一元二次方程配方法,因式分解法,熟练掌握解一元二次方程的方法是解题的关键.
21.【答案】证明:,,
∽;
解:,
::,
又,
∽,
,
,
,
,
,,
,
,
,
.
【解析】根据,即可得出结论;
先由得::,再根据可判定和相似,进而得,然后由得,据此可得出,然后利用三角形的内角和定理可求出,进而可求出的度数.
此题主要考查了相似三角形的判定和性质,等腰三角形的性质,三角形的内角和定理,解答此题的关键是理解两个角对应相等的两个三角形相似;两边对应成比例,且夹角相等的两个三角形相似;相似三角形的对应边成比例、对应角相等.
22.【答案】解:设米,米.
,
∽
,
,
,,
∽,
,
,
,
解得:,
把代入中,得,
树的高度为米.
【解析】根据题意得出∽,利用相似三角形的性质得出,的长进而得出答案.
此题主要考查了相似三角形的应用,正确应用相似三角形的判定与性质是解题关键.
23.【答案】解:证明:如图,
在中,点是的中点,
,
,
,,
≌,
,
四边形是平行四边形,
又,点是的中点,即垂直平分,
,
平行四边形是菱形.
如图,过点作于点,
由知四边形是菱形,又,,
,,,
,
,
,
,
,,
,
,
,
.
【解析】由题意可得≌,则,根据“一组对边平行且相等的四边形是平行四边形”可得四边形是平行四边形;又垂直平分,根据垂直平分线的性质可得,根据“有一组临边相等的平行四边形是菱形”可得结论;
过点作于点,根据题意可得,,则,.
本题主要考查菱形的性质与判定,含角的直角三角形的三边关系,等腰直角三角形的性质与判定等内容,根据,等特殊角作出正确的垂线是解题关键.
24.【答案】解:设平均每年下降的百分率为,
依题意,得.
解得,不合题意,舍去.
答:平均每年下降的百分率为.
设单价应降低元,则每个的销售利润为元,每天可售出个,
依题意得:.
整理,得.
解得,.
为了减少库存,
,
答:单价应降低元.
【解析】设平均每年下降的百分率为,利用年该类电脑显卡的出厂价年该类电脑显卡的出厂价下降率,即可得出关于的一元二次方程,解之取其符合题意的值即可得出结论;
设单价应降低元,则每个的销售利润为元,每天可售出个,利用每天销售该电脑显卡获得的利润每个的销售利润日销售量,即可得出关于的一元二次方程,解之即可得出的值即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
25.【答案】证明:四边形是正方形,
,,
,
平分,
,
∽.
解:结论:是等腰三角形.
理由:四边形是正方形,
,,
平分,
,
,,
,
是等腰三角形;
解:四边形是正方形,
,,
是等腰直角三角形;
,
∽,
,
,
,
.
【解析】证明两个角对应相等即可.
通过计算证明,推出.
证明,利用相似三角形的性质解决问题即可.
本题属于相似形综合题,考查了正方形的性质,等腰直角三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题.
26.【答案】解:如图,过点作的垂线,过点作的垂线,两垂线交于点,连接,
,
,
,
,
又,
∽,
,
又,
,
即,
∽,
,
,
,
在中,,
.
【解析】过点作的垂线,过点作的垂线,两垂线交于点,连接,证明∽,由相似三角形的性质得出,证明∽,得出,求出,由勾股定理求出,最后由直角三角形的性质可求出的长.
此题主要考查相似三角形的判定与性质,作出正确的辅助线是解题的关键.
第1页,共1页
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列根式是最简二次根式的是( )
A. B. C. D.
2. 用配方法解方程,可变形为( )
A. B. C. D.
3. 下列计算,正确的是( )
A. B. C. D.
4. 如图,直线,直线交、、于点、、,直线交、、于点、、,已知,若,则的长是( )
A.
B.
C.
D.
5. 如图 ,为中点,延长至,使::,连接交于点,则:( )
A. : B. : C. : D. :
6. 如图,在中,点是边上的点与,两点不重合,过点作,,分别交,于,两点,下列说法正确的是( )
A. 若,则四边形是矩形
B. 若垂直平分,则四边形是矩形
C. 若,则四边形是菱形
D. 若平分,则四边形是菱形
7. 已知,那么化简代数式的结果是( )
A. B. C. D.
8. 电影长津湖上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达亿元,将增长率记作,则方程可以列为( )
A. B.
C. D.
9. 如图,在正方形中,,分别为边,的中点,连接,,点,分别为,的中点,连接,则的长为( )
A.
B.
C.
D.
10. 如图,两张等宽的纸条交叉重叠在一起,重叠部分四边形的对角线、的长度是关于的一元二次方程的两个实数根,则四边形的面积可以表示为( )
A.
B.
C.
D.
11. 如图,矩形与矩形是位似图形,点是位似中心.若点的坐标为,点的横坐标为,则点的坐标为( )
A.
B.
C.
D.
12. 如图,菱形的边长为,且,是的中点,为上一点且的周长最小,则的周长的最小值为( )
A. B. C. D.
二、填空题(本大题共6小题,共18.0分)
13. 若关于的方程有实数根,则实数的取值范围是______ .
14. 如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是 .
15. 已知,,则______.
16. 如图,在中,,,分别是,的中点,动点在射线上,交于点,的平分线交于点,当时,的值为______ .
17. 如图,菱形的对角线交于点,,,,垂足为,则的长度为______ .
18. 人们把这个数叫做黄金分割数,著名数学家华罗庚优选法中的法就应用了黄金分割数设,,得,记,,,,则 .
三、解答题(本大题共8小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
19. 本小题分
计算:
;
.
20. 本小题分
按要求解下列方程:
配方法;
自己喜欢的方法.
21. 本小题分
小军在学习相似三角形时,遇到这样一个问题:
如图,在中,是边上的一点,连接,若,求证:∽;
如图,已知,,,求的度数.
22. 本小题分
数学实践小组想利用镜子的反射测量池塘边一棵树的高度测量和计算的部分步骤如下:
如图,树与地面垂直,在地面上的点处放置一块镜子,小明站在的延长线上,当小明在镜子中刚好看到树的顶点时,测得小明到镜子的距离米,小明的眼睛到地面的距离米;
将镜子从点沿的延长线向后移动米到点处,小明向后移动到点处时,小明的眼睛又刚好在镜子中看到树的顶点,这时测得小明到镜子的距离米;
计算树的高度;
23. 本小题分
如图,已知中,是的中点,过点作交于点,过点作交于点,连接、.
求证:四边形是菱形;
若,,,求的长.
24. 本小题分
年是我国脱贫胜利年,我国在扶贫方面取得了巨大的成就,技术扶贫也使得某县的一个电子器件厂扭亏为盈.该电子器件厂生产一种电脑显卡,年该类电脑显卡的成本是元个,年与年连续两年在技术扶贫的帮助下改进技术,降低成本,年该电脑显卡的成本降低到元个.
若这两年此类电脑显卡成本下降的百分率相同,求平均每年下降的百分率;
年某商场以高于成本价的价格购进若干个此类电脑显卡,以元个销售时,平均每天可销售个,为了减少库存,商场决定降价销售.经调查发现,单价每降低元,每天可多售出个,如果每天盈利元,单价应降低多少元?
25. 本小题分
如图,在正方形中,点为对角线、交点,平分交于点,交于点.
求证:∽;
判断的形状并说明理由;
若,求的长.
26. 本小题分
附加题本题仅供有兴趣的同学选择使用
如图,点是内一点,且,,,,求的值.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了最简二次根式,最简二次根式是被开方数不含分母,被开方数不含开的尽的因数或因式.
根据最简二次根式是被开方数不含分母,被开方数不含开的尽的因数或因式,可得答案.
【解答】
解:、该二次根式的被开方数中含有分母,不是最简二次根式,故本选项错误;
B、该二次根式的被开方数中含有小数,不是最简二次根式,故本选项错误;
C、该二次根式符合最简二次根式的定义,故本选项正确;
D、,该二次根式的被开方数中含开的尽的因数,不是最简二次根式,故本选项错误,
故选:.
2.【答案】
【解析】解:,
,
,
,所以选项和选项不符合题意,选项符合题意;
可化为,所以选项不符合题意.
故选:.
先把常数项移到方程右边,再把二次项系数化为,然后方程两边加上,最后把方程左边写成完全平方的形式即可,从而可对各选项进行判断.
本题考查了解一元二次方程配方法:熟练掌握用配方法解一元二次方程的一般步骤是解决问题的关键.
3.【答案】
【解析】解:、、不是同类二次根式,不能合并,故选项错误;
C、,故选项正确.
故选C.
A、、、根据合并同类二次根式的法则即可判定;
D、利用根式的运算法则计算即可判定.
此题主要考查二次根式的运算,应熟练掌握各种运算法则,且准确计算.
4.【答案】
【解析】解:直线,
.
,,
,
,
.
故选:.
由直线可得出,结合,可得出的值,进而可得出,再将其代入中即可求出结论.
本题考查了平行线分线段成比例,牢记“三条平行线截两条直线,所得的对应线段成比例”是解题的关键.
5.【答案】
【解析】
【分析】
本题主要考查了相似三角形的判定和性质,平行四边形的性质,中点的定义表示出是解题的关键.
先设出,进而得出,再用平行四边形的性质得出,进而求出,最后用相似三角形的性质即可得出结论.
【解答】
解:设,
::,
,
四边形是平行四边形,
,,
点是的中点,
,
,
∽,
,
故选:.
6.【答案】
【解析】
【解答】
解:若,则四边形是平行四边形,不一定是矩形;选项A错误;
若垂直平分,则四边形是菱形,不一定是矩形;选项B错误;
若,则四边形是平行四边形,不一定是菱形;选项C错误;
若平分,则四边形是菱形;正确;
故选:.
【分析】
由矩形的判定和菱形的判定即可得出结论.
本题考查了矩形的判定、菱形的判定;熟记菱形和矩形的判定方法是解决问题的关键.
7.【答案】
【解析】解:,
,,
,
故选:.
先把被开方数分解因式,再化简求值.
本题考查二次根式的性质与化简,掌握完全平方公式的特点是解题的关键.
8.【答案】
【解析】解:设平均每天票房的增长率为,
根据题意得:.
故选:.
第一天为,根据增长率为,得出第二天为,第三天为,根据三天累计为,即可得出关于的一元二次方程.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
9.【答案】
【解析】解:连接,延长交于,连接,
四边形是正方形,
,,,
,,
为的中点,
,
在和中,
,
≌,
,,
,
点为的中点,
,
为的中点,
,
,
,
故选:.
连接,延长交于,连接,由正方形推出,,,证得≌,得到,,根据三角形中位线定理得到,由勾股定理求出即可得到.
本题主要考查了正方形的性质,全等三角形的性质和判定,勾股定理,三角形的中位线定理,正确作出辅助线且证出是解决问题的关键.
10.【答案】
【解析】解:过点作于,过点作于,如图,
由题意得,,,
四边形为平行四边形,
,
,
四边形为菱形,
四边形的面积,
、的长度是关于的一元二次方程的两个实数根,
,
四边形的面积
故选:.
过点作于,过点作于,如图,利用纸条等宽得到,,,则可判断四边形为平行四边形,接着利用面积法得到,于是可判断四边形为菱形,利用菱形的面积公式得到四边形的面积,然后根据根与系数的关系进行判断.
本题考查了根与系数的关系:若,是一元二次方程的两根时,,也考查了菱形的判定与性质.
11.【答案】
【解析】解:四边形为矩形,点的坐标为,
,,
矩形与矩形是位似图形,
,,
∽,∽,
,,
,,
解得:,,
点的坐标为,
故选:.
根据位似图形的概念得到,,进而证明∽,∽,根据相似三角形的性质求出,得到答案.
本题考查的是位似图形的概念、相似三角形的性质,根据位似图形的概念得出,是解题的关键.
12.【答案】
【解析】解:连接交于点,连接,,
四边形是菱形,
对角线所在直线是其一条对称轴,点,点关于直线对称,
,
是的中点,
,
的周长,
要求的周长的最小值可先求出的最小值即可,
而的最小值就是的长,
过点作,交的延长线于点,
四边形是菱形,
,
,
在中,
,,
在中,
,,
,
的周长的最小值为,
故选:.
首先确定出的周长的最小值就是的最小值,然后利用将军饮马问题的模型构造出的周长的最小值,再利用勾股定理求出,进而解决问题.
本题考查轴对称最短路线问题,菱形的性质,勾股定理,特殊值的三角函数,掌握相关图形的性质和构造出最短路线是解题的关键.
13.【答案】
【解析】解:关于的方程有实数根,
当时,,
,
且,
当时,
此时方程为,满足题意,
故答案为:.
根据一元二次方程的根的判别式即可求出答案.
本题考查一元二次方程,解题的关键是正确理解根的判别式,本题属于基础题型.
14.【答案】或
【解析】
【分析】
把点的横纵坐标分别乘以或即可得到点的坐标.
本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形中对应点的坐标的比等于或.
【解答】
解:位似中心为原点,相似比为,
点的对应点的坐标为或,即或.
故答案为或.
15.【答案】
【解析】解:,,
;
故答案为:.
先把要求的式子变形为,再代入计算即可.
此题考查了二次根式的化简求值,用到的知识点是平方差公式、因式分解,关键是通过因式分解把要求的式子进行变形.
16.【答案】
【解析】解:如图,延长交射线于,
、分别是、的中点,
,
,
是的平分线,
,
,
,
,
,
,
由得,∽,
,
,
即.
故答案为:.
延长交射线于,根据三角形的中位线平行于第三边可得,根据两直线平行,内错角相等可得,再根据角平分线的定义可得,从而得到,根据等角对等边可得,求出,再根据,求出,然后根据和相似,利用相似三角形对应边成比例列式求解即可.
本题考查了三角形中位线定理、相似三角形的判定与性质,角平分线的定义,平行线的性质,延长构造出相似三角形,求出并得到相似三角形是解题的关键,也是本题的难点.
17.【答案】
【解析】解:四边形是菱形,
,,,
在中,,
,
,
根据菱形的面积公式可得,利用勾股定理求出即可.
本题考查菱形的性质、勾股定理等知识,解题的关键是利用菱形的两种面积公式,构建方程解决问题.
18.【答案】
【解析】
【分析】
利用分式的加减法则分别求得,,,即可求解.
本题考查了分式的加减法,找出其中的规律是解本题的关键.
【解答】
解:,
,
,
,
,
故答案为.
19.【答案】解:原式
;
原式
.
【解析】先根据二次根式的乘法法则和零次幂的运算法则进行计算,再合并同类二次根式即可;
先根据平方差公式、二次根式的性质、完全平方公式进行计算,再合并同类二次根式即可.
本题主要考查二次根式的混合运算、零指数幂,熟练掌握二次根式的运算法则、平方差公式、完全平方公式是解题关键.
20.【答案】解:,
,
,
,
,
,
或,
,;
,
,
,
,
,.
【解析】利用解一元二次方程配方法,进行计算即可解答;
利用解一元二次方程因式分解法,进行计算即可解答.
本题考查了解一元二次方程配方法,因式分解法,熟练掌握解一元二次方程的方法是解题的关键.
21.【答案】证明:,,
∽;
解:,
::,
又,
∽,
,
,
,
,
,,
,
,
,
.
【解析】根据,即可得出结论;
先由得::,再根据可判定和相似,进而得,然后由得,据此可得出,然后利用三角形的内角和定理可求出,进而可求出的度数.
此题主要考查了相似三角形的判定和性质,等腰三角形的性质,三角形的内角和定理,解答此题的关键是理解两个角对应相等的两个三角形相似;两边对应成比例,且夹角相等的两个三角形相似;相似三角形的对应边成比例、对应角相等.
22.【答案】解:设米,米.
,
∽
,
,
,,
∽,
,
,
,
解得:,
把代入中,得,
树的高度为米.
【解析】根据题意得出∽,利用相似三角形的性质得出,的长进而得出答案.
此题主要考查了相似三角形的应用,正确应用相似三角形的判定与性质是解题关键.
23.【答案】解:证明:如图,
在中,点是的中点,
,
,
,,
≌,
,
四边形是平行四边形,
又,点是的中点,即垂直平分,
,
平行四边形是菱形.
如图,过点作于点,
由知四边形是菱形,又,,
,,,
,
,
,
,
,,
,
,
,
.
【解析】由题意可得≌,则,根据“一组对边平行且相等的四边形是平行四边形”可得四边形是平行四边形;又垂直平分,根据垂直平分线的性质可得,根据“有一组临边相等的平行四边形是菱形”可得结论;
过点作于点,根据题意可得,,则,.
本题主要考查菱形的性质与判定,含角的直角三角形的三边关系,等腰直角三角形的性质与判定等内容,根据,等特殊角作出正确的垂线是解题关键.
24.【答案】解:设平均每年下降的百分率为,
依题意,得.
解得,不合题意,舍去.
答:平均每年下降的百分率为.
设单价应降低元,则每个的销售利润为元,每天可售出个,
依题意得:.
整理,得.
解得,.
为了减少库存,
,
答:单价应降低元.
【解析】设平均每年下降的百分率为,利用年该类电脑显卡的出厂价年该类电脑显卡的出厂价下降率,即可得出关于的一元二次方程,解之取其符合题意的值即可得出结论;
设单价应降低元,则每个的销售利润为元,每天可售出个,利用每天销售该电脑显卡获得的利润每个的销售利润日销售量,即可得出关于的一元二次方程,解之即可得出的值即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
25.【答案】证明:四边形是正方形,
,,
,
平分,
,
∽.
解:结论:是等腰三角形.
理由:四边形是正方形,
,,
平分,
,
,,
,
是等腰三角形;
解:四边形是正方形,
,,
是等腰直角三角形;
,
∽,
,
,
,
.
【解析】证明两个角对应相等即可.
通过计算证明,推出.
证明,利用相似三角形的性质解决问题即可.
本题属于相似形综合题,考查了正方形的性质,等腰直角三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题.
26.【答案】解:如图,过点作的垂线,过点作的垂线,两垂线交于点,连接,
,
,
,
,
又,
∽,
,
又,
,
即,
∽,
,
,
,
在中,,
.
【解析】过点作的垂线,过点作的垂线,两垂线交于点,连接,证明∽,由相似三角形的性质得出,证明∽,得出,求出,由勾股定理求出,最后由直角三角形的性质可求出的长.
此题主要考查相似三角形的判定与性质,作出正确的辅助线是解题的关键.
第1页,共1页
同课章节目录
