2022-2023学年山东省日照市开发区七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年山东省日照市开发区七年级(下)期末数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 326.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 00:00:00 | ||
图片预览


文档简介
2022-2023学年山东省日照市开发区七年级(下)期末数学试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在,,,,这五个数中,无理数的个数是( )
A. B. C. D.
2. 下列变形错误的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
3. 下列调查中,最适合采用全面调查方式的是( )
A. 调查某品牌洗衣机的使用寿命
B. 调查自贡市五一期间进出主城区的车流量
C. 调查某批次烟花爆竹的燃放效果
D. 调查自贡市某校七年级一班学生的睡眠时间
4. 下列说法不正确的是( )
A. 过任意一点可作已知直线的一条平行线
B. 连接直线外一点与直线上各点的所有线段中,垂线段最短
C. 在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D. 在同一平面内,平行于同一直线的两直线平行
5. 将点向右平移个单位,向上平移个单位,得到点的对应点的坐标是( )
A. B. C. D.
6. 如图,直线,将一个直角三角尺按如图所示的位置摆放,若,则的度数为( )
A.
B.
C.
D.
7. 在平面直角坐标系中,点的坐标为,平行于轴,若,则点的坐标为( )
A. B. C. 或 D. 或
8. 关于,的方程组的解满足,则的值为( )
A. B. C. D.
9. 某商店将某种碳酸饮料每瓶的价格下调了将某种果汁饮料每瓶的价格上调了,已知调价前买这两种饮料各一瓶共花费元,调价后买上述碳酸饮料瓶和果汁饮料瓶共花费元,若设上述碳酸饮料、果汁饮料在调价前每瓶分别为元和元,则可列方程组为( )
A. B.
C. D.
10. 若关于的不等式组只有个整数解,则的取值范围是( )
A. B. C. D.
11. 如图,,则下列各式中正确的是( )
A. B.
C. D.
12. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点,第次接着运动到点,第次接着运动到点,,按这样的运动规律,经过第次运动后,动点的坐标是( )
A. B. C. D.
二、填空题(本大题共4小题,共12.0分)
13. 的平方根是______ .
14. 在平面直角坐标系中,点到轴的距离为,则的值为______ .
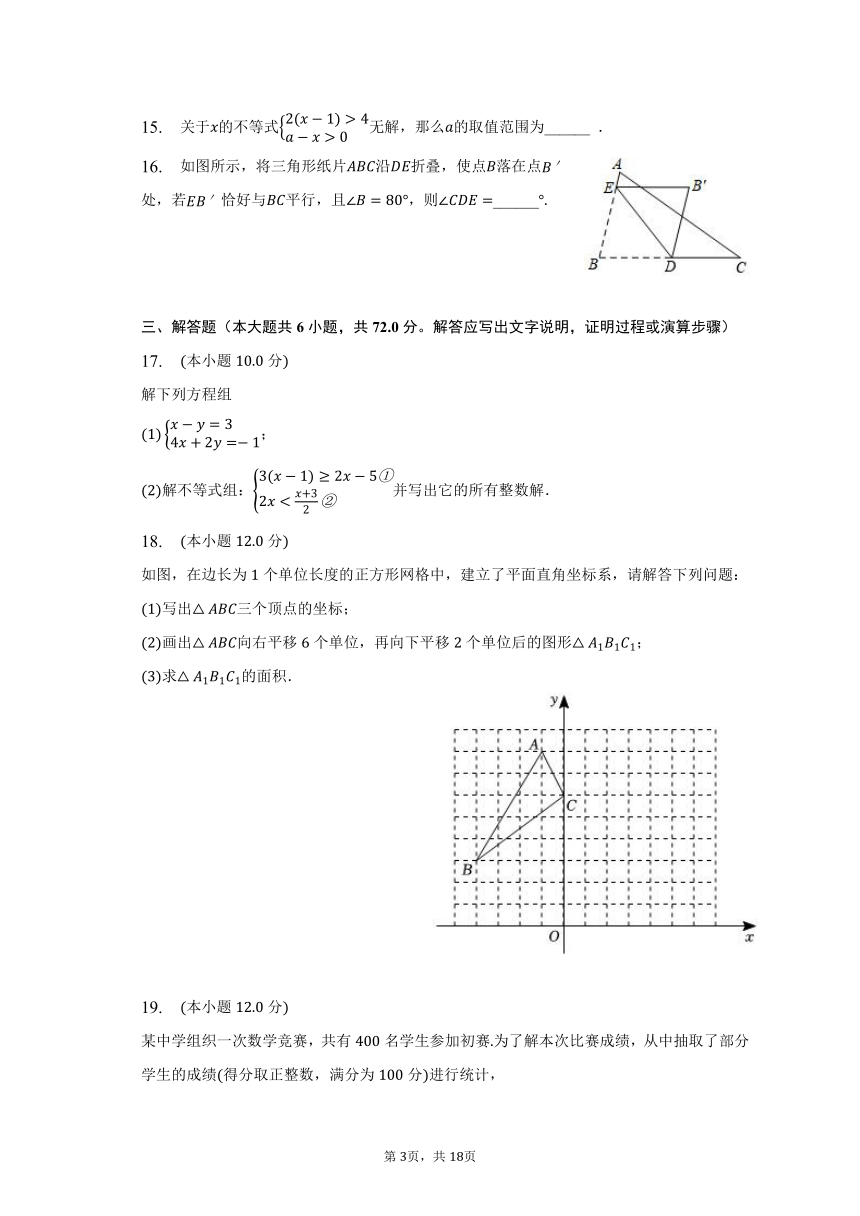
15. 关于的不等式无解,那么的取值范围为______ .
16. 如图所示,将三角形纸片沿折叠,使点落在点处,若恰好与平行,且,则______
三、解答题(本大题共6小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
解下列方程组
;
解不等式组:并写出它的所有整数解.
18. 本小题分
如图,在边长为个单位长度的正方形网格中,建立了平面直角坐标系,请解答下列问题:
写出三个顶点的坐标;
画出向右平移个单位,再向下平移个单位后的图形;
求的面积.
19. 本小题分
某中学组织一次数学竞赛,共有名学生参加初赛为了解本次比赛成绩,从中抽取了部分学生的成绩得分取正整数,满分为分进行统计,
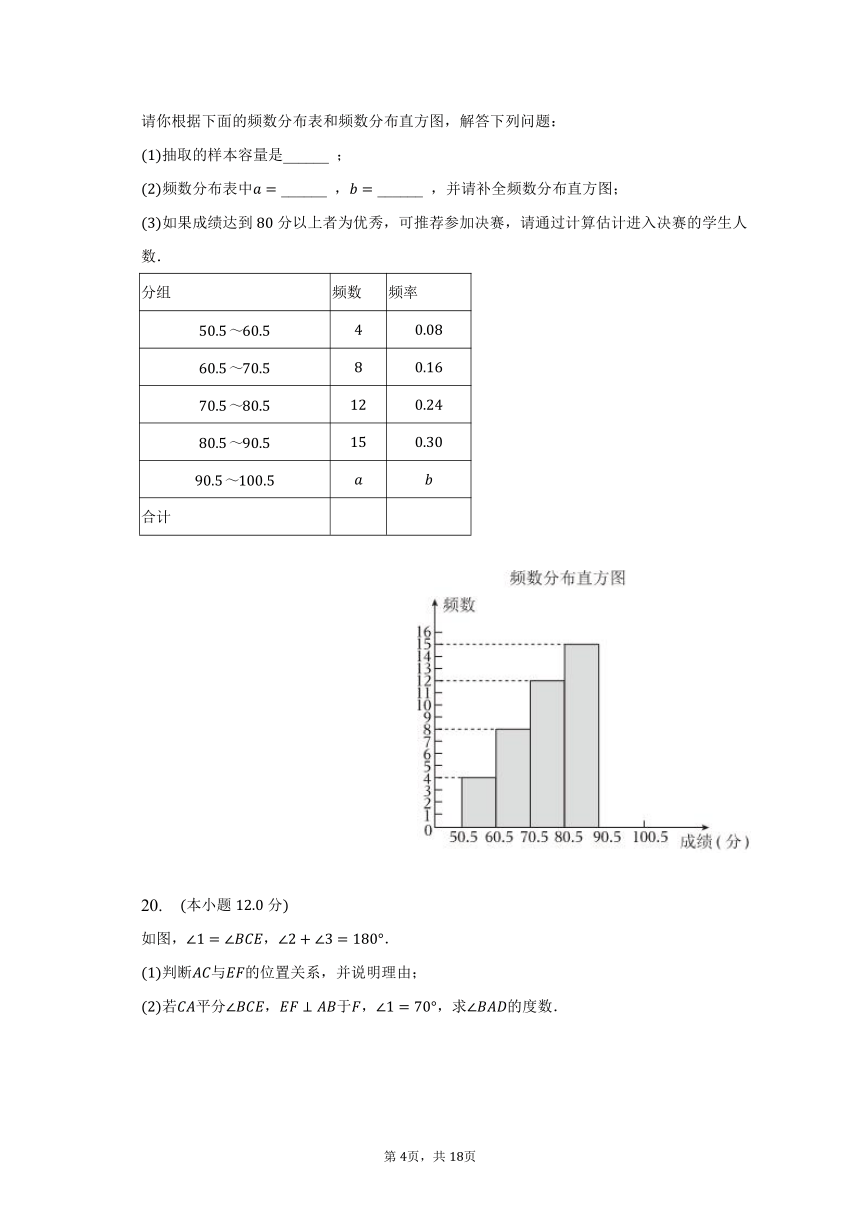
请你根据下面的频数分布表和频数分布直方图,解答下列问题:
抽取的样本容量是______ ;
频数分布表中 ______ , ______ ,并请补全频数分布直方图;
如果成绩达到分以上者为优秀,可推荐参加决赛,请通过计算估计进入决赛的学生人数.
分组 频数 频率
合计
20. 本小题分
如图,,.
判断与的位置关系,并说明理由;
若平分,于,,求的度数.
21. 本小题分
某校注重电化教学,为提高教学质量,要购进一批多媒体设备,了解到某商场销售,两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示.
进价万元套
售价万元套
若该商场计划购进两种多媒体教学设备若干套,共需万元,全部销售后可获毛利润万元则该商场计划购进,两种品牌的多媒体教学设备各多少套?
通过市场调研,该商场决定在中所购总数量不变的基础上,减少种设备的购进数量,增加种设备的购进数量若该校用于购进这两种多媒体教学设备的总资金不超过万元,且全部销售后可获毛利润不少于万元问有几种购买方案?并写出购买方案.
在学校购买多媒体设备可选方案中,选哪种方案商场获得利润最高,最高利润为多少万元?
22. 本小题分
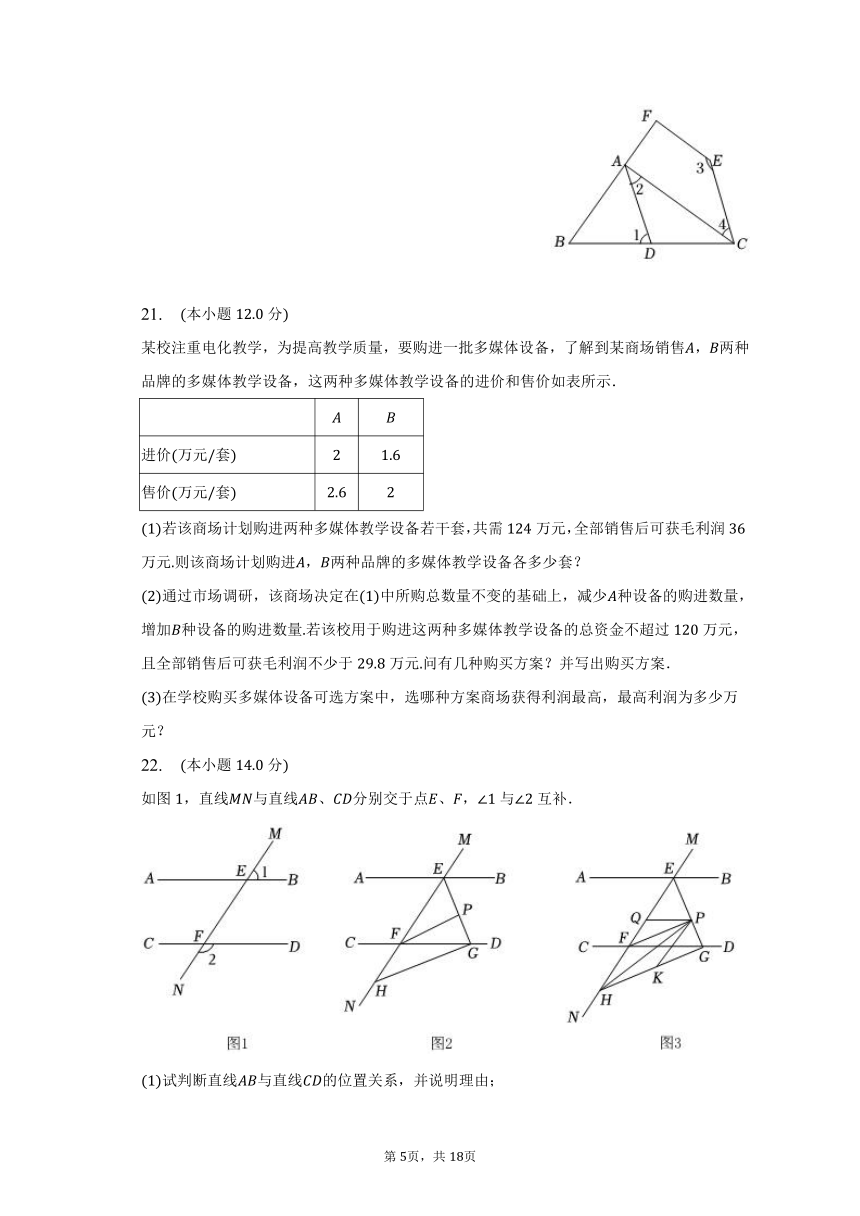
如图,直线与直线、分别交于点、,与互补.
试判断直线与直线的位置关系,并说明理由;
如图,与的角平分线交于点,与交于点,点是上一点,且,求证:.
如图,在的条件下,连接,是上一点使,作平分,问的大小是否发生变化?请说明理由.
答案和解析
1.【答案】
【解析】解:是有限小数,因此是有理数;
是分数,因此是有理数;
是开方开不尽的数,故是无理数;
,它是一个有理数;
是无限不循环小数,故是无理数.
所以一共有个无理数.
故选B.
根据有理数和无理数的概念来确定即可求解.
此题主要考查了无理数的定义,要注意带根号的数与无理数的区别:带根号的数不一定是无理数,带根号且开方开不尽的数一定是无理数.本题中是有理数中的整数.
2.【答案】
【解析】解:、若,则,故A不符合题意;
B、若,则,故B不符合题意;
C、若,则,即,故C符合题意;
D、若,则,故D不符合题意;
故选:.
根据不等式的性质进行计算,逐一判断即可解答.
本题考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
3.【答案】
【解析】解:、调查某品牌洗衣机的使用寿命,适合抽样调查,选项不符合题意;
B、调查自贡市五一期间进出主城区的车流量,适合抽样调查,选项不符合题意;
C、调查某批次烟花爆竹的燃放效果,适合抽样调查,选项不符合题意;
D、调查自贡市某校七年级一班学生的睡眠时间,适合全面调查,故选项符合题意.
故选:.
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而且抽样调查得到的调查结果不准确,只是近似值.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.【答案】
【解析】解:过直线外的任意一点可作已知直线的一条平行线,原说法错误,故本选项不符合题意;
B.连接直线外一点与直线上各点的所有线段中,垂线段最短,说法正确,故本选项符合题意;
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直,说法正确,故本选项符合题意;
D.在同一平面内,平行于同一直线的两直线平行,说法正确,故本选项符合题意.
故选:.
选项A根据平行公理判断即可;选项B根据垂线段的性质判断即可;选项C根据垂线的定义判断即可;选项D根据平行线的判定方法判断即可.
本题考查了平行线的性质与判断,垂线段最短以及平行公理及推动,掌握相关定理与公理是解答本题的关键.
5.【答案】
【解析】解:将向右平移个单位,向上平移个单位得到对应点,
的坐标为,
即,
故选:.
根据向右移动,横坐标加,纵坐标不变,即可得到点的对应点的坐标.
本题考查了坐标与图形变化平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解决问题的关键.
6.【答案】
【解析】解:如图,
过点作,
,
,
,
,,
,
,
故选:.
先利用平行线的性质得出,进而利用三角板的特征求出,最后利用平行线的性质即可.
本题主要考查了平行线的性质,角度的计算,解本题的关键是正确作出辅助线.
7.【答案】
【解析】解:轴,
、两点纵坐标都为,
又,
当点在点左边时,,
当点在点右边时,;
故选:.
线段轴,、两点纵坐标相等,又,点可能在点左边或者右边,根据距离确定点坐标.
本题考查了平行于轴的直线上的点纵坐标相等,再根据两点相对的位置及两点距离确定点的坐标.
8.【答案】
【解析】解:,
,
,
,
,
,
故选C.
把方程组的两个方程相加,得到,结合,即可求出的值.
本题主要考查了二元一次方程组的解得知识点,解答本题的关键是把方程组的两个方程相加得到,与的一个关系式,此题基础题.
9.【答案】
【解析】解:设上述碳酸饮料、果汁饮料在调价前每瓶分别为元和元,
由题意得,.
故选:.
设上述碳酸饮料、果汁饮料在调价前每瓶分别为元和元,根据调价前买这两种饮料各一瓶共花费元,调价后买上述碳酸饮料瓶和果汁饮料瓶共花费元,列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
10.【答案】
【解析】解:,
解得,
解得,
所以不等式组的解集为,
因为不等式组只有个整数解,
所以,
所以.
故选:.
先解不等式组得到,再利用不等式组只有个整数解,则只能取、、、,所以,然后解关于的不等式组即可.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
11.【答案】
【解析】解:延长,
,
,
与互补,
,
,
,即,
.
故选D.
延长,由可知,,再由三角形内角和及邻补角定义即可得出结论.
本题考查的是平行线的性质及三角形内角和及邻补角定义,根据题意作出辅助线,构造出三角形,利用三角形内角和及邻补角定义求解是解答此题的关键.
12.【答案】
【解析】解:根据动点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点,
第次接着运动到点,第次接着运动到点,
第次运动到点,第次接着运动到点,,
横坐标为运动次数的倍,经过第次运动后,动点的横坐标为,
纵坐标为,,,,每次一轮,
经过第次运动后,,
故动点的纵坐标为,
经过第次运动后,动点的坐标是.
故选:.
根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数的倍,纵坐标为,,,,每次一轮这一规律,进而求出即可.
此题主要考查了点的坐标规律,培养学生观察和归纳能力,从所给的数据和图形中寻求规律进行解题是解答本题的关键.
13.【答案】
【解析】解:,
,
的平方根是.
故答案为:.
直接根据平方根的定义即可求解.
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;的平方根是;负数没有平方根.
14.【答案】或
【解析】解:点到轴的距离为,
,
解得或.
故答案为:或.
根据点到轴的距离等于横坐标的绝对值列出方程,然后求解即可.
此题考查的是点的坐标,掌握点的坐标的定义是解决此题的关键.
15.【答案】
【解析】解:由得:,
由得:,
不等式组的无解,
,
故答案为:.
分别求出每一个不等式的解集,根据不等式组的解集可得答案.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
16.【答案】
【解析】解:因为三角形纸片沿折叠,得到三角形,
所以,,
因为,
所以,
所以,
所以,
因为,
所以.
故答案为:.
根据折叠,平行线的性质,利用平角的定义求解即可.
本题考查的是平行线的性质、折叠,解题的关键是熟练掌握平行线的性质、折叠的特点,以及平角的定义.
17.【答案】解:,
,得:,
解得,
将代入得:,
解得,
方程组的解为;
解不等式得:,
解不等式得:,
则不等式组的解集为,
所以不等式组的整数解为、、.
【解析】利用加减消元法求解即可;
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
本题考查的是解二元一次方程组和一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
18.【答案】解:,,;
如图所示:,即为所求;
的面积为:.
【解析】直接利用已知坐标系得出各点坐标即可;
直接利用平移的性质得出对应点位置进而得出答案;
利用所在矩形面积减去周围三角形面积进而得出答案.
此题主要考查了作图平移变换以及三角形面积求法,正确得出对应点位置是解题关键.
19.【答案】
【解析】解:人,
故答案为:;
,,
故答案为:,,
补全频数分布直方图如图所示;
人,
答:估计进入决赛的学生人数有人.
根据每组的频数、频率所对应的数据,可求出样本容量;
根据频数之和等于样本容量,频率之和为,可求出、的值;
求出样本中“优秀”所占的百分比即可求出答案.
本题考查频数分布表、频数分布直方图,掌握频数、频率、总数之间的关系是正确解答的关键.
20.【答案】解:理由如下:
,
,
,
,
,
;
,平分,
,
,,
,
,于,
,
.
【解析】由,可得到直线与平行,可得到与间关系,再由判断与的位置关系;
由的结论及垂直可得到的度数,再由平行线及角平分线的性质得到的度数,利用角的和差关系可得结论.
本题考查了平行线的性质和判定、角平分线的性质及垂直的性质等知识点,综合性较强,掌握平行线的性质和判定是解决本题的关键.
21.【答案】解:设该商场计划购进种品牌的多媒体教学设备套、种品牌的多媒体教学设备套.
根据题意得,解得.
该商场计划购进种品牌的多媒体教学设备套、种品牌的多媒体教学设备套.
设购进种设备套,那么种设备套.
根据题意得,解得.
可取个整数值,共种购买方案,分别为:
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套.
设购进种设备套,那么种设备套.
根据题意,获得的利润为.
随的增大而增大,
当时,最大,.
在学校购买多媒体设备可选方案中,购进种设备套,种设备套商场获得利润最高,最高利润为万元.
【解析】设该商场计划购进种品牌的多媒体教学设备套、种品牌的多媒体教学设备套,根据题意列二元一次方程组并求解即可;
设购进种设备套,那么种设备套,根据题意列一元一次不等式组并求解.可取多少个整数值,就有多少种购买方案,分别将它们写出来即可;
设购进种设备套,那么种设备套.根据题意得利润关于的表达式,根据该表达式的值随的变化特点,求出当取何值时利润最高及其最大值.
本题考查一次函数、二元一次方程组和一元一次不等式组的应用,难度不大,但过程繁杂,一定要认真、细致,确保计算正确无误.
22.【答案】解:,
理由如下:
与互补,
,
又,,
,
;
由知,,
.
又与的角平分线交于点,
,
,即.
,
;
没发生变化,理由:
,
.
又,
.
.
平分,
.
.
答:的度数为.
【解析】根据同旁内角互补,两条直线平行即可判断直线与直线平行;
先根据两条直线平行,同旁内角互补,再根据与的角平分线交于点,可得,进而证明;
根据角平分线定义,及角的和差计算即可求得的度数.
本题考查了平行线的判定和性质、余角和补角,解决本题的关键是综合运用角平分线的定义、平行线的性质、余角和补角.
第1页,共1页
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在,,,,这五个数中,无理数的个数是( )
A. B. C. D.
2. 下列变形错误的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
3. 下列调查中,最适合采用全面调查方式的是( )
A. 调查某品牌洗衣机的使用寿命
B. 调查自贡市五一期间进出主城区的车流量
C. 调查某批次烟花爆竹的燃放效果
D. 调查自贡市某校七年级一班学生的睡眠时间
4. 下列说法不正确的是( )
A. 过任意一点可作已知直线的一条平行线
B. 连接直线外一点与直线上各点的所有线段中,垂线段最短
C. 在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D. 在同一平面内,平行于同一直线的两直线平行
5. 将点向右平移个单位,向上平移个单位,得到点的对应点的坐标是( )
A. B. C. D.
6. 如图,直线,将一个直角三角尺按如图所示的位置摆放,若,则的度数为( )
A.
B.
C.
D.
7. 在平面直角坐标系中,点的坐标为,平行于轴,若,则点的坐标为( )
A. B. C. 或 D. 或
8. 关于,的方程组的解满足,则的值为( )
A. B. C. D.
9. 某商店将某种碳酸饮料每瓶的价格下调了将某种果汁饮料每瓶的价格上调了,已知调价前买这两种饮料各一瓶共花费元,调价后买上述碳酸饮料瓶和果汁饮料瓶共花费元,若设上述碳酸饮料、果汁饮料在调价前每瓶分别为元和元,则可列方程组为( )
A. B.
C. D.
10. 若关于的不等式组只有个整数解,则的取值范围是( )
A. B. C. D.
11. 如图,,则下列各式中正确的是( )
A. B.
C. D.
12. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点,第次接着运动到点,第次接着运动到点,,按这样的运动规律,经过第次运动后,动点的坐标是( )
A. B. C. D.
二、填空题(本大题共4小题,共12.0分)
13. 的平方根是______ .
14. 在平面直角坐标系中,点到轴的距离为,则的值为______ .
15. 关于的不等式无解,那么的取值范围为______ .
16. 如图所示,将三角形纸片沿折叠,使点落在点处,若恰好与平行,且,则______
三、解答题(本大题共6小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
解下列方程组
;
解不等式组:并写出它的所有整数解.
18. 本小题分
如图,在边长为个单位长度的正方形网格中,建立了平面直角坐标系,请解答下列问题:
写出三个顶点的坐标;
画出向右平移个单位,再向下平移个单位后的图形;
求的面积.
19. 本小题分
某中学组织一次数学竞赛,共有名学生参加初赛为了解本次比赛成绩,从中抽取了部分学生的成绩得分取正整数,满分为分进行统计,
请你根据下面的频数分布表和频数分布直方图,解答下列问题:
抽取的样本容量是______ ;
频数分布表中 ______ , ______ ,并请补全频数分布直方图;
如果成绩达到分以上者为优秀,可推荐参加决赛,请通过计算估计进入决赛的学生人数.
分组 频数 频率
合计
20. 本小题分
如图,,.
判断与的位置关系,并说明理由;
若平分,于,,求的度数.
21. 本小题分
某校注重电化教学,为提高教学质量,要购进一批多媒体设备,了解到某商场销售,两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示.
进价万元套
售价万元套
若该商场计划购进两种多媒体教学设备若干套,共需万元,全部销售后可获毛利润万元则该商场计划购进,两种品牌的多媒体教学设备各多少套?
通过市场调研,该商场决定在中所购总数量不变的基础上,减少种设备的购进数量,增加种设备的购进数量若该校用于购进这两种多媒体教学设备的总资金不超过万元,且全部销售后可获毛利润不少于万元问有几种购买方案?并写出购买方案.
在学校购买多媒体设备可选方案中,选哪种方案商场获得利润最高,最高利润为多少万元?
22. 本小题分
如图,直线与直线、分别交于点、,与互补.
试判断直线与直线的位置关系,并说明理由;
如图,与的角平分线交于点,与交于点,点是上一点,且,求证:.
如图,在的条件下,连接,是上一点使,作平分,问的大小是否发生变化?请说明理由.
答案和解析
1.【答案】
【解析】解:是有限小数,因此是有理数;
是分数,因此是有理数;
是开方开不尽的数,故是无理数;
,它是一个有理数;
是无限不循环小数,故是无理数.
所以一共有个无理数.
故选B.
根据有理数和无理数的概念来确定即可求解.
此题主要考查了无理数的定义,要注意带根号的数与无理数的区别:带根号的数不一定是无理数,带根号且开方开不尽的数一定是无理数.本题中是有理数中的整数.
2.【答案】
【解析】解:、若,则,故A不符合题意;
B、若,则,故B不符合题意;
C、若,则,即,故C符合题意;
D、若,则,故D不符合题意;
故选:.
根据不等式的性质进行计算,逐一判断即可解答.
本题考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
3.【答案】
【解析】解:、调查某品牌洗衣机的使用寿命,适合抽样调查,选项不符合题意;
B、调查自贡市五一期间进出主城区的车流量,适合抽样调查,选项不符合题意;
C、调查某批次烟花爆竹的燃放效果,适合抽样调查,选项不符合题意;
D、调查自贡市某校七年级一班学生的睡眠时间,适合全面调查,故选项符合题意.
故选:.
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而且抽样调查得到的调查结果不准确,只是近似值.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.【答案】
【解析】解:过直线外的任意一点可作已知直线的一条平行线,原说法错误,故本选项不符合题意;
B.连接直线外一点与直线上各点的所有线段中,垂线段最短,说法正确,故本选项符合题意;
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直,说法正确,故本选项符合题意;
D.在同一平面内,平行于同一直线的两直线平行,说法正确,故本选项符合题意.
故选:.
选项A根据平行公理判断即可;选项B根据垂线段的性质判断即可;选项C根据垂线的定义判断即可;选项D根据平行线的判定方法判断即可.
本题考查了平行线的性质与判断,垂线段最短以及平行公理及推动,掌握相关定理与公理是解答本题的关键.
5.【答案】
【解析】解:将向右平移个单位,向上平移个单位得到对应点,
的坐标为,
即,
故选:.
根据向右移动,横坐标加,纵坐标不变,即可得到点的对应点的坐标.
本题考查了坐标与图形变化平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解决问题的关键.
6.【答案】
【解析】解:如图,
过点作,
,
,
,
,,
,
,
故选:.
先利用平行线的性质得出,进而利用三角板的特征求出,最后利用平行线的性质即可.
本题主要考查了平行线的性质,角度的计算,解本题的关键是正确作出辅助线.
7.【答案】
【解析】解:轴,
、两点纵坐标都为,
又,
当点在点左边时,,
当点在点右边时,;
故选:.
线段轴,、两点纵坐标相等,又,点可能在点左边或者右边,根据距离确定点坐标.
本题考查了平行于轴的直线上的点纵坐标相等,再根据两点相对的位置及两点距离确定点的坐标.
8.【答案】
【解析】解:,
,
,
,
,
,
故选C.
把方程组的两个方程相加,得到,结合,即可求出的值.
本题主要考查了二元一次方程组的解得知识点,解答本题的关键是把方程组的两个方程相加得到,与的一个关系式,此题基础题.
9.【答案】
【解析】解:设上述碳酸饮料、果汁饮料在调价前每瓶分别为元和元,
由题意得,.
故选:.
设上述碳酸饮料、果汁饮料在调价前每瓶分别为元和元,根据调价前买这两种饮料各一瓶共花费元,调价后买上述碳酸饮料瓶和果汁饮料瓶共花费元,列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
10.【答案】
【解析】解:,
解得,
解得,
所以不等式组的解集为,
因为不等式组只有个整数解,
所以,
所以.
故选:.
先解不等式组得到,再利用不等式组只有个整数解,则只能取、、、,所以,然后解关于的不等式组即可.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
11.【答案】
【解析】解:延长,
,
,
与互补,
,
,
,即,
.
故选D.
延长,由可知,,再由三角形内角和及邻补角定义即可得出结论.
本题考查的是平行线的性质及三角形内角和及邻补角定义,根据题意作出辅助线,构造出三角形,利用三角形内角和及邻补角定义求解是解答此题的关键.
12.【答案】
【解析】解:根据动点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点,
第次接着运动到点,第次接着运动到点,
第次运动到点,第次接着运动到点,,
横坐标为运动次数的倍,经过第次运动后,动点的横坐标为,
纵坐标为,,,,每次一轮,
经过第次运动后,,
故动点的纵坐标为,
经过第次运动后,动点的坐标是.
故选:.
根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数的倍,纵坐标为,,,,每次一轮这一规律,进而求出即可.
此题主要考查了点的坐标规律,培养学生观察和归纳能力,从所给的数据和图形中寻求规律进行解题是解答本题的关键.
13.【答案】
【解析】解:,
,
的平方根是.
故答案为:.
直接根据平方根的定义即可求解.
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;的平方根是;负数没有平方根.
14.【答案】或
【解析】解:点到轴的距离为,
,
解得或.
故答案为:或.
根据点到轴的距离等于横坐标的绝对值列出方程,然后求解即可.
此题考查的是点的坐标,掌握点的坐标的定义是解决此题的关键.
15.【答案】
【解析】解:由得:,
由得:,
不等式组的无解,
,
故答案为:.
分别求出每一个不等式的解集,根据不等式组的解集可得答案.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
16.【答案】
【解析】解:因为三角形纸片沿折叠,得到三角形,
所以,,
因为,
所以,
所以,
所以,
因为,
所以.
故答案为:.
根据折叠,平行线的性质,利用平角的定义求解即可.
本题考查的是平行线的性质、折叠,解题的关键是熟练掌握平行线的性质、折叠的特点,以及平角的定义.
17.【答案】解:,
,得:,
解得,
将代入得:,
解得,
方程组的解为;
解不等式得:,
解不等式得:,
则不等式组的解集为,
所以不等式组的整数解为、、.
【解析】利用加减消元法求解即可;
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
本题考查的是解二元一次方程组和一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
18.【答案】解:,,;
如图所示:,即为所求;
的面积为:.
【解析】直接利用已知坐标系得出各点坐标即可;
直接利用平移的性质得出对应点位置进而得出答案;
利用所在矩形面积减去周围三角形面积进而得出答案.
此题主要考查了作图平移变换以及三角形面积求法,正确得出对应点位置是解题关键.
19.【答案】
【解析】解:人,
故答案为:;
,,
故答案为:,,
补全频数分布直方图如图所示;
人,
答:估计进入决赛的学生人数有人.
根据每组的频数、频率所对应的数据,可求出样本容量;
根据频数之和等于样本容量,频率之和为,可求出、的值;
求出样本中“优秀”所占的百分比即可求出答案.
本题考查频数分布表、频数分布直方图,掌握频数、频率、总数之间的关系是正确解答的关键.
20.【答案】解:理由如下:
,
,
,
,
,
;
,平分,
,
,,
,
,于,
,
.
【解析】由,可得到直线与平行,可得到与间关系,再由判断与的位置关系;
由的结论及垂直可得到的度数,再由平行线及角平分线的性质得到的度数,利用角的和差关系可得结论.
本题考查了平行线的性质和判定、角平分线的性质及垂直的性质等知识点,综合性较强,掌握平行线的性质和判定是解决本题的关键.
21.【答案】解:设该商场计划购进种品牌的多媒体教学设备套、种品牌的多媒体教学设备套.
根据题意得,解得.
该商场计划购进种品牌的多媒体教学设备套、种品牌的多媒体教学设备套.
设购进种设备套,那么种设备套.
根据题意得,解得.
可取个整数值,共种购买方案,分别为:
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套;
购进种设备套、种设备套.
设购进种设备套,那么种设备套.
根据题意,获得的利润为.
随的增大而增大,
当时,最大,.
在学校购买多媒体设备可选方案中,购进种设备套,种设备套商场获得利润最高,最高利润为万元.
【解析】设该商场计划购进种品牌的多媒体教学设备套、种品牌的多媒体教学设备套,根据题意列二元一次方程组并求解即可;
设购进种设备套,那么种设备套,根据题意列一元一次不等式组并求解.可取多少个整数值,就有多少种购买方案,分别将它们写出来即可;
设购进种设备套,那么种设备套.根据题意得利润关于的表达式,根据该表达式的值随的变化特点,求出当取何值时利润最高及其最大值.
本题考查一次函数、二元一次方程组和一元一次不等式组的应用,难度不大,但过程繁杂,一定要认真、细致,确保计算正确无误.
22.【答案】解:,
理由如下:
与互补,
,
又,,
,
;
由知,,
.
又与的角平分线交于点,
,
,即.
,
;
没发生变化,理由:
,
.
又,
.
.
平分,
.
.
答:的度数为.
【解析】根据同旁内角互补,两条直线平行即可判断直线与直线平行;
先根据两条直线平行,同旁内角互补,再根据与的角平分线交于点,可得,进而证明;
根据角平分线定义,及角的和差计算即可求得的度数.
本题考查了平行线的判定和性质、余角和补角,解决本题的关键是综合运用角平分线的定义、平行线的性质、余角和补角.
第1页,共1页
同课章节目录
