2022-2023学年云南省玉溪市峨山县重点学校九年级(下)期中考试数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年云南省玉溪市峨山县重点学校九年级(下)期中考试数学试卷(含解析) | 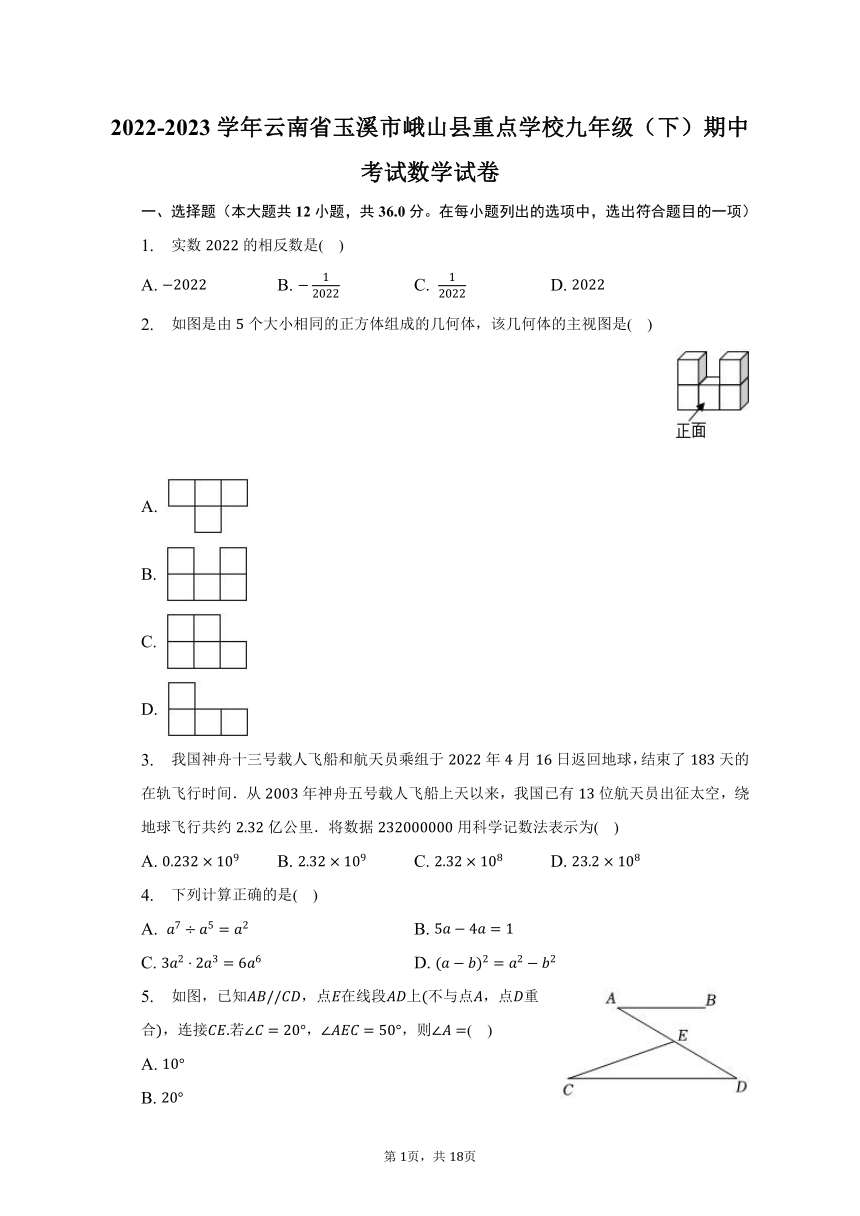 | |
| 格式 | docx | ||
| 文件大小 | 329.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 16:24:52 | ||
图片预览




文档简介
2022-2023学年云南省玉溪市峨山县重点学校九年级(下)期中考试数学试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 实数的相反数是( )
A. B. C. D.
2. 如图是由个大小相同的正方体组成的几何体,该几何体的主视图是( )
A.
B.
C.
D.
3. 我国神舟十三号载人飞船和航天员乘组于年月日返回地球,结束了天的在轨飞行时间.从年神舟五号载人飞船上天以来,我国已有位航天员出征太空,绕地球飞行共约亿公里.将数据用科学记数法表示为( )
A. B. C. D.
4. 下列计算正确的是( )
A. B.
C. D.
5. 如图,已知,点在线段上不与点,点重合,连接若,,则( )
A.
B.
C.
D.
6. 一个多边形的内角和为,则这个多边形是( )
A. 七边形 B. 八边形 C. 九边形 D. 十边形
7. 每年月日为“世界读书日”,读书能丰富知识,陶冶情操,提高文化底蕴.某中学七年级一班统计了今年月“书香校园”读书活动中,全班同学的每月课外阅读数量单位:本及阅读不同种类书目数量,并绘制了如图所示的统计图,下列说法正确的是( )
A. 平均每月课外阅读数量大于本
B. 表示阅读“文学类”书籍的扇形圆心角是
C. 的值为
D. 根据调查统计结果发现“科幻类”书籍深受该中学七年级一班学生喜爱
8. 一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 有一个实数根 D. 没有实数根
9. 探索规律:观察下面的一列单项式:、、、、、,根据其中的规律得出的第个单项式是( )
A. B. C. D.
10. 如图,在矩形中,若,,,则的长为( )
A.
B.
C.
D.
11. 如图,如果从半径为的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥接缝处不重叠,则这个圆锥的底面半径为( )
A. B. C. D.
12. 若关于的不等式组,的解集为,则的取值范围是( )
A. B. C. D.
二、填空题(本大题共4小题,共8.0分)
13. 在函数中,自变量的取值范围是______.
14. 因式分解:______.
15. 反比例函数的图象位于第二、四象限,函数图象上一点到轴,轴的距离分别为和,则的值为______ .
16. 如图,在中,按以下步骤作图:分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;作直线交边于点若,,,则的长为______ .
三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
计算:.
18. 本小题分
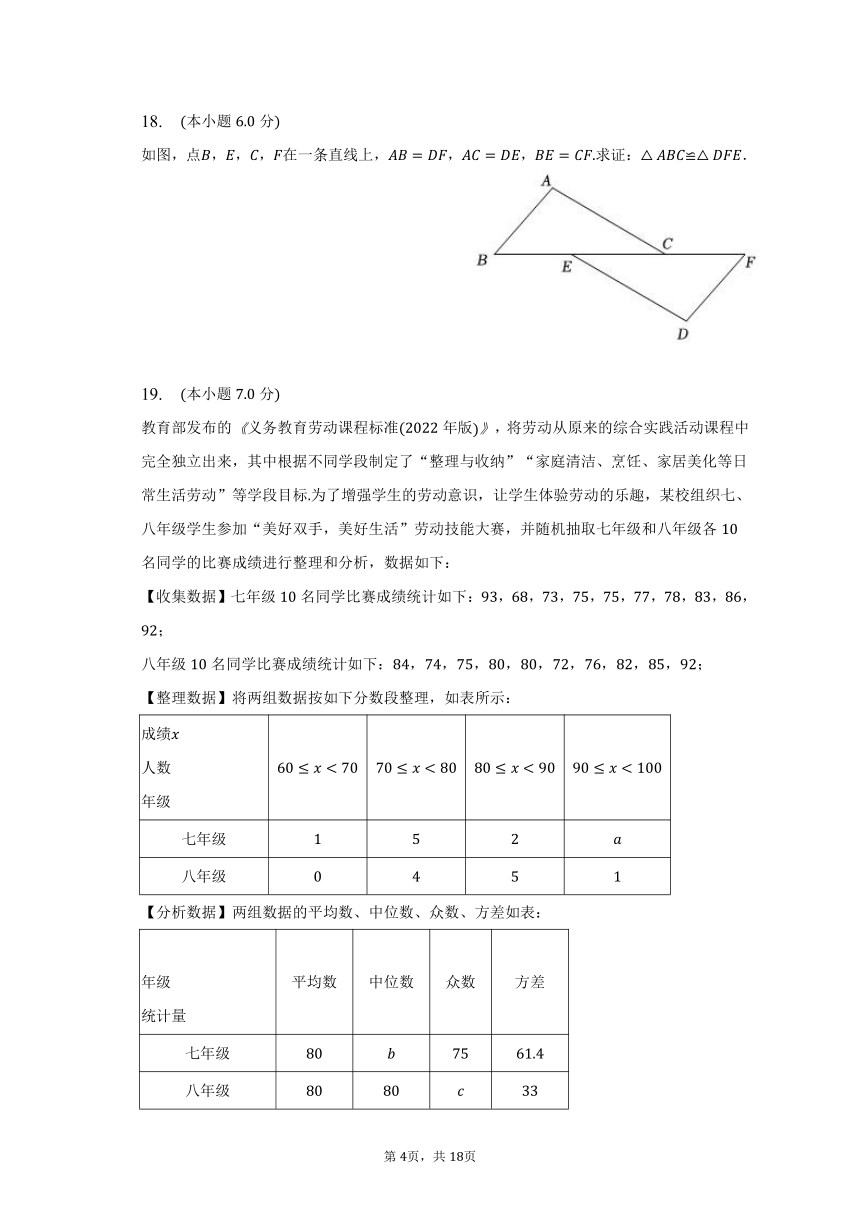
如图,点,,,在一条直线上,,,求证:≌.
19. 本小题分
教育部发布的义务教育劳动课程标准年版,将劳动从原来的综合实践活动课程中完全独立出来,其中根据不同学段制定了“整理与收纳”“家庭清洁、烹饪、家居美化等日常生活劳动”等学段目标为了增强学生的劳动意识,让学生体验劳动的乐趣,某校组织七、八年级学生参加“美好双手,美好生活”劳动技能大赛,并随机抽取七年级和八年级各名同学的比赛成绩进行整理和分析,数据如下:
【收集数据】七年级名同学比赛成绩统计如下:,,,,,,,,,;
八年级名同学比赛成绩统计如下:,,,,,,,,,;
【整理数据】将两组数据按如下分数段整理,如表所示:
成绩
人数
年级
七年级
八年级
【分析数据】两组数据的平均数、中位数、众数、方差如表:
年级
统计量 平均数 中位数 众数 方差
七年级
八年级
【问题解决】根据以上信息,解答下列问题:
填空: ______ , ______ , ______ ;
样本数据中,七年级小杨同学和八年级小吴同学的成绩都为分,则哪位同学的成绩在本年级排名更靠前,请说明理由.
20. 本小题分
某校准备从八年级班、班的团员中选取两名同学作为运动会的志愿者,已知班有名团员其中男生人,女生人班有名团员其中男生人,女生人.
如果从这两个班的全体团员中随机选取一名同学作为志愿者的组长,则这名同学是男生的概率为______;
如果分别从班、班的团员中随机各选取一人,请用画树状图或列表的方法求这两名同学恰好是一名男生、一名女生的概率.
21. 本小题分
已知:如图,在矩形中,对角线的垂直平分线与相交于点,与相交于点,连接,.
求证:四边形是菱形;
若,,求菱形的面积.
22. 本小题分
今年我市某公司分两次采购了一批土豆,第一次花费万元,第二次花费万元,已知第一次采购时每吨土豆的价格比去年的平均价格上涨了元,第二次采购时每吨土豆的价格比去年的平均价格下降了元,第二次的采购数量是第一次采购数量的倍.
问去年每吨土豆的平均价格是多少元?
该公司可将土豆加工成薯片或淀粉,因设备原因,两种产品不能同时加工,若单独加工成薯片,每天可加工吨土豆,每吨土豆获利元;若单独加工成淀粉,每天可加工吨土豆,每吨土豆获利元,由于出口需要,所有采购的土豆必须全部加工完且用时不超过天,其中加工成薯片的土豆数量不少于加工成淀粉的土豆数量的,为获得最大利润,应将多少吨土豆加工成薯片?最大利润是多少?
23. 本小题分
如图,四边形内接于,是的直径,,的延长线交于点,延长交于点,.
求证:是的切线;
连接,,,的长为______.
24. 本小题分
已知抛物线,,,为常数且.
若,则抛物线的对称轴为直线______ ;
在的条件下,抛物线过点,,,求的值.
答案和解析
1.【答案】
【解析】解:实数的相反数是,
故选:.
根据相反数的定义直接求解.
本题主要考查相反数的定义,熟练掌握相反数的定义是解答此题的关键.
2.【答案】
【解析】
【分析】
主视图是从物体前面看所得到的图形,据此判断即可.
【解答】
解:根据主视图的概念,可知该几何体的主视图为:
故选:.
【点评】
本题考查三视图,掌握三视图的概念是解题的关键.
3.【答案】
【解析】解:.
故选:.
用科学记数法表示较大的数时,一般形式为,其中,为整数,且比原来的整数位数少,据此判断即可.
此题主要考查了用科学记数法表示较大的数,一般形式为,其中,确定与的值是解题的关键.
4.【答案】
【解析】
【分析】
根据同底数幂的除法法则,合并同类项法则,单项式乘单项式法则和完全平方公式对每个选项的结论作出判断即可得出结论.
【解答】
解:,选项的计算正确;
,选项的计算不正确;
,选项的计算不正确;
,选项的计算不正确.
故选:.
【点评】
本题主要考查了同底数幂的除法法则,合并同类项法则,单项式乘单项式法则和完全平方公式,正确使用上述法则与公式进行运算是解题的关键.
5.【答案】
【解析】解:为的外角,且,,
,即,
,
,
.
故选:.
由为的外角,利用外角性质求出的度数,再利用两直线平行内错角相等即可求出的度数.
此题考查了平行线的性质,以及外角性质,熟练掌握平行线的性质是解本题的关键.
6.【答案】
【解析】解:设多边形的边数为,
,
解得:.
故选:.
根据多边形的内角和公式:列出方程,解方程即可得出答案.
本题考查了多边形的内角和,体现了方程思想,掌握多边形的内角和是解题的关键.
7.【答案】
【解析】解:、七年级一班同学的平均每月课外阅读数量为本本,故错误,不符合题意;
B、表示阅读“文学类”书籍的扇形圆心角为,故错误,不符合题意;
C、,故,故错误,不符合题意;
D、“科幻类”书籍所占的比例最大,故“科幻类”书籍深受该中学七年级一班学生喜爱,正确,符合题意.
故选:.
A、求出平均每月课外阅读数量为本,可判断选项错误;
B、表示阅读“文学类”书籍的扇形圆心角为,可判断选项错误;
C、根据扇形统计表中所有项目所占比例之和为可求出值不是,可判断选项错误;
D、根据“科幻类”书籍所占的比例最大,可直接判断正确.
本题考查了条形统计图,扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
8.【答案】
【解析】解:,
所以方程有两个相等的实数根.
故选:.
计算出判别式的值即可得出答案.
本题主要考查根的判别式,一元二次方程的根与有如下关系:
当时,方程有两个不相等的两个实数根;
当时,方程有两个相等的两个实数根;
当时,方程无实数根.
9.【答案】
【解析】解:根据题意得:
第个单项式是.
故选:.
根据符号的规律:为奇数时,单项式为正号,为偶数时,符号为负号;系数的绝对值的规律:第个对应的系数的绝对值是指数的规律:第个对应的指数是解答即可.
本题考查了单项式的知识,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.分别找出单项式的系数和次数的规律也是解决此类问题的关键.
10.【答案】
【解析】解:四边形是矩形,
,,
.
,
∽,
,
在中,,
,
解得.
故选:.
根据矩形的性质得,,即可得出,并根据勾股定理求出,再根据,得出∽,然后根据相似三角形对应边相等得出比例式,代入数值得出答案.
本题主要考查了矩形的性质,勾股定理,相似三角形的性质和判定,相似三角形的对应边成比例是求线段长的常用方法.
11.【答案】
【解析】解:扇形的弧长为:
,
圆锥的底面半径为:,
故选:.
易求得扇形的弧长,除以即为圆锥的底面半径.
考查了扇形的弧长公式,圆的周长公式,正确记忆圆锥的弧长等于底面周长是解题关键.
12.【答案】
【解析】解:解不等式,得:,
解不等式,得:,
不等式组的解集为,
,
解得,
故选:.
分别求出每一个不等式的解集,根据不等式组的解集,结合口诀:同大取大可得答案.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
13.【答案】
【解析】解:由题意得,
解得.
故答案为:.
根据被开方数大于等于列式计算即可得解.
本题考查了函数自变量的取值范围,解决本题的关键是二次根式的被开方数是非负数.
14.【答案】
【解析】 【解析】
分析原式提取公因式,再利用完全平方公式分解即可。
详解解:原式,
故答案为:
点评此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法,找出公因式是解本题的关键.
15.【答案】
【解析】解:反比例函数的图象位于第二、四象限,函数图象上一点到轴,轴的距离分别为和,
这个点的坐标为或,
,
故答案为:.
根据题意确定反比例函数图象上的这个点的坐标,再根据反比例函数图象上点的坐标特征进行计算即可.
本题考查反比例函数图象上点的坐标特征,确定这个点的坐标是正确解答的关键.
16.【答案】
【解析】解:设交于,连接,如图:
由作图可知:是线段的垂直平分线,
,
,
,
在中,
,
,
故答案为:.
设交于,连接,由作图可知:是线段的垂直平分线,即得,有,从而,由勾股定理得,故AB.
本题考查尺规作图中的计算问题,解题的关键是掌握用尺规作线段垂直平分线的方法,得到是线段的垂直平分线.
17.【答案】解:原式
.
【解析】先将二次根式化简、分别得出零指数幂、负整数指数幂、特殊角的三角函数值,然后根据实数的运算法则求得计算结果即可.
本题主要考查二次根式化简、零指数幂、负整数指数幂、特殊角的三角函数值,熟练掌握二次根式化简、零指数幂、负整数指数幂、特殊角的三角函数值的化简计算是解决本题的关键.
18.【答案】证明:,
,即.
在和中,
,
≌.
【解析】由与相等,利用等式的性质得到,利用得到三角形与三角形全等,利用全等三角形对应角相等即可得证.
此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.
19.【答案】
【解析】解:,
将七年级名同学比赛成绩重新排列为:,,,,,,,,,,
所以中位数,
八年级的成绩中分的最多,所以众数,
故答案为:,,;
七年级小杨同学在本年级排名更靠前,
理由:七年级的中位数为小于,说明小杨的成绩在本年级中是前名,
七年级小杨同学在本年级排名更靠前.
根据中位数和众数的概念求解即可;
根据中位数的意义即可得出答案.
本题考查频数分布表、中位数、众数、平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
20.【答案】
【解析】解:班、班共有名团员,其中男生有人,
因此从这两个班的全体团员中随机选取一名同学作为志愿者的组长,则这名同学是男生的概率为,
故答案为:;
用列表法表示所有可能出现的结果情况如下:
共有种能可能出现的结果数,其中一男一女的有种,
所以这两名同学恰好是一名男生、一名女生的概率为.
一共有名团员,其中男生有人,可求出抽取一人为男生的概率;
用列表法列举出从班、班各取一名团员所有可能出现的结果情况,进而求出相应的概率即可.
本题考查列表法或树状图法求随机事件的概率,列举出所有可能出现的结果情况是解决问题的关键.
21.【答案】证明:四边形是矩形
,,
,,
在和中
≌,
,
,
四边形是平行四边形,
,
平行四边形是菱形.
解:四边形是菱形,
,
设长为,则,
在中,
即,
解得:,
.
【解析】本题考查了矩形性质,平行四边形的判定,菱形的判定和性质,勾股定理等知识点的应用,对角线互相平分的四边形是平行四边形,对角线互相垂直的平行四边形是菱形.
根据矩形性质求出,推出,,证≌,推出,得出平行四边形,推出菱形;
根据菱形性质求出,在中,根据勾股定理得出,推出,再求面积即可.
22.【答案】解:设去年每吨土豆的平均价格是元,则今年第一次采购每吨土豆的平均价格为元,第二次采购每吨土豆的平均价格为元,
由题意得:,
解得:,
经检验,是原分式方程的解,且符合题意,
答:去年每吨土豆的平均价格是元;
由得:今年采购的土豆数为:吨,
设应将吨土豆加工成薯片,则应将吨加工成淀粉,
由题意得:,
解得:,
设总利润为元,
则,
,
随的增大而增大,
当时,的值最大,
答:为获得最大利润,应将吨土豆加工成薯片,最大利润是元.
【解析】设去年每吨土豆的平均价格是元,则第一次采购每吨土豆的平均价格为元,第二次采购每吨土豆的平均价格为元,根据第二次的采购数量是第一次采购数量的两倍,据此列出分式方程求解即可;
先求出今年采购的土豆数,根据采购的土豆需不超过天加工完毕,加工成薯片的土豆数量不少于加工成淀粉的土豆数量的,据此列出不等式组并求解,然后由一次函数的性质求出最大利润即可.
本题考查分式方程的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:找准数量关系,正确列出分式方程;找出数量关系,正确列出一元一次不等式组.
23.【答案】
【解析】证明:四边形是的内接四边形,
,
,
,
,
,
,
是的半径,
是圆的切线;
连接并延长交于点,连接,
是的直径,
,
,
,
在中,,
,
,
故答案为:.
根据圆内接四边形对角互补以及平角定义可得,然后根据已知可得,从而可得,即可解答;
连接并延长交于点,连接,根据直径所对的圆周角是直角可得,再利用同弧所对的圆周角相等可得,最后在中,利用锐角三角函数的定义进行计算即可解答.
本题考查了解直角三角形,切线的判定与性质,圆周角定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
24.【答案】
【解析】解:.
,
抛物线;
对称轴为.
故答案为:;
由知,,
;
把点,,代入得到,
,解得,
,
.
根据二次函数的对称轴公式求解即可;
首先利用待定系数法将,,代入得到,然后代入化简求值即可.
本题考查了二次函数的性质,二次函数图象与系数的关系,二次函数与坐标轴交点问题,掌握二次函数图象的性质是解题的关键.
第1页,共1页
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 实数的相反数是( )
A. B. C. D.
2. 如图是由个大小相同的正方体组成的几何体,该几何体的主视图是( )
A.
B.
C.
D.
3. 我国神舟十三号载人飞船和航天员乘组于年月日返回地球,结束了天的在轨飞行时间.从年神舟五号载人飞船上天以来,我国已有位航天员出征太空,绕地球飞行共约亿公里.将数据用科学记数法表示为( )
A. B. C. D.
4. 下列计算正确的是( )
A. B.
C. D.
5. 如图,已知,点在线段上不与点,点重合,连接若,,则( )
A.
B.
C.
D.
6. 一个多边形的内角和为,则这个多边形是( )
A. 七边形 B. 八边形 C. 九边形 D. 十边形
7. 每年月日为“世界读书日”,读书能丰富知识,陶冶情操,提高文化底蕴.某中学七年级一班统计了今年月“书香校园”读书活动中,全班同学的每月课外阅读数量单位:本及阅读不同种类书目数量,并绘制了如图所示的统计图,下列说法正确的是( )
A. 平均每月课外阅读数量大于本
B. 表示阅读“文学类”书籍的扇形圆心角是
C. 的值为
D. 根据调查统计结果发现“科幻类”书籍深受该中学七年级一班学生喜爱
8. 一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 有一个实数根 D. 没有实数根
9. 探索规律:观察下面的一列单项式:、、、、、,根据其中的规律得出的第个单项式是( )
A. B. C. D.
10. 如图,在矩形中,若,,,则的长为( )
A.
B.
C.
D.
11. 如图,如果从半径为的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥接缝处不重叠,则这个圆锥的底面半径为( )
A. B. C. D.
12. 若关于的不等式组,的解集为,则的取值范围是( )
A. B. C. D.
二、填空题(本大题共4小题,共8.0分)
13. 在函数中,自变量的取值范围是______.
14. 因式分解:______.
15. 反比例函数的图象位于第二、四象限,函数图象上一点到轴,轴的距离分别为和,则的值为______ .
16. 如图,在中,按以下步骤作图:分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;作直线交边于点若,,,则的长为______ .
三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
计算:.
18. 本小题分
如图,点,,,在一条直线上,,,求证:≌.
19. 本小题分
教育部发布的义务教育劳动课程标准年版,将劳动从原来的综合实践活动课程中完全独立出来,其中根据不同学段制定了“整理与收纳”“家庭清洁、烹饪、家居美化等日常生活劳动”等学段目标为了增强学生的劳动意识,让学生体验劳动的乐趣,某校组织七、八年级学生参加“美好双手,美好生活”劳动技能大赛,并随机抽取七年级和八年级各名同学的比赛成绩进行整理和分析,数据如下:
【收集数据】七年级名同学比赛成绩统计如下:,,,,,,,,,;
八年级名同学比赛成绩统计如下:,,,,,,,,,;
【整理数据】将两组数据按如下分数段整理,如表所示:
成绩
人数
年级
七年级
八年级
【分析数据】两组数据的平均数、中位数、众数、方差如表:
年级
统计量 平均数 中位数 众数 方差
七年级
八年级
【问题解决】根据以上信息,解答下列问题:
填空: ______ , ______ , ______ ;
样本数据中,七年级小杨同学和八年级小吴同学的成绩都为分,则哪位同学的成绩在本年级排名更靠前,请说明理由.
20. 本小题分
某校准备从八年级班、班的团员中选取两名同学作为运动会的志愿者,已知班有名团员其中男生人,女生人班有名团员其中男生人,女生人.
如果从这两个班的全体团员中随机选取一名同学作为志愿者的组长,则这名同学是男生的概率为______;
如果分别从班、班的团员中随机各选取一人,请用画树状图或列表的方法求这两名同学恰好是一名男生、一名女生的概率.
21. 本小题分
已知:如图,在矩形中,对角线的垂直平分线与相交于点,与相交于点,连接,.
求证:四边形是菱形;
若,,求菱形的面积.
22. 本小题分
今年我市某公司分两次采购了一批土豆,第一次花费万元,第二次花费万元,已知第一次采购时每吨土豆的价格比去年的平均价格上涨了元,第二次采购时每吨土豆的价格比去年的平均价格下降了元,第二次的采购数量是第一次采购数量的倍.
问去年每吨土豆的平均价格是多少元?
该公司可将土豆加工成薯片或淀粉,因设备原因,两种产品不能同时加工,若单独加工成薯片,每天可加工吨土豆,每吨土豆获利元;若单独加工成淀粉,每天可加工吨土豆,每吨土豆获利元,由于出口需要,所有采购的土豆必须全部加工完且用时不超过天,其中加工成薯片的土豆数量不少于加工成淀粉的土豆数量的,为获得最大利润,应将多少吨土豆加工成薯片?最大利润是多少?
23. 本小题分
如图,四边形内接于,是的直径,,的延长线交于点,延长交于点,.
求证:是的切线;
连接,,,的长为______.
24. 本小题分
已知抛物线,,,为常数且.
若,则抛物线的对称轴为直线______ ;
在的条件下,抛物线过点,,,求的值.
答案和解析
1.【答案】
【解析】解:实数的相反数是,
故选:.
根据相反数的定义直接求解.
本题主要考查相反数的定义,熟练掌握相反数的定义是解答此题的关键.
2.【答案】
【解析】
【分析】
主视图是从物体前面看所得到的图形,据此判断即可.
【解答】
解:根据主视图的概念,可知该几何体的主视图为:
故选:.
【点评】
本题考查三视图,掌握三视图的概念是解题的关键.
3.【答案】
【解析】解:.
故选:.
用科学记数法表示较大的数时,一般形式为,其中,为整数,且比原来的整数位数少,据此判断即可.
此题主要考查了用科学记数法表示较大的数,一般形式为,其中,确定与的值是解题的关键.
4.【答案】
【解析】
【分析】
根据同底数幂的除法法则,合并同类项法则,单项式乘单项式法则和完全平方公式对每个选项的结论作出判断即可得出结论.
【解答】
解:,选项的计算正确;
,选项的计算不正确;
,选项的计算不正确;
,选项的计算不正确.
故选:.
【点评】
本题主要考查了同底数幂的除法法则,合并同类项法则,单项式乘单项式法则和完全平方公式,正确使用上述法则与公式进行运算是解题的关键.
5.【答案】
【解析】解:为的外角,且,,
,即,
,
,
.
故选:.
由为的外角,利用外角性质求出的度数,再利用两直线平行内错角相等即可求出的度数.
此题考查了平行线的性质,以及外角性质,熟练掌握平行线的性质是解本题的关键.
6.【答案】
【解析】解:设多边形的边数为,
,
解得:.
故选:.
根据多边形的内角和公式:列出方程,解方程即可得出答案.
本题考查了多边形的内角和,体现了方程思想,掌握多边形的内角和是解题的关键.
7.【答案】
【解析】解:、七年级一班同学的平均每月课外阅读数量为本本,故错误,不符合题意;
B、表示阅读“文学类”书籍的扇形圆心角为,故错误,不符合题意;
C、,故,故错误,不符合题意;
D、“科幻类”书籍所占的比例最大,故“科幻类”书籍深受该中学七年级一班学生喜爱,正确,符合题意.
故选:.
A、求出平均每月课外阅读数量为本,可判断选项错误;
B、表示阅读“文学类”书籍的扇形圆心角为,可判断选项错误;
C、根据扇形统计表中所有项目所占比例之和为可求出值不是,可判断选项错误;
D、根据“科幻类”书籍所占的比例最大,可直接判断正确.
本题考查了条形统计图,扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
8.【答案】
【解析】解:,
所以方程有两个相等的实数根.
故选:.
计算出判别式的值即可得出答案.
本题主要考查根的判别式,一元二次方程的根与有如下关系:
当时,方程有两个不相等的两个实数根;
当时,方程有两个相等的两个实数根;
当时,方程无实数根.
9.【答案】
【解析】解:根据题意得:
第个单项式是.
故选:.
根据符号的规律:为奇数时,单项式为正号,为偶数时,符号为负号;系数的绝对值的规律:第个对应的系数的绝对值是指数的规律:第个对应的指数是解答即可.
本题考查了单项式的知识,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.分别找出单项式的系数和次数的规律也是解决此类问题的关键.
10.【答案】
【解析】解:四边形是矩形,
,,
.
,
∽,
,
在中,,
,
解得.
故选:.
根据矩形的性质得,,即可得出,并根据勾股定理求出,再根据,得出∽,然后根据相似三角形对应边相等得出比例式,代入数值得出答案.
本题主要考查了矩形的性质,勾股定理,相似三角形的性质和判定,相似三角形的对应边成比例是求线段长的常用方法.
11.【答案】
【解析】解:扇形的弧长为:
,
圆锥的底面半径为:,
故选:.
易求得扇形的弧长,除以即为圆锥的底面半径.
考查了扇形的弧长公式,圆的周长公式,正确记忆圆锥的弧长等于底面周长是解题关键.
12.【答案】
【解析】解:解不等式,得:,
解不等式,得:,
不等式组的解集为,
,
解得,
故选:.
分别求出每一个不等式的解集,根据不等式组的解集,结合口诀:同大取大可得答案.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
13.【答案】
【解析】解:由题意得,
解得.
故答案为:.
根据被开方数大于等于列式计算即可得解.
本题考查了函数自变量的取值范围,解决本题的关键是二次根式的被开方数是非负数.
14.【答案】
【解析】 【解析】
分析原式提取公因式,再利用完全平方公式分解即可。
详解解:原式,
故答案为:
点评此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法,找出公因式是解本题的关键.
15.【答案】
【解析】解:反比例函数的图象位于第二、四象限,函数图象上一点到轴,轴的距离分别为和,
这个点的坐标为或,
,
故答案为:.
根据题意确定反比例函数图象上的这个点的坐标,再根据反比例函数图象上点的坐标特征进行计算即可.
本题考查反比例函数图象上点的坐标特征,确定这个点的坐标是正确解答的关键.
16.【答案】
【解析】解:设交于,连接,如图:
由作图可知:是线段的垂直平分线,
,
,
,
在中,
,
,
故答案为:.
设交于,连接,由作图可知:是线段的垂直平分线,即得,有,从而,由勾股定理得,故AB.
本题考查尺规作图中的计算问题,解题的关键是掌握用尺规作线段垂直平分线的方法,得到是线段的垂直平分线.
17.【答案】解:原式
.
【解析】先将二次根式化简、分别得出零指数幂、负整数指数幂、特殊角的三角函数值,然后根据实数的运算法则求得计算结果即可.
本题主要考查二次根式化简、零指数幂、负整数指数幂、特殊角的三角函数值,熟练掌握二次根式化简、零指数幂、负整数指数幂、特殊角的三角函数值的化简计算是解决本题的关键.
18.【答案】证明:,
,即.
在和中,
,
≌.
【解析】由与相等,利用等式的性质得到,利用得到三角形与三角形全等,利用全等三角形对应角相等即可得证.
此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.
19.【答案】
【解析】解:,
将七年级名同学比赛成绩重新排列为:,,,,,,,,,,
所以中位数,
八年级的成绩中分的最多,所以众数,
故答案为:,,;
七年级小杨同学在本年级排名更靠前,
理由:七年级的中位数为小于,说明小杨的成绩在本年级中是前名,
七年级小杨同学在本年级排名更靠前.
根据中位数和众数的概念求解即可;
根据中位数的意义即可得出答案.
本题考查频数分布表、中位数、众数、平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
20.【答案】
【解析】解:班、班共有名团员,其中男生有人,
因此从这两个班的全体团员中随机选取一名同学作为志愿者的组长,则这名同学是男生的概率为,
故答案为:;
用列表法表示所有可能出现的结果情况如下:
共有种能可能出现的结果数,其中一男一女的有种,
所以这两名同学恰好是一名男生、一名女生的概率为.
一共有名团员,其中男生有人,可求出抽取一人为男生的概率;
用列表法列举出从班、班各取一名团员所有可能出现的结果情况,进而求出相应的概率即可.
本题考查列表法或树状图法求随机事件的概率,列举出所有可能出现的结果情况是解决问题的关键.
21.【答案】证明:四边形是矩形
,,
,,
在和中
≌,
,
,
四边形是平行四边形,
,
平行四边形是菱形.
解:四边形是菱形,
,
设长为,则,
在中,
即,
解得:,
.
【解析】本题考查了矩形性质,平行四边形的判定,菱形的判定和性质,勾股定理等知识点的应用,对角线互相平分的四边形是平行四边形,对角线互相垂直的平行四边形是菱形.
根据矩形性质求出,推出,,证≌,推出,得出平行四边形,推出菱形;
根据菱形性质求出,在中,根据勾股定理得出,推出,再求面积即可.
22.【答案】解:设去年每吨土豆的平均价格是元,则今年第一次采购每吨土豆的平均价格为元,第二次采购每吨土豆的平均价格为元,
由题意得:,
解得:,
经检验,是原分式方程的解,且符合题意,
答:去年每吨土豆的平均价格是元;
由得:今年采购的土豆数为:吨,
设应将吨土豆加工成薯片,则应将吨加工成淀粉,
由题意得:,
解得:,
设总利润为元,
则,
,
随的增大而增大,
当时,的值最大,
答:为获得最大利润,应将吨土豆加工成薯片,最大利润是元.
【解析】设去年每吨土豆的平均价格是元,则第一次采购每吨土豆的平均价格为元,第二次采购每吨土豆的平均价格为元,根据第二次的采购数量是第一次采购数量的两倍,据此列出分式方程求解即可;
先求出今年采购的土豆数,根据采购的土豆需不超过天加工完毕,加工成薯片的土豆数量不少于加工成淀粉的土豆数量的,据此列出不等式组并求解,然后由一次函数的性质求出最大利润即可.
本题考查分式方程的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:找准数量关系,正确列出分式方程;找出数量关系,正确列出一元一次不等式组.
23.【答案】
【解析】证明:四边形是的内接四边形,
,
,
,
,
,
,
是的半径,
是圆的切线;
连接并延长交于点,连接,
是的直径,
,
,
,
在中,,
,
,
故答案为:.
根据圆内接四边形对角互补以及平角定义可得,然后根据已知可得,从而可得,即可解答;
连接并延长交于点,连接,根据直径所对的圆周角是直角可得,再利用同弧所对的圆周角相等可得,最后在中,利用锐角三角函数的定义进行计算即可解答.
本题考查了解直角三角形,切线的判定与性质,圆周角定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
24.【答案】
【解析】解:.
,
抛物线;
对称轴为.
故答案为:;
由知,,
;
把点,,代入得到,
,解得,
,
.
根据二次函数的对称轴公式求解即可;
首先利用待定系数法将,,代入得到,然后代入化简求值即可.
本题考查了二次函数的性质,二次函数图象与系数的关系,二次函数与坐标轴交点问题,掌握二次函数图象的性质是解题的关键.
第1页,共1页
同课章节目录
