专题4 矩形的判定、判定与性质综合【七大题型分类归纳】重点题型全归纳2023-2024学年北师大版数学九年级上册(含解析)
文档属性
| 名称 | 专题4 矩形的判定、判定与性质综合【七大题型分类归纳】重点题型全归纳2023-2024学年北师大版数学九年级上册(含解析) | 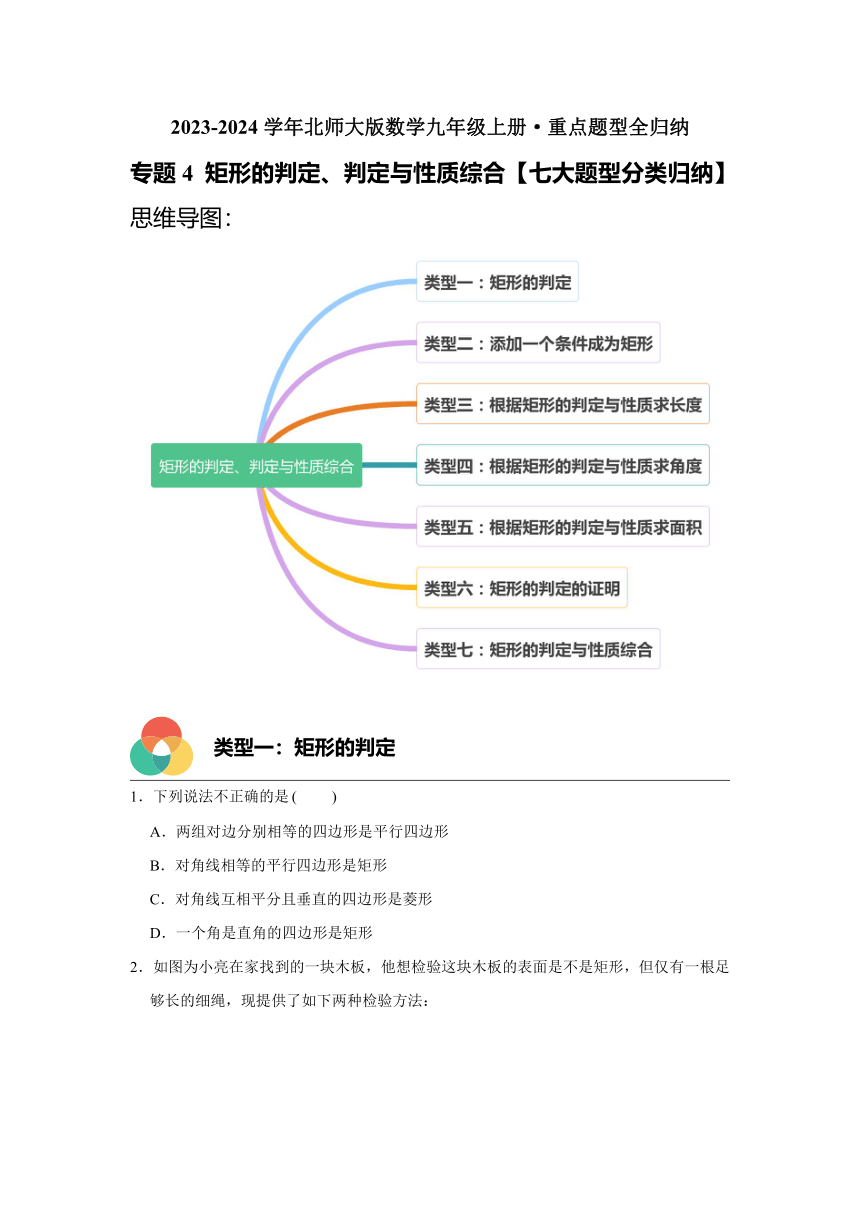 | |
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 20:45:31 | ||
图片预览




文档简介
2023-2024学年北师大版数学九年级上册·重点题型全归纳
专题4 矩形的判定、判定与性质综合【七大题型分类归纳】
思维导图:
类型一:矩形的判定
1.下列说法不正确的是
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
2.如图为小亮在家找到的一块木板,他想检验这块木板的表面是不是矩形,但仅有一根足够长的细绳,现提供了如下两种检验方法:
下列说法正确的是( )
A.方法一可行,方法二不可行
B.方法一不可行,方法二可行
C.方法一、二都可行
D.方法一、二都不可行
3.要检验一个四边形画框是否为矩形,可行的测量方法是
A.测量四边形画框的两个角是否为
B.测量四边形画框的对角线是否相等且互相平分
C.测量四边形画框的一组对边是否平行且相等
D.测量四边形画框的四边是否相等
4.如图,的对角线和相交于点,下列说法正确的是
A.若,则是菱形 B.若,则是矩形
C.若,则是菱形 D.若,则是矩形
5.下列条件中能判定一个平行四边形为矩形的是
①对角线互相平分
②对角线互相垂直
③对角线相等
④一组邻边相等
⑤一个角为直角
A.①④ B.②④ C.①② D.③⑤
类型二:添加一个条件成为矩形
6.在中,对角线,相交于点,若添加一个条件,使得为矩形,该条件是
A. B. C. D.
7.添加下列条件后,仍不能使它成为矩形的是
A. B. C. D.
8.在四边形中,,,请再添加一个条件,使四边形是矩形,添加的条件不能是
A. B. C. D.
9.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是
A. B. C. D.
10.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是
A. B. C. D.
类型三:根据矩形的判定与性质求长度
11.如图,在矩形中,点的坐标是,则的长是
A.3 B. C. D.4
12.如图,在中,对角线、相交于点,且,若,,则的长为
A. B. C.8 D.
13.如图,中,,,,是上一动点,过点作于点,于点,连接,则线段的最小值是
A.2.5 B.2.4 C.2.2 D.2
14.如图,点是菱形对角线的交点,,,连接,设,,则的长为
A.8 B.9 C.10 D.11
15.如图,在中,,,,为边上一动点不与,重合),于,于,为中点,则的取值范围是
A. B. C. D.
16.将一张矩形纸片(不是正方形),先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形,剩下的是如图所示的四边形纸片,其中,,,,则这张矩形纸片的较长边不可能是
A.6 B. C. D.8
类型四:根据矩形的判定与性质求角度
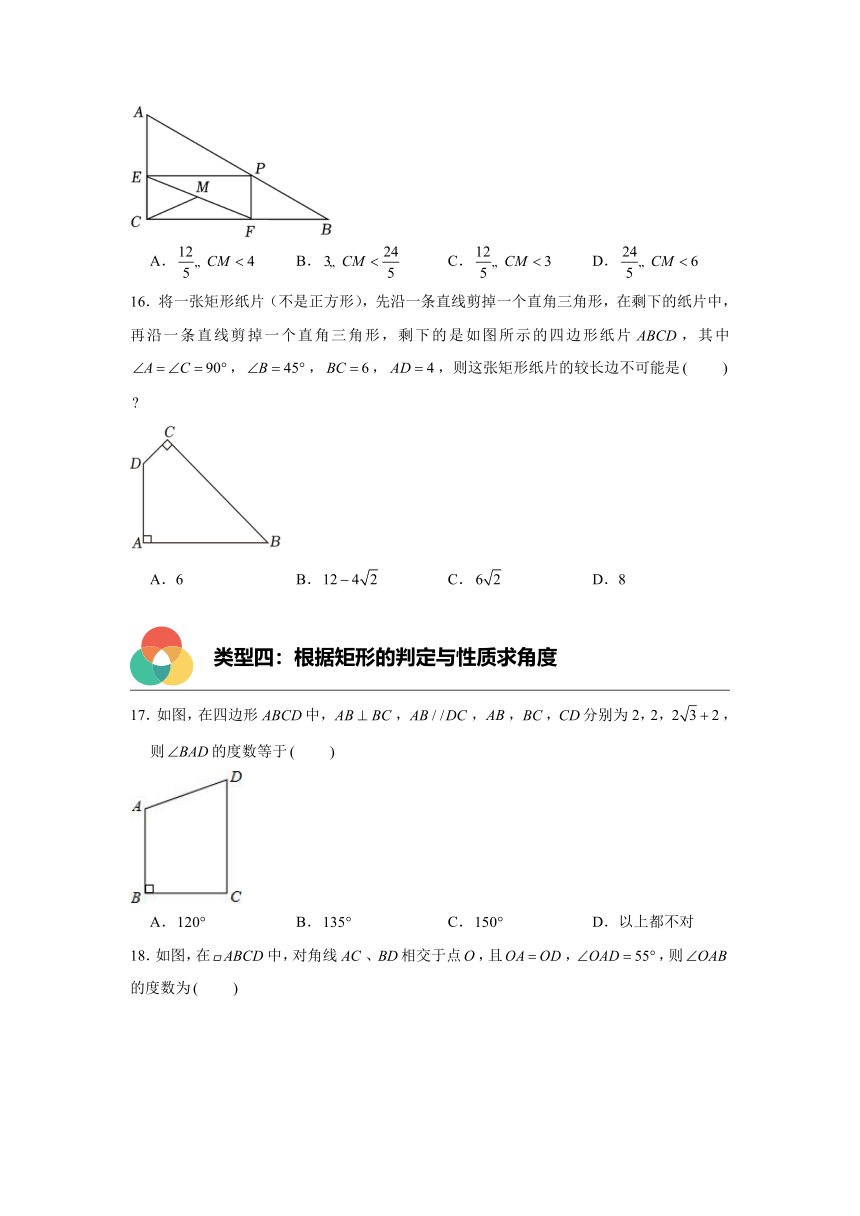
17.如图,在四边形中,,,,,分别为2,2,,则的度数等于
A. B. C. D.以上都不对
18.如图,在中,对角线、相交于点,且,,则的度数为
A. B. C. D.
19.如图,矩形在矩形的内部,且,点,在对角线的异侧.连结,,,,若矩形矩形,且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形的面积
A.矩形的面积 B.的度数
C.四边形的周长 D.的长度
20.如图,在平行四边形中,对角线、相交于点,且,,则的度数为
A. B. C. D.
类型五:根据矩形的判定与性质求面积
21.如图,中,的中垂线交、于点、,交延长线于点,若,,,则四边形的面积是
A. B. C. D.
22.如图,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.40 B.20 C.15 D.10
23.如图所示,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.6 B.8 C.12 D.24
24.如图,在矩形中,,,连接,以对角线为边,按逆时针方向作矩形,使矩形矩形;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,,按照此规律作下去.若矩形的面积记作,矩形的面积记作,矩形的面积记作,,则的值为
A. B. C. D.
类型六:矩形的判定的证明
25.如图,在中,于点,交于点.
求证:四边形是矩形.
26.如图,的对角线,相交于点,将对角线向两个方向延长,分别至点和点,且使.
(1)求证:四边形是平行四边形;
(2)若,求证:四边形是矩形.
27.如图,在中,,是的角平分线,点为的中点,延长交的外角平分线于点.
(1)求证:;
(2)连接,试判断四边形的形状,并证明你的结论.
28.如图,在中,延长至点,延长至点,且,.求证:是矩形.
29.如图,在中,,点、分别为、中点,连接并延长至点,使得,连接、、,求证:四边形为矩形.
30.如图,是的边的中点,连接、,且,求证:四边形是矩形.
类型七:矩形的判定与性质综合
31.如图,平行四边形中,对角线,相交于点,于点,于点,且.
(1)求证:四边形是矩形.
(2)若,求的度数.
32.如图,平行四边形中,点,分别在边,上,,,连接,.
(1)求证:四边形是矩形;
(2)若,,,求的长.
33.如图,平行四边形中,,过点作交的延长线于点,点为的中点,连接.
(1)求证:四边形是矩形;
(2)若,且,求四边形的面积.
34.如图,在中,,是边的中线,平分的外角,,垂足为.
(1)求证:四边形是矩形;
(2)连接,交于点,若,,则的面积是: .
35.如图,在平行四边形中,过点作交边于点,点在边上,且.
(1)求证:四边形是矩形.
(2)若平分,且,,求线段的长.
2023-2024学年北师大版数学九年级上册·重点题型全归纳
专题4 矩形的判定、判定与性质综合【七大题型分类归纳】
思维导图:
类型一:矩形的判定
1.下列说法不正确的是
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
【答案】
【分析】由菱形的判定和矩形的判定以及平行四边形的判定可求解.
【解答】解:、两组对边分别相等的四边形是平行四边形是正确的,故该选项不符合题意;
、对角线相等的平行四边形是矩形是正确的,故该选项不符合题意;
、对角线互相平分且垂直的四边形是菱形是正确的,故该选项不符合题意;
、一个角是直角的四边形是矩形是错误的,故该选项符合题意;
故选:.
【点评】本题考查了矩形的判定,平行四边形的判定和性质,菱形的判定,熟练运用这些判定是本题的关键.
2.如图为小亮在家找到的一块木板,他想检验这块木板的表面是不是矩形,但仅有一根足够长的细绳,现提供了如下两种检验方法:
下列说法正确的是( )
A.方法一可行,方法二不可行
B.方法一不可行,方法二可行
C.方法一、二都可行
D.方法一、二都不可行
【答案】A
【分析】根据矩形的判定进行判断即可.
【解答】解:方法一中:第一步得出四边形为平行四边形,
结合第二步得出:四边形为矩形;
方法二中不能直接得出是矩形,可能是等腰梯形,
故方法一可行,方法二不可行,
故选:A.
【点评】本题主要考查矩形的判定,熟练掌握矩形的判定定理是解题关键.
3.要检验一个四边形画框是否为矩形,可行的测量方法是
A.测量四边形画框的两个角是否为
B.测量四边形画框的对角线是否相等且互相平分
C.测量四边形画框的一组对边是否平行且相等
D.测量四边形画框的四边是否相等
【答案】
【分析】由平行四边形的判定与性质、菱形的判定,矩形的判定分别对各个选项进行判断即可.
【解答】解:、测量四边形画框的两个角是否为,不能判定为矩形,故选项不符合题意;
、测量四边形画框的对角线是否相等且互相平分,能判定为矩形,故选项符合题意;
、测量四边形画框的一组对边是否平行且相等,能判定为平行四边形,不能判定是否为矩形,故选项不符合题意;
、测量四边形画框的四边是否相等,能判定为菱形,故选项不符合题意;
故选:.
【点评】本题考查了矩形的判定、平行四边形的判定与性质等知识;熟记“对角线互相平分的四边形为平行四边形”是解题的关键.
4.如图,的对角线和相交于点,下列说法正确的是
A.若,则是菱形 B.若,则是矩形
C.若,则是菱形 D.若,则是矩形
【答案】
【分析】由矩形的判定和菱形的判定分别对各个选项进行判断即可.
【解答】解:、四边形是平行四边形,
,故选项不符合题意;
、四边形是平行四边形,,
是矩形,故选项符合题意;
、四边形是平行四边形,
,,
,
,
是矩形,故选项不符合题意;
、四边形是平行四边形,,
是菱形,故选项不符合题意;
故选:.
【点评】本题考查了菱形的判定、矩形的判定以及平行四边形的性质,熟练掌握菱形的判定和矩形的判定是解题的关键.
5.下列条件中能判定一个平行四边形为矩形的是
①对角线互相平分
②对角线互相垂直
③对角线相等
④一组邻边相等
⑤一个角为直角
A.①④ B.②④ C.①② D.③⑤
【答案】
【分析】根据平行四边形的判定(对角线互相平分),矩形的判定(对角线互相平分且相等),菱形的判定(对角线互相垂直的平行四边形)逐一判断即可.
【解答】解:①两条对角线互相平分的四边形是平行四边形;
②两条对角线互相垂直的平行四边形是菱形;
③对角线相等的平行四边形是矩形;
④一组邻边相等的平行四边形是菱形;
⑤一个角是直角的平行四边形是矩形.
能判定一个平行四边形为矩形的是③⑤,
故选:.
【点评】本题主要考查矩形的判定,平行四边形的判定,菱形的判定等知识点的理解和掌握,能熟练运用判定方法进行说理是解此题的关键.
类型二:添加一个条件成为矩形
6.在中,对角线,相交于点,若添加一个条件,使得为矩形,该条件是
A. B. C. D.
【答案】
【分析】由矩形的判定可直接求解.
【解答】解:四边形是平行四边形,,
四边形是矩形,
故选:.
【点评】本题考查了矩形的判定,平行四边形的性质,掌握矩形的判定是解题的关键.
7.添加下列条件后,仍不能使它成为矩形的是
A. B. C. D.
【答案】
【分析】根据矩形的判定和平行四边形的性质对各个选项进行判断即可.
【解答】解:、,
,
四边形是平行四边形,
是矩形,故选项不符合题意;
、四边形是平行四边形,,
是矩形,故选项不符合题意;
、四边形是平行四边形,
,
,
,
,
是矩形,故选项不符合题意;
、四边形是平行四边形,,
是菱形,故选项符合题意;
故选:.
【点评】本题考查了矩形的判定、平行四边形的性质以及菱形的判定;熟练掌握矩形的判定和平行四边形的性质是解题的关键.
8.在四边形中,,,请再添加一个条件,使四边形是矩形,添加的条件不能是
A. B. C. D.
【答案】
【分析】先证四边形是平行四边形,再由矩形的判定分别对各个选项进行判断即可.
【解答】解:,,
四边形是平行四边形,
、四边形是平行四边形,,
平行四边形是菱形,故选项符合题意;
、,
,
平行四边形是矩形,故选项不符合题意;
、四边形是平行四边形,,
平行四边形是矩形,故选项不符合题意;
、四边形是平行四边形,,
平行四边形是矩形,故选项不符合题意;
故选:.
【点评】本题考查了矩形的判定、平行四边形的判定与性质等知识,熟练掌握矩形的判定是解题的关键.
9.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是
A. B. C. D.
【答案】
【分析】先证四边形为平行四边形,再由矩形的判定和菱形的判定进行解答即可.
【解答】解:四边形为平行四边形,
,,
又,
,且,
四边形为平行四边形,
、,,
,
,
为矩形,故本选项不符合题意;
、对角线互相垂直的平行四边形为菱形,不一定为矩形,故本选项符合题意;
、,
,
为矩形,故本选项不符合题意;
、,
,
为矩形,故本选项不符合题意;
故选:.
【点评】本题考查了平行四边形的判定和性质、矩形的判定、菱形的判定等知识,熟练掌握矩形的判定是解题的关键.
10.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是
A. B. C. D.
【答案】
【分析】由平行四边形的判定与性质和矩形的判定即可得出结论.
【解答】解:添加时,四边形是矩形,理由如下:
,,
四边形是平行四边形,,
平行四边形是矩形,
故选:.
【点评】本题考查了矩形的判定以及平行四边形的判定与性质,熟练掌握矩形的判定是解题的关键.
类型三:根据矩形的判定与性质求长度
11.如图,在矩形中,点的坐标是,则的长是
A.3 B. C. D.4
【分析】根据勾股定理求得,然后根据矩形的性质得出.
【解答】解:四边形是矩形,
,
点的坐标是,
,
,
故选:.
【点评】本题考查了矩形的性质以及勾股定理的应用,熟练掌握矩形的性质是解题的关键.
12.如图,在中,对角线、相交于点,且,若,,则的长为
A. B. C.8 D.
【答案】
【分析】先证明,,于是可证明是矩形,为等边三角形,最后在中,依据特殊锐角三角函数值可求得的长.
【解答】解:四边形为平行四边形,
,,
,
,,
是矩形,
又,
为等边三角形.
.
.
.
故选:.
【点评】本题主要考查的是平行四边形的性质、等边三角形的判定、特殊锐角三角函数值的应用,求得是解题的关键.
13.如图,中,,,,是上一动点,过点作于点,于点,连接,则线段的最小值是
A.2.5 B.2.4 C.2.2 D.2
【分析】连接,利用勾股定理列式求出,判断出四边形是矩形,根据矩形的对角线相等可得,再根据垂线段最短可得时,线段的值最小,然后根据三角形的面积公式列出方程求解即可.
【解答】解:如图,连接.
,,,
,
,,,
四边形是矩形,
,
由垂线段最短可得时,线段的值最小,
此时,
即,
解得,
.
故选:.
【点评】本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出时,线段的值最小是解题的关键,难点在于利用三角形的面积列出方程.
14.如图,点是菱形对角线的交点,,,连接,设,,则的长为
A.8 B.9 C.10 D.11
【答案】
【分析】由菱形的性质和勾股定理求出,再证出平行四边形为矩形,得即可.
【解答】解:,,
四边形为平行四边形,
四边形是菱形,,,
,,,
,,
平行四边形为矩形,
,
故选:.
【点评】本题考查了菱形的性质,矩形的判定与性质,平行四边形判定与性质等知识;熟练掌握矩形的判定与性质是解题的关键.
15.如图,在中,,,,为边上一动点不与,重合),于,于,为中点,则的取值范围是
A. B. C. D.
【答案】
【分析】证明四边形是矩形,得,与互相平分,则,再求出的最小值可得的最小值,然后由,即可求得的取值范围.
【解答】解:如图,连接,
在中,,,,
,
于,于,
,
四边形是矩形,
,与互相平分,
为中点,
为的中点,
,
当时,,
此时有最小值为,
,
,
,
,
故选:.
【点评】此题考查了矩形的判定与性质、勾股定理、垂线段最短以及三角形面积等知识,熟练掌握矩形的判定与性质是解题的关键.
16.将一张矩形纸片(不是正方形),先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形,剩下的是如图所示的四边形纸片,其中,,,,则这张矩形纸片的较长边不可能是
A.6 B. C. D.8
【答案】
【分析】分四种情况画出图形,求出最长的直角边即可.
【解答】解:延长,,过点作,交的延长线于点,过点作交的延长线于点,如图所示:
,
,
,,
四边形为平行四边形,
,
四边形为矩形,
,,
.,
,
,
为等腰直角三角形,
,
,
,
,
,
此时较长的边为;
延长,过点作,过点作交延长线于点,交的垂线于点,
如图所示:
,
,
,
四边形为平行四边形,
,
四边形为矩形,
,
,
为等腰直角三角形,
,
,
,
为等腰直角三角形,
,
,
此时较长的边为6;
延长,,过点作,交的延长线于点,过点作,交的延长线于点,
如图所示:
,,
,
,
四边形为平行四边形,
,
四边形为矩形,
,,
.
为等腰三角形,
,
,
,,
为等腰直角三角形,
,
,
此时较长的边为,
综上分析可知,矩形纸片(不是正方形)时,较长的边为或或6或,
不可能为8,
正确,
故选:.
【点评】本题主要考查了矩形的判定和性质,等腰直角三角形的性质,平行线的判定,解题的关键是分情况画出图形,数形结合.
类型四:根据矩形的判定与性质求角度
17.如图,在四边形中,,,,,分别为2,2,,则的度数等于
A. B. C. D.以上都不对
【分析】过作于,得出四边形是矩形,根据矩形的性质求出,,,根据勾股定理求出,即可求出的度数,求出答案即可.
【解答】解:过作于,
,,
,
四边形是矩形,
,,,
,
,
由勾股定理得:,
,,
,
,
故选:.
【点评】本题考查了矩形的性质和判定,含角的直角三角形性质,勾股定理的应用,能构造直角三角形并求出的度数是解此题的关键.
18.如图,在中,对角线、相交于点,且,,则的度数为
A. B. C. D.
【分析】根据矩形的判定得到四边形是矩形,由矩形的性质求出,代入求出即可.
【解答】解:四边形是平行四边形,
,,
,
,
四边形是矩形,
,
,
故选:.
【点评】本题考查了矩形的判定和性质,能根据矩形的性质求出的度数是解此题的关键.
19.如图,矩形在矩形的内部,且,点,在对角线的异侧.连结,,,,若矩形矩形,且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形的面积
A.矩形的面积 B.的度数
C.四边形的周长 D.的长度
【答案】
【分析】连接,,过点作于点,过点作于点,过点作于点,过点作于点,设小矩形的长和宽分别为和,大矩形的长和宽分别为和,,,然后用分割法求得四边形的面积,进而可以根据条件得到结果.
【解答】解:如图,连接,,过点作于点,过点作于点,过点作于点,过点作于点,
,
四边形、四边形是矩形,
设小矩形的长和宽分别为和,大矩形的长和宽分别为和,,,则,,,,
,,,,
,
矩形和矩形的周长已知,
和为定值,
为定值,
为定值,
,
当已知时,四边形的面积即为定值,
故选:.
【点评】本题考查了矩形的判定与性质,解题的关键是学会设矩形的长和宽并用含有未知数的式子表示矩形、矩形和四边形的面积.
20.如图,在平行四边形中,对角线、相交于点,且,,则的度数为
A. B. C. D.
【答案】
【分析】根据矩形的判定得到四边形是矩形,由矩形的性质求出,,求出,由平行线的性质即可得出答案.
【解答】解:四边形是平行四边形,
,,
,
,
四边形是矩形,
,,
,,
故选:.
【点评】本题考查了矩形的判定和性质、平行四边形的性质等知识,熟练掌握矩形的判定与性质是解此题的关键.
类型五:根据矩形的判定与性质求面积
21.如图,中,的中垂线交、于点、,交延长线于点,若,,,则四边形的面积是
A. B. C. D.
【分析】先证明是等边三角形,得出,,求出,再证明四边形是矩形,即可求出面积.
【解答】解:连接,如图所示:
是的中垂线,
,,
,
,
,
,
是等边三角形,
,,
,,
,
,
四边形是矩形,
四边形的面积;
故选:.
【点评】本题考查了矩形的判定与性质、线段垂直平分线的性质、三角函数以及等边三角形的判定与性质;证明等边三角形和矩形是解决问题的关键.
22.如图,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.40 B.20 C.15 D.10
【答案】
【分析】根据图形的拼剪,可得,根据三角形中位线定理求出,根据矩形的面积公式即可解决问题.
【解答】解:由题意,,
点、是、的中点,
是的中位线,
,
,
矩形的面积.
故选:.
【点评】本题主要考查了矩形的面积公式,三角形中位线定理,熟记三角形的中位线等于第三边的一半是解决问题的关键.
23.如图所示,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.6 B.8 C.12 D.24
【答案】
【分析】根据题意,得,,,由三角形中位线定理求出,即可求出矩形的面积.
【解答】解:根据题意,得,,,
是的中位线,
,
.
故选:.
【点评】本题主要考查了三角形中位线定理,矩形的面积公式,正确理解题意,根据三角形中位线定理求出是解决问题的关键.
24.如图,在矩形中,,,连接,以对角线为边,按逆时针方向作矩形,使矩形矩形;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,,按照此规律作下去.若矩形的面积记作,矩形的面积记作,矩形的面积记作,,则的值为
A. B. C. D.
【答案】
【分析】根据已知和矩形的性质可分别求得,再利用相似多边形的性质可发现规律,然后根据规律即可求解.
【解答】解:四边形是矩形,
,
,
按逆时针方向作矩形的相似矩形,
矩形的边长和矩形的边长的比为
矩形的面积和矩形的面积的比,
,,,
,,
故选:.
【点评】本题考查了矩形的性质,勾股定理,相似多边形的性质,解此题的关键是能根据求出的结果得出规律.
类型六:矩形的判定的证明
25.如图,在中,于点,交于点.
求证:四边形是矩形.
【答案】见解析.
【分析】根据平行四边形的性质得到,根据平行四边形的判定得到四边形是平行四边形,根据矩形的判定定理即可得到结论.
【解答】证明:在中,,
,
,,
,,
四边形是平行四边形,
,
是矩形.
【点评】本题考查了矩形的判定,平行四边形的判定和性质,熟练掌握矩形的判定是解题的关键.
26.如图,的对角线,相交于点,将对角线向两个方向延长,分别至点和点,且使.
(1)求证:四边形是平行四边形;
(2)若,求证:四边形是矩形.
【答案】证明见解析.
【分析】(1)由四边形是平行四边形易知,,再证得,即可得出结论;
(2)由平行四边形的性质证出,根据矩形的判定可得出结论.
【解答】证明:(1)四边形是平行四边形,
,,
又,
.
四边形是平行四边形.
(2)四边形是平行四边形,
,,
,
,
四边形是平行四边形,
四边形是矩形.
【点评】此题考查了平行四边形的性质和判定,熟练掌握平行四边形的判定与性质是解题的关键,解题时要注意选择适宜的判定方法.
27.如图,在中,,是的角平分线,点为的中点,延长交的外角平分线于点.
(1)求证:;
(2)连接,试判断四边形的形状,并证明你的结论.
【答案】(1)见解析过程;
(2)四边形是矩形,理由见解析过程.
【分析】(1)由等腰三角形的性质可得,,由三角形的中位线定理可得,由直角三角形的性质和平行线的性质可证;
(2)由矩形的判定可得结论.
【解答】(1)证明:,是的角平分线,
,,
点是的中点,
是的中位线,,
,
,
平分,
,
,
,
;
(2)解:四边形是矩形,理由如下:
如图,
,,
四边形是平行四边形,
,
四边形是矩形.
【点评】本题考查了矩形的判定,等腰三角形的性质,三角形中位线定理等知识,灵活运用这些性质解决问题是解题的关键.
28.如图,在中,延长至点,延长至点,且,.求证:是矩形.
【答案】见解析.
【分析】根据平行四边形的性质得到,,根据平行线的性质得到,根据全等三角形的性质得到,根据矩形的判定定理即可得到结论.
【解答】证明:四边形是平行四边形,
,,
,
,
,
在与中,
,
,
,
,
是矩形.
【点评】本题考查了矩形的判定,平行四边形的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.
29.如图,在中,,点、分别为、中点,连接并延长至点,使得,连接、、,求证:四边形为矩形.
【答案】证明见解析.
【分析】根据平行四边形的判定得出四边形是平行四边形,再根据等腰三角形的性质和矩形的判定解答即可.
【解答】证明:点、分别为、中点,
,,
,
四边形是平行四边形,
,,
,
,
是矩形.
【点评】此题考查矩形的判定,关键是根据平行四边形的判定得出四边形是平行四边形解答.
30.如图,是的边的中点,连接、,且,求证:四边形是矩形.
【答案】证明见解答.
【分析】由平行四边形的性质得,而,,即可根据全等三角形的判定定理“”证明,得,因为,所以,即可证明四边形是矩形.
【解答】证明:四边形是平行四边形,
,,
是的中点,
,
在和中,
,
,
,
,
,
四边形是矩形.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质、矩形的判定等知识,证明是解题的关键.
类型七:矩形的判定与性质综合
31.如图,平行四边形中,对角线,相交于点,于点,于点,且.
(1)求证:四边形是矩形.
(2)若,求的度数.
【答案】(1)见解析;(2).
【分析】(1)证,得出,则,即可得出四边形是矩形.
(2)由矩形的性质得出,,则,求出,则,即可得出答案.
【解答】(1)证明:四边形是平行四边形,
,,
于点,于点,
,
在和中,
,
,
,
,
四边形是矩形.
(2)解:由(1)得:四边形是矩形,
,,
,
于点,
,
,
,
,
.
.
【点评】本题考查了矩形的判定与性质、平行四边形的性质、全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握矩形的判定与性质,证明三角形全等是解题的关键.
32.如图,平行四边形中,点,分别在边,上,,,连接,.
(1)求证:四边形是矩形;
(2)若,,,求的长.
【答案】(1)证明见解析;
(2).
【分析】(1)先证四边形是平行四边形,再由矩形的判定即可得出结论;
(2)由平行四边形的性质得,,,再由矩形的性质得,进而由含角的直角三角形的性质得,然后由勾股定理得,即可解决问题.
【解答】(1)证明:四边形是平行四边形,
,,
,
,
,
即,
四边形是平行四边形,
又,
四边形是矩形;
(2)解:四边形是平行四边形,
,,,
由(1)可知,四边形是矩形,
,
,
,
,
,
,
.
【点评】本题考查了平行四边形的判定与性质、矩形的判定与性质、含角的直角三角形的性质以及勾股定理等知识,熟练掌握矩形的判定与性质是解题的关键.
33.如图,平行四边形中,,过点作交的延长线于点,点为的中点,连接.
(1)求证:四边形是矩形;
(2)若,且,求四边形的面积.
【答案】(1)证明见解析过程;
(2)90.
【分析】(1)利用平行线的性质分析可得,从而求证四边形是矩形;
(2)根据直角三角形斜边中线等于斜边的一半和勾股定理求得的长度,从而利用矩形和三角形的面积公式计算求解.
【解答】(1)证明:平行四边形中,,
,
,
,
,
,
四边形是矩形;
(2)解:,点为的中点,,
,
在中,,
平行四边形中,,
在矩形中,,
四边形的面积
.
【点评】本题考查平行四边形的性质,矩形的判定,理解直角三角形斜边中线等于斜边的一半,掌握平行四边形的性质及矩形的判定方法是解题关键.
34.如图,在中,,是边的中线,平分的外角,,垂足为.
(1)求证:四边形是矩形;
(2)连接,交于点,若,,则的面积是: 12 .
【答案】(1)证明过程请看解答;
(2)12.
【分析】(1)证出四边形有三个直角即可;
(2)由矩形的性质得,由勾股定理求出,再由三角形面积公式即可得答案.
【解答】(1)证明:在中,,是边的中线,
,,
,
为的外角的平分线,
,
,
,
,
四边形为矩形;
(2)解:是边的中线,,
,
由(1)得:四边形是矩形,
,
在中,,
的面积;
故答案为:12.
【点评】此题考查了矩形的判定与性质、等腰三角形的性质、勾股定理等知识;熟练掌握矩形的判定与性质是解题的关键.
35.如图,在平行四边形中,过点作交边于点,点在边上,且.
(1)求证:四边形是矩形.
(2)若平分,且,,求线段的长.
【分析】(1)首先证明,,推出四边形是平行四边形,再证明即可解决问题;
(2)分别在,中,利用勾股定理求出、即可;
【解答】(1)证明:四边形是平行四边形,
,,
,
,
四边形是平行四边形,
,
,
四边形是矩形.
(2)解:平分,,
,
,,
在中,,
在中,.
【点评】本题考查平行四边形的性质、矩形的判定和性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
专题4 矩形的判定、判定与性质综合【七大题型分类归纳】
思维导图:
类型一:矩形的判定
1.下列说法不正确的是
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
2.如图为小亮在家找到的一块木板,他想检验这块木板的表面是不是矩形,但仅有一根足够长的细绳,现提供了如下两种检验方法:
下列说法正确的是( )
A.方法一可行,方法二不可行
B.方法一不可行,方法二可行
C.方法一、二都可行
D.方法一、二都不可行
3.要检验一个四边形画框是否为矩形,可行的测量方法是
A.测量四边形画框的两个角是否为
B.测量四边形画框的对角线是否相等且互相平分
C.测量四边形画框的一组对边是否平行且相等
D.测量四边形画框的四边是否相等
4.如图,的对角线和相交于点,下列说法正确的是
A.若,则是菱形 B.若,则是矩形
C.若,则是菱形 D.若,则是矩形
5.下列条件中能判定一个平行四边形为矩形的是
①对角线互相平分
②对角线互相垂直
③对角线相等
④一组邻边相等
⑤一个角为直角
A.①④ B.②④ C.①② D.③⑤
类型二:添加一个条件成为矩形
6.在中,对角线,相交于点,若添加一个条件,使得为矩形,该条件是
A. B. C. D.
7.添加下列条件后,仍不能使它成为矩形的是
A. B. C. D.
8.在四边形中,,,请再添加一个条件,使四边形是矩形,添加的条件不能是
A. B. C. D.
9.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是
A. B. C. D.
10.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是
A. B. C. D.
类型三:根据矩形的判定与性质求长度
11.如图,在矩形中,点的坐标是,则的长是
A.3 B. C. D.4
12.如图,在中,对角线、相交于点,且,若,,则的长为
A. B. C.8 D.
13.如图,中,,,,是上一动点,过点作于点,于点,连接,则线段的最小值是
A.2.5 B.2.4 C.2.2 D.2
14.如图,点是菱形对角线的交点,,,连接,设,,则的长为
A.8 B.9 C.10 D.11
15.如图,在中,,,,为边上一动点不与,重合),于,于,为中点,则的取值范围是
A. B. C. D.
16.将一张矩形纸片(不是正方形),先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形,剩下的是如图所示的四边形纸片,其中,,,,则这张矩形纸片的较长边不可能是
A.6 B. C. D.8
类型四:根据矩形的判定与性质求角度
17.如图,在四边形中,,,,,分别为2,2,,则的度数等于
A. B. C. D.以上都不对
18.如图,在中,对角线、相交于点,且,,则的度数为
A. B. C. D.
19.如图,矩形在矩形的内部,且,点,在对角线的异侧.连结,,,,若矩形矩形,且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形的面积
A.矩形的面积 B.的度数
C.四边形的周长 D.的长度
20.如图,在平行四边形中,对角线、相交于点,且,,则的度数为
A. B. C. D.
类型五:根据矩形的判定与性质求面积
21.如图,中,的中垂线交、于点、,交延长线于点,若,,,则四边形的面积是
A. B. C. D.
22.如图,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.40 B.20 C.15 D.10
23.如图所示,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.6 B.8 C.12 D.24
24.如图,在矩形中,,,连接,以对角线为边,按逆时针方向作矩形,使矩形矩形;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,,按照此规律作下去.若矩形的面积记作,矩形的面积记作,矩形的面积记作,,则的值为
A. B. C. D.
类型六:矩形的判定的证明
25.如图,在中,于点,交于点.
求证:四边形是矩形.
26.如图,的对角线,相交于点,将对角线向两个方向延长,分别至点和点,且使.
(1)求证:四边形是平行四边形;
(2)若,求证:四边形是矩形.
27.如图,在中,,是的角平分线,点为的中点,延长交的外角平分线于点.
(1)求证:;
(2)连接,试判断四边形的形状,并证明你的结论.
28.如图,在中,延长至点,延长至点,且,.求证:是矩形.
29.如图,在中,,点、分别为、中点,连接并延长至点,使得,连接、、,求证:四边形为矩形.
30.如图,是的边的中点,连接、,且,求证:四边形是矩形.
类型七:矩形的判定与性质综合
31.如图,平行四边形中,对角线,相交于点,于点,于点,且.
(1)求证:四边形是矩形.
(2)若,求的度数.
32.如图,平行四边形中,点,分别在边,上,,,连接,.
(1)求证:四边形是矩形;
(2)若,,,求的长.
33.如图,平行四边形中,,过点作交的延长线于点,点为的中点,连接.
(1)求证:四边形是矩形;
(2)若,且,求四边形的面积.
34.如图,在中,,是边的中线,平分的外角,,垂足为.
(1)求证:四边形是矩形;
(2)连接,交于点,若,,则的面积是: .
35.如图,在平行四边形中,过点作交边于点,点在边上,且.
(1)求证:四边形是矩形.
(2)若平分,且,,求线段的长.
2023-2024学年北师大版数学九年级上册·重点题型全归纳
专题4 矩形的判定、判定与性质综合【七大题型分类归纳】
思维导图:
类型一:矩形的判定
1.下列说法不正确的是
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
【答案】
【分析】由菱形的判定和矩形的判定以及平行四边形的判定可求解.
【解答】解:、两组对边分别相等的四边形是平行四边形是正确的,故该选项不符合题意;
、对角线相等的平行四边形是矩形是正确的,故该选项不符合题意;
、对角线互相平分且垂直的四边形是菱形是正确的,故该选项不符合题意;
、一个角是直角的四边形是矩形是错误的,故该选项符合题意;
故选:.
【点评】本题考查了矩形的判定,平行四边形的判定和性质,菱形的判定,熟练运用这些判定是本题的关键.
2.如图为小亮在家找到的一块木板,他想检验这块木板的表面是不是矩形,但仅有一根足够长的细绳,现提供了如下两种检验方法:
下列说法正确的是( )
A.方法一可行,方法二不可行
B.方法一不可行,方法二可行
C.方法一、二都可行
D.方法一、二都不可行
【答案】A
【分析】根据矩形的判定进行判断即可.
【解答】解:方法一中:第一步得出四边形为平行四边形,
结合第二步得出:四边形为矩形;
方法二中不能直接得出是矩形,可能是等腰梯形,
故方法一可行,方法二不可行,
故选:A.
【点评】本题主要考查矩形的判定,熟练掌握矩形的判定定理是解题关键.
3.要检验一个四边形画框是否为矩形,可行的测量方法是
A.测量四边形画框的两个角是否为
B.测量四边形画框的对角线是否相等且互相平分
C.测量四边形画框的一组对边是否平行且相等
D.测量四边形画框的四边是否相等
【答案】
【分析】由平行四边形的判定与性质、菱形的判定,矩形的判定分别对各个选项进行判断即可.
【解答】解:、测量四边形画框的两个角是否为,不能判定为矩形,故选项不符合题意;
、测量四边形画框的对角线是否相等且互相平分,能判定为矩形,故选项符合题意;
、测量四边形画框的一组对边是否平行且相等,能判定为平行四边形,不能判定是否为矩形,故选项不符合题意;
、测量四边形画框的四边是否相等,能判定为菱形,故选项不符合题意;
故选:.
【点评】本题考查了矩形的判定、平行四边形的判定与性质等知识;熟记“对角线互相平分的四边形为平行四边形”是解题的关键.
4.如图,的对角线和相交于点,下列说法正确的是
A.若,则是菱形 B.若,则是矩形
C.若,则是菱形 D.若,则是矩形
【答案】
【分析】由矩形的判定和菱形的判定分别对各个选项进行判断即可.
【解答】解:、四边形是平行四边形,
,故选项不符合题意;
、四边形是平行四边形,,
是矩形,故选项符合题意;
、四边形是平行四边形,
,,
,
,
是矩形,故选项不符合题意;
、四边形是平行四边形,,
是菱形,故选项不符合题意;
故选:.
【点评】本题考查了菱形的判定、矩形的判定以及平行四边形的性质,熟练掌握菱形的判定和矩形的判定是解题的关键.
5.下列条件中能判定一个平行四边形为矩形的是
①对角线互相平分
②对角线互相垂直
③对角线相等
④一组邻边相等
⑤一个角为直角
A.①④ B.②④ C.①② D.③⑤
【答案】
【分析】根据平行四边形的判定(对角线互相平分),矩形的判定(对角线互相平分且相等),菱形的判定(对角线互相垂直的平行四边形)逐一判断即可.
【解答】解:①两条对角线互相平分的四边形是平行四边形;
②两条对角线互相垂直的平行四边形是菱形;
③对角线相等的平行四边形是矩形;
④一组邻边相等的平行四边形是菱形;
⑤一个角是直角的平行四边形是矩形.
能判定一个平行四边形为矩形的是③⑤,
故选:.
【点评】本题主要考查矩形的判定,平行四边形的判定,菱形的判定等知识点的理解和掌握,能熟练运用判定方法进行说理是解此题的关键.
类型二:添加一个条件成为矩形
6.在中,对角线,相交于点,若添加一个条件,使得为矩形,该条件是
A. B. C. D.
【答案】
【分析】由矩形的判定可直接求解.
【解答】解:四边形是平行四边形,,
四边形是矩形,
故选:.
【点评】本题考查了矩形的判定,平行四边形的性质,掌握矩形的判定是解题的关键.
7.添加下列条件后,仍不能使它成为矩形的是
A. B. C. D.
【答案】
【分析】根据矩形的判定和平行四边形的性质对各个选项进行判断即可.
【解答】解:、,
,
四边形是平行四边形,
是矩形,故选项不符合题意;
、四边形是平行四边形,,
是矩形,故选项不符合题意;
、四边形是平行四边形,
,
,
,
,
是矩形,故选项不符合题意;
、四边形是平行四边形,,
是菱形,故选项符合题意;
故选:.
【点评】本题考查了矩形的判定、平行四边形的性质以及菱形的判定;熟练掌握矩形的判定和平行四边形的性质是解题的关键.
8.在四边形中,,,请再添加一个条件,使四边形是矩形,添加的条件不能是
A. B. C. D.
【答案】
【分析】先证四边形是平行四边形,再由矩形的判定分别对各个选项进行判断即可.
【解答】解:,,
四边形是平行四边形,
、四边形是平行四边形,,
平行四边形是菱形,故选项符合题意;
、,
,
平行四边形是矩形,故选项不符合题意;
、四边形是平行四边形,,
平行四边形是矩形,故选项不符合题意;
、四边形是平行四边形,,
平行四边形是矩形,故选项不符合题意;
故选:.
【点评】本题考查了矩形的判定、平行四边形的判定与性质等知识,熟练掌握矩形的判定是解题的关键.
9.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是
A. B. C. D.
【答案】
【分析】先证四边形为平行四边形,再由矩形的判定和菱形的判定进行解答即可.
【解答】解:四边形为平行四边形,
,,
又,
,且,
四边形为平行四边形,
、,,
,
,
为矩形,故本选项不符合题意;
、对角线互相垂直的平行四边形为菱形,不一定为矩形,故本选项符合题意;
、,
,
为矩形,故本选项不符合题意;
、,
,
为矩形,故本选项不符合题意;
故选:.
【点评】本题考查了平行四边形的判定和性质、矩形的判定、菱形的判定等知识,熟练掌握矩形的判定是解题的关键.
10.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是
A. B. C. D.
【答案】
【分析】由平行四边形的判定与性质和矩形的判定即可得出结论.
【解答】解:添加时,四边形是矩形,理由如下:
,,
四边形是平行四边形,,
平行四边形是矩形,
故选:.
【点评】本题考查了矩形的判定以及平行四边形的判定与性质,熟练掌握矩形的判定是解题的关键.
类型三:根据矩形的判定与性质求长度
11.如图,在矩形中,点的坐标是,则的长是
A.3 B. C. D.4
【分析】根据勾股定理求得,然后根据矩形的性质得出.
【解答】解:四边形是矩形,
,
点的坐标是,
,
,
故选:.
【点评】本题考查了矩形的性质以及勾股定理的应用,熟练掌握矩形的性质是解题的关键.
12.如图,在中,对角线、相交于点,且,若,,则的长为
A. B. C.8 D.
【答案】
【分析】先证明,,于是可证明是矩形,为等边三角形,最后在中,依据特殊锐角三角函数值可求得的长.
【解答】解:四边形为平行四边形,
,,
,
,,
是矩形,
又,
为等边三角形.
.
.
.
故选:.
【点评】本题主要考查的是平行四边形的性质、等边三角形的判定、特殊锐角三角函数值的应用,求得是解题的关键.
13.如图,中,,,,是上一动点,过点作于点,于点,连接,则线段的最小值是
A.2.5 B.2.4 C.2.2 D.2
【分析】连接,利用勾股定理列式求出,判断出四边形是矩形,根据矩形的对角线相等可得,再根据垂线段最短可得时,线段的值最小,然后根据三角形的面积公式列出方程求解即可.
【解答】解:如图,连接.
,,,
,
,,,
四边形是矩形,
,
由垂线段最短可得时,线段的值最小,
此时,
即,
解得,
.
故选:.
【点评】本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出时,线段的值最小是解题的关键,难点在于利用三角形的面积列出方程.
14.如图,点是菱形对角线的交点,,,连接,设,,则的长为
A.8 B.9 C.10 D.11
【答案】
【分析】由菱形的性质和勾股定理求出,再证出平行四边形为矩形,得即可.
【解答】解:,,
四边形为平行四边形,
四边形是菱形,,,
,,,
,,
平行四边形为矩形,
,
故选:.
【点评】本题考查了菱形的性质,矩形的判定与性质,平行四边形判定与性质等知识;熟练掌握矩形的判定与性质是解题的关键.
15.如图,在中,,,,为边上一动点不与,重合),于,于,为中点,则的取值范围是
A. B. C. D.
【答案】
【分析】证明四边形是矩形,得,与互相平分,则,再求出的最小值可得的最小值,然后由,即可求得的取值范围.
【解答】解:如图,连接,
在中,,,,
,
于,于,
,
四边形是矩形,
,与互相平分,
为中点,
为的中点,
,
当时,,
此时有最小值为,
,
,
,
,
故选:.
【点评】此题考查了矩形的判定与性质、勾股定理、垂线段最短以及三角形面积等知识,熟练掌握矩形的判定与性质是解题的关键.
16.将一张矩形纸片(不是正方形),先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形,剩下的是如图所示的四边形纸片,其中,,,,则这张矩形纸片的较长边不可能是
A.6 B. C. D.8
【答案】
【分析】分四种情况画出图形,求出最长的直角边即可.
【解答】解:延长,,过点作,交的延长线于点,过点作交的延长线于点,如图所示:
,
,
,,
四边形为平行四边形,
,
四边形为矩形,
,,
.,
,
,
为等腰直角三角形,
,
,
,
,
,
此时较长的边为;
延长,过点作,过点作交延长线于点,交的垂线于点,
如图所示:
,
,
,
四边形为平行四边形,
,
四边形为矩形,
,
,
为等腰直角三角形,
,
,
,
为等腰直角三角形,
,
,
此时较长的边为6;
延长,,过点作,交的延长线于点,过点作,交的延长线于点,
如图所示:
,,
,
,
四边形为平行四边形,
,
四边形为矩形,
,,
.
为等腰三角形,
,
,
,,
为等腰直角三角形,
,
,
此时较长的边为,
综上分析可知,矩形纸片(不是正方形)时,较长的边为或或6或,
不可能为8,
正确,
故选:.
【点评】本题主要考查了矩形的判定和性质,等腰直角三角形的性质,平行线的判定,解题的关键是分情况画出图形,数形结合.
类型四:根据矩形的判定与性质求角度
17.如图,在四边形中,,,,,分别为2,2,,则的度数等于
A. B. C. D.以上都不对
【分析】过作于,得出四边形是矩形,根据矩形的性质求出,,,根据勾股定理求出,即可求出的度数,求出答案即可.
【解答】解:过作于,
,,
,
四边形是矩形,
,,,
,
,
由勾股定理得:,
,,
,
,
故选:.
【点评】本题考查了矩形的性质和判定,含角的直角三角形性质,勾股定理的应用,能构造直角三角形并求出的度数是解此题的关键.
18.如图,在中,对角线、相交于点,且,,则的度数为
A. B. C. D.
【分析】根据矩形的判定得到四边形是矩形,由矩形的性质求出,代入求出即可.
【解答】解:四边形是平行四边形,
,,
,
,
四边形是矩形,
,
,
故选:.
【点评】本题考查了矩形的判定和性质,能根据矩形的性质求出的度数是解此题的关键.
19.如图,矩形在矩形的内部,且,点,在对角线的异侧.连结,,,,若矩形矩形,且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形的面积
A.矩形的面积 B.的度数
C.四边形的周长 D.的长度
【答案】
【分析】连接,,过点作于点,过点作于点,过点作于点,过点作于点,设小矩形的长和宽分别为和,大矩形的长和宽分别为和,,,然后用分割法求得四边形的面积,进而可以根据条件得到结果.
【解答】解:如图,连接,,过点作于点,过点作于点,过点作于点,过点作于点,
,
四边形、四边形是矩形,
设小矩形的长和宽分别为和,大矩形的长和宽分别为和,,,则,,,,
,,,,
,
矩形和矩形的周长已知,
和为定值,
为定值,
为定值,
,
当已知时,四边形的面积即为定值,
故选:.
【点评】本题考查了矩形的判定与性质,解题的关键是学会设矩形的长和宽并用含有未知数的式子表示矩形、矩形和四边形的面积.
20.如图,在平行四边形中,对角线、相交于点,且,,则的度数为
A. B. C. D.
【答案】
【分析】根据矩形的判定得到四边形是矩形,由矩形的性质求出,,求出,由平行线的性质即可得出答案.
【解答】解:四边形是平行四边形,
,,
,
,
四边形是矩形,
,,
,,
故选:.
【点评】本题考查了矩形的判定和性质、平行四边形的性质等知识,熟练掌握矩形的判定与性质是解此题的关键.
类型五:根据矩形的判定与性质求面积
21.如图,中,的中垂线交、于点、,交延长线于点,若,,,则四边形的面积是
A. B. C. D.
【分析】先证明是等边三角形,得出,,求出,再证明四边形是矩形,即可求出面积.
【解答】解:连接,如图所示:
是的中垂线,
,,
,
,
,
,
是等边三角形,
,,
,,
,
,
四边形是矩形,
四边形的面积;
故选:.
【点评】本题考查了矩形的判定与性质、线段垂直平分线的性质、三角函数以及等边三角形的判定与性质;证明等边三角形和矩形是解决问题的关键.
22.如图,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.40 B.20 C.15 D.10
【答案】
【分析】根据图形的拼剪,可得,根据三角形中位线定理求出,根据矩形的面积公式即可解决问题.
【解答】解:由题意,,
点、是、的中点,
是的中位线,
,
,
矩形的面积.
故选:.
【点评】本题主要考查了矩形的面积公式,三角形中位线定理,熟记三角形的中位线等于第三边的一半是解决问题的关键.
23.如图所示,在中,分别取、的中点、,连接,过点作,垂足为,将分割后拼接成矩形.若,,则矩形的面积是
A.6 B.8 C.12 D.24
【答案】
【分析】根据题意,得,,,由三角形中位线定理求出,即可求出矩形的面积.
【解答】解:根据题意,得,,,
是的中位线,
,
.
故选:.
【点评】本题主要考查了三角形中位线定理,矩形的面积公式,正确理解题意,根据三角形中位线定理求出是解决问题的关键.
24.如图,在矩形中,,,连接,以对角线为边,按逆时针方向作矩形,使矩形矩形;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,,按照此规律作下去.若矩形的面积记作,矩形的面积记作,矩形的面积记作,,则的值为
A. B. C. D.
【答案】
【分析】根据已知和矩形的性质可分别求得,再利用相似多边形的性质可发现规律,然后根据规律即可求解.
【解答】解:四边形是矩形,
,
,
按逆时针方向作矩形的相似矩形,
矩形的边长和矩形的边长的比为
矩形的面积和矩形的面积的比,
,,,
,,
故选:.
【点评】本题考查了矩形的性质,勾股定理,相似多边形的性质,解此题的关键是能根据求出的结果得出规律.
类型六:矩形的判定的证明
25.如图,在中,于点,交于点.
求证:四边形是矩形.
【答案】见解析.
【分析】根据平行四边形的性质得到,根据平行四边形的判定得到四边形是平行四边形,根据矩形的判定定理即可得到结论.
【解答】证明:在中,,
,
,,
,,
四边形是平行四边形,
,
是矩形.
【点评】本题考查了矩形的判定,平行四边形的判定和性质,熟练掌握矩形的判定是解题的关键.
26.如图,的对角线,相交于点,将对角线向两个方向延长,分别至点和点,且使.
(1)求证:四边形是平行四边形;
(2)若,求证:四边形是矩形.
【答案】证明见解析.
【分析】(1)由四边形是平行四边形易知,,再证得,即可得出结论;
(2)由平行四边形的性质证出,根据矩形的判定可得出结论.
【解答】证明:(1)四边形是平行四边形,
,,
又,
.
四边形是平行四边形.
(2)四边形是平行四边形,
,,
,
,
四边形是平行四边形,
四边形是矩形.
【点评】此题考查了平行四边形的性质和判定,熟练掌握平行四边形的判定与性质是解题的关键,解题时要注意选择适宜的判定方法.
27.如图,在中,,是的角平分线,点为的中点,延长交的外角平分线于点.
(1)求证:;
(2)连接,试判断四边形的形状,并证明你的结论.
【答案】(1)见解析过程;
(2)四边形是矩形,理由见解析过程.
【分析】(1)由等腰三角形的性质可得,,由三角形的中位线定理可得,由直角三角形的性质和平行线的性质可证;
(2)由矩形的判定可得结论.
【解答】(1)证明:,是的角平分线,
,,
点是的中点,
是的中位线,,
,
,
平分,
,
,
,
;
(2)解:四边形是矩形,理由如下:
如图,
,,
四边形是平行四边形,
,
四边形是矩形.
【点评】本题考查了矩形的判定,等腰三角形的性质,三角形中位线定理等知识,灵活运用这些性质解决问题是解题的关键.
28.如图,在中,延长至点,延长至点,且,.求证:是矩形.
【答案】见解析.
【分析】根据平行四边形的性质得到,,根据平行线的性质得到,根据全等三角形的性质得到,根据矩形的判定定理即可得到结论.
【解答】证明:四边形是平行四边形,
,,
,
,
,
在与中,
,
,
,
,
是矩形.
【点评】本题考查了矩形的判定,平行四边形的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.
29.如图,在中,,点、分别为、中点,连接并延长至点,使得,连接、、,求证:四边形为矩形.
【答案】证明见解析.
【分析】根据平行四边形的判定得出四边形是平行四边形,再根据等腰三角形的性质和矩形的判定解答即可.
【解答】证明:点、分别为、中点,
,,
,
四边形是平行四边形,
,,
,
,
是矩形.
【点评】此题考查矩形的判定,关键是根据平行四边形的判定得出四边形是平行四边形解答.
30.如图,是的边的中点,连接、,且,求证:四边形是矩形.
【答案】证明见解答.
【分析】由平行四边形的性质得,而,,即可根据全等三角形的判定定理“”证明,得,因为,所以,即可证明四边形是矩形.
【解答】证明:四边形是平行四边形,
,,
是的中点,
,
在和中,
,
,
,
,
,
四边形是矩形.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质、矩形的判定等知识,证明是解题的关键.
类型七:矩形的判定与性质综合
31.如图,平行四边形中,对角线,相交于点,于点,于点,且.
(1)求证:四边形是矩形.
(2)若,求的度数.
【答案】(1)见解析;(2).
【分析】(1)证,得出,则,即可得出四边形是矩形.
(2)由矩形的性质得出,,则,求出,则,即可得出答案.
【解答】(1)证明:四边形是平行四边形,
,,
于点,于点,
,
在和中,
,
,
,
,
四边形是矩形.
(2)解:由(1)得:四边形是矩形,
,,
,
于点,
,
,
,
,
.
.
【点评】本题考查了矩形的判定与性质、平行四边形的性质、全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握矩形的判定与性质,证明三角形全等是解题的关键.
32.如图,平行四边形中,点,分别在边,上,,,连接,.
(1)求证:四边形是矩形;
(2)若,,,求的长.
【答案】(1)证明见解析;
(2).
【分析】(1)先证四边形是平行四边形,再由矩形的判定即可得出结论;
(2)由平行四边形的性质得,,,再由矩形的性质得,进而由含角的直角三角形的性质得,然后由勾股定理得,即可解决问题.
【解答】(1)证明:四边形是平行四边形,
,,
,
,
,
即,
四边形是平行四边形,
又,
四边形是矩形;
(2)解:四边形是平行四边形,
,,,
由(1)可知,四边形是矩形,
,
,
,
,
,
,
.
【点评】本题考查了平行四边形的判定与性质、矩形的判定与性质、含角的直角三角形的性质以及勾股定理等知识,熟练掌握矩形的判定与性质是解题的关键.
33.如图,平行四边形中,,过点作交的延长线于点,点为的中点,连接.
(1)求证:四边形是矩形;
(2)若,且,求四边形的面积.
【答案】(1)证明见解析过程;
(2)90.
【分析】(1)利用平行线的性质分析可得,从而求证四边形是矩形;
(2)根据直角三角形斜边中线等于斜边的一半和勾股定理求得的长度,从而利用矩形和三角形的面积公式计算求解.
【解答】(1)证明:平行四边形中,,
,
,
,
,
,
四边形是矩形;
(2)解:,点为的中点,,
,
在中,,
平行四边形中,,
在矩形中,,
四边形的面积
.
【点评】本题考查平行四边形的性质,矩形的判定,理解直角三角形斜边中线等于斜边的一半,掌握平行四边形的性质及矩形的判定方法是解题关键.
34.如图,在中,,是边的中线,平分的外角,,垂足为.
(1)求证:四边形是矩形;
(2)连接,交于点,若,,则的面积是: 12 .
【答案】(1)证明过程请看解答;
(2)12.
【分析】(1)证出四边形有三个直角即可;
(2)由矩形的性质得,由勾股定理求出,再由三角形面积公式即可得答案.
【解答】(1)证明:在中,,是边的中线,
,,
,
为的外角的平分线,
,
,
,
,
四边形为矩形;
(2)解:是边的中线,,
,
由(1)得:四边形是矩形,
,
在中,,
的面积;
故答案为:12.
【点评】此题考查了矩形的判定与性质、等腰三角形的性质、勾股定理等知识;熟练掌握矩形的判定与性质是解题的关键.
35.如图,在平行四边形中,过点作交边于点,点在边上,且.
(1)求证:四边形是矩形.
(2)若平分,且,,求线段的长.
【分析】(1)首先证明,,推出四边形是平行四边形,再证明即可解决问题;
(2)分别在,中,利用勾股定理求出、即可;
【解答】(1)证明:四边形是平行四边形,
,,
,
,
四边形是平行四边形,
,
,
四边形是矩形.
(2)解:平分,,
,
,,
在中,,
在中,.
【点评】本题考查平行四边形的性质、矩形的判定和性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
