1.1 正数和负数 同步练测 知识清单+练基础+练能力+练素养 (含解析)
文档属性
| 名称 | 1.1 正数和负数 同步练测 知识清单+练基础+练能力+练素养 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 74.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学七年级上册1.1正数和负数
【知识清单】
1、负数:比 小的数。负数与正数表示意义相反的量。负数用 号,即相当于减号 “-”标记,如 2,代表的就是2的相反数。
2、正数:比 大的数。正数与负数表示意义相反的量。正数前面常有一个符号“+”,通常可以省略不写
注意:
1、 既不是正数,也不是负数。
2、字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
3、正数有时也可以在前面加“+”,有时“+”省略不写。所以省略“+”的正数的符号是正号。
【练基础】
【知识点1】正数和负数的概念
1.在-2,3.2,-14,0,,中,负数有( )
A.1个 B.2个 C.3个 D.4个
9.已知下列各数:-7, 3.6, , 0, -2.5, 10, -1,其中非负数有( )
A.2个 B.3个 C.4个 D.5个
【知识点2】用正负数表示具有相反意义的量
2. 如果60m表示“向北走60m”,那么“向南走40m”可以表示为( )
A.-20m B.-40m C.20m D.40m
3.如果+3吨表示运入仓库的大米吨数,那么运出5吨大米表示为:( )
A.-5吨 B.+5吨 C.-3吨 D.+3吨
4.下列不是具有相反意义的量是( )
A.前进5米和后退5米
B.节约3吨和消费10吨
C.身高增加2厘米和体重减少2千克
D.超过5克和不足2克
5.若火箭发射点火前5秒记作-5秒,则火箭发射点火后10秒应记作 .
6.某单位开展了职工健步走活动,职工每天健步走5000步即为达标.若小夏走了6200步,记为+1200步,小辰走了4800步,记为 步.
7.在树上有一只蜗牛,白天向上挪动7cm,记为,晚间向下掉了,可记作 cm.
8.有8筐白菜,以每筐25kg为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下: , ,2, ,1, , , ,这8筐白菜一共多少千克?
【练能力】
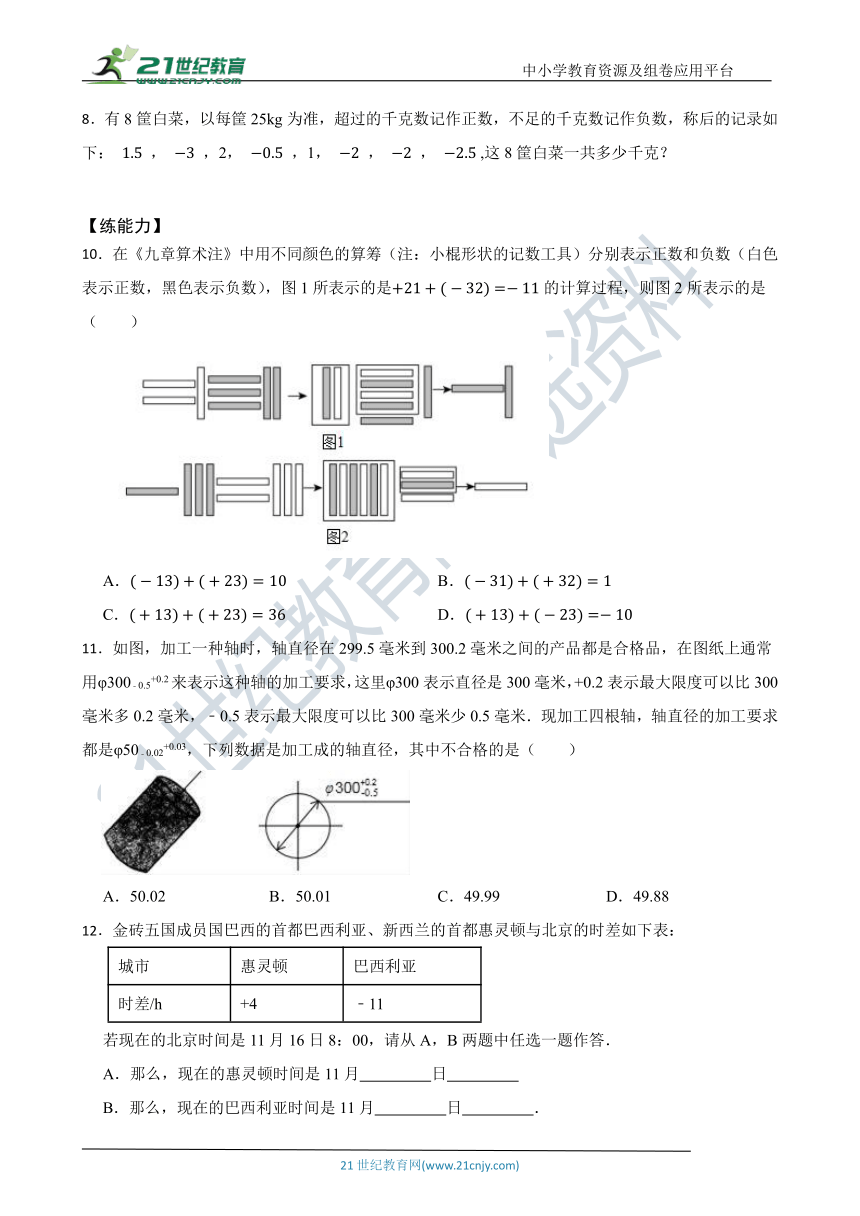
10.在《九章算术注》中用不同颜色的算筹(注:小棍形状的记数工具)分别表示正数和负数(白色表示正数,黑色表示负数),图1所表示的是的计算过程,则图2所表示的是( )
A. B.
C. D.
11.如图,加工一种轴时,轴直径在299.5毫米到300.2毫米之间的产品都是合格品,在图纸上通常用φ300﹣0.5+0.2来表示这种轴的加工要求,这里φ300表示直径是300毫米,+0.2表示最大限度可以比300毫米多0.2毫米,﹣0.5表示最大限度可以比300毫米少0.5毫米.现加工四根轴,轴直径的加工要求都是φ50﹣0.02+0.03,下列数据是加工成的轴直径,其中不合格的是( )
A.50.02 B.50.01 C.49.99 D.49.88
12.金砖五国成员国巴西的首都巴西利亚、新西兰的首都惠灵顿与北京的时差如下表:
城市 惠灵顿 巴西利亚
时差/h +4 ﹣11
若现在的北京时间是11月16日8:00,请从A,B两题中任选一题作答.
A.那么,现在的惠灵顿时间是11月 日
B.那么,现在的巴西利亚时间是11月 日 .
13.一组按规律排列的数: , , , , , ,其中第 个数是 ,第 ( 为正整数)个数是 .
14.某粮店出售的两种品牌的面粉袋上分别标有质量为(25±0.1)kg,(25±0.2)kg的字样,从中任意拿出两袋,它们的质量最多相差 kg.
【素养提升】
15.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1,﹣2);
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
(4)若图中另有两个格点M、N,且M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),则N→A应记为什么?
答案解析部分
【知识清单】
1、0;负
2、0
注意:0
【练基础】
1.【答案】C
【知识点】正数和负数的认识及应用
【解析】【解答】解:该题目中是负数的有,,,共3个.
故答案为:C.
【分析】负数是小于0的数,据此判断.
2.【答案】C
【知识点】正数和负数的认识及应用
【解析】【解答】解:下列各数:-7, 3.6, , 0, -2.5, 10, -1,是非负数有3.6, , 0, 10,一共有4个.
故答案为:C
【分析】利用正数和0统称为非负数,可得到已知数中非负数的个数.
3.【答案】B
【知识点】正数和负数的认识及应用
【解析】【分析】本题需先根据已知条件得出正数表示向北走,从而得出向南走需用负数表示,最后即可得出答案.
【解答】60m表示“向北走60m”,
那么“向南走40m”可以表示-40米.
故选B.
4.【答案】A
【知识点】正数和负数的认识及应用
【解析】【解答】运入为正,运出为负,则运出5吨大米为-5吨.
故A符合题意.
故答案为:A.
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
5.【答案】C
【知识点】正数和负数的认识及应用
【解析】【解答】C选项中的身高和体重不是同一个单位量,所以这两个量的变化不具有相反的意义.
【分析】注意相反意义的量应该是表示的同一个单位量.
6.【答案】+10秒
【知识点】正数和负数的认识及应用
【解析】【解答】解:若火箭发射点火前5秒记为-5秒,则点火后为正;那么火箭发射点火后10秒应记为+10秒.
故答案为:+10秒.
【分析】根据正数与负数可以表示具有相反意义的一对量,故弄清楚了负数所表示的量,即可得出答案.
7.【答案】
【知识点】正数和负数的认识及应用
【解析】【解答】解:∵5000步达标地,6200步记为步,
∴(步),低于5000步记为负,
∴4800步记为步,
故答案为:.
【分析】由题意可知:高于5000步记为正,低于5000步记为负,用5000-4800,结合题意即可求解.
8.【答案】-3
【知识点】正数和负数的认识及应用
【解析】【解答】解:∵正”和“负”相对,
∴若白天向上挪动,记作,那么晚间向下掉了,可记作.
故答案为:-3.
【分析】由于正数与负数可以表示一对具有相反意义的量,故弄清楚了正数所表示的量,即可得出答案.
9.【答案】 解:依题可得:
1.5+(-3)+2+(-0.5)+1+(-2)+(-2)+(-2.5),
=1.5-3+2-0.5+1-2-2-2.5,
=-5.5(千克),
∴25×8-5.5=194.5(千克).
答:这8筐白菜一共194.5千克.
【知识点】正数和负数的认识及应用
【解析】【分析】根据题意列出算式,计算即可得出答案.
【练能力】
10.【答案】A
【知识点】正数和负数的认识及应用
【解析】【解答】解:由图1可知,一横表示10,一竖表示1,白色为正,黑色为负,
则图2表示的过程是计算,
故答案为:A.
【分析】根据图1的计算方法可得图2表示的过程是计算。
11.【答案】D
【知识点】正数和负数的认识及应用
【解析】【解答】由题意得:合格范围为:50﹣0.02=49.98到50+0.03=50.03,
而49.88mm<49.98mm,
故可得D不合格,
故答案为:D.
【分析】根据题意计算得到合格的范围,根据零件的加工的直径,判断其是否在合格范围之内即可得到答案。
12.【答案】16;12;15;21
【知识点】正数和负数的认识及应用
【解析】【解答】A.8+4=12,所以现在的惠灵顿时间是11月16日12时;
B.8﹣11=﹣3,24﹣3=21,所以现在的巴西利亚时间是11月15日21时,
故答案为:16,12;15,21.
【分析】根据北京时间,结合时差将时间作和或者作差得到答案即可。
13.【答案】;
【知识点】正数和负数的认识及应用
【解析】【解答】解:观察数字规律,是一负,一正,一负,一正,所以用 表示符合;
再观察分母是 , , , , 是奇数,所以用 表示奇数;
最后观察分子是 , , , , ,后一个是前一个的 倍,用 表示第 个,
所以第 个数是 ,第 个数是 .
故答案为: , .
【分析】根据数的规律,得到答案即可。
14.【答案】0.4
【知识点】正数和负数的认识及应用
【解析】【解答】解:依题可得,
面粉最重的为25+0.2kg,面粉最轻的为25-0.2kg,
∴质量最多相差:0.2-(-0.2)=0.4(kg),
故答案为:0.4.
【分析】根据题中给出面粉的波动范围,求出其中两袋相差最大的数.
【素养提升】
15.【答案】(1)+3;+4;+2;0;D
(2)解:P点位置如图1所示;
(3)解:如图2,
根据已知条件可知:
A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);
则该甲虫走过的路线长为:1+4+2+1+2=10
(4)解:由M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),
所以,5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,
所以,点A向右走2个格点,向上走2个格点到点N,
所以,N→A应记为(﹣2,﹣2)
【知识点】正数和负数的认识及应用
【解析】【解答】解:(1)图中A→C(+3,+4),B→C(+2,0),C→D(+1,﹣2);
故答案为:(+3,+4),(+2,0),D;
【分析】(1)根据向上向右走均为正,向下向左走均为负确定数据即可;
(2)根据所给的路线确定点的位置即可;
(3)根据表示的路线确定长度相加可得结果;
(4)观察点的变化情况,根据(1)即可确定点走了格数,从而确定结论.
21世纪教育网(www.21cnjy.com)
初中数学七年级上册1.1正数和负数
【知识清单】
1、负数:比 小的数。负数与正数表示意义相反的量。负数用 号,即相当于减号 “-”标记,如 2,代表的就是2的相反数。
2、正数:比 大的数。正数与负数表示意义相反的量。正数前面常有一个符号“+”,通常可以省略不写
注意:
1、 既不是正数,也不是负数。
2、字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
3、正数有时也可以在前面加“+”,有时“+”省略不写。所以省略“+”的正数的符号是正号。
【练基础】
【知识点1】正数和负数的概念
1.在-2,3.2,-14,0,,中,负数有( )
A.1个 B.2个 C.3个 D.4个
9.已知下列各数:-7, 3.6, , 0, -2.5, 10, -1,其中非负数有( )
A.2个 B.3个 C.4个 D.5个
【知识点2】用正负数表示具有相反意义的量
2. 如果60m表示“向北走60m”,那么“向南走40m”可以表示为( )
A.-20m B.-40m C.20m D.40m
3.如果+3吨表示运入仓库的大米吨数,那么运出5吨大米表示为:( )
A.-5吨 B.+5吨 C.-3吨 D.+3吨
4.下列不是具有相反意义的量是( )
A.前进5米和后退5米
B.节约3吨和消费10吨
C.身高增加2厘米和体重减少2千克
D.超过5克和不足2克
5.若火箭发射点火前5秒记作-5秒,则火箭发射点火后10秒应记作 .
6.某单位开展了职工健步走活动,职工每天健步走5000步即为达标.若小夏走了6200步,记为+1200步,小辰走了4800步,记为 步.
7.在树上有一只蜗牛,白天向上挪动7cm,记为,晚间向下掉了,可记作 cm.
8.有8筐白菜,以每筐25kg为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下: , ,2, ,1, , , ,这8筐白菜一共多少千克?
【练能力】
10.在《九章算术注》中用不同颜色的算筹(注:小棍形状的记数工具)分别表示正数和负数(白色表示正数,黑色表示负数),图1所表示的是的计算过程,则图2所表示的是( )
A. B.
C. D.
11.如图,加工一种轴时,轴直径在299.5毫米到300.2毫米之间的产品都是合格品,在图纸上通常用φ300﹣0.5+0.2来表示这种轴的加工要求,这里φ300表示直径是300毫米,+0.2表示最大限度可以比300毫米多0.2毫米,﹣0.5表示最大限度可以比300毫米少0.5毫米.现加工四根轴,轴直径的加工要求都是φ50﹣0.02+0.03,下列数据是加工成的轴直径,其中不合格的是( )
A.50.02 B.50.01 C.49.99 D.49.88
12.金砖五国成员国巴西的首都巴西利亚、新西兰的首都惠灵顿与北京的时差如下表:
城市 惠灵顿 巴西利亚
时差/h +4 ﹣11
若现在的北京时间是11月16日8:00,请从A,B两题中任选一题作答.
A.那么,现在的惠灵顿时间是11月 日
B.那么,现在的巴西利亚时间是11月 日 .
13.一组按规律排列的数: , , , , , ,其中第 个数是 ,第 ( 为正整数)个数是 .
14.某粮店出售的两种品牌的面粉袋上分别标有质量为(25±0.1)kg,(25±0.2)kg的字样,从中任意拿出两袋,它们的质量最多相差 kg.
【素养提升】
15.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1,﹣2);
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
(4)若图中另有两个格点M、N,且M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),则N→A应记为什么?
答案解析部分
【知识清单】
1、0;负
2、0
注意:0
【练基础】
1.【答案】C
【知识点】正数和负数的认识及应用
【解析】【解答】解:该题目中是负数的有,,,共3个.
故答案为:C.
【分析】负数是小于0的数,据此判断.
2.【答案】C
【知识点】正数和负数的认识及应用
【解析】【解答】解:下列各数:-7, 3.6, , 0, -2.5, 10, -1,是非负数有3.6, , 0, 10,一共有4个.
故答案为:C
【分析】利用正数和0统称为非负数,可得到已知数中非负数的个数.
3.【答案】B
【知识点】正数和负数的认识及应用
【解析】【分析】本题需先根据已知条件得出正数表示向北走,从而得出向南走需用负数表示,最后即可得出答案.
【解答】60m表示“向北走60m”,
那么“向南走40m”可以表示-40米.
故选B.
4.【答案】A
【知识点】正数和负数的认识及应用
【解析】【解答】运入为正,运出为负,则运出5吨大米为-5吨.
故A符合题意.
故答案为:A.
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
5.【答案】C
【知识点】正数和负数的认识及应用
【解析】【解答】C选项中的身高和体重不是同一个单位量,所以这两个量的变化不具有相反的意义.
【分析】注意相反意义的量应该是表示的同一个单位量.
6.【答案】+10秒
【知识点】正数和负数的认识及应用
【解析】【解答】解:若火箭发射点火前5秒记为-5秒,则点火后为正;那么火箭发射点火后10秒应记为+10秒.
故答案为:+10秒.
【分析】根据正数与负数可以表示具有相反意义的一对量,故弄清楚了负数所表示的量,即可得出答案.
7.【答案】
【知识点】正数和负数的认识及应用
【解析】【解答】解:∵5000步达标地,6200步记为步,
∴(步),低于5000步记为负,
∴4800步记为步,
故答案为:.
【分析】由题意可知:高于5000步记为正,低于5000步记为负,用5000-4800,结合题意即可求解.
8.【答案】-3
【知识点】正数和负数的认识及应用
【解析】【解答】解:∵正”和“负”相对,
∴若白天向上挪动,记作,那么晚间向下掉了,可记作.
故答案为:-3.
【分析】由于正数与负数可以表示一对具有相反意义的量,故弄清楚了正数所表示的量,即可得出答案.
9.【答案】 解:依题可得:
1.5+(-3)+2+(-0.5)+1+(-2)+(-2)+(-2.5),
=1.5-3+2-0.5+1-2-2-2.5,
=-5.5(千克),
∴25×8-5.5=194.5(千克).
答:这8筐白菜一共194.5千克.
【知识点】正数和负数的认识及应用
【解析】【分析】根据题意列出算式,计算即可得出答案.
【练能力】
10.【答案】A
【知识点】正数和负数的认识及应用
【解析】【解答】解:由图1可知,一横表示10,一竖表示1,白色为正,黑色为负,
则图2表示的过程是计算,
故答案为:A.
【分析】根据图1的计算方法可得图2表示的过程是计算。
11.【答案】D
【知识点】正数和负数的认识及应用
【解析】【解答】由题意得:合格范围为:50﹣0.02=49.98到50+0.03=50.03,
而49.88mm<49.98mm,
故可得D不合格,
故答案为:D.
【分析】根据题意计算得到合格的范围,根据零件的加工的直径,判断其是否在合格范围之内即可得到答案。
12.【答案】16;12;15;21
【知识点】正数和负数的认识及应用
【解析】【解答】A.8+4=12,所以现在的惠灵顿时间是11月16日12时;
B.8﹣11=﹣3,24﹣3=21,所以现在的巴西利亚时间是11月15日21时,
故答案为:16,12;15,21.
【分析】根据北京时间,结合时差将时间作和或者作差得到答案即可。
13.【答案】;
【知识点】正数和负数的认识及应用
【解析】【解答】解:观察数字规律,是一负,一正,一负,一正,所以用 表示符合;
再观察分母是 , , , , 是奇数,所以用 表示奇数;
最后观察分子是 , , , , ,后一个是前一个的 倍,用 表示第 个,
所以第 个数是 ,第 个数是 .
故答案为: , .
【分析】根据数的规律,得到答案即可。
14.【答案】0.4
【知识点】正数和负数的认识及应用
【解析】【解答】解:依题可得,
面粉最重的为25+0.2kg,面粉最轻的为25-0.2kg,
∴质量最多相差:0.2-(-0.2)=0.4(kg),
故答案为:0.4.
【分析】根据题中给出面粉的波动范围,求出其中两袋相差最大的数.
【素养提升】
15.【答案】(1)+3;+4;+2;0;D
(2)解:P点位置如图1所示;
(3)解:如图2,
根据已知条件可知:
A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);
则该甲虫走过的路线长为:1+4+2+1+2=10
(4)解:由M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),
所以,5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,
所以,点A向右走2个格点,向上走2个格点到点N,
所以,N→A应记为(﹣2,﹣2)
【知识点】正数和负数的认识及应用
【解析】【解答】解:(1)图中A→C(+3,+4),B→C(+2,0),C→D(+1,﹣2);
故答案为:(+3,+4),(+2,0),D;
【分析】(1)根据向上向右走均为正,向下向左走均为负确定数据即可;
(2)根据所给的路线确定点的位置即可;
(3)根据表示的路线确定长度相加可得结果;
(4)观察点的变化情况,根据(1)即可确定点走了格数,从而确定结论.
21世纪教育网(www.21cnjy.com)
