一元一次方程复习课件[上学期]

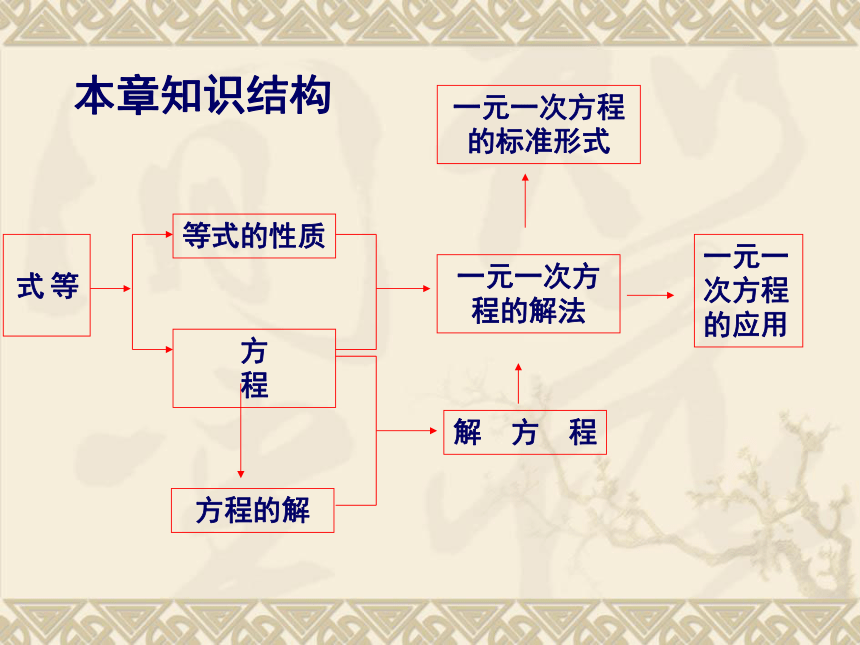
课件53张PPT。一元一次方程复习本章知识结构等 式等式的性质方 程一元一次方程的解法解一元一次方程的一般步骤变形名称注意事项去分母去括号移项合并同类项(ax=b)方程两边同除以未知数的系数a防止漏乘（尤其整数项），注意添括号；注意变号，防止漏乘；移项要变号，防止漏项；计算要仔细，不要出差错；计算要仔细，不要出差错；一、选择题1、方程 3x －5 = 7＋2 x 移项后得-------------（ ） A. 3x－2 x = 7－5 ，B. 3x＋2 x = 7－5 ， C. 3x＋2 x = 7＋5 ，D. 3x－2 x = 7＋5 ；2、方程 x －a = 7 的解是x =2，则a = --------（ ） A. 1 ， B. －1 ， C. 5 ， D. －5 ；3、方程 去分母后可得-----（ ） A. 3 x－3 =1＋2 x ，B. 3 x－9 =1＋2 x ， C. 3 x－3 =2＋2 x ，D. 3 x－12=2＋4 x ；DDB4、日历中同一竖列相邻三个数的和可以是---（ ）A 78 ， B 26 ， C 21 ， D 45 5、下列不是一元一次方程的是-------------（ ） A 4 x－1 = 2 x ， B 3x－2 x = 7 ， C x－2 = 0 ， D x = y ；6、某商品提价100%后要恢复原价，则应降价-（ ） A 30% ， B 50% ， C 75% ， D 100% ； DDB7、方程 是一元一次方程，则a和m分别为-（ ）
A 2和4 ， B －2 和 4 ，
C 2 和 －4 ， D －2 和－4 。B10、如果x=－2是方程kx+k－1=0的解，则k= 。二 解下列方程1.解：合并同类项，得：移项，得：方程两边同除以
-1，得：2.解：去括号，得：移项，得：合并同类项，得：方程两边同
除以-1，得： 解、去分母，得：去括号，得： 移项，得：合并同类项，得：方程两边同
除以-1，得：3.去分母，得：去括号，得： 移项，得：合并同类项，得：方程两边同除以13，得：解：原方程可化为：4.5、x为何值时， 的值等于-2。列方程解应用题的一般步骤 1、审题：分析题意，找出题中关键词及数量关系。
2、设元：选择一个适当的未知数用字母表示。3、列方程：根据等量关系列出方程；4、解方程，求出未知数的值；
5、检验并作答：检验求得的值是否正确、合理；写出答案。一填空题
1、一个数x的2倍减去7的差, 得36 ,列方程为____________；
2、方程5 x – 6 = 0的解是x =________；
3、日历中同一竖列相邻三个数的和为63，则这三个数分别为_____________；
4、 方程去分母得： .练 习 题2x-7=361.214、21、28.5x-10 = 2x过关斩将5、一根长18米的铁丝围成一个长是宽的2倍的 长方形,这个长方形的面积为 ；6、一件衬衫进货价60元,提高50%后标价,则标 价为 _____, 八折优惠价为______,利润 为______；18平方米90元72元12元7、鸡兔同笼共9只，腿26条, 则鸡_____只， 兔_____只；8、小明每秒钟跑4米，则他15秒钟跑___米, 2分钟跑______米,1小时跑_____公里.546048014.411 某商品现在的售价是34元，比原来的售价降低了15%，原来的售价是______.
12 三个连续偶数之和为54，则这三个偶数的积为_______
13 用一根长24cm的铁丝围成一个长方形，使它的长比宽多2cm，则长为_____.
14 某校女生占全体学生数的52%，比男生多80人，这个学校有多少学生？
15 一个梯形的下底比上底多2cm，高是5cm，面积是40cm2，求上底。
16 甲种铅笔每只0.3元，乙种铅笔每 只0.6元，用9元钱买了两种铅笔20只，两种铅笔各买了多少只？40元28807cm2000人7cm0.3x+0.6（20-x）=9x=10 20-x=10
17、小明每秒钟跑6米，小彬每秒钟跑5米，小彬站在小明前10米处，两人同时起跑，小明多少秒钟追上小彬 --------------------------------------------（ ） A 5秒， B 6秒， C 8秒， D 10秒； 18、小山上大学向某商人贷款1万元，月利率为6‰ ，
1年后需还给商人多少钱？-----------------（ ） A 17200元， B 16000元，
C 10720元， D 10600元DC 应用题
1、元旦某公园的成人的门票每张8元，儿童门票半价（即每张4元），全天共售出门票3000张，收入15600元。问这天售出儿童门票多少张？解：设售出儿童门票 x 张根据题意，得：解方程，得： x = 2100答：共售出儿童票2100张 2、某公司存入银行甲、乙两种不同性质的存款共20万元。甲种存款的年利率为1.4%，乙种存款的年利率为3.7%，该公司一年共得利息6250元，求甲、乙两种存款各多少元？解：设甲种存款为x万元。则乙种存款为（20 - x)万元根据题意得：解方程得： x = 5
所以 20 – x = 15答：甲种存款为5万元，乙种存款为15万元 3、某部队开展支农活动，甲队27人，乙队19人，现另调26人去支援，使甲队是乙队的2倍，问应调往甲队、乙队各多少人？解：设调往甲队x人，则调往乙队（26-x)人根据题意，得方程：解方程得：x = 21答：调往甲队21人。调往乙队5人。 4、日历中2×2方块的四个数的和是72，求
这四个数。解：设四个数中最小的数为x,根据题意，得方程：解方程，得：x = 14答：这四个数分别为14，15，21，22。　探　讨：5、将内径为60毫米的圆柱形长桶（已装满水）中的水向一个内径为40毫米，高为135毫米的圆柱形塑料杯倒入。当注满塑料杯时，长桶中水的高度下降多少？ 解：设长桶中水的高度下降x毫米列方程为：等量关系为：长桶下降的水的体积=塑料杯中水的体积6、一商店把货品按标价的九折出售，仍可获利12.5%，若货品进价为380元，则标价为多少元？ 两个等量关系式：售价=标价的九折售价=进价（1+利润率）若设标价为x元，根据题意，列方程得：90%· x= 380（1+12.5%）等量关系中的两售价相等7、《中华人民共和国个人所得税法》规定，公民月工资所得不超过800元（人民币）的部分不必纳税，超过800元的部分为各月应纳税所得额，超过部分的税款按下表分段累加计算：
若某人1月份应交纳此项税款121元，则他的当月工资是多少元？ 问题分析：本题应先确定该人1月份工资在哪个部分以内。解：假设他工资超过部分不超过800元，那他所付税款不超过40元，而他付了121元的税款，因此他的工资的超过部分超过800元；假设他的工资超过部分超过2000元，则他所付税款应超过200元，因此，他的工资超过部分在800元~2000元之间。设他1月份的工资收入为x元列方程为：800×5%＋（ x－800－800）×10% = 121解得：x = 2410答：该人1月份工资收入为2410元8（相遇问题） 相遇问题中，隐含的相等关系有：
⑴双方所走的路程之和等于全部路程
⑵同时出发到相遇时，双方所用时间相同 例1：甲、乙两站间的路程为360km，一列慢车从甲站开出，每小题行驶48km，一列快车从乙站开出，每小时行驶72km.
⑴两车同时开出，相向而行，多少小时相遇？解：⑴设两车行驶了x小时相遇，那么慢车行驶了48xkm，
快车行驶了72xkm
根据题意，得
48x+72x=360
120x=360
x=3
答：两车行驶了3小时相遇。例1：甲、乙两站间的路程为360km，一列慢车从甲站开出，每小题行驶48km，一列快车从乙站开出，每小时行驶72km.
⑵快车先开25分，两车相向而行，慢车行驶多少小时两车相遇？ 解：⑵设慢车行驶了x小时两车相遇，那么慢车行驶了48xkm ，快车行驶了 ,到达丙地，又行驶了72xkm ,
根据题意，得：

120x=330

答：慢车行驶了2小时45分两车相遇。
例1：甲、乙两站间的路程为360km，一列慢车从甲站开出，每小时行驶48km，一列快车从乙站开出，每小时行驶72km.
⑶若两车必须在距两城相等的站错车，则慢车比快车早开多少小时？解：设慢车比快车早开x小时，根据题意，得：



答：慢车比快车早开 小时。例1：甲、乙两站间的路程为360km，一列慢车从甲站开出，每小时行驶48km，一列快车从乙站开出，每小时行驶72km.
⑷若快车长200米，慢车长280米，从相遇到车尾离开需多少秒钟？解：设从相遇到车尾离开需x秒钟
根据题意，得：

答：从相遇到车尾离开需14.4秒。 学生练习：
1.A 、B两地相距29千米，甲A从地出发步行前往B地，48分钟后，乙从B地出发，以每小时比甲慢1千米的速度前往A地。已知甲出发3小时后与乙相遇，求乙的速度。学生练习：
2. 甲、乙二人骑自行车分别从A、B两地同时出发，相向而行，相遇时乙比甲多行12千米，如果甲每小时行14千米，乙每小时行17千米，求相遇时甲行了多少千米？
追及问题中，隐含的等量关系有：
⑴同地出发到追及时，两车所行路程相等；异地出发到追及时，两者行程之差等于两者出发点的路程；
⑵同时出发到追及时，时间相等；非同时出发到追及时，两者的时间之差等于先出发一方先用的时间。
所以，在审题时，要弄清是相向而行，还是同向而行？是同地出发，还是异地出发？是同时出发，还是谁先出发？ 9追及问题例2：一队学生去校外进行军车野营训练，他们以5千米／时的速度前进，走了18分钟的时候，学校要将一个紧急通知传给队长，通讯员从学校出发，骑自行车以14千米／时的速度按原路追上去，通讯员用多少时间可以追上学生队伍？分析：已知是什么？什么叫做“按原路追上去”？相等关系是什么？
已知是学生行进速度和通讯员骑车速度，以及学生先通讯员出发的时间。
“按原路追上去”就是“同向而行”。
相等关系是：通讯员行进路程＝学生行进路程解：设通讯员用x小时可以追上学生队伍，根据题意，得


答：通讯员用 小时（即10分钟）可以追上学生队伍。
例2：一队学生去校外进行军车野营训练，他们以5千米／时的速度前进，走了
18分钟的时候，学校要将一个紧急通知传给队长，通讯员从学校出发，骑自行车以14千米／时的速度按原路追上去，通讯员用多少时间可以追上学生队伍？变式1：若问队长出发后多少时间接到学校的通知？ 变式2：若问通讯员追上学生队伍时，他们已经行进了多少路程？ 解：设队长出发x小时后，接到学校的紧急通知。
根据题意，得

答：队长出发 小时接到学校通知。 解：设通讯员追上学生队伍时，他们已经行进了x千米。
根据题意，得

答：通讯员追上学生队伍时，他们已经行进了 千米。
变式3：一队学生去校外进行军事野营训练，他们以5千米／时的速度行进，走了18分钟的时候，学校要一名通讯员骑自行车从学校出发，并按原路追上去，用10分钟（即小时）的时间把一个紧急通知传到队长那里，通讯员必须以怎样的速度行进？解：设通讯员的速度为x千米／时，根据题意，得

x=14
答：通讯员的速度为14千米／时 变式4：一队学生去校外进行军事野营训练，在他们从学校出发走了18分钟的时候，学校要将一个紧急通知传给队长，通讯员从学校出发，骑自行车以14千米／时的速度按原路追上去，只用10分钟就追上了学生队伍，求 学生的行进速度。
解：设学生行进速度为x千米／时
依题意，得
x=5
答：学生行进速度为5千米／时。 x=72 快车的速度为72千米。 快车的速度为x千米／时 学生练习：
2. 一辆货车从A地出发前往B地，45分钟后，一辆客车也从A地出发前往B地，货车每小时行40千米，客车每小时行50千米，结果两车同时到达B地，求A、B两地间的路程。（只列方程）解：设A、B两地间的路程为千米
根据题意，得 小结：
1. 行程问题要抓住三个基本量速度、时间、路程进行审题、分析；
2. 除了充分利用题目中明确告诉的数量关系外，还应重视对隐含的相等关系的运用；
3. 列方程注意方程两边所表示的量要相同，并且各项的单位必须一致；
4. 行程问题常画直线型示意图，利用图形的直观性帮助我们分析题意，寻求相等关系。思考题：
李伟从家里骑摩托车到火车站，如果每小时行30千米，那么比火车开车时间早到15分钟，若每小时行18千米，则比火车开车时间迟到15分钟，现在李伟打算在火车开车前10分钟到达火车站，求李伟此时骑摩托车的速度应该是多少？
备用题1 把1400元奖学金按照两种奖项奖给22名学生，其中一等奖每人200元，二等奖每人50元，获得一等奖的学生有多少？
2 种一批树，如果每人种10棵，则剩6棵未种；如果每人种12棵，则缺6棵，有多少人种树？
3 某乡改种玉米为种优质杂粮后，今年农民人均收入比去年提高20%，今年人均收入比去年的1.5倍少1200吨。这个乡去年农民人均收入是多少元？
4 一架飞机在两城之间飞行，风速为24千米/时，若顺风飞行需要2小时50分，逆风飞行需要3小时，求无风时飞机的航速。200x+50（22-x）=1400 x=2X=6X（1+20%）=1.5x-1200 x=4000X=8405 甲乙二人骑车从相距65千米的两地同时出发相向而行，2小时相遇，若甲比乙每小时多走2.5千米求甲的速度。
6 甲乙二人相距80千米，他们同时出发，2小时后甲追上乙，已知乙的速度为5千米/时，求甲的速度。
7 某商品标价165元，以9折出售后仍可获利10%，求该商品的进价。
8 某个体户在一次买卖中，同时买出两件上衣，每件都以135元出售，，已知一件赢利25%，一件亏本25%，那么在这次买卖中他赢亏了多少？
9 某队参加了10场足球比赛，共积17分，已知胜一场得3分，平一场得1分，负一场得0分，其中该队输了3场，求该队胜的场次？
10 有一个两位数，它的个位上的数与十位上的数的和为10，交换个位上的数与十位上的数的位置，所得的两位数比原来的两位数大36，求原两位数11 已知五个连续整数中的三个连续奇数的和比两个偶数的和多47，求这五个连续整数。
12 甲队有78人，乙 队有63人，现从乙队抽调一部分到甲队去做某项工作，使甲队的人数是乙队的2倍，问抽调了多少人？
13 某市收取水费规定：若每户用水不超过7立方米则按每立方米1.2元收费，若超过7立方米，则超过部分按每立方米3元收费。某月老王所缴水费的平均水价为每立方米2.37元，那么老王这个月共用了多少立方米的水？
14 奶奶用20元钱买了2斤桔子、3斤苹果和4斤海棠已知桔子、苹果、海棠的单价之比为1：2：3，求每种水果的单价。15 某种商品如果按定价的七五折出售将赔25元，而按定价的九五折出售将赚20元，求定价。
16 某人到书店买书若购卡买书可获8折优惠，但办卡要交纳20元手续费。小红作为学习委员，为班集体买书，她该不该办卡？
17 某人从家里去上班，每小时行5千米，下班按原路返回，每小时比去时慢1千米，结果下班比上班多用了10分钟，求从家里到上班地点的距离。
18 某公司存入银行甲、乙两种不同性质的存款20万元，甲种存款的年利率为1.4%，乙种存款的年利率为3.7%，该公司一年共得利息6250元，求甲、乙两种存款各是多少万元？19某车间有62个工人生产汽车的甲、乙两种零件，每人每天平均能生产甲种零件12个或乙 种零件23个（每3个甲种零件和2个乙种零件配成一套），问怎样分配工人才能使生产的零件刚好配套？
20 小云到车站，若每小时行30千米，早到24分钟；若每小时行12千米，则晚到15分钟，求小云到车站的路程。
21如图，长方形被分成四块小长方形，
其中的三块的面积如图所示，求第
四块的面积。22 一项工程，甲队单独做24天完成，乙队单独做20天完成，丙队单独做30天完成。现甲乙丙三队共同完成，总工程费24000元。按所做工作计算，各队分别得多少元？
23 某工地调来72人参加挖土和运土，已知3人挖出的土1人能恰好运走，怎样分配劳动力才不窝工？
24 现有“神州行”、“家乐园”两种充值卡， “神州行”按每分钟0.6元计算，不使用不计费； “家乐园”按每分钟0.3元计费，但每月需缴座机费24元。问：一个月内，你购买哪种卡较优惠？25 某商品2002年价格比2001年上涨了25%，欲控制该商品比2001年只上涨10%，则2003年应比2002年降价的百分数是多少？
26 出租车起步价是3元（3公里以内为起步价），以后每0.5公里0.9元，某人乘出租车付了30元钱，求该出租车行驶的路程？
27 一件工作，甲单独做20小时完成，乙单独做12小时完成。现在先由甲单独做4小时，剩下部分甲乙合做，还需多少时间完成？
28 轮船在两个码头之间航行，顺水航行需要1小时40分，逆水航行需3小时，水流的速度是12千米/时，求两个码头之间的距离。29 某开发公司生产了某种新产品需要精加工后才能投放市场。现有甲、乙两个加工厂都想加工这批产品。已知甲、乙两个工厂分别每天能加工这种产品16件和24件，且知单独加工这批产品甲厂比乙厂要多用20天，又知若由甲厂单独做，公司需付甲厂每天费用80元；若由乙厂单独做，公司需付乙厂每天费用120元。
（1）求这批新产品共有多少件？
（2）若公司董事会制定了如下方案：可以由每个厂家单独完成，也可以由两个厂家同时合作完成，但在加工过程中，公司需派一名工程师到厂进行技术指导，并由厂方为其提供每天5元的午餐补助费。请你帮助公司选择一种既省时又省钱的方案，并说明理由。30某地生产的一种绿色蔬菜，在市场上直接销售，每吨利润为1000元，经粗加工后销售每吨利润可达4500元，经精加工后销售，每吨利润涨至7500元。当地一家公司收购这种蔬菜140吨，该公司的加工能力是：如果对蔬菜进行粗加工，每天可加工16吨；如果进行精加工，每天可加工6吨，但两种加工方法不能同时进行，受季节等条件限制，公司必须用15天的时间将这批蔬菜全部销售或加工完毕。为此，公司研制了三种可行方案。
方案一：将蔬菜全部进行粗加工；
方案二：尽可能多地对蔬菜进行精加工，没来得及进行加工的蔬菜，在市场上直接出售；
方案三：将一部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好用15天完成。
你认为选择哪种方案获利最多？为什么？解：假设他工资超过部分不超过800元，那他所付税款不超过40元，而他付了121元的税款，因此他的工资的超过部分超过800元；假设他的工资超过部分超过2000元，则他所付税款应超过200元，因此，他的工资超过部分在800元~2000元之间。设他1月份的工资收入为x元列方程为：800×5%＋（ x－800－800）×10% = 121解得：x = 2410答：该人1月份工资收入为2410元