24.4 解直角三角(2课时)
图片预览







文档简介
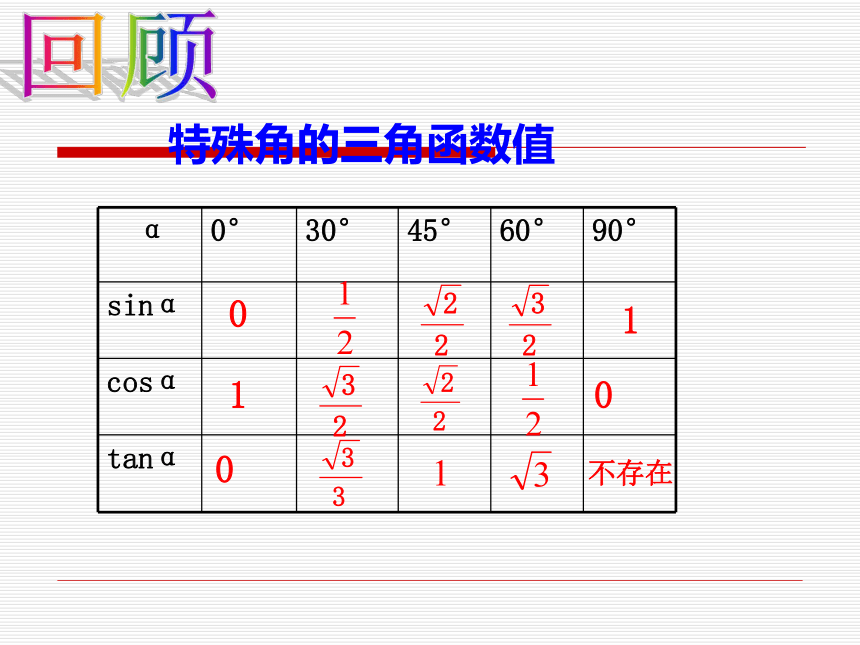
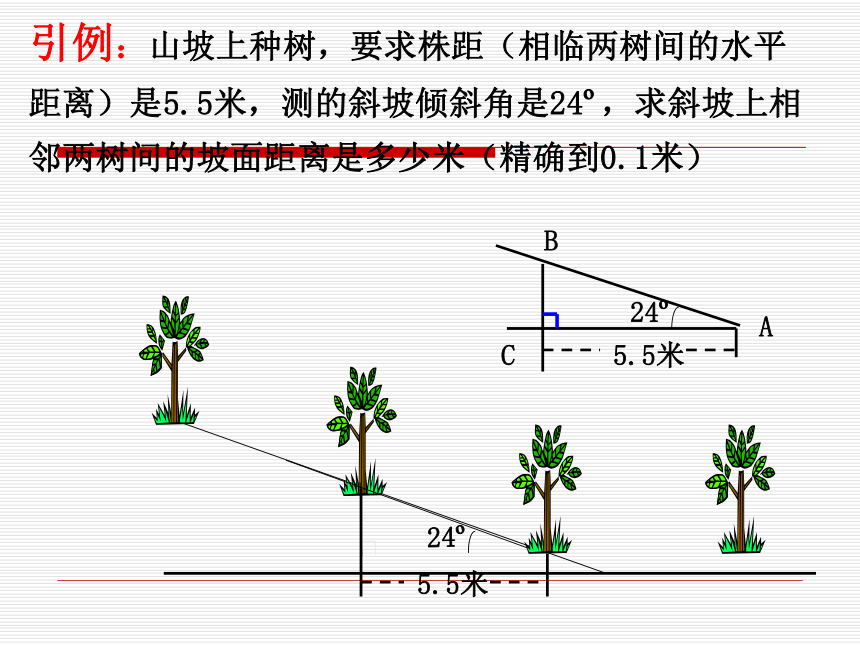
课件43张PPT。24.4 解直角三角形(1)三角函数定义回顾01100不存在特殊角的三角函数值回顾互余两角三角函数关系:sin(900-A)=cosAtanAtanB=1cos(900-A)=sinA回顾同角三角函数关系:sin2A+cos2A=1引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米) 解:在Rt△ABC中,∠C=90°引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
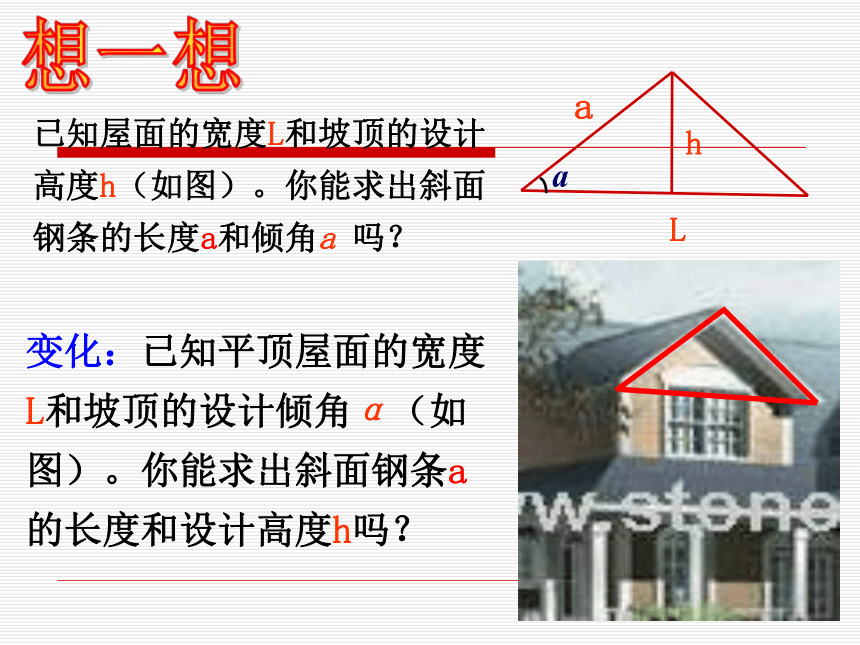
邻两树间的坡面距离是多少米(精确到0.1米)≈6.0(米)答:斜坡上相邻两树间的坡面距离是6.0米。合作探究1、已知在Rt△ABC中,∠C= Rt∠,AB=5,AC=3,求边BC的长。你能求出∠A的度数么?2、已知在Rt△ABC中, ∠C= Rt∠ ,∠A=560,AB=8,求AC的长。3、如图,在Rt△ABC中,∠C=90°(1)若∠A=30°,BC=2,求AC、AB、∠B(2)若BC=2,AB=4,求AC、∠A、∠B合作探究已知屋面的宽度L和坡顶的设计高度h(如图)。你能求出斜面钢条的长度a和倾角a 吗?想一想变化:已知平顶屋面的宽度L和坡顶的设计倾角α(如图)。你能求出斜面钢条a的长度和设计高度h吗?a 在上述例题中,我们都是利用直角三角形中的已知边、角来求出另外一些的边角.像这样,
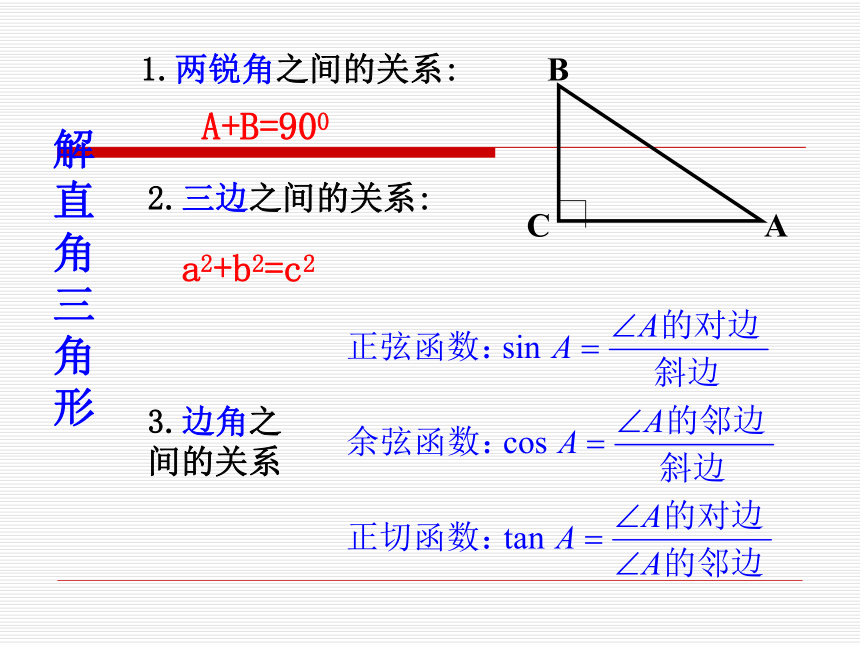
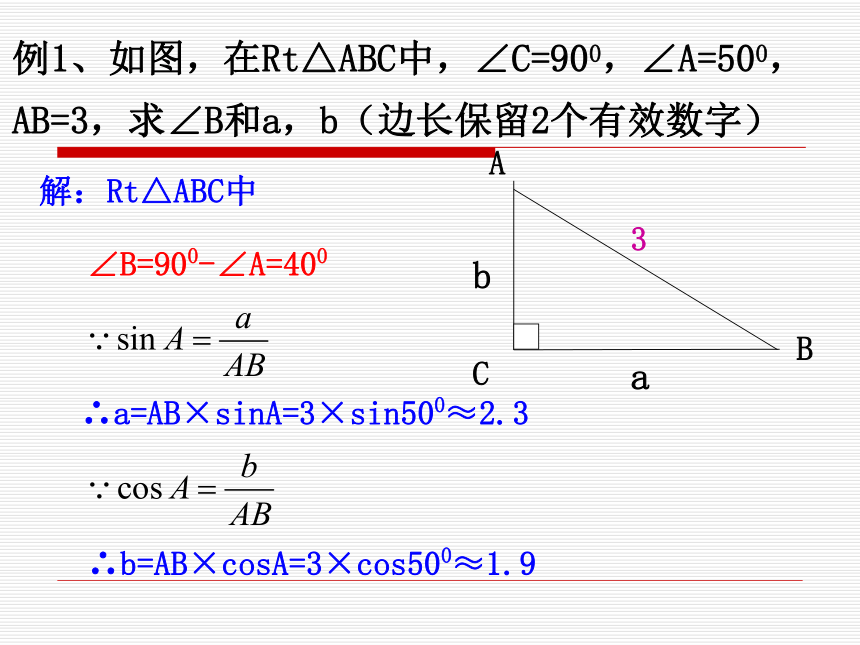
******************************** 在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=900a2+b2=c2例1、如图,在Rt△ABC中,∠C=900,∠A=500,AB=3,求∠B和a,b(边长保留2个有效数字)解:Rt△ABC中∠B=900-∠A=400∴a=AB×sinA=3×sin500≈2.3∴b=AB×cosA=3×cos500≈1.9例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°)解:在Rt△ABD中,∴α≈350.答:斜面钢条a的长度约为6.1米,坡角约为350.例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°) 在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.?解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角特别强调:(必须有一个条件是边)练一练1、在Rt△ABC中, a,b,c分别是∠A ,∠B和∠C的对边, ∠C=Rt∠,根据下列条件解直角三角形(边长保留2个有效数字,角度精确到1°)
(1) c=7 ,∠A=36 ° (2)b=10, ∠B=60 °
(3) a=5, c=7 (4)b= , cosA=2、在△ABC中,已知a,b,c分别为∠A,∠B和∠C的对边,∠C=900,根据下列条件解直角三角形(长度保留到2个有效数字,角度精确到1度)(1)c=10,∠A=30°(2)b=4,∠B=72°(3)a=5, c=7练一练(4)a=20,sinA= 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)应用练习解 在Rt△ABC中
∵∠CAB=90゜-∠DAC=50゜ 答:敌舰与A、B两炮台的距离分别约为3111米和2384米.∴BC=AB?tan∠CAB
=2000×tan50゜≈2384(米).∴ =tan∠CAB已知解直角三角形a, b∠A, a∠A, ba=b×tanA∠A, Ca=c×sinAb=c×cosA解直角三角形中的边角关系回顾整理 归纳小结1.已知,在△ABC中,∠B=45°,AC=4,BC=2 , 求sinA和AB的值。提高练习2、已知,在△ABC中,∠B=60°,∠C=45°,BC=5㎝。求AB的长。24.4 解直角三角形(2)解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=900a2+b2=c2 在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.温故知新 修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比). 记作i , 即 i = .
坡度通常写成1∶m的形式,如 i=1∶6.坡面与水平面的夹角叫做坡角,记作a,有i= = tan a.
显然,坡度越大,坡角a就越大,坡面就越陡. 试一试1、如图
1)若h=2cm, l=5cm,则i= ;
2)若i=1:1.5, h=2m,则l= ; 2、水库的横断面是梯形ABCD,迎水坡AB的坡度i=1:2,坝高h=20m,迎水坡的水平宽度= , tana= ;3m40m例1、厂房屋顶人字架(等腰三角形)的跨度为10m,角A=26?。求中柱BC(C为底边中点)和上弦AB的长(精确到0?01cm)例2、水库堤坝的横断面是梯形.测得BC长为6m,CD长为60m,斜坡的坡比为1:2,5,斜坡AB的坡比为1:3,求:(1)斜坡CD的坡角∠D和坝底的宽(角度精确到1’,宽度精确到0.1m);FE解:作BE⊥AD, CF⊥AD.在Rt△CDF中,∴∠D≈21048’∴CF=CD·sinD=60×sin21048’≈22.28(m)DF=CD·cosD=60×cos21048’≈55.71(m)∴ AE=3BE=3CF=66.84(m),∴AD=AE+BC+DF=66.84+6+55.71=128.55≈128.6(m).FE解:设横断面面积为Sm3.≈1498.9(m2),=1498.9×150=224835(m3)答:斜坡CD的坡角约为21048’,坡底宽约为128.6m,建造这个堤坝需用土石方224835m3.例2、水库堤坝的横断面是梯形.测得BC长为6m,CD长为60m,斜坡的坡比为1:2,5,斜坡AB的坡比为1:3,求:1、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m .2、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示).练一练310 3、如图一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到0.1米)练一练作DE⊥AB,CF⊥AB,垂足分别为E、 F.由题意可知: ?
DE=CF=4.2(米),CD=EF=12.51(米).
在Rt△ADE中,因为
所以 在Rt△BCF中,同理可得
因此 AB=AE+EF+BF
≈6.72+12.51+7.90
≈27.13(米).
答:路基下底的宽约为27.13米. 如图,沿水库拦水坝的背水坡将坝面加宽两米,坡度由原来的1:2改成1:2.5,已知原背水坡长BD=13.4米, 求: (1)原背水坡的坡角 和加宽后的背水坡的坡角(2)加宽后水坝的横截面面积增加了多少?(精确到0.01)1、如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.2.有一建筑物,在地面上A点测得其顶点C的仰角为300,向建筑物前进50m至B处,又测得C的仰角为450,求该建筑物的高度(结果精确到0.1m).做一做做一做3、如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=1350.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).4、横截面为等腰梯形的水库大坝,坝顶宽6m,坝高10m,斜坡AB的坡度i=1:2,为了提高大坝的储水能力,在坝顶宽度和斜坡坡度不变的情况下,加固一条长50m的大坝,需要多少土方?做一做例3、体育项目400m栏比赛中,规定相邻两栏架的路程为45m。在弯道处,以跑道离内侧0.3m处的弧线(如图中的虚线)的长度作为相邻两栏架之间的间隔路程。已知跑道的内侧线半径为36m,问在设定A栏架后,B栏架离栏架的距离是多少(π取3.14,结果精确到0.1m)解:连结AB,由题意得AB=45m, OB=36.3m作OC⊥AB于C.∵OA=OB,∴AB=AC且∠AOC∴AC=OAsin∠AOC=36.3×sin35.530≈21.09 (m)∴AB=2AC=2×21.09≈42.2(m).答:B栏架离A栏架的距离约为42.2m.练一练1、如图是一污水管的横截面,已知污水管的内径为70cm.污水的高度为10cm.求污水截面面积s.Φ7010单位: 厘米解:ABCDEO在Rt△AOE中,OA=35㎝,OE=35-10=25㎝.∴∠AOE≈44.40,∴∠AOC≈88.80∴S=S扇形OAC-S△AOC≈948.8(㎝),≈612.5(㎝2)≈948.8-612.5≈336(㎝2)答:污水截面面积约为336㎝2.2、如图,燕尾槽的横断面是一个等腰梯形ABCD,其中燕尾角∠B=550,外口宽AD=188mm,燕尾槽的深度是70mm,求它的里口宽BC(结果精确到1mmm).3、一个锥形零件的轴截面如图所示,已知倾角α=5.20, 零件的长度l=20cm,大头直径D=10cm,求小头直径d(精确到0.1cm)练一练谈谈今天的收获畅所欲言 已知在△ABC中,AB+AC=9cm,AB和AC的夹角为300,设当AB为x(cm)时,△ABC的面积为S(cm2)(1)求S关于x的函数解析式;(2)问何时△ABC的面积最大?最大面积为多少?拓展提高再见Good Bye!
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米) 解:在Rt△ABC中,∠C=90°引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米)≈6.0(米)答:斜坡上相邻两树间的坡面距离是6.0米。合作探究1、已知在Rt△ABC中,∠C= Rt∠,AB=5,AC=3,求边BC的长。你能求出∠A的度数么?2、已知在Rt△ABC中, ∠C= Rt∠ ,∠A=560,AB=8,求AC的长。3、如图,在Rt△ABC中,∠C=90°(1)若∠A=30°,BC=2,求AC、AB、∠B(2)若BC=2,AB=4,求AC、∠A、∠B合作探究已知屋面的宽度L和坡顶的设计高度h(如图)。你能求出斜面钢条的长度a和倾角a 吗?想一想变化:已知平顶屋面的宽度L和坡顶的设计倾角α(如图)。你能求出斜面钢条a的长度和设计高度h吗?a 在上述例题中,我们都是利用直角三角形中的已知边、角来求出另外一些的边角.像这样,
******************************** 在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=900a2+b2=c2例1、如图,在Rt△ABC中,∠C=900,∠A=500,AB=3,求∠B和a,b(边长保留2个有效数字)解:Rt△ABC中∠B=900-∠A=400∴a=AB×sinA=3×sin500≈2.3∴b=AB×cosA=3×cos500≈1.9例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°)解:在Rt△ABD中,∴α≈350.答:斜面钢条a的长度约为6.1米,坡角约为350.例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°) 在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.?解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角特别强调:(必须有一个条件是边)练一练1、在Rt△ABC中, a,b,c分别是∠A ,∠B和∠C的对边, ∠C=Rt∠,根据下列条件解直角三角形(边长保留2个有效数字,角度精确到1°)
(1) c=7 ,∠A=36 ° (2)b=10, ∠B=60 °
(3) a=5, c=7 (4)b= , cosA=2、在△ABC中,已知a,b,c分别为∠A,∠B和∠C的对边,∠C=900,根据下列条件解直角三角形(长度保留到2个有效数字,角度精确到1度)(1)c=10,∠A=30°(2)b=4,∠B=72°(3)a=5, c=7练一练(4)a=20,sinA= 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)应用练习解 在Rt△ABC中
∵∠CAB=90゜-∠DAC=50゜ 答:敌舰与A、B两炮台的距离分别约为3111米和2384米.∴BC=AB?tan∠CAB
=2000×tan50゜≈2384(米).∴ =tan∠CAB已知解直角三角形a, b∠A, a∠A, ba=b×tanA∠A, Ca=c×sinAb=c×cosA解直角三角形中的边角关系回顾整理 归纳小结1.已知,在△ABC中,∠B=45°,AC=4,BC=2 , 求sinA和AB的值。提高练习2、已知,在△ABC中,∠B=60°,∠C=45°,BC=5㎝。求AB的长。24.4 解直角三角形(2)解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=900a2+b2=c2 在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.温故知新 修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比). 记作i , 即 i = .
坡度通常写成1∶m的形式,如 i=1∶6.坡面与水平面的夹角叫做坡角,记作a,有i= = tan a.
显然,坡度越大,坡角a就越大,坡面就越陡. 试一试1、如图
1)若h=2cm, l=5cm,则i= ;
2)若i=1:1.5, h=2m,则l= ; 2、水库的横断面是梯形ABCD,迎水坡AB的坡度i=1:2,坝高h=20m,迎水坡的水平宽度= , tana= ;3m40m例1、厂房屋顶人字架(等腰三角形)的跨度为10m,角A=26?。求中柱BC(C为底边中点)和上弦AB的长(精确到0?01cm)例2、水库堤坝的横断面是梯形.测得BC长为6m,CD长为60m,斜坡的坡比为1:2,5,斜坡AB的坡比为1:3,求:(1)斜坡CD的坡角∠D和坝底的宽(角度精确到1’,宽度精确到0.1m);FE解:作BE⊥AD, CF⊥AD.在Rt△CDF中,∴∠D≈21048’∴CF=CD·sinD=60×sin21048’≈22.28(m)DF=CD·cosD=60×cos21048’≈55.71(m)∴ AE=3BE=3CF=66.84(m),∴AD=AE+BC+DF=66.84+6+55.71=128.55≈128.6(m).FE解:设横断面面积为Sm3.≈1498.9(m2),=1498.9×150=224835(m3)答:斜坡CD的坡角约为21048’,坡底宽约为128.6m,建造这个堤坝需用土石方224835m3.例2、水库堤坝的横断面是梯形.测得BC长为6m,CD长为60m,斜坡的坡比为1:2,5,斜坡AB的坡比为1:3,求:1、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m .2、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示).练一练310 3、如图一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到0.1米)练一练作DE⊥AB,CF⊥AB,垂足分别为E、 F.由题意可知: ?
DE=CF=4.2(米),CD=EF=12.51(米).
在Rt△ADE中,因为
所以 在Rt△BCF中,同理可得
因此 AB=AE+EF+BF
≈6.72+12.51+7.90
≈27.13(米).
答:路基下底的宽约为27.13米. 如图,沿水库拦水坝的背水坡将坝面加宽两米,坡度由原来的1:2改成1:2.5,已知原背水坡长BD=13.4米, 求: (1)原背水坡的坡角 和加宽后的背水坡的坡角(2)加宽后水坝的横截面面积增加了多少?(精确到0.01)1、如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.2.有一建筑物,在地面上A点测得其顶点C的仰角为300,向建筑物前进50m至B处,又测得C的仰角为450,求该建筑物的高度(结果精确到0.1m).做一做做一做3、如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=1350.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).4、横截面为等腰梯形的水库大坝,坝顶宽6m,坝高10m,斜坡AB的坡度i=1:2,为了提高大坝的储水能力,在坝顶宽度和斜坡坡度不变的情况下,加固一条长50m的大坝,需要多少土方?做一做例3、体育项目400m栏比赛中,规定相邻两栏架的路程为45m。在弯道处,以跑道离内侧0.3m处的弧线(如图中的虚线)的长度作为相邻两栏架之间的间隔路程。已知跑道的内侧线半径为36m,问在设定A栏架后,B栏架离栏架的距离是多少(π取3.14,结果精确到0.1m)解:连结AB,由题意得AB=45m, OB=36.3m作OC⊥AB于C.∵OA=OB,∴AB=AC且∠AOC∴AC=OAsin∠AOC=36.3×sin35.530≈21.09 (m)∴AB=2AC=2×21.09≈42.2(m).答:B栏架离A栏架的距离约为42.2m.练一练1、如图是一污水管的横截面,已知污水管的内径为70cm.污水的高度为10cm.求污水截面面积s.Φ7010单位: 厘米解:ABCDEO在Rt△AOE中,OA=35㎝,OE=35-10=25㎝.∴∠AOE≈44.40,∴∠AOC≈88.80∴S=S扇形OAC-S△AOC≈948.8(㎝),≈612.5(㎝2)≈948.8-612.5≈336(㎝2)答:污水截面面积约为336㎝2.2、如图,燕尾槽的横断面是一个等腰梯形ABCD,其中燕尾角∠B=550,外口宽AD=188mm,燕尾槽的深度是70mm,求它的里口宽BC(结果精确到1mmm).3、一个锥形零件的轴截面如图所示,已知倾角α=5.20, 零件的长度l=20cm,大头直径D=10cm,求小头直径d(精确到0.1cm)练一练谈谈今天的收获畅所欲言 已知在△ABC中,AB+AC=9cm,AB和AC的夹角为300,设当AB为x(cm)时,△ABC的面积为S(cm2)(1)求S关于x的函数解析式;(2)问何时△ABC的面积最大?最大面积为多少?拓展提高再见Good Bye!
