第十七章 勾股定理能力提升练习(含解析)
文档属性
| 名称 | 第十七章 勾股定理能力提升练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 864.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 23:55:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
勾股定理能力提升练习
一、选择题
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A =∠C-∠B
C. a =b -c D. a:b:c= 2:3:4
2.如图 17-3-10 所示,正方形ABCD的边长为1,其面积记为S ,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为图 17-3-10S ,…,按此规律继续下去,则S 的值为( )
3.如图 17-3-11 所示的是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围
成的.若AC=6,BC =5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图17-3-12 所示的“数学风车”,则这个风车的外围周长是( )
A.36B.76C.66D.12
4.在△ABC中,AB = 17,AC= 10,BC边上的高AD= 8,则边BC 的长为( )
A.21B.15C.9D.21或9
二、填空题
5.命题“如果|a|= |b|,那么a = b ”的逆命题是_,它是_(填“真”或“假”)命题.
6.如图 17-3-13 所示,在 Rt △ABC中,∠C =90°,BC =6cm,AC=8cm,按图中所示方法将△BCD
沿BD折叠,使点C落在AB边的点C'处,那么△ADC'的面积是_.
7.如图 17-3-14所示,∠AOB = 90°,OA = 25 m,OB =5m,一机器人在点 B处看见一个小球从点
A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是_m
三、解答题
8.如图 17-3-15 所示,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东 60°方向上,办公楼B位于南偏东 45°方向上.小明沿正东方向前进60m到达C处,此时测得教学楼A恰好位于正北方向,办公楼B恰好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1m).
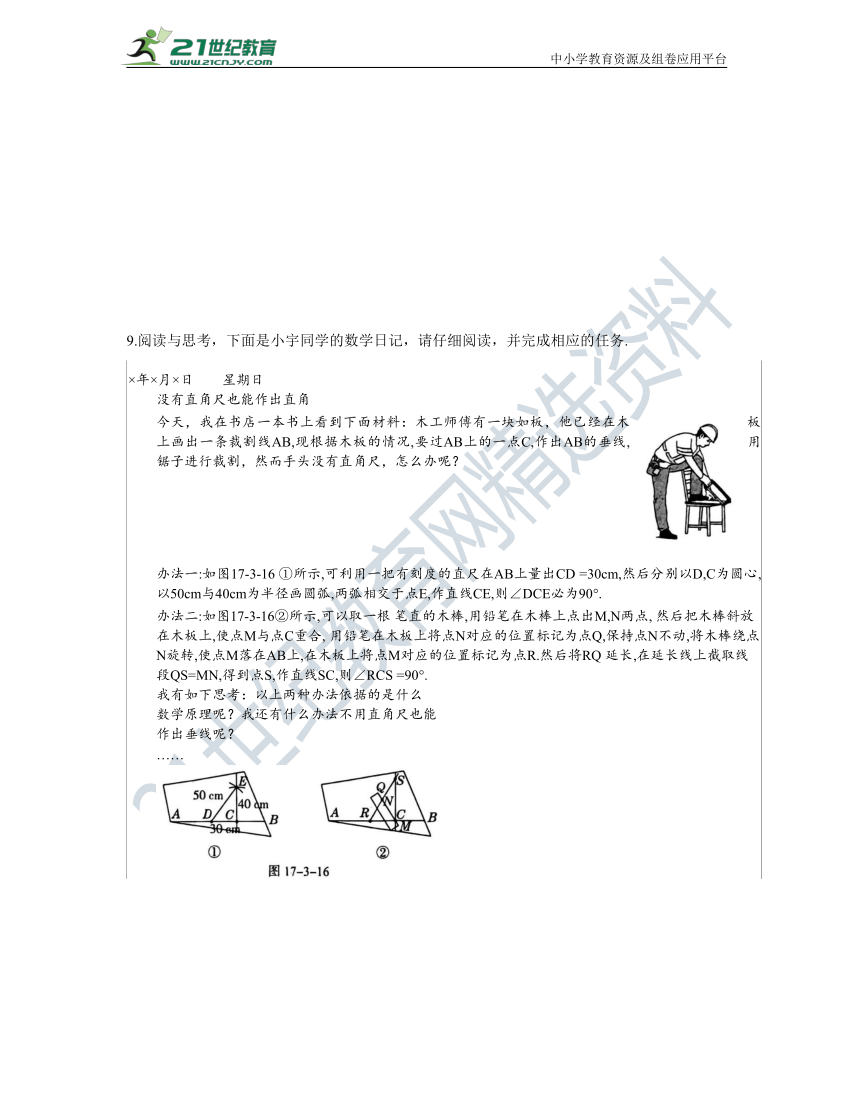
9.阅读与思考,下面是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日 星期日 没有直角尺也能作出直角 今天,我在书店一本书上看到下面材料:木工师傅有一块如板,他已经在木板上画出一条裁割线AB,现根据木板的情况,要过AB上的一点C,作出AB的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢? 办法一:如图17-3-16 ①所示,可利用一把有刻度的直尺在AB上量出CD =30cm,然后分别以D,C为圆心,以50cm与40cm为半径画圆弧,两弧相交于点E,作直线CE,则∠DCE必为90°. 办法二:如图17-3-16②所示,可以取一根 笔直的木棒,用铅笔在木棒上点出M,N两点, 然后把木棒斜放在木板上,使点M与点C重合, 用铅笔在木板上将点N对应的位置标记为点Q,保持点N不动,将木棒绕点N旋转,使点M落在AB上,在木板上将点M对应的位置标记为点R.然后将RQ 延长,在延长线上截取线段QS=MN,得到点S,作直线SC,则∠RCS =90°.
我有如下思考:以上两种办法依据的是什么
数学原理呢?我还有什么办法不用直角尺也能
作出垂线呢?
……
任务:
(1)填空:“办法一”依据的一个数学定理是_;
(2)根据“办法二”的操作过程,证明∠RCS =90°;
(3)①尺规作图:请在图 17-3-17的木板上,过点C作出AB的垂线(在木板上保留作图痕迹,不写作法);
②说明你的作法所依据的数学定理或基本事实(写出一个即可).
1. D 解析:∵∠A=∠C-∠B,∠A+∠B+∠C= 180°,
∴∠C=90°,∴△ABC是直角三角形;·
∴△ABC是直角三角形;∵a =b -c ,即b =a +c ,
∴△ABC是直角三角形;由a:b:c=2:3:4,设a=2x,b=3x,c=4x(x≠0),∵(2x) +(3x) ≠(4x) ,
∴△ABC不是直角三角形.故选项 D符合题意.
2. A 解析:在图中标上字母E,如图 D-17-14所示.
∵正方形ABCD的边长为1,
△CDE为等腰直角三角形,
∴ DE +CE = CD ,DE = CE,
∴S +S = S .
观察,发现规律:S = 1 =1,S
当n=5时, 故选 A.
3. B 解析:依题意,设“数学风车”中的四个大直角三角形的斜边长为x,则x = 12 +5 = 169,所以x=13,
所以这个风车的外围周长是(13+6)×4 = 76.
4. D 解析:
若BC边上的高AD在△ABC内部,如图D-17-15①所示,则BC= BD+CD= 15+6 = 21.
若BC边上的高AD在△ABC外部,如图D-17-15②所示,则BC = BD-CD = 15-6 = 9.
5.若a =b ,则|a|=|b| 真
6.6 cm 解析:由勾股定理可得AB = 10 cm,由折叠知 ,所以AC'= AB-BC'= 4 cm.设 CD=C'D=x cm,AD=(8-x) cm,在 Rt△ADC'中,由勾股定理,得 即x +4 =(8-x) ,解得x=3.所以
7.13 解析:设BC=xm,则AC=xm,OC=(25-x)m,由勾股定理,得BC =OB +OC ,即x = 5 +(25-x) ,
解得x= 13.即机器人行走的路程 BC 是 13 m.
8.解:由题意知,∠APC= 30°,∠BPC= 45°,AB⊥PC.
在 Rt△APC中,PC=60m,∠ACP=90°,∠APC=30°.
设AC=xm,则AP=2xm.
由勾股定理,得AP =AC +PC ,即(2x) =x +60 ,解得x≈34.64.在 Rt△BPC中,PC=60m,
∠BPC=45°,
∴∠B = 45°,∴BC =PC = 60m,
∴AB =AC+BC≈34.64+60≈94.6(m).
答:教学楼A与办公楼B之间的距离约为 94.6m .
9.(1)勾股定理的逆定理(或如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形)
(2)证明:由作图方法可知 QR = QC,QS= QC,
∴∠QCR =∠QRC,∠QCS =∠QSC.
又∵∠SRC+∠RCS+∠RSC = 180°,
∴∠QCR+∠QCS+∠QRC+∠QSC= 180°.
∴2(∠QCR+∠QCS)= 180°.
∴∠QCR+∠QCS= 90°.即∠RCS = 90°.
(3)解:①如图 D-17-16 所示,直线CP 即为所求.
②答案不唯一.如:三边分别相等ACB的两个三角形全等(或 SSS);等腰三角形顶角的平分线、底边上的高、图 D-17-16底边上的中线重合(或等腰三角形“三线合一”);到一条线段两个端点距离相等的点,在这条线段的垂直平分线上等.
勾股定理能力提升练习
一、选择题
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A =∠C-∠B
C. a =b -c D. a:b:c= 2:3:4
2.如图 17-3-10 所示,正方形ABCD的边长为1,其面积记为S ,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为图 17-3-10S ,…,按此规律继续下去,则S 的值为( )
3.如图 17-3-11 所示的是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围
成的.若AC=6,BC =5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图17-3-12 所示的“数学风车”,则这个风车的外围周长是( )
A.36B.76C.66D.12
4.在△ABC中,AB = 17,AC= 10,BC边上的高AD= 8,则边BC 的长为( )
A.21B.15C.9D.21或9
二、填空题
5.命题“如果|a|= |b|,那么a = b ”的逆命题是_,它是_(填“真”或“假”)命题.
6.如图 17-3-13 所示,在 Rt △ABC中,∠C =90°,BC =6cm,AC=8cm,按图中所示方法将△BCD
沿BD折叠,使点C落在AB边的点C'处,那么△ADC'的面积是_.
7.如图 17-3-14所示,∠AOB = 90°,OA = 25 m,OB =5m,一机器人在点 B处看见一个小球从点
A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是_m
三、解答题
8.如图 17-3-15 所示,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东 60°方向上,办公楼B位于南偏东 45°方向上.小明沿正东方向前进60m到达C处,此时测得教学楼A恰好位于正北方向,办公楼B恰好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1m).
9.阅读与思考,下面是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日 星期日 没有直角尺也能作出直角 今天,我在书店一本书上看到下面材料:木工师傅有一块如板,他已经在木板上画出一条裁割线AB,现根据木板的情况,要过AB上的一点C,作出AB的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢? 办法一:如图17-3-16 ①所示,可利用一把有刻度的直尺在AB上量出CD =30cm,然后分别以D,C为圆心,以50cm与40cm为半径画圆弧,两弧相交于点E,作直线CE,则∠DCE必为90°. 办法二:如图17-3-16②所示,可以取一根 笔直的木棒,用铅笔在木棒上点出M,N两点, 然后把木棒斜放在木板上,使点M与点C重合, 用铅笔在木板上将点N对应的位置标记为点Q,保持点N不动,将木棒绕点N旋转,使点M落在AB上,在木板上将点M对应的位置标记为点R.然后将RQ 延长,在延长线上截取线段QS=MN,得到点S,作直线SC,则∠RCS =90°.
我有如下思考:以上两种办法依据的是什么
数学原理呢?我还有什么办法不用直角尺也能
作出垂线呢?
……
任务:
(1)填空:“办法一”依据的一个数学定理是_;
(2)根据“办法二”的操作过程,证明∠RCS =90°;
(3)①尺规作图:请在图 17-3-17的木板上,过点C作出AB的垂线(在木板上保留作图痕迹,不写作法);
②说明你的作法所依据的数学定理或基本事实(写出一个即可).
1. D 解析:∵∠A=∠C-∠B,∠A+∠B+∠C= 180°,
∴∠C=90°,∴△ABC是直角三角形;·
∴△ABC是直角三角形;∵a =b -c ,即b =a +c ,
∴△ABC是直角三角形;由a:b:c=2:3:4,设a=2x,b=3x,c=4x(x≠0),∵(2x) +(3x) ≠(4x) ,
∴△ABC不是直角三角形.故选项 D符合题意.
2. A 解析:在图中标上字母E,如图 D-17-14所示.
∵正方形ABCD的边长为1,
△CDE为等腰直角三角形,
∴ DE +CE = CD ,DE = CE,
∴S +S = S .
观察,发现规律:S = 1 =1,S
当n=5时, 故选 A.
3. B 解析:依题意,设“数学风车”中的四个大直角三角形的斜边长为x,则x = 12 +5 = 169,所以x=13,
所以这个风车的外围周长是(13+6)×4 = 76.
4. D 解析:
若BC边上的高AD在△ABC内部,如图D-17-15①所示,则BC= BD+CD= 15+6 = 21.
若BC边上的高AD在△ABC外部,如图D-17-15②所示,则BC = BD-CD = 15-6 = 9.
5.若a =b ,则|a|=|b| 真
6.6 cm 解析:由勾股定理可得AB = 10 cm,由折叠知 ,所以AC'= AB-BC'= 4 cm.设 CD=C'D=x cm,AD=(8-x) cm,在 Rt△ADC'中,由勾股定理,得 即x +4 =(8-x) ,解得x=3.所以
7.13 解析:设BC=xm,则AC=xm,OC=(25-x)m,由勾股定理,得BC =OB +OC ,即x = 5 +(25-x) ,
解得x= 13.即机器人行走的路程 BC 是 13 m.
8.解:由题意知,∠APC= 30°,∠BPC= 45°,AB⊥PC.
在 Rt△APC中,PC=60m,∠ACP=90°,∠APC=30°.
设AC=xm,则AP=2xm.
由勾股定理,得AP =AC +PC ,即(2x) =x +60 ,解得x≈34.64.在 Rt△BPC中,PC=60m,
∠BPC=45°,
∴∠B = 45°,∴BC =PC = 60m,
∴AB =AC+BC≈34.64+60≈94.6(m).
答:教学楼A与办公楼B之间的距离约为 94.6m .
9.(1)勾股定理的逆定理(或如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形)
(2)证明:由作图方法可知 QR = QC,QS= QC,
∴∠QCR =∠QRC,∠QCS =∠QSC.
又∵∠SRC+∠RCS+∠RSC = 180°,
∴∠QCR+∠QCS+∠QRC+∠QSC= 180°.
∴2(∠QCR+∠QCS)= 180°.
∴∠QCR+∠QCS= 90°.即∠RCS = 90°.
(3)解:①如图 D-17-16 所示,直线CP 即为所求.
②答案不唯一.如:三边分别相等ACB的两个三角形全等(或 SSS);等腰三角形顶角的平分线、底边上的高、图 D-17-16底边上的中线重合(或等腰三角形“三线合一”);到一条线段两个端点距离相等的点,在这条线段的垂直平分线上等.
