第十八章 平行四边形综合提升训练(含解析)
文档属性
| 名称 | 第十八章 平行四边形综合提升训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 601.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 23:56:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
平行四边形综合提升训练
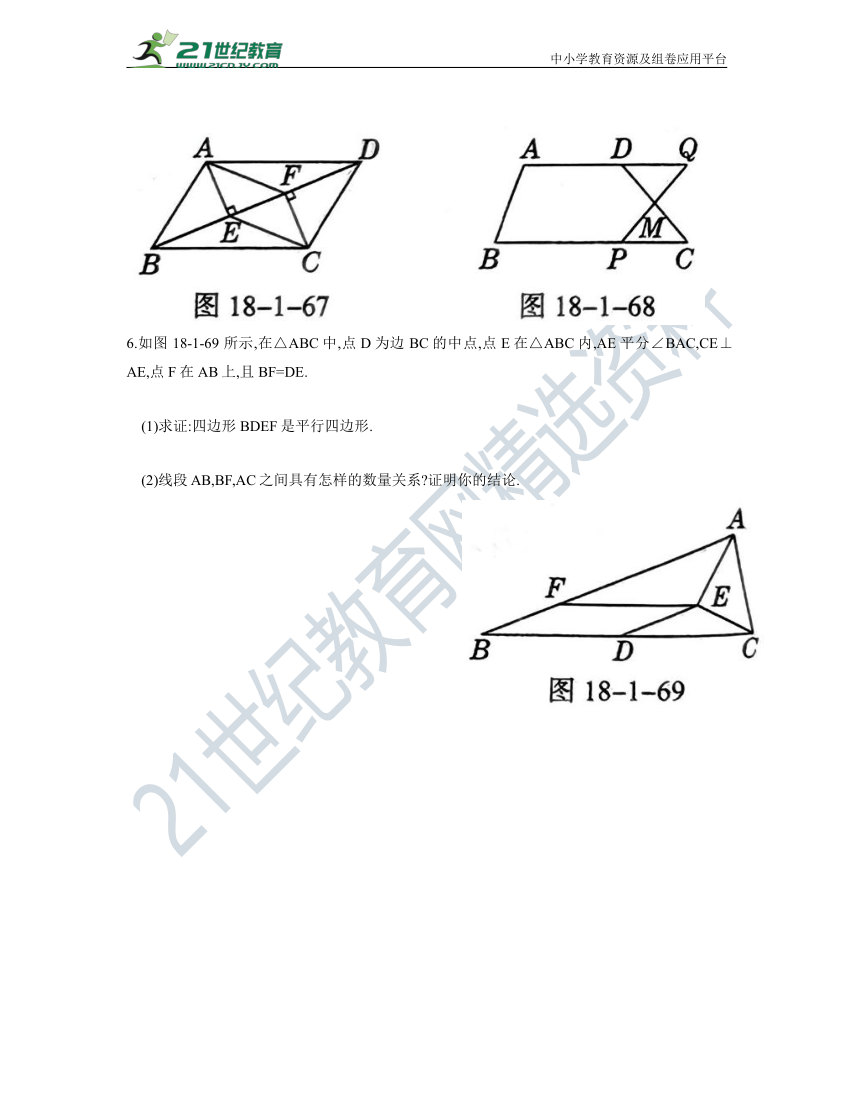
1.如图 18-1-64所示, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC = 60°, 连接OE.下列结论:
(1)AE>CE;
其中成立的有( )
A.1个B.2个C.3个D.4个
2.如图 18-1-65 所示,△ABC的周长为26,点D,E都在边 BC上,∠ABC的平分线BQ垂直于AE,垂
足为Q,∠ACB的平分线CP垂直于AD,垂足为P,若BC=10,则PQ的长为_.
3.如图 18-1-66 所示, ABCD的对角线AC与BD 相交于点 O,AE⊥BC,垂足为E, AC=2,BD =4,则AE的长为_.
4.如图 18-1-67 所示,在 ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF 是平行四边形.
(2)如果AE =3,EF=4,求AF,EC所在直线间的距离.
5.如图 18-1-68 所示,在四边形ABCD中,AD∥BC,AD=5cm,BC=9 cm. M是CD的中点,P 是BC边上的一动点(P与点 B,C不重合),连接PM并延长交AD的延长线于点 Q.
(1)试说明不管点P在 BC边上的任何位置,四边形PCQD始终是平行四边形.
(2)当点P在点B,C之间运动到什么位置时,四形ABPQ是平行四边形 并说明理由.
6.如图 18-1-69 所示,在△ABC中,点D为边 BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE.
(1)求证:四边形 BDEF是平行四边形.
(2)线段 AB,BF,AC之间具有怎样的数量关系 证明你的结论.
综合提升训练
1. A 解析:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC= 60°,∠BAD= 120°.
∵AE平分∠BAD,∴∠BAE=∠EAD=60°,
∴△ABE是等边三角形,∴AE=AB=BE,∠AEB =60°.
∴AE= CE,故①错误.∴∠EAC=∠ACE =30°,
故②错误.
∵BE = EC, ∴E为 BC 中 点, 故③错误.
∵四边形 ABCD是平行四边形,∴AO= CO,
∵AE = CE,∴EO⊥AC.
故④正确.
故成立有1个.
2.3 解析:∵△ABC的周长是26,BC= 10,
∴AB+AC= 26-10 = 16.
∵∠ABC的平分线 BQ垂直于AE,
∴在△ABQ和△EBQ中,
∴△ABQ≌△EBQ,∴AQ= EQ,AB = BE.
同理,AP=DP,AC= CD,
∴DE = BE+CD-BC= AB+AC-BC= 16-10 = 6.
∵AQ= QE,AP= DP,∴PQ是△ADE的中位线,
解析:在 ABCD中,
∴AB +AO =BO ,即△BAO是直角三角形,∠BAO= 90°.
4.(1)证明:∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB = 90°,∴AE∥CF.
在 ABCD中,∵AD∥BC,∴∠ADE=∠CBF.
又∵AD= CB,∴△ADE≌△CBF(AAS),
∴AE= CF,∴四边形AECF是平行四边形.
(2)解:在 AECF中,AF∥EC,
设AF,EC所在直线间的距离为h,∵AE⊥BD,
∴AF,EC所在直线间的距离是 2.4.
5.解:(1)如图D-18-7所示,连接DP,QC.
∵AD∥BC,∴∠QDM=∠PCM.
∵M是CD的中点,∴DM=CM.
又∵∠DMQ=∠CMP,
∴△QDM≌△PCM(ASA).
∴DQ= PC.
又∵AD∥BC,∴四边形PCQD是平行四边形.
∴ 不管点 P在BC边上任何位置,四边形 PCQD始终是行四边形.
(2)当PB=AQ时,四边形ABPQ是平行四边形.
∵ 四边形ABPQ是平行四边形,∴ BC-CP = AD+QD且CP= QD,∴9-CP =5+CP,解得 CP= 2.
∴当CP=2时,四边形ABPQ是平行四边形.
6.(1)证明:延长 CE交AB 于点 G,如图D-18-8所示.
∵AE⊥CE,
∴∠AEG=∠AEC = 90°.
∵AE平分∠BAC,
∴∠GAE=∠CAE.
在△AEG和△AEC中,
∴△AGE≌△ACE(ASA).∴ GE = EC.
∵点D为边 BC的中点,∴BD=CD,
∴DE为△CGB的中位线,∴DE∥AB.
∵DE= BF,∴ 四边形 BDEF是平行四边形.
(2)解:
理由如下:∵四边形 BDEF是平行四边形,∴BF=DE.
∵D,E分别是BC,GC的中点,
平行四边形综合提升训练
1.如图 18-1-64所示, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC = 60°, 连接OE.下列结论:
(1)AE>CE;
其中成立的有( )
A.1个B.2个C.3个D.4个
2.如图 18-1-65 所示,△ABC的周长为26,点D,E都在边 BC上,∠ABC的平分线BQ垂直于AE,垂
足为Q,∠ACB的平分线CP垂直于AD,垂足为P,若BC=10,则PQ的长为_.
3.如图 18-1-66 所示, ABCD的对角线AC与BD 相交于点 O,AE⊥BC,垂足为E, AC=2,BD =4,则AE的长为_.
4.如图 18-1-67 所示,在 ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF 是平行四边形.
(2)如果AE =3,EF=4,求AF,EC所在直线间的距离.
5.如图 18-1-68 所示,在四边形ABCD中,AD∥BC,AD=5cm,BC=9 cm. M是CD的中点,P 是BC边上的一动点(P与点 B,C不重合),连接PM并延长交AD的延长线于点 Q.
(1)试说明不管点P在 BC边上的任何位置,四边形PCQD始终是平行四边形.
(2)当点P在点B,C之间运动到什么位置时,四形ABPQ是平行四边形 并说明理由.
6.如图 18-1-69 所示,在△ABC中,点D为边 BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE.
(1)求证:四边形 BDEF是平行四边形.
(2)线段 AB,BF,AC之间具有怎样的数量关系 证明你的结论.
综合提升训练
1. A 解析:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC= 60°,∠BAD= 120°.
∵AE平分∠BAD,∴∠BAE=∠EAD=60°,
∴△ABE是等边三角形,∴AE=AB=BE,∠AEB =60°.
∴AE= CE,故①错误.∴∠EAC=∠ACE =30°,
故②错误.
∵BE = EC, ∴E为 BC 中 点, 故③错误.
∵四边形 ABCD是平行四边形,∴AO= CO,
∵AE = CE,∴EO⊥AC.
故④正确.
故成立有1个.
2.3 解析:∵△ABC的周长是26,BC= 10,
∴AB+AC= 26-10 = 16.
∵∠ABC的平分线 BQ垂直于AE,
∴在△ABQ和△EBQ中,
∴△ABQ≌△EBQ,∴AQ= EQ,AB = BE.
同理,AP=DP,AC= CD,
∴DE = BE+CD-BC= AB+AC-BC= 16-10 = 6.
∵AQ= QE,AP= DP,∴PQ是△ADE的中位线,
解析:在 ABCD中,
∴AB +AO =BO ,即△BAO是直角三角形,∠BAO= 90°.
4.(1)证明:∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB = 90°,∴AE∥CF.
在 ABCD中,∵AD∥BC,∴∠ADE=∠CBF.
又∵AD= CB,∴△ADE≌△CBF(AAS),
∴AE= CF,∴四边形AECF是平行四边形.
(2)解:在 AECF中,AF∥EC,
设AF,EC所在直线间的距离为h,∵AE⊥BD,
∴AF,EC所在直线间的距离是 2.4.
5.解:(1)如图D-18-7所示,连接DP,QC.
∵AD∥BC,∴∠QDM=∠PCM.
∵M是CD的中点,∴DM=CM.
又∵∠DMQ=∠CMP,
∴△QDM≌△PCM(ASA).
∴DQ= PC.
又∵AD∥BC,∴四边形PCQD是平行四边形.
∴ 不管点 P在BC边上任何位置,四边形 PCQD始终是行四边形.
(2)当PB=AQ时,四边形ABPQ是平行四边形.
∵ 四边形ABPQ是平行四边形,∴ BC-CP = AD+QD且CP= QD,∴9-CP =5+CP,解得 CP= 2.
∴当CP=2时,四边形ABPQ是平行四边形.
6.(1)证明:延长 CE交AB 于点 G,如图D-18-8所示.
∵AE⊥CE,
∴∠AEG=∠AEC = 90°.
∵AE平分∠BAC,
∴∠GAE=∠CAE.
在△AEG和△AEC中,
∴△AGE≌△ACE(ASA).∴ GE = EC.
∵点D为边 BC的中点,∴BD=CD,
∴DE为△CGB的中位线,∴DE∥AB.
∵DE= BF,∴ 四边形 BDEF是平行四边形.
(2)解:
理由如下:∵四边形 BDEF是平行四边形,∴BF=DE.
∵D,E分别是BC,GC的中点,
