第十八章 平行四边形能力提升练习(含解析)
文档属性
| 名称 | 第十八章 平行四边形能力提升练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 23:57:42 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
平行四边形能力提升练习
一、选择题
1.(2020·浙江温州中考)如图 18-3-21 所示,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数为( )
A.40°B.50°
C.60°D.70°
2.已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为( )
3.如图 18-3-22 所示,在正方形ABCD中,AE=AB.直线DE交 BC 于点F,则∠BED的度数是( )
A.105°B.120°C.135°D.150°
4.将矩形纸片ABCD按如图18-3-23所示的方式折叠,得到菱形 AECF.若AB=3,则BC的长为()
A.1B.2
二、填空题
5.如图 18-3-24 所示,点D,E分别是△ABC的边AB,AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=3,则DE的长为_.
6.如图 18-3-25 所示,已知面积为1的正方形ABCD的对角线相交于点 O,过点O任意作一条直线分别交AD,BC边于点E,F,则阴影部分的面积是_.
7.如图 18-3-26 所示,已知方格纸中有4个相同的正方形,则∠1+∠2+∠3=_.
8.如图 18-3-27 所示,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,AO=2,BO=3,BC
=4.将正方形沿箭头方向推,使点D落在y轴正半轴上点D处,则点C的对应点C的坐标为_.
9.如图 18-3-28 所示,在矩形ABCD中,AB =4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ
并延长,与边 BC交于点P,则线段AP=_.
三、解答题
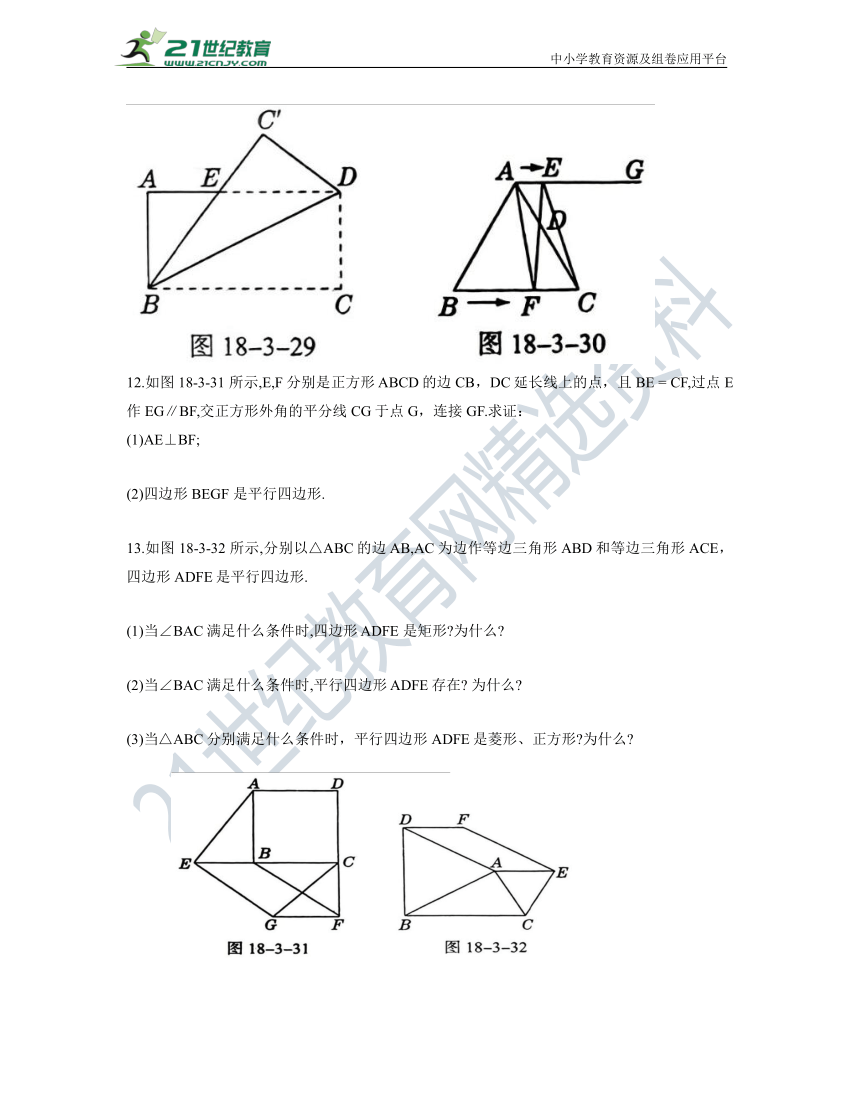
10.如图 18-3-29 所示,把矩形ABCD沿着对角线BD折叠,使点 C落在点 C'处,. '和 AD的交点为E,已知AB=4,AE=3,则BC的长是多少
11.如图 18-3-30 所示,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG
以 1 cm/s 的速度运动,同时点 F从点 B出发沿射线BC 以2cm/s的速度运动,设运动时间为t(s).
(1)连接 EF,AF,CE,当EF经过AC边的中点D时,试判断四边形 AFCE的形状并说明理由.
(2)当t为多少时,四边形ACFE 是菱形
12.如图 18-3-31 所示,E,F分别是正方形 ABCD的边 CB,DC延长线上的点,且BE = CF,过点 E作EG∥BF,交正方形外角的平分线 CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形 BEGF 是平行四边形.
13.如图 18-3-32 所示,分别以△ABC的边 AB,AC为边作等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC满足什么条件时,四边形 ADFE 是矩形 为什么
(2)当∠BAC满足什么条件时,平行四边形 ADFE存在 为什么
(3)当△ABC分别满足什么条件时,平行四边形ADFE是菱形、正方形 为什么
1. D 解析:∵在△ABC中,∠A=40°,AB =AC,∴∠C=(180°-40°)÷2 = 70°.又∵ 四边形BCDE为平行四边形,∴∠E=∠C= 70°,故选 D.
2. C 解析:如图 D-18-19 所示:
∵ 四边形ABCD是菱形, =1,OB=OD,AC⊥BD,
故选 C.
3. C 解析:∵ 四边形 ABCD 是正方形,
∴AB = AD,∠BAD =90°.
∵AB=AE,∴AE= AD.
∴ △ABE 和△ADE都是等腰三角形.
∴∠ABE =∠AEB,∠AED=∠ADE.
∵∠BAD+∠ABE+∠AEB+∠AED+∠ADE = 360°,
∴2∠AEB+2∠AED= 270°,
∠AEB+∠AED = 135°,即∠BED= 135°.
4. D 解析:设BC的长为x,则AC的长为2x,由AB +BC =AC ,即3 +x =(2x) ,解得
解析:∵D,E分别是△ABC的边AB,AC的中点,
∴DE为△ABC的中位线,
∵CF∥BE,∴四边形BCFE为平行四边形,
解析:在正方形ABCD中,OA= OC,∠OAE=∠OCF,又
7.135°解析:观察题图易得出∠1+∠3= 90°,又知∠2=45°,所以∠1+∠2+∠3= 135°.
解析:由勾股定理,得 即
∵变化后矩形变为平行四边形,即四边形: 是平行四边形,
点. 与 的纵坐标相等,∴点( 的坐标为
解析:∵在矩形ABCD中,AB=4,AD=3= BC,
∴在 Rt△ABC中,.
AD∥CP,∴CQ=5-3=2,∠CQP=∠AQD=∠ADQ=
∠CPQ.∴CP=CQ=2∴BP=3-2=1.∴Rt△ABP中,
10.解:在矩形ABCD中,∠A=90°,BC = AD,BC∥AD,
则∠CBD=∠EDB.而∠CBD=∠EBD,
∴∠EDB =∠EBD.∴ED=EB.
在 Rt△ABE中,
∴DE = 5.∴AD= AE+DE = 3+5 = 8.
故BC=AD=8.
11.解:(1)四边形 AFCE 是平行四边形.
理由:∵AG∥BC,∴∠EAD=∠DCF,∠AED=∠DFC.
∵D为AC的中点,∴AD=CD.
∴△ADE≌△CDF(AAS).∴DE = DF.
∴ 四边形AFCE 是平行四边形.
(2)若四边形ACFE 是菱形,则有 CF= AC = AE=6cm,此时的时间为6÷1= 6(s),即t= 6.
12.证明:(1)∵四边形ABCD是正方形,
∴AB = BC,∠ABC=∠BCD = 90°,
∴∠ABE=∠BCF= 90°.
在△ABE和△BCF中,
∴△ABE≌△ BCF(SAS),参
∴AE=BF,∠BAE=∠CBF.
∵EG∥BF,
∴∠CBF=∠CEG.
∵∠BAE+∠BEA= 90°,
∴∠CEG+∠BEA = 90°,
∴AE⊥EG.∵EG∥BF,
∴AE⊥BF.
(2)延长AB至点 P,使 BP =图D-18-20BE,连接EP,如图D-18-20所示,则AP = CE,∠EBP=90°,∴∠P=45°.
∵CG为正方形ABCD外角的平分线,∴∠ECG =45°,
∴∠P=∠ECG,由(1)得∠BAE =∠CEG.
在△APE和△ECG中,
∴ △APE≌△ECG(ASA),∴AE = EG.
∵AE = BF,∴EG = BF.
∵EG∥BF,∴四边形 BEGF是平行四边形.
13.解:(1)当∠BAC = 150°时,四边形ADFE 是矩形.
理由:∵△ABD和△ACE 都是等边三角形,
∴∠BAD=∠CAE =60°.
又∠BAC = 150°,∴∠DAE = 360°-∠BAD-∠CAE-∠BAC = 360°-60°-60°-150°= 90°.
又∵四边形ADFE是平行四边形,∴四边形ADFE是矩形.
(2)当∠BAC= 60°时,平行四边形ADFE 不存在.
理由:当∠BAC=60°时,∠DAE=360°-∠BAD-∠CAE-
∠BAC= 360°-60°-60°-60°= 180°,即∠DAE是平角,
AD与AE在同一条直线上,故平行四边形 ADFE不存在.
(3)当AB=AC≠BC时,平行四边形ADFE是菱形.当AB=AC,且∠BAC=150°时,平行四边形ADFE是正方形.
理由:当AB = AC≠BC时,∠BAC≠60°,即平行四边形ADFE存在.
∵△ABD和△ACE都是等边三角形,∴ AD=AB,AE=AC.又∵AB =AC,∴AD=AE,∴平行四边形ADFE
是菱形.根据以上易知,当AB=AC,且∠BAC=150°时,平行四边形ADFE是正方形.
平行四边形能力提升练习
一、选择题
1.(2020·浙江温州中考)如图 18-3-21 所示,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数为( )
A.40°B.50°
C.60°D.70°
2.已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为( )
3.如图 18-3-22 所示,在正方形ABCD中,AE=AB.直线DE交 BC 于点F,则∠BED的度数是( )
A.105°B.120°C.135°D.150°
4.将矩形纸片ABCD按如图18-3-23所示的方式折叠,得到菱形 AECF.若AB=3,则BC的长为()
A.1B.2
二、填空题
5.如图 18-3-24 所示,点D,E分别是△ABC的边AB,AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=3,则DE的长为_.
6.如图 18-3-25 所示,已知面积为1的正方形ABCD的对角线相交于点 O,过点O任意作一条直线分别交AD,BC边于点E,F,则阴影部分的面积是_.
7.如图 18-3-26 所示,已知方格纸中有4个相同的正方形,则∠1+∠2+∠3=_.
8.如图 18-3-27 所示,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,AO=2,BO=3,BC
=4.将正方形沿箭头方向推,使点D落在y轴正半轴上点D处,则点C的对应点C的坐标为_.
9.如图 18-3-28 所示,在矩形ABCD中,AB =4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ
并延长,与边 BC交于点P,则线段AP=_.
三、解答题
10.如图 18-3-29 所示,把矩形ABCD沿着对角线BD折叠,使点 C落在点 C'处,. '和 AD的交点为E,已知AB=4,AE=3,则BC的长是多少
11.如图 18-3-30 所示,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG
以 1 cm/s 的速度运动,同时点 F从点 B出发沿射线BC 以2cm/s的速度运动,设运动时间为t(s).
(1)连接 EF,AF,CE,当EF经过AC边的中点D时,试判断四边形 AFCE的形状并说明理由.
(2)当t为多少时,四边形ACFE 是菱形
12.如图 18-3-31 所示,E,F分别是正方形 ABCD的边 CB,DC延长线上的点,且BE = CF,过点 E作EG∥BF,交正方形外角的平分线 CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形 BEGF 是平行四边形.
13.如图 18-3-32 所示,分别以△ABC的边 AB,AC为边作等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC满足什么条件时,四边形 ADFE 是矩形 为什么
(2)当∠BAC满足什么条件时,平行四边形 ADFE存在 为什么
(3)当△ABC分别满足什么条件时,平行四边形ADFE是菱形、正方形 为什么
1. D 解析:∵在△ABC中,∠A=40°,AB =AC,∴∠C=(180°-40°)÷2 = 70°.又∵ 四边形BCDE为平行四边形,∴∠E=∠C= 70°,故选 D.
2. C 解析:如图 D-18-19 所示:
∵ 四边形ABCD是菱形, =1,OB=OD,AC⊥BD,
故选 C.
3. C 解析:∵ 四边形 ABCD 是正方形,
∴AB = AD,∠BAD =90°.
∵AB=AE,∴AE= AD.
∴ △ABE 和△ADE都是等腰三角形.
∴∠ABE =∠AEB,∠AED=∠ADE.
∵∠BAD+∠ABE+∠AEB+∠AED+∠ADE = 360°,
∴2∠AEB+2∠AED= 270°,
∠AEB+∠AED = 135°,即∠BED= 135°.
4. D 解析:设BC的长为x,则AC的长为2x,由AB +BC =AC ,即3 +x =(2x) ,解得
解析:∵D,E分别是△ABC的边AB,AC的中点,
∴DE为△ABC的中位线,
∵CF∥BE,∴四边形BCFE为平行四边形,
解析:在正方形ABCD中,OA= OC,∠OAE=∠OCF,又
7.135°解析:观察题图易得出∠1+∠3= 90°,又知∠2=45°,所以∠1+∠2+∠3= 135°.
解析:由勾股定理,得 即
∵变化后矩形变为平行四边形,即四边形: 是平行四边形,
点. 与 的纵坐标相等,∴点( 的坐标为
解析:∵在矩形ABCD中,AB=4,AD=3= BC,
∴在 Rt△ABC中,.
AD∥CP,∴CQ=5-3=2,∠CQP=∠AQD=∠ADQ=
∠CPQ.∴CP=CQ=2∴BP=3-2=1.∴Rt△ABP中,
10.解:在矩形ABCD中,∠A=90°,BC = AD,BC∥AD,
则∠CBD=∠EDB.而∠CBD=∠EBD,
∴∠EDB =∠EBD.∴ED=EB.
在 Rt△ABE中,
∴DE = 5.∴AD= AE+DE = 3+5 = 8.
故BC=AD=8.
11.解:(1)四边形 AFCE 是平行四边形.
理由:∵AG∥BC,∴∠EAD=∠DCF,∠AED=∠DFC.
∵D为AC的中点,∴AD=CD.
∴△ADE≌△CDF(AAS).∴DE = DF.
∴ 四边形AFCE 是平行四边形.
(2)若四边形ACFE 是菱形,则有 CF= AC = AE=6cm,此时的时间为6÷1= 6(s),即t= 6.
12.证明:(1)∵四边形ABCD是正方形,
∴AB = BC,∠ABC=∠BCD = 90°,
∴∠ABE=∠BCF= 90°.
在△ABE和△BCF中,
∴△ABE≌△ BCF(SAS),参
∴AE=BF,∠BAE=∠CBF.
∵EG∥BF,
∴∠CBF=∠CEG.
∵∠BAE+∠BEA= 90°,
∴∠CEG+∠BEA = 90°,
∴AE⊥EG.∵EG∥BF,
∴AE⊥BF.
(2)延长AB至点 P,使 BP =图D-18-20BE,连接EP,如图D-18-20所示,则AP = CE,∠EBP=90°,∴∠P=45°.
∵CG为正方形ABCD外角的平分线,∴∠ECG =45°,
∴∠P=∠ECG,由(1)得∠BAE =∠CEG.
在△APE和△ECG中,
∴ △APE≌△ECG(ASA),∴AE = EG.
∵AE = BF,∴EG = BF.
∵EG∥BF,∴四边形 BEGF是平行四边形.
13.解:(1)当∠BAC = 150°时,四边形ADFE 是矩形.
理由:∵△ABD和△ACE 都是等边三角形,
∴∠BAD=∠CAE =60°.
又∠BAC = 150°,∴∠DAE = 360°-∠BAD-∠CAE-∠BAC = 360°-60°-60°-150°= 90°.
又∵四边形ADFE是平行四边形,∴四边形ADFE是矩形.
(2)当∠BAC= 60°时,平行四边形ADFE 不存在.
理由:当∠BAC=60°时,∠DAE=360°-∠BAD-∠CAE-
∠BAC= 360°-60°-60°-60°= 180°,即∠DAE是平角,
AD与AE在同一条直线上,故平行四边形 ADFE不存在.
(3)当AB=AC≠BC时,平行四边形ADFE是菱形.当AB=AC,且∠BAC=150°时,平行四边形ADFE是正方形.
理由:当AB = AC≠BC时,∠BAC≠60°,即平行四边形ADFE存在.
∵△ABD和△ACE都是等边三角形,∴ AD=AB,AE=AC.又∵AB =AC,∴AD=AE,∴平行四边形ADFE
是菱形.根据以上易知,当AB=AC,且∠BAC=150°时,平行四边形ADFE是正方形.
