第十八章 平行四边形综合提升训练(含解析)
文档属性
| 名称 | 第十八章 平行四边形综合提升训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 796.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
特殊的平行四边形综合提升训练
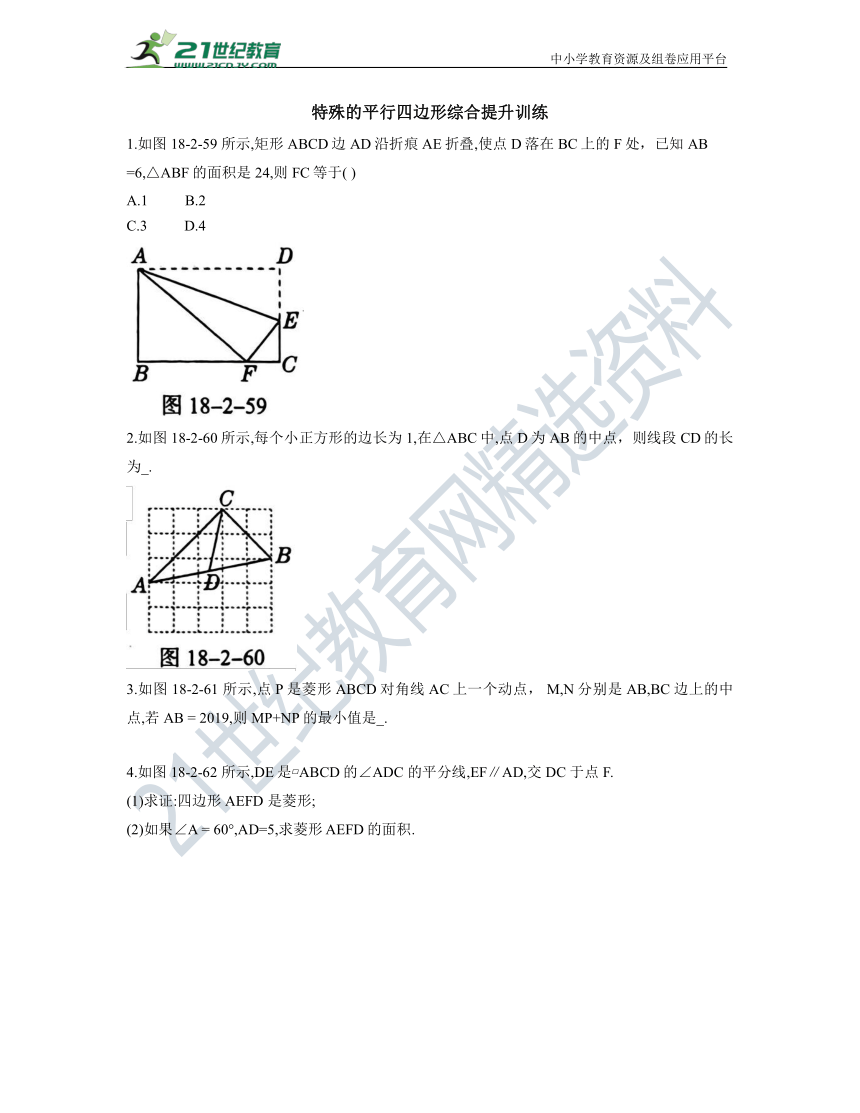
1.如图 18-2-59 所示,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB
=6,△ABF的面积是 24,则FC等于( )
A.1 B.2
C.3 D.4
2.如图 18-2-60所示,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为_.
3.如图 18-2-61 所示,点P是菱形ABCD对角线AC上一个动点, M,N分别是AB,BC边上的中点,若AB = 2019,则MP+NP 的最小值是_.
4.如图 18-2-62 所示,DE是 ABCD的∠ADC 的平分线,EF∥AD,交DC 于点 F.
(1)求证:四边形AEFD 是菱形;
(2)如果∠A = 60°,AD=5,求菱形 AEFD的面积.
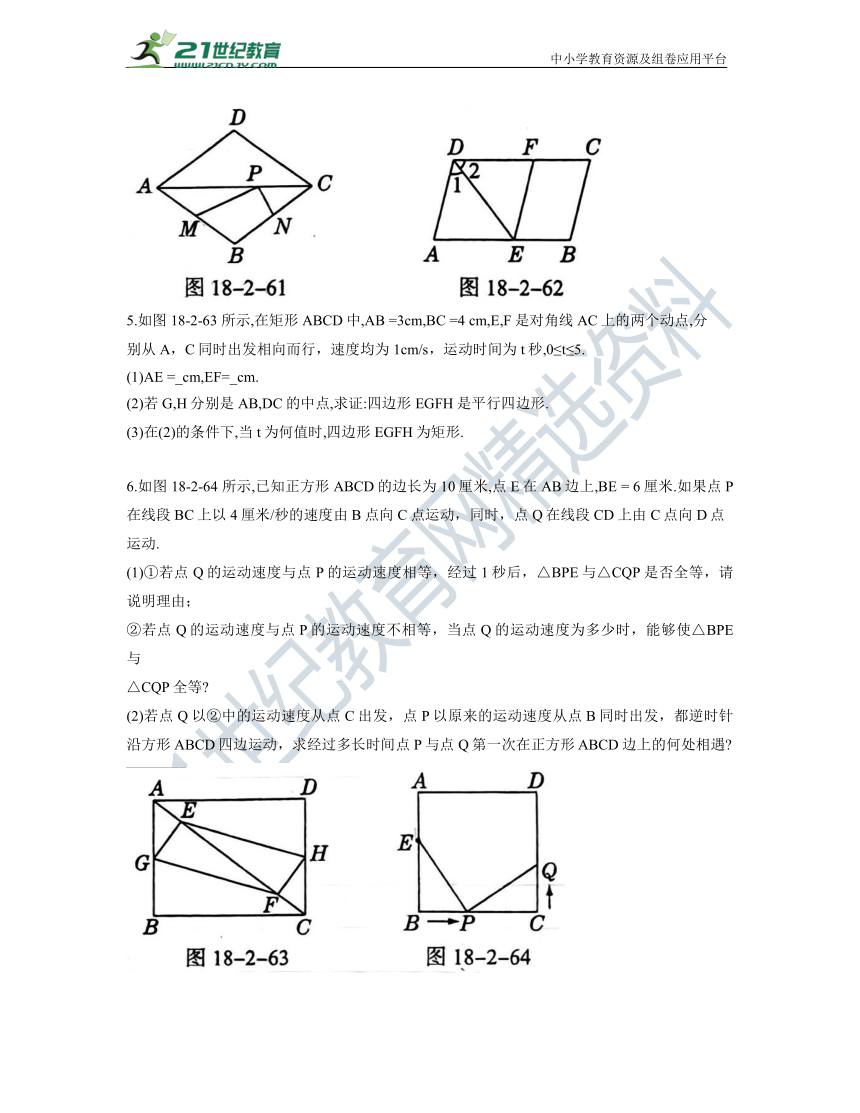
5.如图 18-2-63 所示,在矩形ABCD中,AB =3cm,BC =4 cm,E,F是对角线AC上的两个动点,分
别从A,C同时出发相向而行,速度均为1cm/s,运动时间为 t秒,0≤t≤5.
(1)AE =_cm,EF=_cm.
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形.
(3)在(2)的条件下,当t为何值时,四边形 EGFH为矩形.
6.如图 18-2-64 所示,已知正方形ABCD的边长为10厘米,点E在AB边上,BE = 6厘米.如果点P在线段BC上以4厘米/秒的速度由 B点向C点运动,同时,点Q在线段 CD上由 C点向 D点
运动.
(1)①若点 Q的运动速度与点 P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
②若点 Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与
△CQP全等
(2)若点 Q以②中的运动速度从点 C出发,点P以原来的运动速度从点B同时出发,都逆时针沿方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形 ABCD边上的何处相遇
综合提升训练
B 解析:∵四边形ABCD是矩形,∴∠B = 90°,AD=BC.∵AB=6,△ABF的面积是24,∴BF =8.由勾股定理可得 由折叠的性质,得AD=AF= 10,即BC=AD= 10,
∴FC=BC-BF= 10-8 =2.
解析:
为直角三角形,且∠ACB = 90°.又∵D为AB边的中点,
3.2 019 解析:∵菱形的对角线所在的直线是菱形的对称轴,∴ 作点M关于AC的对称点 M,连接M'N交AC于P(图略),此时MP+NP = M'N,且为最小值.∵ 菱形ABCD关于AC对称,M是AB边上的中点,∴ M'是AD的中点.又N是 BC边上的中点,∴AM'∥BN,AM'=BN,∴ 四边形 AM'NB 是平行四边形,∴ M'N= AB =2019,即 MP+NP的最小值是 2 019.
4.(1)证明:∵DF∥AE,EF∥AD,∴ 四边形 AEFD是平行四边形.∵DF∥AE,∴∠2=∠AED.
又∵∠1=∠2,∴∠AED=∠1,∴AD=AE,
∴四边形AEFD是菱形.
(2)解:∵∠A= 60°,
∴△AED为等边三角形.
∴DE= AD= 5.
如图D-18-17 所示,连接AF与DE 相交于点O,则
5.(1)解:∵ 四边形 ABCD是矩形,∴∠B = 90°,
由题意得AE = CF=tcm,
∴EF=AC-AE-CF=(5-2t) cm.故答案为t,5-2t.
(2)证明:∵四边形ABCD是矩形,
∴AB = CD,AB∥CD,AD∥BC,∠B =90°,
∵G,H分别是AB,DC的中点,
∴AG= BG,CH = DH,∴AG= CH.
∵AE= CF,∴AF= CE,∴△AFG≌△CEH(SAS),
∴ GF = HE.同理,GE = HF.
∴ 四边形 EGFH是平行四边形.
(3)解:如图 D-18-18 所示,连接GH,由(1)可知四边形 EGFH是平行四边形.
∵点G,H分别是矩形ABCD的边AB,DC的中点,∴GH=BC=4cm,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE= CF=tcm,EF=5-2t= 4(cm),解得t= 0.5(s);
②AE= CF=tcm,EF=5-2(5-t)=4(cm),解得t=4.5(s).
即当t为 0.5s或4.5s时,四边形 EGFH是矩形.
6.解:(1)①全等.理由:∵运动了 1 秒,∴ BP = CQ =4×1 =4(厘米).∵正方形ABCD中,边长为 10厘米,
∴ PC= BE = 6厘米.又∵四边形ABCD为正方形,
∴∠B=∠C,∴△BPE≌△ CQP.
②∵vp≠vQ,∴BP≠CQ.
又∵△BPE与△CQP全等,∠B =∠C,∴BP=PC,
而
(厘米/秒).
(2)设经过x秒后点 P与点 Q第一次相遇.
由题意,得 4.8x-4x = 30,解得
∴ 点 P共运动了 (厘米),∴点 P,Q在A点相遇,即经过 秒点 P与点 Q第一次在A点相遇.
特殊的平行四边形综合提升训练
1.如图 18-2-59 所示,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB
=6,△ABF的面积是 24,则FC等于( )
A.1 B.2
C.3 D.4
2.如图 18-2-60所示,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为_.
3.如图 18-2-61 所示,点P是菱形ABCD对角线AC上一个动点, M,N分别是AB,BC边上的中点,若AB = 2019,则MP+NP 的最小值是_.
4.如图 18-2-62 所示,DE是 ABCD的∠ADC 的平分线,EF∥AD,交DC 于点 F.
(1)求证:四边形AEFD 是菱形;
(2)如果∠A = 60°,AD=5,求菱形 AEFD的面积.
5.如图 18-2-63 所示,在矩形ABCD中,AB =3cm,BC =4 cm,E,F是对角线AC上的两个动点,分
别从A,C同时出发相向而行,速度均为1cm/s,运动时间为 t秒,0≤t≤5.
(1)AE =_cm,EF=_cm.
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形.
(3)在(2)的条件下,当t为何值时,四边形 EGFH为矩形.
6.如图 18-2-64 所示,已知正方形ABCD的边长为10厘米,点E在AB边上,BE = 6厘米.如果点P在线段BC上以4厘米/秒的速度由 B点向C点运动,同时,点Q在线段 CD上由 C点向 D点
运动.
(1)①若点 Q的运动速度与点 P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
②若点 Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与
△CQP全等
(2)若点 Q以②中的运动速度从点 C出发,点P以原来的运动速度从点B同时出发,都逆时针沿方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形 ABCD边上的何处相遇
综合提升训练
B 解析:∵四边形ABCD是矩形,∴∠B = 90°,AD=BC.∵AB=6,△ABF的面积是24,∴BF =8.由勾股定理可得 由折叠的性质,得AD=AF= 10,即BC=AD= 10,
∴FC=BC-BF= 10-8 =2.
解析:
为直角三角形,且∠ACB = 90°.又∵D为AB边的中点,
3.2 019 解析:∵菱形的对角线所在的直线是菱形的对称轴,∴ 作点M关于AC的对称点 M,连接M'N交AC于P(图略),此时MP+NP = M'N,且为最小值.∵ 菱形ABCD关于AC对称,M是AB边上的中点,∴ M'是AD的中点.又N是 BC边上的中点,∴AM'∥BN,AM'=BN,∴ 四边形 AM'NB 是平行四边形,∴ M'N= AB =2019,即 MP+NP的最小值是 2 019.
4.(1)证明:∵DF∥AE,EF∥AD,∴ 四边形 AEFD是平行四边形.∵DF∥AE,∴∠2=∠AED.
又∵∠1=∠2,∴∠AED=∠1,∴AD=AE,
∴四边形AEFD是菱形.
(2)解:∵∠A= 60°,
∴△AED为等边三角形.
∴DE= AD= 5.
如图D-18-17 所示,连接AF与DE 相交于点O,则
5.(1)解:∵ 四边形 ABCD是矩形,∴∠B = 90°,
由题意得AE = CF=tcm,
∴EF=AC-AE-CF=(5-2t) cm.故答案为t,5-2t.
(2)证明:∵四边形ABCD是矩形,
∴AB = CD,AB∥CD,AD∥BC,∠B =90°,
∵G,H分别是AB,DC的中点,
∴AG= BG,CH = DH,∴AG= CH.
∵AE= CF,∴AF= CE,∴△AFG≌△CEH(SAS),
∴ GF = HE.同理,GE = HF.
∴ 四边形 EGFH是平行四边形.
(3)解:如图 D-18-18 所示,连接GH,由(1)可知四边形 EGFH是平行四边形.
∵点G,H分别是矩形ABCD的边AB,DC的中点,∴GH=BC=4cm,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE= CF=tcm,EF=5-2t= 4(cm),解得t= 0.5(s);
②AE= CF=tcm,EF=5-2(5-t)=4(cm),解得t=4.5(s).
即当t为 0.5s或4.5s时,四边形 EGFH是矩形.
6.解:(1)①全等.理由:∵运动了 1 秒,∴ BP = CQ =4×1 =4(厘米).∵正方形ABCD中,边长为 10厘米,
∴ PC= BE = 6厘米.又∵四边形ABCD为正方形,
∴∠B=∠C,∴△BPE≌△ CQP.
②∵vp≠vQ,∴BP≠CQ.
又∵△BPE与△CQP全等,∠B =∠C,∴BP=PC,
而
(厘米/秒).
(2)设经过x秒后点 P与点 Q第一次相遇.
由题意,得 4.8x-4x = 30,解得
∴ 点 P共运动了 (厘米),∴点 P,Q在A点相遇,即经过 秒点 P与点 Q第一次在A点相遇.
