23.1 特殊角的三角函数值教案
图片预览


文档简介
特殊角的三角函数值
教学目标
教学知识点
1.巩固锐角三角函数的定义,进一步体会三角函数的意义.
2.经历探索30°、45°、60°的三角函数值的过程,能够进行有关的推理。
3.能够进行30°、45°、60°角的三角函数值的计算.
4.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
(二)思维训练要求
1.经历探索30°、45°、60°角的三角函数值的过程,培养学生观察、分析、发现的能力.
2.培养学生把实际问题转化为数学问题的能力.
(三)情感与价值观要求
1.积极参与数学活动,对数学产生好奇心,培养学生独立思考问题的习惯.
2.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教具重点
1.探索30°、45°、60°角的三角函数值.
2.能够进行含30°、45°、60°角的三角函数值的计算.
3.比较锐角三角函数值的大小.
教学难点
熟练掌握30°、45°、60°的三角函数值;进一步体会锐角三角函数的意义.应用锐角三角函数的边角关系解决问题。
教学方法
自主探索法
教学准备
一副三角尺 多媒体演示
教学过程
温故知新
锐角三角函数定义
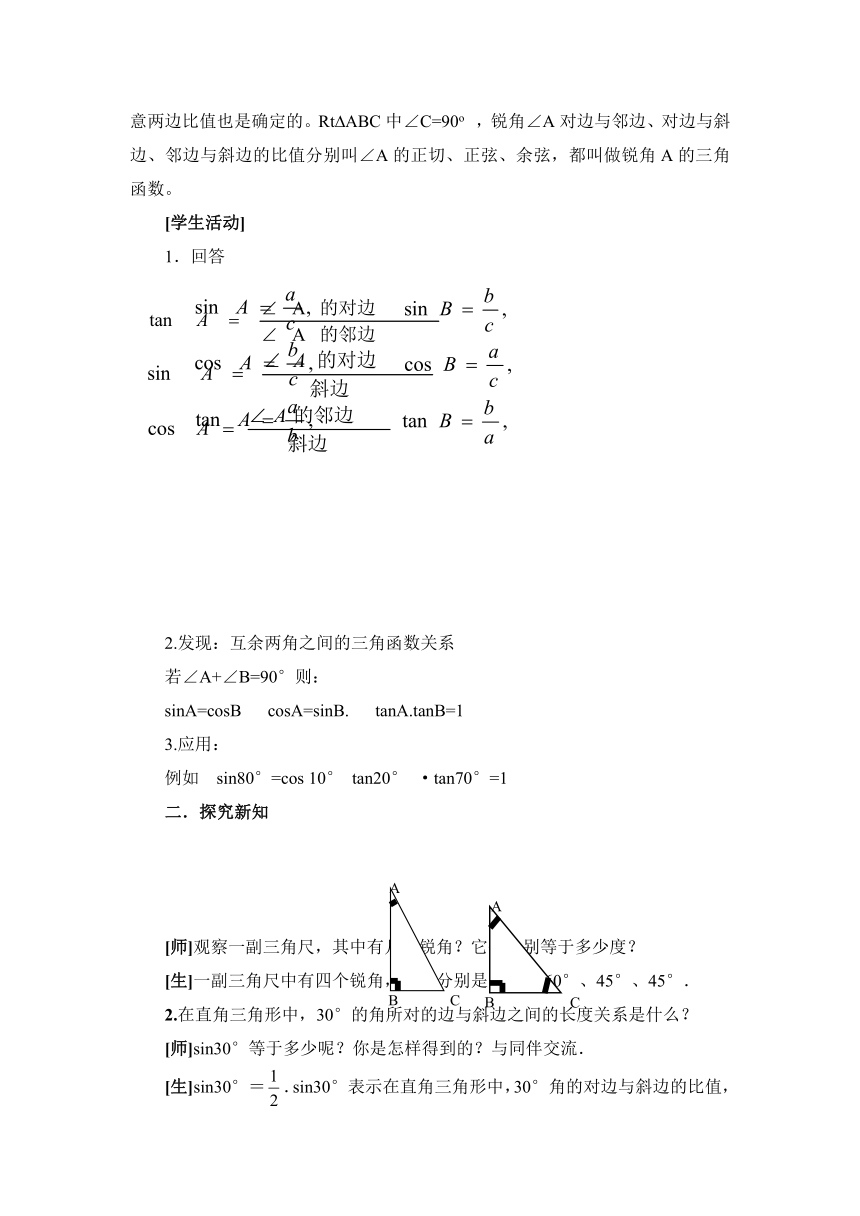
[师]我们前面学习了三角函数的定义,如果一个角的大小确定,那么它的任意两边比值也是确定的。Rt?ABC中∠C=90o ,锐角∠A对边与邻边、对边与斜边、邻边与斜边的比值分别叫∠A的正切、正弦、余弦,都叫做锐角A的三角函数。
[学生活动]
1.回答
2.发现:互余两角之间的三角函数关系
若∠A+∠B=90°则:
sinA=cosB cosA=sinB. tanA.tanB=1
应用:
例如 sin80°=cos 10° tan20° ·tan70°=1
二.探究新知
[师]观察一副三角尺,其中有几个锐角?它们分别等于多少度?
[生]一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.
2.在直角三角形中,30°的角所对的边与斜边之间的长度关系是什么?
[师]sin30°等于多少呢?你是怎样得到的?与同伴交流.
[生]sin30°=.sin30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.我们不妨设30°角所对的边为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,则斜边等于2a.根据勾股定理,可知30°角的邻边为a,所以sin30°=.
[师]cos30°等于多少?tan30°呢?
[生]cos30°=.
tan30°=.
[师]我们求出了30°角的三个三角函数值,还有两个特殊角——45°、60°,它们的三角函数值分别是多少?你是如何得到的?
[生]求60°的三角函数值可以利用求30°角三角函数值的三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.利用上图,很容易求得
sin60°=,
cos60°=,
tan60°=.
[生]也可以利用我们前面得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知
sin60°=cos(90°-60°)=cos30°=,
cos60°=sin(90°-60°)=sin30°=.
[师生共析]我们一同来求45°角的三角函数值.含45°角的直角三角形是等腰直角三角形.(如图)设其中一条直角边为a,则另一条直角边也为a,斜边为a.由此可求得
sin45°=,
cos45°=,
tan45°==1.
[师]下面请同学们完成下表:
30°、45°、60°角的三角函数值
三角函数角
锐角α
sinα
cosα
tanα
30°
45°
1
60°
这个表格中的30°、45°、60°角的三角函数值需熟记,另一方面,要能够根据30°、45°、60°角的三角函数值,说出相应的锐角的大小.
为了帮助大家记忆,我们观察表格中函数值的特点.先看第一列30°、45°、60°角的正弦值,你能发现什么规律呢?
[生]30°、45°、60°角的正弦值分母都为2,分子从小到大分别为1,,随着角度的增大,正弦值在逐渐增大.
[师]再来看第二列函数值,有何特点呢?
[生]第二列是30°、45°、60°角的余弦值,它们的分母也都是2,而分子从大到小分别为,,1,余弦值随角度的增大而减小.
[师]第三列呢?
[生]第三列是30°、45°、60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.
[师]很好,掌握了上述规律,记忆就方便多了.下面同桌之间可互相检查一下对30°、45°、60°角的三角函数值的记忆情况.相信同学们一定做得很棒.
例题讲解
学一学
例4 计算:
(1)2sin60°+3tan30°+tan45°
(2) cos245°+tan60°cos30°
.分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角三角函数值进行计算时,一般不取近似值,另外cos260°表示(cos60°)2.
解:(1)2sin60°+3tan30°+tan45°=2×+3×+1=2+1
(2) cos245°+tan60°cos30°=()2+×==2.
想一想1、tan∠A= ∠A= °.
2、sin(90°- α)= , α= ° .
Rt?ABC中∠C=90o ,sinA= ,cosB=
. 比较大小:sin50° sin40°,cos20° cos15°,
tan25° tan35°,sin40° cos50 °
能力提升
1.Rt?ABC中∠C=90o求证:sin2A+cos2A=1
2、 ABCD中∠A=60°,AB=6 AD=4.求平行四边形面积。
五.随堂练习
(1)sin60°-cos45°;(2)cos60°+tan60°;
六.小 结
我学会了什么?
七.作 业
1、P122 习题23.1 第1题
2、自选作业。
板书设计:
锐角三角函数
1.
2.30°,45°,60°角的三角函数值列表如下:
三角函数
角α
sinα
cosα
tanα
30°
45°
1
60°
课后反思:
锐角三角函数(三)
教学设计
时间:2014年11月21日
班级:九(2)班
褚集初级中学 马骏
教学目标
教学知识点
1.巩固锐角三角函数的定义,进一步体会三角函数的意义.
2.经历探索30°、45°、60°的三角函数值的过程,能够进行有关的推理。
3.能够进行30°、45°、60°角的三角函数值的计算.
4.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
(二)思维训练要求
1.经历探索30°、45°、60°角的三角函数值的过程,培养学生观察、分析、发现的能力.
2.培养学生把实际问题转化为数学问题的能力.
(三)情感与价值观要求
1.积极参与数学活动,对数学产生好奇心,培养学生独立思考问题的习惯.
2.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教具重点
1.探索30°、45°、60°角的三角函数值.
2.能够进行含30°、45°、60°角的三角函数值的计算.
3.比较锐角三角函数值的大小.
教学难点
熟练掌握30°、45°、60°的三角函数值;进一步体会锐角三角函数的意义.应用锐角三角函数的边角关系解决问题。
教学方法
自主探索法
教学准备
一副三角尺 多媒体演示
教学过程
温故知新
锐角三角函数定义
[师]我们前面学习了三角函数的定义,如果一个角的大小确定,那么它的任意两边比值也是确定的。Rt?ABC中∠C=90o ,锐角∠A对边与邻边、对边与斜边、邻边与斜边的比值分别叫∠A的正切、正弦、余弦,都叫做锐角A的三角函数。
[学生活动]
1.回答
2.发现:互余两角之间的三角函数关系
若∠A+∠B=90°则:
sinA=cosB cosA=sinB. tanA.tanB=1
应用:
例如 sin80°=cos 10° tan20° ·tan70°=1
二.探究新知
[师]观察一副三角尺,其中有几个锐角?它们分别等于多少度?
[生]一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.
2.在直角三角形中,30°的角所对的边与斜边之间的长度关系是什么?
[师]sin30°等于多少呢?你是怎样得到的?与同伴交流.
[生]sin30°=.sin30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.我们不妨设30°角所对的边为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,则斜边等于2a.根据勾股定理,可知30°角的邻边为a,所以sin30°=.
[师]cos30°等于多少?tan30°呢?
[生]cos30°=.
tan30°=.
[师]我们求出了30°角的三个三角函数值,还有两个特殊角——45°、60°,它们的三角函数值分别是多少?你是如何得到的?
[生]求60°的三角函数值可以利用求30°角三角函数值的三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.利用上图,很容易求得
sin60°=,
cos60°=,
tan60°=.
[生]也可以利用我们前面得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知
sin60°=cos(90°-60°)=cos30°=,
cos60°=sin(90°-60°)=sin30°=.
[师生共析]我们一同来求45°角的三角函数值.含45°角的直角三角形是等腰直角三角形.(如图)设其中一条直角边为a,则另一条直角边也为a,斜边为a.由此可求得
sin45°=,
cos45°=,
tan45°==1.
[师]下面请同学们完成下表:
30°、45°、60°角的三角函数值
三角函数角
锐角α
sinα
cosα
tanα
30°
45°
1
60°
这个表格中的30°、45°、60°角的三角函数值需熟记,另一方面,要能够根据30°、45°、60°角的三角函数值,说出相应的锐角的大小.
为了帮助大家记忆,我们观察表格中函数值的特点.先看第一列30°、45°、60°角的正弦值,你能发现什么规律呢?
[生]30°、45°、60°角的正弦值分母都为2,分子从小到大分别为1,,随着角度的增大,正弦值在逐渐增大.
[师]再来看第二列函数值,有何特点呢?
[生]第二列是30°、45°、60°角的余弦值,它们的分母也都是2,而分子从大到小分别为,,1,余弦值随角度的增大而减小.
[师]第三列呢?
[生]第三列是30°、45°、60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.
[师]很好,掌握了上述规律,记忆就方便多了.下面同桌之间可互相检查一下对30°、45°、60°角的三角函数值的记忆情况.相信同学们一定做得很棒.
例题讲解
学一学
例4 计算:
(1)2sin60°+3tan30°+tan45°
(2) cos245°+tan60°cos30°
.分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角三角函数值进行计算时,一般不取近似值,另外cos260°表示(cos60°)2.
解:(1)2sin60°+3tan30°+tan45°=2×+3×+1=2+1
(2) cos245°+tan60°cos30°=()2+×==2.
想一想1、tan∠A= ∠A= °.
2、sin(90°- α)= , α= ° .
Rt?ABC中∠C=90o ,sinA= ,cosB=
. 比较大小:sin50° sin40°,cos20° cos15°,
tan25° tan35°,sin40° cos50 °
能力提升
1.Rt?ABC中∠C=90o求证:sin2A+cos2A=1
2、 ABCD中∠A=60°,AB=6 AD=4.求平行四边形面积。
五.随堂练习
(1)sin60°-cos45°;(2)cos60°+tan60°;
六.小 结
我学会了什么?
七.作 业
1、P122 习题23.1 第1题
2、自选作业。
板书设计:
锐角三角函数
1.
2.30°,45°,60°角的三角函数值列表如下:
三角函数
角α
sinα
cosα
tanα
30°
45°
1
60°
课后反思:
锐角三角函数(三)
教学设计
时间:2014年11月21日
班级:九(2)班
褚集初级中学 马骏
