第二十二章 二次函数测试卷(含答案)2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数测试卷(含答案)2023—2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 00:00:00 | ||
图片预览



文档简介
第二十二章达标测试卷 (满分:150分 考试时间:120分钟)
一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案填在题后对应的括号内.
1.下列函数表达式中,一定是二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.y=3x2-2x+1 D.y=x2+
2.要得到抛物线y=-3(x+2)2+1,可以将抛物线y=-3x2+2( )
A.先向右平移2个单位长度,再向上平移1个单位长度
B.先向右平移2个单位长度,再向下平移1个单位长度
C.先向左平移2个单位长度,再向上平移1个单位长度
D.先向左平移2个单位长度,再向下平移1个单位长度
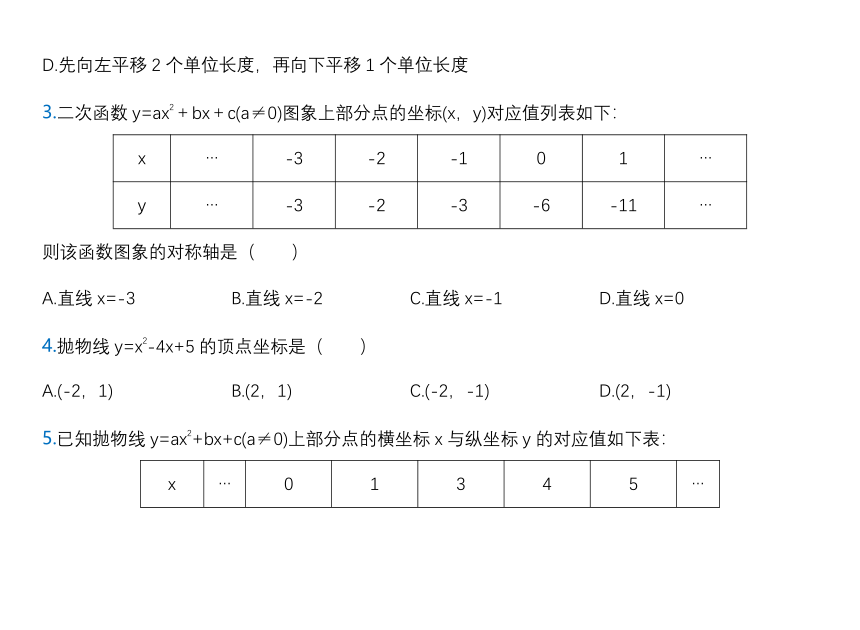
3.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … -3 -2 -1 0 1 …
y … -3 -2 -3 -6 -11 …
则该函数图象的对称轴是( )
A.直线x=-3 B.直线x=-2 C.直线x=-1 D.直线x=0
4.抛物线y=x2-4x+5的顶点坐标是( )
A.(-2,1) B.(2,1) C.(-2,-1) D.(2,-1)
5.已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x … 0 1 3 4 5 …
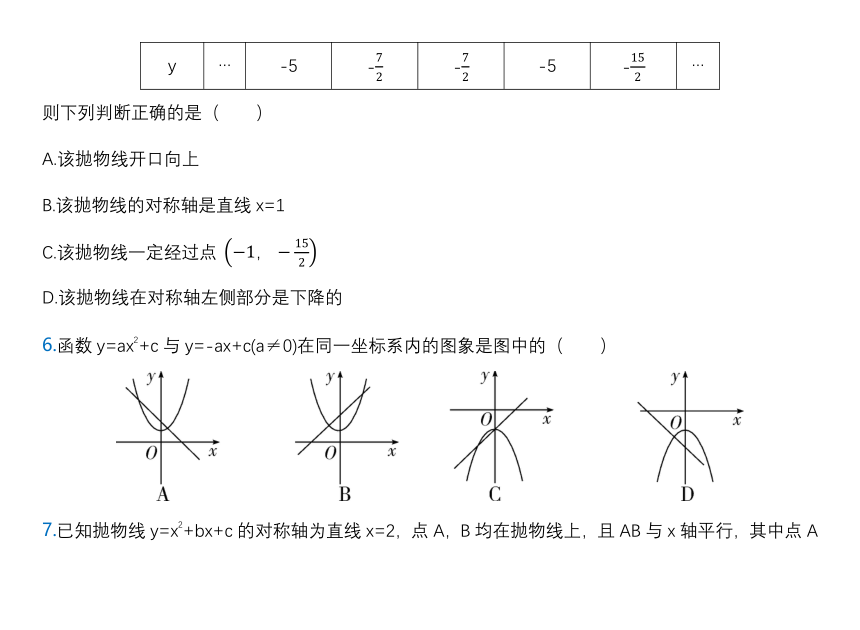
y … -5 - - -5 - …
则下列判断正确的是( )
A.该抛物线开口向上
B.该抛物线的对称轴是直线x=1
C.该抛物线一定经过点
D.该抛物线在对称轴左侧部分是下降的
6.函数y=ax2+c与y=-ax+c(a≠0)在同一坐标系内的图象是图中的( )
7.已知抛物线y=x2+bx+c的对称轴为直线x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2) C.(3,3) D.(4,3)
8.已知二次函数y=(x+m)2-1,当x≥-1时,y随x的增大而增大,则m的取值范围是( )
A.m=1 B.m≤1 C.m>1 D.m≥1
9.将二次函数y=2x2-4x+1的右边进行配方,正确的结果是( )
A.y=2(x-1)2+1 B.y=2(x+1)2-1
C.y=2(x-1)2-1 D.y=2(x+1)2+1
10.已知点A(-3,y1),B(0,y2),C(3,y3)是二次函数y=-(x+2)2+m图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1=y3<y2
C.y3<y2<y1 D.y1<y3<y2
11.若关于x的二次函数y=-x2+(2a-12)x+1,当x>-1时,y随x的增大而减小,且关于y的分式方程+=2的解是正整数,则所有满足条件的整数a的值之和是( )
A.5 B.8 C.12 D.15
12.如图是抛物线y=ax2+bx+c(a≠0)的图象,其对称轴为x=-1,且该图象与x轴的一个交点在点(-3,0)和
(-4,0)之间,并经过点(-2.3,y1)与点(1.5,y2),则下列结论:①abc>0;②3a+c>0;③y1<y2;④对于任意实数m,都有am2-bm<a-b(m≠1).其中正确结论的序号是( )
A.①②③ B.①③④
C.②③④ D.①②④
二、填空题(本大题4个小题,每小题4分,共16分)请将答案填在题后横线上.
13.某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是 .
14.已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为 .
15.广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离x(米)的函数解析式是y=-x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是 .
16.二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是 .
三、解答题(本大题9个小题,17、18每小题8分,19-25每小题10分,共86分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形.
17.已知二次函数y=ax2+4x+2的图象经过点A(3,-4).
(1)求a的值;
(2)求此抛物线的对称轴;
(3)直接写出函数y随自变量的增大而减小的x的取值范围.
18.已知二次函数y=x2-4x+c的图象经过点(3,0).
(1)求该二次函数的表达式;
(2)点P(4,n)向上平移2个单位得到点P′,若点P′落在该二次函数图象上,求n的值.
19.如图,在ABCD中,已知∠A=60°,BC=8,AB=6.P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连接CE,CP.
(1)若AP=3时,试求出△PEC的PE边上的高.
(2)当AP的长为多少时,△CPE的面积最大?并求出面积的最大值.
20.在关于x,y的二元一次方程组中.
(1)若a=3,求方程组的解;
(2)若S=a(3x+y),当a为何值时,S有最值?
21.如图,用长为6 m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计).
(1)求出y与x的函数关系式.
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
22.如图,抛物线y=ax2+bx+与直线AB交于点A(-1,0),B ,点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.
(1)求抛物线的解析式;
(2)设△ADB的面为S,求出当S取最大值时的点D的坐标.
23.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(单位:千克)与每千克售价x(单位:元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 45 50 60
销售量y(千克) 110 100 80
(1)求y与x之间的函数表达式.
(2)设商品每天的总利润为w(单位:元),则当每千克售价x定为多少元时,超市每天能获得的利润最大?最大利润是多少元?
24.如图,抛物线C1的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点.
(1)求抛物线C1的解析式.
(2)将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,点E为抛物线C3的顶点,在抛物线C2的对称轴上是否存在点F,使得△BEF为等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
25.如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(3,0)两点,与y轴交于C(0,-3),过点E(0,-1)的直线与抛物线交于A,D两点,点P是直线AD下方抛物线上一点(不与A,D重合).
(1)求抛物线的解析式与直线AD的解析式.
(2)如图①,过点P作PN∥y轴且交直线AD于点N,求线段PN的最大值.
(3)如图②,连接AP,DP,是否存在点P,使得△APD的面积等于3 若存在,求出此时点P的坐标;若不存在,请说明理由.
1.C
2.D
3.B
4.B
5.C
6.C
7.D
8.D
9.C
10.C
11.A
12.D
13. y=10(1+x)2
14.
15. 2米
16. -5<t≤4
17.解:(1)∵二次函数y=ax2+4x+2的图象经过点A(3,-4),
∴-4=9a+12+2,
解得a=-2,
∴a的值为-2.
(2)由(1)可知抛物线解析式为y=-2x2+4x+2=-2(x-1)2+4,
∴抛物线对称轴为直线x=1.
(3)∵抛物线开口向下,对称轴为x=1,
∴当x≥1时,y随x的增大而减小.
18.解:(1)把点(3,0)代入y=x2-4x+c得9-12+c=0,
解得c=3,
所以该二次函数的解析式为y=x2-4x+3.
(2)点P(4,n)向上平移2个单位得到点P′(4,n+2),
把点P′代入y=x2-4x+3中可得n+2=16-16+3,
解得n=1.
19.解:(1)如答图 ①,过点C作CH⊥AD于点H,
∵四边形ABCD是平行四边形,
∴AB=CD=6,BC=AD=8,AB∥CD,
∴∠CDH=∠A=60°.
∵CH⊥AD,∴∠DCH=30°,
∴DH=CD=3,CH=DH=3,
∴SABCD=8×3=24.
∵AP=3=PB,∴S△PBC=SABCD=6.
∵∠A=60°,PE⊥AB,∴∠AEP=30°,
∴AE=2AP=6,PE=3,
∴S△APE=×3×3.
∵DE=AD-AE=2,
∴S△CDE=×DE×CH=×2×3=3,
∴S△PEC=24-6--3,
∴PE边上的高==7.
(2)如答图②,延长PE交CD的延长线于点F,
设AP=x,△CPE的面积为y,
∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=8.
∵Rt△APE,∠A=60°,
∴∠PEA=30°,
∴AE=2x,PE=x.
在Rt△DEF中,∠DEF=∠PEA=30°,DE=AD-AE=8-2x,
∴DF=DE=4-x.
∵AB∥CD,PF⊥AB,∴PF⊥CD,
∴S△CPE=PE·CF,
即y=×x×(10-x)=-x2+5x,
配方得y=-(x-5)2+(0≤x≤4),
当x=4时,y有最大值为12,
即AP的长为4时,△CPE的面积最大,最大面积是12.
20.解:(1)当a=3时,方程组为
②×2,得4x-2y=2③,①+③,得5x=5,解得x=1,
把x=1代入①,得1+2y=3,解得y=1,∴方程组的解是
(2)方程组的两个方程相加,得3x+y=a+1,
∴S=a(3x+y)=a(a+1)=a2+a,
∴当a=-=-时,S有最值.
21.解:(1)∵宽为x m,∴长为m,
∴y=x·=-x2+3x(0<x<2).
(2)由(1)可知:y和x是二次函数关系,a=-<0,
∴函数有最大值,当x=-=1时,y最大= m2.
答:窗框的长和宽分别为1.5 m和1 m时才能使得窗户的透光面积最大,此时的最大面积为1.5 m2.
22.解:(1)∵抛物线y=ax2+bx+经过点A(-1,0),B ,
∴解得
∴抛物线的解析式为y=-x2+2x+.
(2)设点D坐标为 ,如答图,作直线DC⊥x轴,与AB交于点C,
∵直线AB的解析式为y=x+,
∴点C坐标为 .
∵S△ABD=S△ACD+S△BCD
= ×(4+1)
=-(m2-3m-4)
=- 2+,
∴当m=时,△ADB的面积最大,此时点D坐标为 .
23.解:(1)设y=kx+b,
将(50,100),(60,80)代入,得解得
∴y=-2x+200(40≤x≤60).
(2)w=(x-40)(-2x+200)=-2x2+280x-8 000
=-2(x-70)2+1 800.
∵40≤x≤60,∴当x=60时,w取得最大值为1 600.
答:当每千克售价x定为60元时,超市每天能获得最大利润,最大利润是1 600元.
24.解:(1)设解析式为y=a(x-1)(x+3),将C(0,3)代入,得a=-1,
∴抛物线C1的解析式为y=-x2-2x+3.
(2)存在.
∵抛物线C1的解析式为y=-x2-2x+3,
∴抛物线C1的顶点为(-1,4).
∵将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,
∴抛物线C2的解析式为y=-(x-3)2+4,抛物线C3的解析式为y=(x-3)2-4.
∵点E为抛物线C3的顶点,∴点E(3,-4),
∴BE==2.
∵点F在抛物线C2的对称轴上,∴点F横坐标为3.
若BE=EF=2,则点F坐标为(3,-4+2)或(3,-4-2);
若BE=BF,则点F与点E关于x轴对称,∴点F(3,4);
若BF=EF,则22+(4-EF)2=BF2,
∴BF=EF=,∴点F .
综上所述,当点F为(3,-4+2)或(3,-4-2)或(3,4)或 时,使得△BEF为等腰三角形.
25.解:(1)把A(-1,0),B(3,0),C(0,-3)分别代入y=ax2+bx+c(a≠0)中,
得解得
∴抛物线的解析式为y=x2-2x-3.
设直线AD的解析式为y=kx+m,
把A(-1,0),E(0,-1)分别代入y=kx+m中,
得解得
∴直线AD的解析式为y=-x-1.
(2)联立方程组
解得或
∴D(2,-3),
∴直线AD下方抛物线的自变量x的取值范围是-1<x<2.
设P(x,x2-2x-3),则N(x,-x-1),
∴PN=(-x-1)-(x2-2x-3)=-x2+x+2=- 2+.
∵-1<0,
∴当x=时,PN有最大值.
(3)存在点P,使得△APD的面积等于3.理由如下:
由(2)可知PN=-x2+x+2,
∴S△APD=S△APN+S△DPN=PN(x+1)+PN(2-x)=PN×3=(-x2+x+2).
∵S△APD=3,∴(-x2+x+2)=3,
解得x=0,x=1,
∴P(0,-3)或P(1,-4).
一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案填在题后对应的括号内.
1.下列函数表达式中,一定是二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.y=3x2-2x+1 D.y=x2+
2.要得到抛物线y=-3(x+2)2+1,可以将抛物线y=-3x2+2( )
A.先向右平移2个单位长度,再向上平移1个单位长度
B.先向右平移2个单位长度,再向下平移1个单位长度
C.先向左平移2个单位长度,再向上平移1个单位长度
D.先向左平移2个单位长度,再向下平移1个单位长度
3.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … -3 -2 -1 0 1 …
y … -3 -2 -3 -6 -11 …
则该函数图象的对称轴是( )
A.直线x=-3 B.直线x=-2 C.直线x=-1 D.直线x=0
4.抛物线y=x2-4x+5的顶点坐标是( )
A.(-2,1) B.(2,1) C.(-2,-1) D.(2,-1)
5.已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x … 0 1 3 4 5 …
y … -5 - - -5 - …
则下列判断正确的是( )
A.该抛物线开口向上
B.该抛物线的对称轴是直线x=1
C.该抛物线一定经过点
D.该抛物线在对称轴左侧部分是下降的
6.函数y=ax2+c与y=-ax+c(a≠0)在同一坐标系内的图象是图中的( )
7.已知抛物线y=x2+bx+c的对称轴为直线x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2) C.(3,3) D.(4,3)
8.已知二次函数y=(x+m)2-1,当x≥-1时,y随x的增大而增大,则m的取值范围是( )
A.m=1 B.m≤1 C.m>1 D.m≥1
9.将二次函数y=2x2-4x+1的右边进行配方,正确的结果是( )
A.y=2(x-1)2+1 B.y=2(x+1)2-1
C.y=2(x-1)2-1 D.y=2(x+1)2+1
10.已知点A(-3,y1),B(0,y2),C(3,y3)是二次函数y=-(x+2)2+m图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1=y3<y2
C.y3<y2<y1 D.y1<y3<y2
11.若关于x的二次函数y=-x2+(2a-12)x+1,当x>-1时,y随x的增大而减小,且关于y的分式方程+=2的解是正整数,则所有满足条件的整数a的值之和是( )
A.5 B.8 C.12 D.15
12.如图是抛物线y=ax2+bx+c(a≠0)的图象,其对称轴为x=-1,且该图象与x轴的一个交点在点(-3,0)和
(-4,0)之间,并经过点(-2.3,y1)与点(1.5,y2),则下列结论:①abc>0;②3a+c>0;③y1<y2;④对于任意实数m,都有am2-bm<a-b(m≠1).其中正确结论的序号是( )
A.①②③ B.①③④
C.②③④ D.①②④
二、填空题(本大题4个小题,每小题4分,共16分)请将答案填在题后横线上.
13.某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是 .
14.已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为 .
15.广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离x(米)的函数解析式是y=-x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是 .
16.二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是 .
三、解答题(本大题9个小题,17、18每小题8分,19-25每小题10分,共86分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形.
17.已知二次函数y=ax2+4x+2的图象经过点A(3,-4).
(1)求a的值;
(2)求此抛物线的对称轴;
(3)直接写出函数y随自变量的增大而减小的x的取值范围.
18.已知二次函数y=x2-4x+c的图象经过点(3,0).
(1)求该二次函数的表达式;
(2)点P(4,n)向上平移2个单位得到点P′,若点P′落在该二次函数图象上,求n的值.
19.如图,在ABCD中,已知∠A=60°,BC=8,AB=6.P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连接CE,CP.
(1)若AP=3时,试求出△PEC的PE边上的高.
(2)当AP的长为多少时,△CPE的面积最大?并求出面积的最大值.
20.在关于x,y的二元一次方程组中.
(1)若a=3,求方程组的解;
(2)若S=a(3x+y),当a为何值时,S有最值?
21.如图,用长为6 m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计).
(1)求出y与x的函数关系式.
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
22.如图,抛物线y=ax2+bx+与直线AB交于点A(-1,0),B ,点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.
(1)求抛物线的解析式;
(2)设△ADB的面为S,求出当S取最大值时的点D的坐标.
23.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(单位:千克)与每千克售价x(单位:元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 45 50 60
销售量y(千克) 110 100 80
(1)求y与x之间的函数表达式.
(2)设商品每天的总利润为w(单位:元),则当每千克售价x定为多少元时,超市每天能获得的利润最大?最大利润是多少元?
24.如图,抛物线C1的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点.
(1)求抛物线C1的解析式.
(2)将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,点E为抛物线C3的顶点,在抛物线C2的对称轴上是否存在点F,使得△BEF为等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
25.如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(3,0)两点,与y轴交于C(0,-3),过点E(0,-1)的直线与抛物线交于A,D两点,点P是直线AD下方抛物线上一点(不与A,D重合).
(1)求抛物线的解析式与直线AD的解析式.
(2)如图①,过点P作PN∥y轴且交直线AD于点N,求线段PN的最大值.
(3)如图②,连接AP,DP,是否存在点P,使得△APD的面积等于3 若存在,求出此时点P的坐标;若不存在,请说明理由.
1.C
2.D
3.B
4.B
5.C
6.C
7.D
8.D
9.C
10.C
11.A
12.D
13. y=10(1+x)2
14.
15. 2米
16. -5<t≤4
17.解:(1)∵二次函数y=ax2+4x+2的图象经过点A(3,-4),
∴-4=9a+12+2,
解得a=-2,
∴a的值为-2.
(2)由(1)可知抛物线解析式为y=-2x2+4x+2=-2(x-1)2+4,
∴抛物线对称轴为直线x=1.
(3)∵抛物线开口向下,对称轴为x=1,
∴当x≥1时,y随x的增大而减小.
18.解:(1)把点(3,0)代入y=x2-4x+c得9-12+c=0,
解得c=3,
所以该二次函数的解析式为y=x2-4x+3.
(2)点P(4,n)向上平移2个单位得到点P′(4,n+2),
把点P′代入y=x2-4x+3中可得n+2=16-16+3,
解得n=1.
19.解:(1)如答图 ①,过点C作CH⊥AD于点H,
∵四边形ABCD是平行四边形,
∴AB=CD=6,BC=AD=8,AB∥CD,
∴∠CDH=∠A=60°.
∵CH⊥AD,∴∠DCH=30°,
∴DH=CD=3,CH=DH=3,
∴SABCD=8×3=24.
∵AP=3=PB,∴S△PBC=SABCD=6.
∵∠A=60°,PE⊥AB,∴∠AEP=30°,
∴AE=2AP=6,PE=3,
∴S△APE=×3×3.
∵DE=AD-AE=2,
∴S△CDE=×DE×CH=×2×3=3,
∴S△PEC=24-6--3,
∴PE边上的高==7.
(2)如答图②,延长PE交CD的延长线于点F,
设AP=x,△CPE的面积为y,
∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=8.
∵Rt△APE,∠A=60°,
∴∠PEA=30°,
∴AE=2x,PE=x.
在Rt△DEF中,∠DEF=∠PEA=30°,DE=AD-AE=8-2x,
∴DF=DE=4-x.
∵AB∥CD,PF⊥AB,∴PF⊥CD,
∴S△CPE=PE·CF,
即y=×x×(10-x)=-x2+5x,
配方得y=-(x-5)2+(0≤x≤4),
当x=4时,y有最大值为12,
即AP的长为4时,△CPE的面积最大,最大面积是12.
20.解:(1)当a=3时,方程组为
②×2,得4x-2y=2③,①+③,得5x=5,解得x=1,
把x=1代入①,得1+2y=3,解得y=1,∴方程组的解是
(2)方程组的两个方程相加,得3x+y=a+1,
∴S=a(3x+y)=a(a+1)=a2+a,
∴当a=-=-时,S有最值.
21.解:(1)∵宽为x m,∴长为m,
∴y=x·=-x2+3x(0<x<2).
(2)由(1)可知:y和x是二次函数关系,a=-<0,
∴函数有最大值,当x=-=1时,y最大= m2.
答:窗框的长和宽分别为1.5 m和1 m时才能使得窗户的透光面积最大,此时的最大面积为1.5 m2.
22.解:(1)∵抛物线y=ax2+bx+经过点A(-1,0),B ,
∴解得
∴抛物线的解析式为y=-x2+2x+.
(2)设点D坐标为 ,如答图,作直线DC⊥x轴,与AB交于点C,
∵直线AB的解析式为y=x+,
∴点C坐标为 .
∵S△ABD=S△ACD+S△BCD
= ×(4+1)
=-(m2-3m-4)
=- 2+,
∴当m=时,△ADB的面积最大,此时点D坐标为 .
23.解:(1)设y=kx+b,
将(50,100),(60,80)代入,得解得
∴y=-2x+200(40≤x≤60).
(2)w=(x-40)(-2x+200)=-2x2+280x-8 000
=-2(x-70)2+1 800.
∵40≤x≤60,∴当x=60时,w取得最大值为1 600.
答:当每千克售价x定为60元时,超市每天能获得最大利润,最大利润是1 600元.
24.解:(1)设解析式为y=a(x-1)(x+3),将C(0,3)代入,得a=-1,
∴抛物线C1的解析式为y=-x2-2x+3.
(2)存在.
∵抛物线C1的解析式为y=-x2-2x+3,
∴抛物线C1的顶点为(-1,4).
∵将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,
∴抛物线C2的解析式为y=-(x-3)2+4,抛物线C3的解析式为y=(x-3)2-4.
∵点E为抛物线C3的顶点,∴点E(3,-4),
∴BE==2.
∵点F在抛物线C2的对称轴上,∴点F横坐标为3.
若BE=EF=2,则点F坐标为(3,-4+2)或(3,-4-2);
若BE=BF,则点F与点E关于x轴对称,∴点F(3,4);
若BF=EF,则22+(4-EF)2=BF2,
∴BF=EF=,∴点F .
综上所述,当点F为(3,-4+2)或(3,-4-2)或(3,4)或 时,使得△BEF为等腰三角形.
25.解:(1)把A(-1,0),B(3,0),C(0,-3)分别代入y=ax2+bx+c(a≠0)中,
得解得
∴抛物线的解析式为y=x2-2x-3.
设直线AD的解析式为y=kx+m,
把A(-1,0),E(0,-1)分别代入y=kx+m中,
得解得
∴直线AD的解析式为y=-x-1.
(2)联立方程组
解得或
∴D(2,-3),
∴直线AD下方抛物线的自变量x的取值范围是-1<x<2.
设P(x,x2-2x-3),则N(x,-x-1),
∴PN=(-x-1)-(x2-2x-3)=-x2+x+2=- 2+.
∵-1<0,
∴当x=时,PN有最大值.
(3)存在点P,使得△APD的面积等于3.理由如下:
由(2)可知PN=-x2+x+2,
∴S△APD=S△APN+S△DPN=PN(x+1)+PN(2-x)=PN×3=(-x2+x+2).
∵S△APD=3,∴(-x2+x+2)=3,
解得x=0,x=1,
∴P(0,-3)或P(1,-4).
同课章节目录
