北京课改版数学七年级上册1.4有理数的加法 说课 课件(共38张PPT)
文档属性
| 名称 | 北京课改版数学七年级上册1.4有理数的加法 说课 课件(共38张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 10:56:54 | ||
图片预览










文档简介
(共38张PPT)
二、教学目标的确定
三、教学方式与手段的选择
四、教学过程的设计
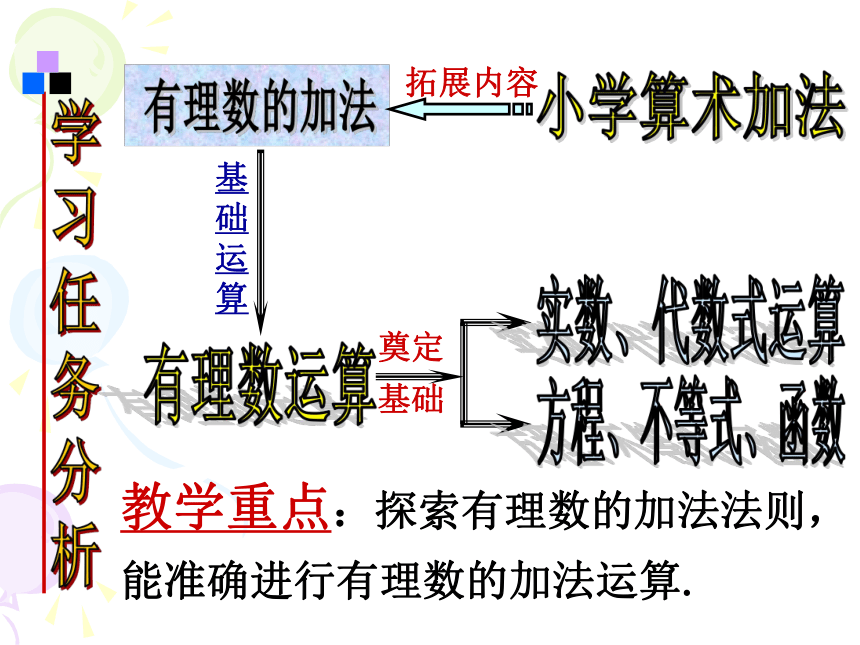
一、教学背景分析
基础运算
教学重点:探索有理数的加法法则,能准确进行有理数的加法运算.
拓展内容
奠定
基础
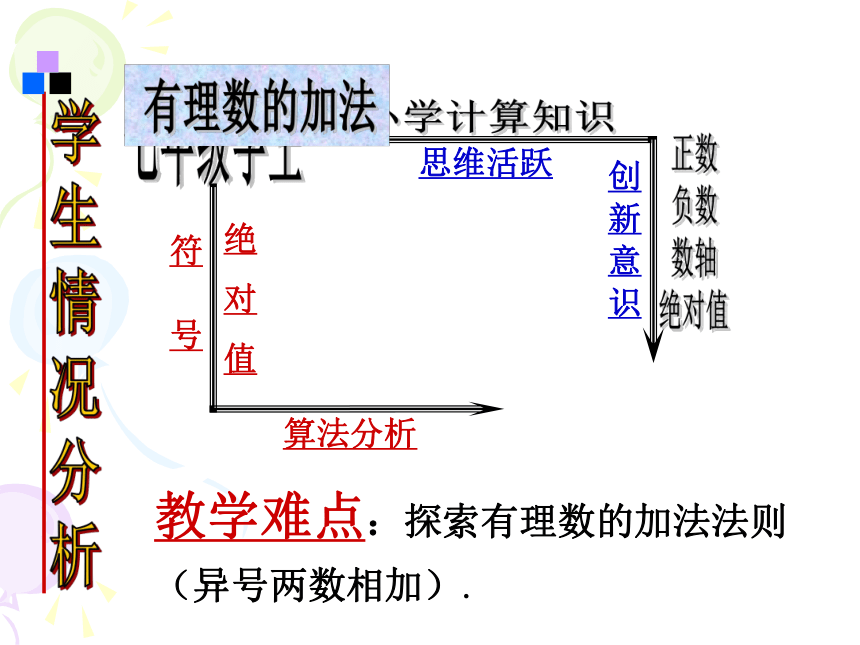
教学难点:探索有理数的加法法则(异号两数相加).
创
新
意
识
思维活跃
算法分析
符
号
绝
对
值
1.了解有理数加法的意义,掌握有理数的加法法则,能准确进行有理数的加法运算.
2.学生通过经历分类、探究、验证、归纳等活动,感受分类讨论的数学思想方法,体会由具体到抽象、由特殊到一般的认知规律,培养学生初步的创新意识和实践能力.
3.通过师生互动、合作交流,提高学生主动参与、乐于探究和与人合作的意识,增进学生学好数学的信心.
教学方式:
启发讲授
小组讨论
合作探究
教学手段:
科学计算器
几何画板
创设情境
引入新课
合作探究
学习新知
应用知识
培养能力
课堂小结
回顾知识
布置作业
巩固知识
通过举出与有理数加法有关的生活实例,使学生了解有理数加法的意义,理解学习有理数加法的必要性.
1.本阶段需要解决的主要问题
(一)创设情境,引入新课
(一)创设情境,引入新课
2.具体教学安排
问题1:你能用算式来表示这两个实际问题吗?
引例:在实际生活中,我们一般把收入记为正数,支出记为负数.
(1)某公司某天收入4万元,支出3万元,那么公司的这天总收入是多少万元?
(2)公司在另一天连续支出2万元和1万元,那么公司这天的总支出是多少万元?
问题2:你还能举出类似的生活实例吗?
(+4)+(-3)= +1
(-2)+(-1)= -3
(+4)+(-3)= +1
(-2)+(-1)= -3
(一)创设情境,引入新课
2.具体教学安排
(二)合作探究,学习新知
引导学生经历分类、验证、归纳等活动,探究有理数加法的运算法则,感受分类讨论的数学思想方法,体会由具体到抽象、由特殊到一般的认知规律.
1.本阶段需要解决的主要问题
2. 具体教学安排
提问:两个有理数相加,有哪些不同情况呢?
2. 具体教学安排
1
2
3
4
5
6
7
8
9
+
+
+
0
0
0
-
-
-
+
0
-
+
0
-
+
0
-
序号 一个加数 另一个加数
不同类型 一个加数 另一个加数
1 正数 正数
2 负数 负数
3 正数 负数
4 0 正数
5 0 0
6 0 负数
研究内容
0 + 负数负数+负数正数+负数
2. 具体教学安排
2. 具体教学安排
请同学们自由选取加数,列出四个不同的“0+负数”的算式,尽量选取不同形式的负有理数(整数、分数或小数),先猜想出结果,再利用计算器验证你的结果.
学生活动 :
1
猜想:0和一个负数相加,仍得这个负数.
提问:我们知道:0和一个正数相加,
仍得这个正数;0和0相加得0.
你能猜想出“0和一个负数相加”的结果吗?
小结:
0和任何一个有理数相加,仍得这个有理数.
2. 具体教学安排
问题1:你能举出一个生活实例来说明 “(-3)+(-4)”的结果吗?
(-3)+(-4)= -7
问题2: 我们知道“两个正数相加”的运算方法,你能猜想“两个负数相加”的运算方法吗?
引例:在实际生活中,我们一般把收入记为正数,支出记为负数.
(2)公司在另一天连续支出2万元和1万元,那么公司这天的总支出是多少万元?
(-2)+(-1)= -3
2. 具体教学安排
2
请同学们自由选取加数,列出四个不同的“ 0 + 负数 ”的算式,尽量选取不同形式的负有理数(整数、分数或小数),利用计算器计算出结果,验证你的猜想.
学生活动 :
负数+负数
序号 一个加数 另一个加数 算式 结果
1 ( )+( )=
2 ( )+( )=
3 ( )+( )=
4 ( )+( )=
(小组活动)
提问:
你能把“两个负数相加”
与“两个正数相加”的
运算方法统一起来吗?
和
符号
绝对值
同号两数相加
2. 具体教学安排
序号 一个加数 另一个加数 算式 结果
1 ( )+( )=
2 ( )+( )=
3 ( )+( )=
4 ( )+( )=
(小组活动)
3
请同学们自由选取加数,列出四个不同的“ 0 + 负数 ”的算式,尽量选取不同形式的有理数(整数、分数或小数),利用计算器计算出结果.
学生活动 :
负数+负数
正数+负数
符号
绝对值
异号两数相加
互为相反数的两个数的和为0.
思考:你能发现得到的结果与两个加数的符号及绝对值之间有什么关系?
(1)两个加数中,正数的绝对值较大;
(2)两个加数中,负数的绝对值较大;
和
(3)两个加数的绝对值相等.
对于其它有理数的加法运算,我们总结的运算方法是否适用呢?
2. 具体教学安排
0和一个有理数相加,仍得这个数.
和
符号
绝对值
异号两数相加
同号两数相加
互为相反数的两个数的和为0.
1.同号的两个数相加,符号不变,并把两个加数的绝对值相加.
2.异号的两个数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
互为相反数的两个数的和为0.
3.0和任何一个有理数相加,仍得这个有理数.
2. 具体教学安排
(三)应用知识,培养能力
以循序渐进的方法,使学生掌握有理数的加法法则,能准确进行有理数的加法运算;通过设置开放性的练习,培养学生的发散思维能力.
1.本阶段需要解决的主要问题
口算下列各题:
2.具体教学安排
(1)(-1)+(-5)= ;
(2)(+1)+(+6)= ;
(3)(+3)+(-7)= ;
(4)(-3)+(+7)= ;
(5)(-455)+ 0 = ;
(6)(- )+(+ )= .
-6
+7
-4
+4
-455
0
计算:
(1)(+26)+(+67);
(2)(-2.3)+(+7.8);
(3)(- )+(- );
(4)(+ )+(-1.375);
(5)(-0.673)+0;
(6) 0 +(+ ).
计算:
(2)(-2.3)+(+7.8)
= +(7.8 -2.3 )
= +5.5
(1)(+26)+(+67)
= +( 26+67)
= + 93
(同号两数相加)
(符号不变,并把两个加数的绝对值相加.)
(异号两数相加)
(取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.)
计算:
(1)(+26)+(+67);
(2)(-2.3)+(+7.8);
(3)(- )+(- );
(4)(+ )+(-1.375);
(5)(-0.673)+0;
(6) 0 +(+ ).
计算:
(1)(-12)+(-4.5)+(+10.7);
(2)(+ )+(+ )+(-5).
提问:你认为在有理数的加法运算中,应注意哪些问题?
“数字自选超市”里有11个有理数:
+8,+7,+5,+3,+2,
0,-2,-3,-5,-8,-13
请选择一对有理数填空,使得算式
|( )+( )|=5成立.
请同学们以小组为单位进行探究,看哪个小组得到的答案最多?
-5
-3
|( )+( )|=5
+8
+7
+5
+3
+2
0
-3
0
-8
-13
+8
|( )+( )|=5
(异号两数相加)
|( )+( )|=5
(同号两数相加)
-2
-2
|( )+( )|=5
(与0相加)
-5
-3
不同情况 ( )+( )= 5 ( )+( )=-5
①同号
两数相加 |(+2)+(+3)|=5 |(-2)+(-3)|=5
②异号
两数相加 |(+8)+(-3)|=5
|(+7)+(-2)|=5 |(-8)+(+3)|=5
|(-13)+(+8)|=5
③与零
相加 |(+5)+0|=5 |(-5)+0|=5
(四)课堂小结,回顾知识
本节课——
你学会了……
使你感触最深的是……
你感到最困难的是……
(1)进行有理数加法的运算时,要养成“先判断类型、再确定和的符号、最后计算和的绝对值”的运算习惯.
(2)“分类讨论”、“具体到抽象”、“特殊到一般”是我们研究数学问题常用的方法.
(五)布置作业,巩固知识
1.基础题:
(练习册)P50页 1、2
P51页 12、13
2.实践题:
分别在下图的圆圈内填上彼此都不相等的数,使得每条线上的三个数之和为零.你能得到多少种填法?
谢 谢!
二、教学目标的确定
三、教学方式与手段的选择
四、教学过程的设计
一、教学背景分析
基础运算
教学重点:探索有理数的加法法则,能准确进行有理数的加法运算.
拓展内容
奠定
基础
教学难点:探索有理数的加法法则(异号两数相加).
创
新
意
识
思维活跃
算法分析
符
号
绝
对
值
1.了解有理数加法的意义,掌握有理数的加法法则,能准确进行有理数的加法运算.
2.学生通过经历分类、探究、验证、归纳等活动,感受分类讨论的数学思想方法,体会由具体到抽象、由特殊到一般的认知规律,培养学生初步的创新意识和实践能力.
3.通过师生互动、合作交流,提高学生主动参与、乐于探究和与人合作的意识,增进学生学好数学的信心.
教学方式:
启发讲授
小组讨论
合作探究
教学手段:
科学计算器
几何画板
创设情境
引入新课
合作探究
学习新知
应用知识
培养能力
课堂小结
回顾知识
布置作业
巩固知识
通过举出与有理数加法有关的生活实例,使学生了解有理数加法的意义,理解学习有理数加法的必要性.
1.本阶段需要解决的主要问题
(一)创设情境,引入新课
(一)创设情境,引入新课
2.具体教学安排
问题1:你能用算式来表示这两个实际问题吗?
引例:在实际生活中,我们一般把收入记为正数,支出记为负数.
(1)某公司某天收入4万元,支出3万元,那么公司的这天总收入是多少万元?
(2)公司在另一天连续支出2万元和1万元,那么公司这天的总支出是多少万元?
问题2:你还能举出类似的生活实例吗?
(+4)+(-3)= +1
(-2)+(-1)= -3
(+4)+(-3)= +1
(-2)+(-1)= -3
(一)创设情境,引入新课
2.具体教学安排
(二)合作探究,学习新知
引导学生经历分类、验证、归纳等活动,探究有理数加法的运算法则,感受分类讨论的数学思想方法,体会由具体到抽象、由特殊到一般的认知规律.
1.本阶段需要解决的主要问题
2. 具体教学安排
提问:两个有理数相加,有哪些不同情况呢?
2. 具体教学安排
1
2
3
4
5
6
7
8
9
+
+
+
0
0
0
-
-
-
+
0
-
+
0
-
+
0
-
序号 一个加数 另一个加数
不同类型 一个加数 另一个加数
1 正数 正数
2 负数 负数
3 正数 负数
4 0 正数
5 0 0
6 0 负数
研究内容
0 + 负数负数+负数正数+负数
2. 具体教学安排
2. 具体教学安排
请同学们自由选取加数,列出四个不同的“0+负数”的算式,尽量选取不同形式的负有理数(整数、分数或小数),先猜想出结果,再利用计算器验证你的结果.
学生活动 :
1
猜想:0和一个负数相加,仍得这个负数.
提问:我们知道:0和一个正数相加,
仍得这个正数;0和0相加得0.
你能猜想出“0和一个负数相加”的结果吗?
小结:
0和任何一个有理数相加,仍得这个有理数.
2. 具体教学安排
问题1:你能举出一个生活实例来说明 “(-3)+(-4)”的结果吗?
(-3)+(-4)= -7
问题2: 我们知道“两个正数相加”的运算方法,你能猜想“两个负数相加”的运算方法吗?
引例:在实际生活中,我们一般把收入记为正数,支出记为负数.
(2)公司在另一天连续支出2万元和1万元,那么公司这天的总支出是多少万元?
(-2)+(-1)= -3
2. 具体教学安排
2
请同学们自由选取加数,列出四个不同的“ 0 + 负数 ”的算式,尽量选取不同形式的负有理数(整数、分数或小数),利用计算器计算出结果,验证你的猜想.
学生活动 :
负数+负数
序号 一个加数 另一个加数 算式 结果
1 ( )+( )=
2 ( )+( )=
3 ( )+( )=
4 ( )+( )=
(小组活动)
提问:
你能把“两个负数相加”
与“两个正数相加”的
运算方法统一起来吗?
和
符号
绝对值
同号两数相加
2. 具体教学安排
序号 一个加数 另一个加数 算式 结果
1 ( )+( )=
2 ( )+( )=
3 ( )+( )=
4 ( )+( )=
(小组活动)
3
请同学们自由选取加数,列出四个不同的“ 0 + 负数 ”的算式,尽量选取不同形式的有理数(整数、分数或小数),利用计算器计算出结果.
学生活动 :
负数+负数
正数+负数
符号
绝对值
异号两数相加
互为相反数的两个数的和为0.
思考:你能发现得到的结果与两个加数的符号及绝对值之间有什么关系?
(1)两个加数中,正数的绝对值较大;
(2)两个加数中,负数的绝对值较大;
和
(3)两个加数的绝对值相等.
对于其它有理数的加法运算,我们总结的运算方法是否适用呢?
2. 具体教学安排
0和一个有理数相加,仍得这个数.
和
符号
绝对值
异号两数相加
同号两数相加
互为相反数的两个数的和为0.
1.同号的两个数相加,符号不变,并把两个加数的绝对值相加.
2.异号的两个数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
互为相反数的两个数的和为0.
3.0和任何一个有理数相加,仍得这个有理数.
2. 具体教学安排
(三)应用知识,培养能力
以循序渐进的方法,使学生掌握有理数的加法法则,能准确进行有理数的加法运算;通过设置开放性的练习,培养学生的发散思维能力.
1.本阶段需要解决的主要问题
口算下列各题:
2.具体教学安排
(1)(-1)+(-5)= ;
(2)(+1)+(+6)= ;
(3)(+3)+(-7)= ;
(4)(-3)+(+7)= ;
(5)(-455)+ 0 = ;
(6)(- )+(+ )= .
-6
+7
-4
+4
-455
0
计算:
(1)(+26)+(+67);
(2)(-2.3)+(+7.8);
(3)(- )+(- );
(4)(+ )+(-1.375);
(5)(-0.673)+0;
(6) 0 +(+ ).
计算:
(2)(-2.3)+(+7.8)
= +(7.8 -2.3 )
= +5.5
(1)(+26)+(+67)
= +( 26+67)
= + 93
(同号两数相加)
(符号不变,并把两个加数的绝对值相加.)
(异号两数相加)
(取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.)
计算:
(1)(+26)+(+67);
(2)(-2.3)+(+7.8);
(3)(- )+(- );
(4)(+ )+(-1.375);
(5)(-0.673)+0;
(6) 0 +(+ ).
计算:
(1)(-12)+(-4.5)+(+10.7);
(2)(+ )+(+ )+(-5).
提问:你认为在有理数的加法运算中,应注意哪些问题?
“数字自选超市”里有11个有理数:
+8,+7,+5,+3,+2,
0,-2,-3,-5,-8,-13
请选择一对有理数填空,使得算式
|( )+( )|=5成立.
请同学们以小组为单位进行探究,看哪个小组得到的答案最多?
-5
-3
|( )+( )|=5
+8
+7
+5
+3
+2
0
-3
0
-8
-13
+8
|( )+( )|=5
(异号两数相加)
|( )+( )|=5
(同号两数相加)
-2
-2
|( )+( )|=5
(与0相加)
-5
-3
不同情况 ( )+( )= 5 ( )+( )=-5
①同号
两数相加 |(+2)+(+3)|=5 |(-2)+(-3)|=5
②异号
两数相加 |(+8)+(-3)|=5
|(+7)+(-2)|=5 |(-8)+(+3)|=5
|(-13)+(+8)|=5
③与零
相加 |(+5)+0|=5 |(-5)+0|=5
(四)课堂小结,回顾知识
本节课——
你学会了……
使你感触最深的是……
你感到最困难的是……
(1)进行有理数加法的运算时,要养成“先判断类型、再确定和的符号、最后计算和的绝对值”的运算习惯.
(2)“分类讨论”、“具体到抽象”、“特殊到一般”是我们研究数学问题常用的方法.
(五)布置作业,巩固知识
1.基础题:
(练习册)P50页 1、2
P51页 12、13
2.实践题:
分别在下图的圆圈内填上彼此都不相等的数,使得每条线上的三个数之和为零.你能得到多少种填法?
谢 谢!
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
