《探索图形》(课件)-五年级下册数学人教版(共23张PPT)
文档属性
| 名称 | 《探索图形》(课件)-五年级下册数学人教版(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 807.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 07:36:48 | ||
图片预览


文档简介
(共23张PPT)
探 索 图 形
——正方体的表面涂色问题
正方体有:
8个顶点;
6个完全一样的面。
12条长度相等的棱;
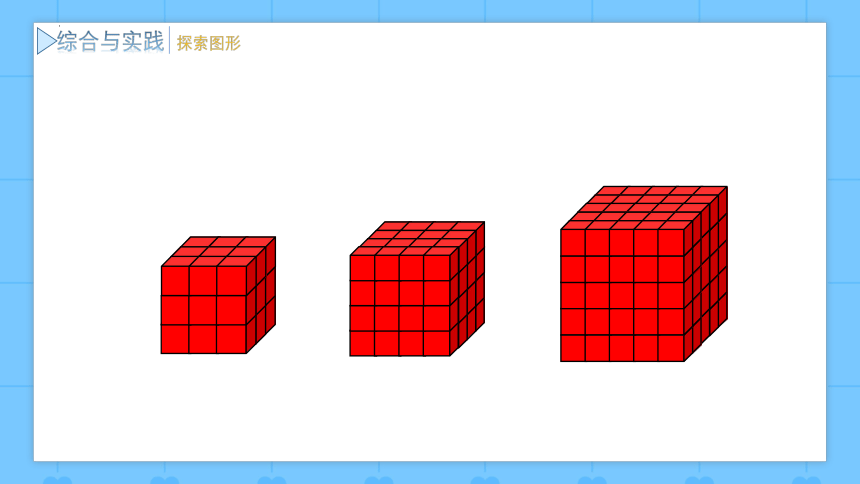
综合与实践
探索图形
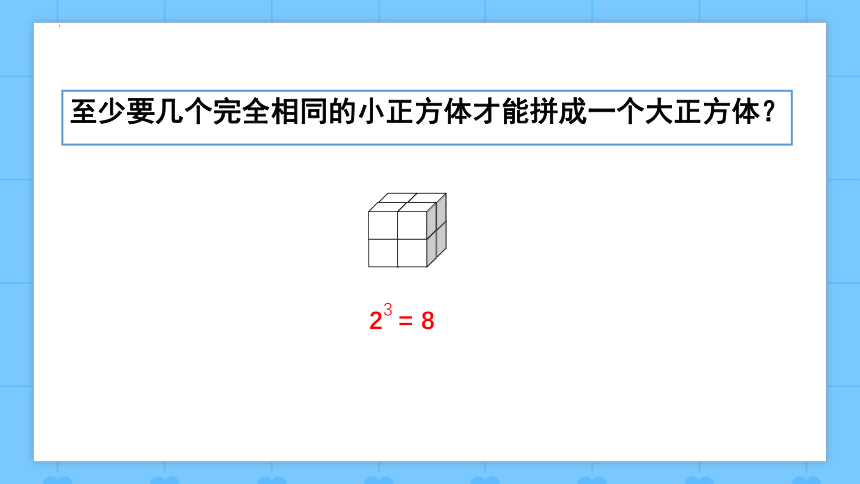
至少要几个完全相同的小正方体才能拼成一个大正方体?
2 = 8
3
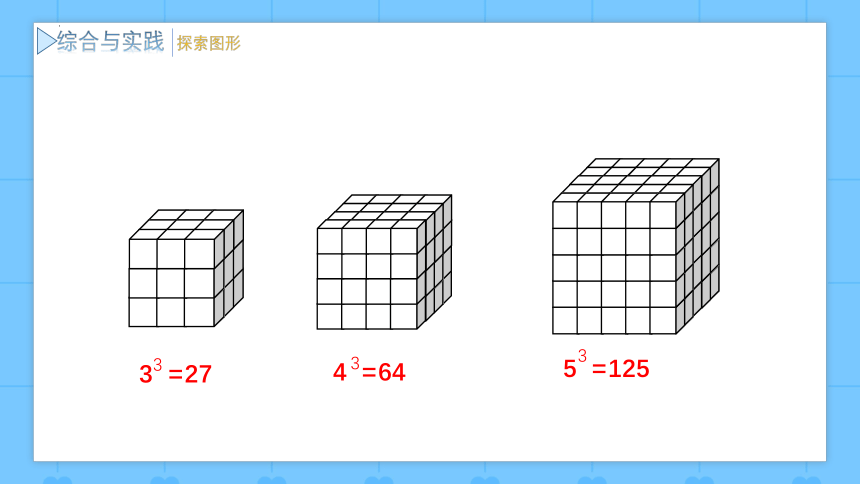
3 =27
4 =64
3
3
3
5 =125
综合与实践
探索图形
综合与实践
探索图形
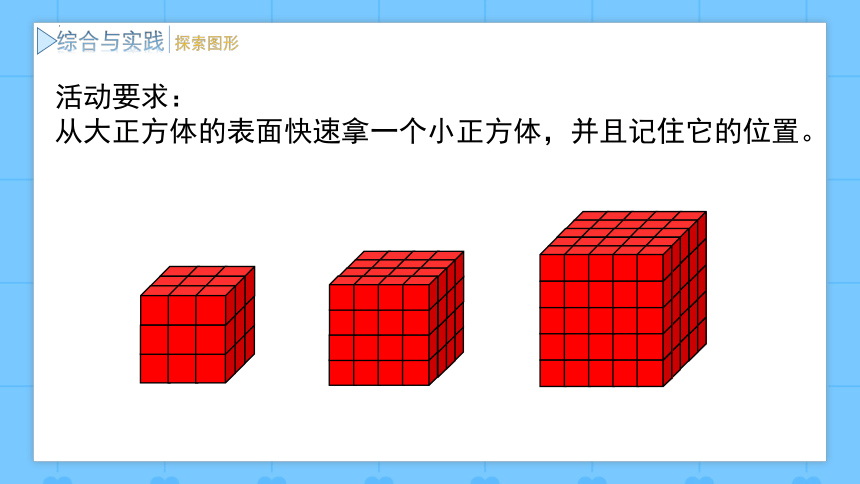
活动要求:
从大正方体的表面快速拿一个小正方体,并且记住它的位置。
综合与实践
探索图形
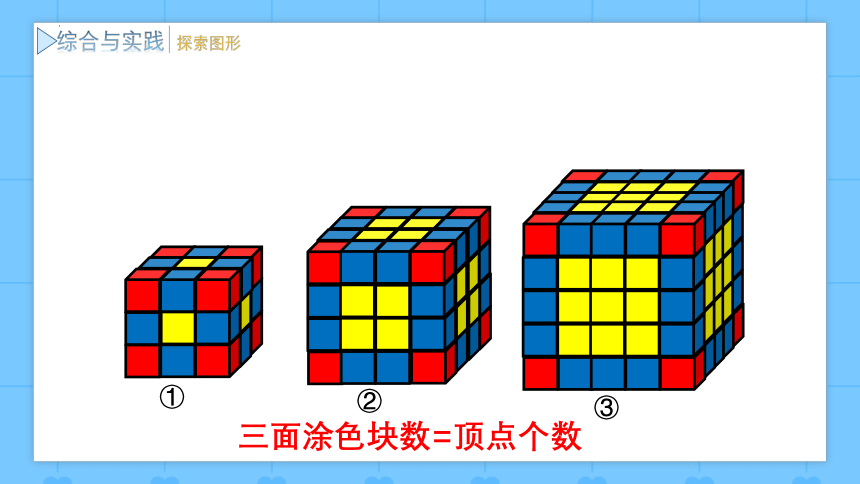
三面涂色块数=顶点个数
①
②
③
综合与实践
探索图形
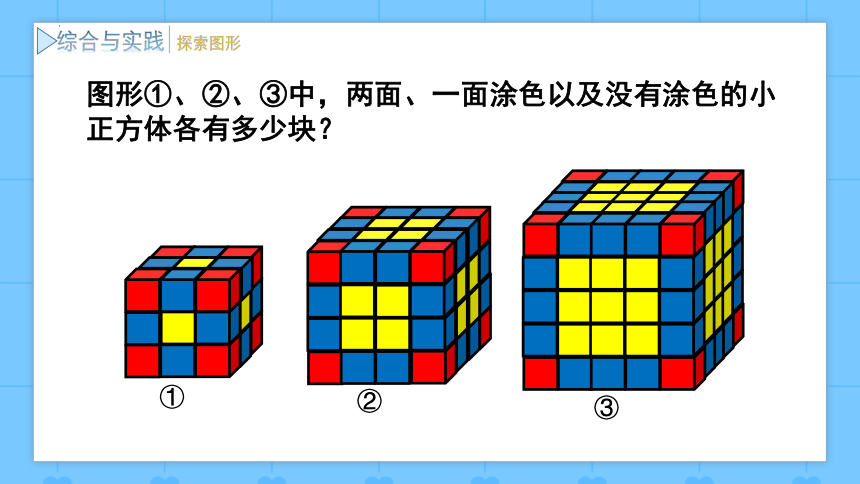
①
②
③
图形①、②、③中,两面、一面涂色以及没有涂色的小正方体各有多少块?
综合与实践
探索图形
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
3
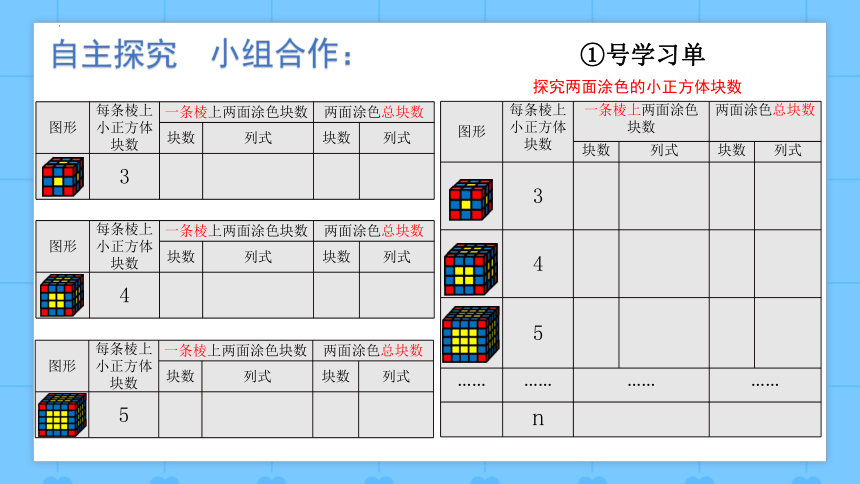
探究两面涂色的小正方体块数
自主探究 小组合作:
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
4
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
5
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
3
4
5
…… …… …… ……
n
①号学习单
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
3
探究一面涂色的小正方体块数
自主探究 小组合作:
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
4
图形 每条棱上小正方体块数 一面涂色总块数 一面涂色总块数
块数 列式 块数 列式
5
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
3
4
5
…… …… …… ……
n
②号学习单
两面涂色
的总块数=
(每条棱上块数-2)
×12
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
① 3
② 4
③ 5
…… …… …… ……
①号学习单
探究两面涂色的小正方体块数
①
②
③
1
3-2
12
(3-2)×12
2
4-2
24
(4-2)×12
3
5-2
36
(5-2)×12
n-2
(n-2)×12
6
4
6-2
48
(6-2)×12
n
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
① 3
② 4
③ 5
…… …… …… ……
n
②号学习单
探究一面涂色的小正方体块数
①
②
③
1
(3-2)
6
(3-2)×6
4
(4-2)
24
(4-2)×6
9
(5-2)
54
(5-2)×6
综合与实践
探索图形
(4-2)
(4-2)
×
=(4-2)
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
① 3
② 4
③ 5
…… …… …… ……
②号学习单
探究一面涂色的小正方体块数
①
②
③
1
(3-2)
6
(3-2)×6
4
(4-2)
24
(4-2)×6
9
(5-2)
54
(5-2)×6
(n-2)
(n-2) ×6
一面涂色
的总块数=
(每条棱上块数-2)
×6
6
16
(6-2)
96
(6-2)×6
2
n
4
2 =8
(4-2)
(4-2)
(4-2)
×
×
=(4-2)
5
综合与实践
探索图形
(5-2)
(5-2)
(5-2)
×
×
=(5-2)
图形 每条棱上块数 没有涂色块数
① 3
② 4
③ 5
…… …… ……
(5-2)=
3
(3-2) =
3
(n-2)
1
8
27
①
②
③
综合与实践
探索图形
没有涂色的块数=
(每条棱上块数-2)
3
3
(4-2) =
n
每条棱上小正方体块数 三面涂色块数 两面涂色 块数 一面涂色 块数 没有涂色
块数
3 8 12 6 1
4 8 24 24 8
5 8 36 54 27
…… …… …… …… ……
n 8 (n-2)×12 (n-2) ×6 (n-2)
综合与实践
探索图形
10
把表面涂色的正方体每条棱平均分成10份,从切成的小正方体中任取一个,会出现有颜色的和没有颜色的两种情况。
三面涂色
两面涂色
一面涂色
有颜色的
没有颜色的
没有涂色
男生
女生
有颜色的和没颜色的谁赢的可能性大?
方法一:
三面涂色:(10-2)=512(块)
总块数:10×10×10=1000(块)
有颜色的块数:1000-512=488(块)
512>488
答:选中没有颜色的获胜的可能性大。
方法二:
两面涂色:(10-2)×12=96(块)
一面涂色:(10-2)×6=384(块)
总块数:10×10×10=1000(块)
没有涂色块数:1000-8-96-384=512(块)
有颜色的块数:1000-512=488(块)
512>488
答:选中没有颜色的获胜的可能性大。
探究长方体中不同涂色情况的小正方体数量.
探 索 图 形
——正方体的表面涂色问题
正方体有:
8个顶点;
6个完全一样的面。
12条长度相等的棱;
综合与实践
探索图形
至少要几个完全相同的小正方体才能拼成一个大正方体?
2 = 8
3
3 =27
4 =64
3
3
3
5 =125
综合与实践
探索图形
综合与实践
探索图形
活动要求:
从大正方体的表面快速拿一个小正方体,并且记住它的位置。
综合与实践
探索图形
三面涂色块数=顶点个数
①
②
③
综合与实践
探索图形
①
②
③
图形①、②、③中,两面、一面涂色以及没有涂色的小正方体各有多少块?
综合与实践
探索图形
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
3
探究两面涂色的小正方体块数
自主探究 小组合作:
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
4
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
5
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
3
4
5
…… …… …… ……
n
①号学习单
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
3
探究一面涂色的小正方体块数
自主探究 小组合作:
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
4
图形 每条棱上小正方体块数 一面涂色总块数 一面涂色总块数
块数 列式 块数 列式
5
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
3
4
5
…… …… …… ……
n
②号学习单
两面涂色
的总块数=
(每条棱上块数-2)
×12
图形 每条棱上小正方体块数 一条棱上两面涂色块数 两面涂色总块数
块数 列式 块数 列式
① 3
② 4
③ 5
…… …… …… ……
①号学习单
探究两面涂色的小正方体块数
①
②
③
1
3-2
12
(3-2)×12
2
4-2
24
(4-2)×12
3
5-2
36
(5-2)×12
n-2
(n-2)×12
6
4
6-2
48
(6-2)×12
n
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
① 3
② 4
③ 5
…… …… …… ……
n
②号学习单
探究一面涂色的小正方体块数
①
②
③
1
(3-2)
6
(3-2)×6
4
(4-2)
24
(4-2)×6
9
(5-2)
54
(5-2)×6
综合与实践
探索图形
(4-2)
(4-2)
×
=(4-2)
图形 每条棱上小正方体块数 每个面上一面涂色块数 一面涂色总块数
块数 列式 块数 列式
① 3
② 4
③ 5
…… …… …… ……
②号学习单
探究一面涂色的小正方体块数
①
②
③
1
(3-2)
6
(3-2)×6
4
(4-2)
24
(4-2)×6
9
(5-2)
54
(5-2)×6
(n-2)
(n-2) ×6
一面涂色
的总块数=
(每条棱上块数-2)
×6
6
16
(6-2)
96
(6-2)×6
2
n
4
2 =8
(4-2)
(4-2)
(4-2)
×
×
=(4-2)
5
综合与实践
探索图形
(5-2)
(5-2)
(5-2)
×
×
=(5-2)
图形 每条棱上块数 没有涂色块数
① 3
② 4
③ 5
…… …… ……
(5-2)=
3
(3-2) =
3
(n-2)
1
8
27
①
②
③
综合与实践
探索图形
没有涂色的块数=
(每条棱上块数-2)
3
3
(4-2) =
n
每条棱上小正方体块数 三面涂色块数 两面涂色 块数 一面涂色 块数 没有涂色
块数
3 8 12 6 1
4 8 24 24 8
5 8 36 54 27
…… …… …… …… ……
n 8 (n-2)×12 (n-2) ×6 (n-2)
综合与实践
探索图形
10
把表面涂色的正方体每条棱平均分成10份,从切成的小正方体中任取一个,会出现有颜色的和没有颜色的两种情况。
三面涂色
两面涂色
一面涂色
有颜色的
没有颜色的
没有涂色
男生
女生
有颜色的和没颜色的谁赢的可能性大?
方法一:
三面涂色:(10-2)=512(块)
总块数:10×10×10=1000(块)
有颜色的块数:1000-512=488(块)
512>488
答:选中没有颜色的获胜的可能性大。
方法二:
两面涂色:(10-2)×12=96(块)
一面涂色:(10-2)×6=384(块)
总块数:10×10×10=1000(块)
没有涂色块数:1000-8-96-384=512(块)
有颜色的块数:1000-512=488(块)
512>488
答:选中没有颜色的获胜的可能性大。
探究长方体中不同涂色情况的小正方体数量.
