4.1.2 点、线、面、体 导学案(含答案)
文档属性
| 名称 | 4.1.2 点、线、面、体 导学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 355.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览

文档简介
1 几何图形
点、线、面、体导学案
学习目标
1.进一步认识立体图形与平面图形的关系,了解多面体可由平面图形围成.
2.通过展开与折叠,了解棱锥、棱柱、圆柱、长方体、正方体的表面展开图形.
3.根据展开图判断是否可以折叠成多面体.
学习过程
一、问题导学
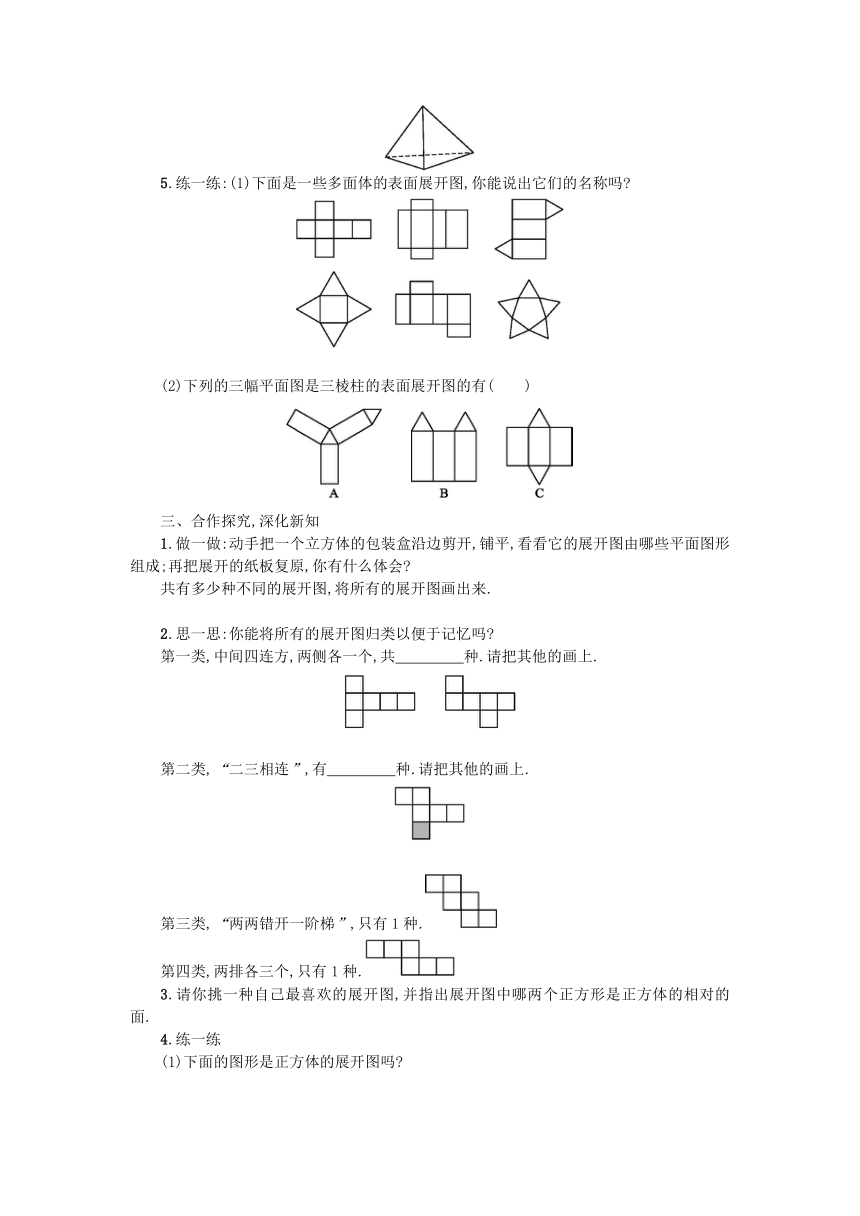
1.问题:(1)一面长方形的墙壁,壁虎在下方,蚊子在上方,饥饿的壁虎想尽快的吃掉上方的蚊子,走哪条路最近呢
(2)有一天壁虎在圆桶的下方,发现上方有一只蚊子,饥饿的它要想尽快吃到蚊子,走哪条路最近呢
壁虎是沿着圆柱的表面爬行的,它爬行的路线是任意的,但是哪一条是最短的路径,并不能直观地看出,于是我们尝试着把圆柱的表面展成平面图形来研究,这也就是我们本节课要讨论的立体图形的表面展开图.
二、动手实践,探索新知
1.你能说一说我们常见的立体图形吗
.
2.你能说一说圆柱、圆锥、长方体的展开图吗
在实际生活中常常需要了解整个立体图形展开的形状,如要制作一个长方体形状的纸盒,需要根据它的平面展开图来裁剪纸张,并不是同学们课前准备的那样用六张纸拼成的.
将立体图形的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的 .
3.做一做:12个一样大的等边三角形,粘贴成如下图所示的三种形状,你能想象哪一个可以折叠成多面体 动手做做看.
4.想一想:图(1)与图(3)是如何展开的,为什么产生这样不同的展开图呢
我们把图(1)与图(3)都叫做三棱锥的表面展开图.
5.练一练:(1)下面是一些多面体的表面展开图,你能说出它们的名称吗
(2)下列的三幅平面图是三棱柱的表面展开图的有( )
三、合作探究,深化新知
1.做一做:动手把一个立方体的包装盒沿边剪开,铺平,看看它的展开图由哪些平面图形组成;再把展开的纸板复原,你有什么体会
共有多少种不同的展开图,将所有的展开图画出来.
2.思一思:你能将所有的展开图归类以便于记忆吗
第一类,中间四连方,两侧各一个,共 种.请把其他的画上.
第二类,“二三相连”,有 种.请把其他的画上.
第三类,“两两错开一阶梯”,只有1种.
第四类,两排各三个,只有1种.
3.请你挑一种自己最喜欢的展开图,并指出展开图中哪两个正方形是正方体的相对的面.
4.练一练
(1)下面的图形是正方体的展开图吗
(2)下面是一个正方体的展开图,每个面中标着一个字,若折成正方体后,“坚”在下,“就”在后,你能判断“胜”“利”在正方体中的位置吗
(3)如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求a,b,c.
四、应用拓展
1.你知道其他棱柱的展开图吗 三棱柱、长方体、五棱柱……,球能展开成平面图形吗
2.(帮虫子出主意)有一只虫子在正方体的一个顶点A,要爬到距它最远的另一个顶点B去,有哪些路径 哪条路径最短
3.(回归第一环节)有一天壁虎在圆桶的下方,发现上方有一只蚊子,饥饿的它要想尽快吃到蚊子,走哪条路最近呢
五、小结反思
1.通过本节的学习活动,你了解了立体图形与平面图形的关系吗
2.你了解研究立体图形的方法吗
3.通过这节课学习,你制作正方体还会剪六张正方形吗 你会如何制作
六、布置作业
课本118页练习第2,3题,课本121页习题4.1第6,7题.
选做题:课本121页习题4.1第11,12题.
七、达标测试
1.下列图形是某些多面体的平面展开图,说出这些多面体的名称.
2.下列图形中,不是立方体表面展开图的是( )
3.有一个正方体,在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色.甲、乙、丙三位同学从三个不同的角度去观察此正方体,结果如下图,问这个正方体各个面的对面的颜色是什么
4.如图所示:
(1)如果将图中①~⑤的平面图形绕虚线旋转一周,可以得到Ⅰ~Ⅴ的几何体,请你把有对应关系的平面图形与几何体用线连接起来;
(2)在图Ⅰ~Ⅴ的几何体中,有顶点的几何体是 ,没有顶点的几何体是 ;
(3)图Ⅴ中的几何体由几个面围成?面与面相交形成几条线?它们是直的还是曲的?
参考答案
1.圆锥、五棱锥、六棱柱、圆柱、三棱锥、长方体、四棱锥、三棱柱、三棱柱、正方体;2.C;3.黄—黑,红—绿,白—蓝.
4.解:(1)如图所示.
(2)Ⅰ、Ⅱ、Ⅲ Ⅳ、Ⅴ
(3)Ⅴ中的几何体有2个面,其中一个是平面,一个是曲面,面与面相交有一条线,是一条曲线.
点、线、面、体导学案
学习目标
1.进一步认识立体图形与平面图形的关系,了解多面体可由平面图形围成.
2.通过展开与折叠,了解棱锥、棱柱、圆柱、长方体、正方体的表面展开图形.
3.根据展开图判断是否可以折叠成多面体.
学习过程
一、问题导学
1.问题:(1)一面长方形的墙壁,壁虎在下方,蚊子在上方,饥饿的壁虎想尽快的吃掉上方的蚊子,走哪条路最近呢
(2)有一天壁虎在圆桶的下方,发现上方有一只蚊子,饥饿的它要想尽快吃到蚊子,走哪条路最近呢
壁虎是沿着圆柱的表面爬行的,它爬行的路线是任意的,但是哪一条是最短的路径,并不能直观地看出,于是我们尝试着把圆柱的表面展成平面图形来研究,这也就是我们本节课要讨论的立体图形的表面展开图.
二、动手实践,探索新知
1.你能说一说我们常见的立体图形吗
.
2.你能说一说圆柱、圆锥、长方体的展开图吗
在实际生活中常常需要了解整个立体图形展开的形状,如要制作一个长方体形状的纸盒,需要根据它的平面展开图来裁剪纸张,并不是同学们课前准备的那样用六张纸拼成的.
将立体图形的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的 .
3.做一做:12个一样大的等边三角形,粘贴成如下图所示的三种形状,你能想象哪一个可以折叠成多面体 动手做做看.
4.想一想:图(1)与图(3)是如何展开的,为什么产生这样不同的展开图呢
我们把图(1)与图(3)都叫做三棱锥的表面展开图.
5.练一练:(1)下面是一些多面体的表面展开图,你能说出它们的名称吗
(2)下列的三幅平面图是三棱柱的表面展开图的有( )
三、合作探究,深化新知
1.做一做:动手把一个立方体的包装盒沿边剪开,铺平,看看它的展开图由哪些平面图形组成;再把展开的纸板复原,你有什么体会
共有多少种不同的展开图,将所有的展开图画出来.
2.思一思:你能将所有的展开图归类以便于记忆吗
第一类,中间四连方,两侧各一个,共 种.请把其他的画上.
第二类,“二三相连”,有 种.请把其他的画上.
第三类,“两两错开一阶梯”,只有1种.
第四类,两排各三个,只有1种.
3.请你挑一种自己最喜欢的展开图,并指出展开图中哪两个正方形是正方体的相对的面.
4.练一练
(1)下面的图形是正方体的展开图吗
(2)下面是一个正方体的展开图,每个面中标着一个字,若折成正方体后,“坚”在下,“就”在后,你能判断“胜”“利”在正方体中的位置吗
(3)如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求a,b,c.
四、应用拓展
1.你知道其他棱柱的展开图吗 三棱柱、长方体、五棱柱……,球能展开成平面图形吗
2.(帮虫子出主意)有一只虫子在正方体的一个顶点A,要爬到距它最远的另一个顶点B去,有哪些路径 哪条路径最短
3.(回归第一环节)有一天壁虎在圆桶的下方,发现上方有一只蚊子,饥饿的它要想尽快吃到蚊子,走哪条路最近呢
五、小结反思
1.通过本节的学习活动,你了解了立体图形与平面图形的关系吗
2.你了解研究立体图形的方法吗
3.通过这节课学习,你制作正方体还会剪六张正方形吗 你会如何制作
六、布置作业
课本118页练习第2,3题,课本121页习题4.1第6,7题.
选做题:课本121页习题4.1第11,12题.
七、达标测试
1.下列图形是某些多面体的平面展开图,说出这些多面体的名称.
2.下列图形中,不是立方体表面展开图的是( )
3.有一个正方体,在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色.甲、乙、丙三位同学从三个不同的角度去观察此正方体,结果如下图,问这个正方体各个面的对面的颜色是什么
4.如图所示:
(1)如果将图中①~⑤的平面图形绕虚线旋转一周,可以得到Ⅰ~Ⅴ的几何体,请你把有对应关系的平面图形与几何体用线连接起来;
(2)在图Ⅰ~Ⅴ的几何体中,有顶点的几何体是 ,没有顶点的几何体是 ;
(3)图Ⅴ中的几何体由几个面围成?面与面相交形成几条线?它们是直的还是曲的?
参考答案
1.圆锥、五棱锥、六棱柱、圆柱、三棱锥、长方体、四棱锥、三棱柱、三棱柱、正方体;2.C;3.黄—黑,红—绿,白—蓝.
4.解:(1)如图所示.
(2)Ⅰ、Ⅱ、Ⅲ Ⅳ、Ⅴ
(3)Ⅴ中的几何体有2个面,其中一个是平面,一个是曲面,面与面相交有一条线,是一条曲线.
