第四章 图形的平移与旋转单元测试题(含解析)
文档属性
| 名称 | 第四章 图形的平移与旋转单元测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 12:06:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
单元测试题
一、选择题(每小题5分,共30分)
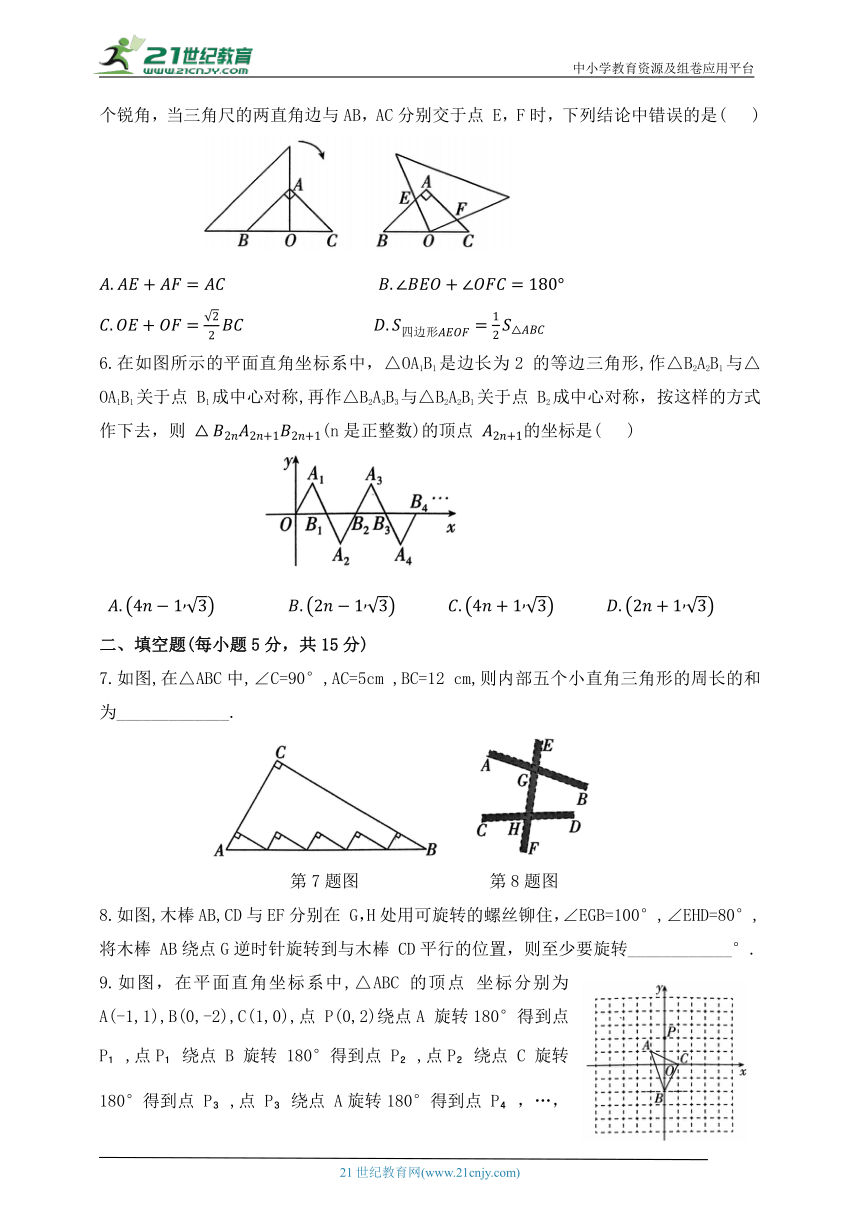
1.我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺. 比如下列图案分别表示“福”“禄”“寿”“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
2.如图,将△ABC先向右平移3个单位,再绕原点O 旋转 180°,得到△A'B'C',则点A 的对应点 A'的坐标是( )
A.(2,0) B.(-2,-3) C.(-1,-3) D.(-3,-1)
3.把一副三角板按如图所示的方法放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板 DEB绕点 B逆时针旋转45°得到△D'E'B,则点A 在△D'E'B的( )
A.内部 B.外部 C.边上 D.以上都有可能
第3题图 第4题图
4.如图,△ABC 是等腰直角三角形,BC 是斜边,P为△ABC内一点,将△ABP绕点A 逆时针旋转后,与 重合,如果AP=4,那么P,P'两点间的距离为( )
A.4 D.8
5.如图,在等腰直角三角形ABC中,∠BAC=90°,一个三角尺的直角顶点与BC边的中点 O 重合,且两条直角边分别经过点A 和点 B,将三角尺绕点 O 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点 E,F时,下列结论中错误的是( )
6.在如图所示的平面直角坐标系中,△OA1B1是边长为2 的等边三角形,作△B2A2B1与△OA1B1关于点 B1成中心对称,再作△B2A3B3与△B2A2B1关于点 B2成中心对称,按这样的方式作下去,则 (n是正整数)的顶点 的坐标是( )
二、填空题(每小题5分,共15分)
7.如图,在△ABC中,∠C=90°,AC=5cm ,BC=12 cm,则内部五个小直角三角形的周长的和为_____________.
第7题图 第8题图
8.如图,木棒AB,CD与EF分别在 G,H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒 AB绕点G逆时针旋转到与木棒 CD平行的位置,则至少要旋转____________°.
9.如图,在平面直角坐标系中,△ABC 的顶点 坐标分别为 A(-1,1),B(0,-2),C(1,0),点 P(0,2)绕点A 旋转180°得到点 P ,点P 绕点 B 旋转 180°得到点 P ,点P 绕点 C 旋转 180°得到点 P ,点 P 绕点 A旋转180°得到点 P ,…,按此作法进行下去,则点P 的坐标为____________.
三、解答题(共55分)
10.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC三个顶点的坐标分别为A(-1,1),B(-4,2),C(-3,4).
(1)请画出△ABC绕着原点 O 顺时针旋转90°的△A B C .
(2)请写出点 A ,B ,C 的坐标,观察对应点之间的坐标特征,若点 P(a,b)在△ABC上,写出点P的对应点 P 的坐标.
(3)若△A B C 与△ABC 关于原点 O 成中心对称,写出点A 的对应点 A 的坐标.
11.如图,在 Rt△ABC中,∠ACB=90°.线段 EF是由线段 AB平移得到的,点F在边 BC上,△EFD是以 EF为斜边的等腰直角三角形,且点D恰好在 AC 的延长线上.
(1)求证:∠ADE=∠DFC;
(2)求证:CD=BF.
12.【问题提出】
如图(1),已知△ABC是等边三角形,点E 在线段AB上,点 D在直线 BC上,且 ED=EC,将△BCE绕点 C 顺时针旋转60°至△ACF,连接EF.
试证明:AB=DB+AF.
【类比探究】
(1)如图(2),如果点E在线段 AB 的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系 请说明理由.
(2)如果点E在线段 BA 的延长线上,其他条件不变,请在图(3)的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
参考答案
1. D【解析】①不是中心对称图形,②是中心对称图形,③不是中心对称图形,④是中心对称图形. 故符合题意的是②④.故选 D.
2. C【解析】由题图可知,点A的坐标为(-2,3),将△ABC先向右平移3个单位,得点A平移后的坐标为(1,3),再绕原点 O 旋转 180°,得到△A'B'C',则点A 的对应点 A'的坐标是(-1,-3).故选C.
3. C【解析】∵AC=BD=10,∠ABC=∠DEB=90°,∠A=45°,∠D=30°,∴ BE=5,AB=BC=由三角板 DEB绕点 B逆时针旋转45°得到△D'E'B,设△D'E'B与直线 AB 交于点G,可知 ∴△GE'B是等腰直角三角形,且 又 ∴BG=AB,即点G与点 A 重合,∴点 A 在△D'E'B的边上.故选C.
4. B【解析】连接PP'.∵△ABP绕点A逆时针旋转后与△ACP'重合,∴△ABP≌△ACP',
∴∠BAP=∠CAP',∴∠BAP+∠PAC=∠CAP'+∠PAC,即
又∵AP=故选B.
5. C【解析】连接AO,如图所示.∵△ABC为等腰直角三角形,点O 为BC 的中点,
∴OA= OC,∠AOC = 90°,∠BAO=∠ACO = 45°. ∵∠EOA +∠AOF=∠EOF= 90°,∠AOF+∠FOC= ∠AOC = 90°,∴∠EOA=∠FOC,∴△EOA≌△FOC(ASA),∴EA=FC,∴AE+AF=AF+FC=AC,选项A正确.∵∠BEO+∠AEO=180°,∠AEO=∠OFC,∴∠BEO+ ∠OFC=180°,选项B 正确.作OM⊥AB交 AB于M点,ON⊥AC 交 AC 于 N点.∵∠BMO= ∠ONC=90°,∠B=∠C=45°,∴OM= 在△OEM和△ONF中,OE+OF>OM+只有当E,F分别与M,N重合时,即三角尺绕点 O顺时针旋转45°时,才有 选项C错误.∵△EOA≌△选项D正确.故选C.
6. C【解析】∵△OA B 是边长为2的等边三角形,∴点A 的坐标为( 的坐标为(2,0).∵△B A B 与△OA B 关于点B 成中心对称,∴点A 与点 A 关于点B 成中心对称. 点A 的坐标是( 的坐标是(4,0).∵△B A B 与△B A B 关于点 B 成中心对称,∴点A 与点A 关于点B 成中心对称. 点A 的坐标是 的坐标是(6,0).∵△B A B 与△B A B 关于点B 成中心对称,∴点A 与点A 关于点B 成中心对称.∵2×4-1=7, ∴点A 的坐标是 B 的坐标是(8,0).….∵1=2×1-1,3=2×2-1,5=2×3-1,7=2×4-1,…,∴点An的横坐标是2n-1,点A n+ 的横坐标是2(2n+1)-1=4n+1.∵当n为奇数时, An的纵坐标是 当n为偶数时, An的纵坐标是 顶点. 的纵坐标是 (n是正整数)的顶点 A n+1 的坐标是 故选C.
7.30cm【解析】∵在△ABC中,∠C=90°,AC=.由题图可以看出,内部小直角三角形的直角边是大直角三角形的直角边平移得到的,故内部五个小直角三角形的周长为 AC+BC+AB=30cm.故答案为30cm .
8.20【解析】如图,过点 G作 MN∥CD,则∠EGN=∠EHD= 80°. ∵∠EGB = 100°,
∴∠BGN=∠EGB-∠EGN= 100°-80°=20°.故至少要旋转20°.故答案为20.
9.(-2,0)【解析】如图所示,P (-2,0),P (2,-4),P (0,4),P (-2,-2),P (2,-2),
P (0,2),发现6次旋转为一个循环.因为所以点 的坐标与P 的坐标相同,即. 的坐标为(-2,0).
10.【解】(1)如图,△A B C 即为所求.
(2)A (1,1),B (2,4),C (4,3),点 P 的坐标为(b,-a).
(3)点A 的坐标为(1,-1).
11.【证明】(1)在等腰直角三角形EDF 中,∠EDF=90°,∴∠ADE+∠ADF=90°.
∵∠ACB=90°,∴∠DFC+∠ADF=90°,∴∠ADE=∠DFC.
(2)如图,连接AE.
∵线段 EF是由线段 AB平移得到的,∴AE∥BF,AE=BF,∴∠DAE=∠BCA=90°,
∴∠DAE=∠FCD=90°.
在△ADE 和△CFD中 ∴△ADE≌△CFD(AAS),
∴AE=CD.∵AE=BF,∴CD=BF.
12.【问题提出】【证明】由旋转知 BE = AF,∠ABC=∠FAC,EC=FC,∠ECF=60°,
∴△ECF是等边三角形,∴∠FEC=60°,∴∠AEF+∠BEC=120°.
∵△ABC是等边三角形,∴∠BAC=∠ABC=60°,∴∠BEC+∠BCE=120°,∴∠AEF=∠BCE.
∵ED=EC,∴∠D=∠ECD,∴∠AEF=∠D.∵∠FAC=60°,∠BAC=60°,∴∠EAF=120°.
∵∠ABC=60°,∴∠DBE=120°,∴∠EAF=∠DBE,∴△AEF≌△BDE,
∴AE=DB.∵AB=AE+EB,∴AB=DB+AF.
【类比探究】【解】(1)AB=DB-AF.理由:
由旋转知BE=AF,∠EBC=∠FAC,EC=FC,∠ECF=60°,∴△ECF是等边三角形,
∴∠FEC=60°,∴∠FEA+∠BEC=60°.
∵△ABC是等边三角形,∴∠BAC=∠ABC=60°,∴∠BEC+∠BCE=60°,∴∠FEA=∠BCE.
∵DE=CE,∴∠D=∠BCE,∴∠FEA=∠D.
∵∠ABC=60°,∴∠DBE=60°,∠EBC=120°,∴∠FAC=∠EBC=120°.
∵∠BAC=60°,∴∠FAE=60°,∴∠FAE=∠DBE.
∵∠FEA=∠D,AF=BE,∴△AEF≌△BDE,∴AE=DB.
∵AB=AE-BE,∴AB=DB-AF.
(2)如图. AB=AF-DB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 图形的平移与旋转
单元测试题
一、选择题(每小题5分,共30分)
1.我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺. 比如下列图案分别表示“福”“禄”“寿”“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
2.如图,将△ABC先向右平移3个单位,再绕原点O 旋转 180°,得到△A'B'C',则点A 的对应点 A'的坐标是( )
A.(2,0) B.(-2,-3) C.(-1,-3) D.(-3,-1)
3.把一副三角板按如图所示的方法放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板 DEB绕点 B逆时针旋转45°得到△D'E'B,则点A 在△D'E'B的( )
A.内部 B.外部 C.边上 D.以上都有可能
第3题图 第4题图
4.如图,△ABC 是等腰直角三角形,BC 是斜边,P为△ABC内一点,将△ABP绕点A 逆时针旋转后,与 重合,如果AP=4,那么P,P'两点间的距离为( )
A.4 D.8
5.如图,在等腰直角三角形ABC中,∠BAC=90°,一个三角尺的直角顶点与BC边的中点 O 重合,且两条直角边分别经过点A 和点 B,将三角尺绕点 O 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点 E,F时,下列结论中错误的是( )
6.在如图所示的平面直角坐标系中,△OA1B1是边长为2 的等边三角形,作△B2A2B1与△OA1B1关于点 B1成中心对称,再作△B2A3B3与△B2A2B1关于点 B2成中心对称,按这样的方式作下去,则 (n是正整数)的顶点 的坐标是( )
二、填空题(每小题5分,共15分)
7.如图,在△ABC中,∠C=90°,AC=5cm ,BC=12 cm,则内部五个小直角三角形的周长的和为_____________.
第7题图 第8题图
8.如图,木棒AB,CD与EF分别在 G,H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒 AB绕点G逆时针旋转到与木棒 CD平行的位置,则至少要旋转____________°.
9.如图,在平面直角坐标系中,△ABC 的顶点 坐标分别为 A(-1,1),B(0,-2),C(1,0),点 P(0,2)绕点A 旋转180°得到点 P ,点P 绕点 B 旋转 180°得到点 P ,点P 绕点 C 旋转 180°得到点 P ,点 P 绕点 A旋转180°得到点 P ,…,按此作法进行下去,则点P 的坐标为____________.
三、解答题(共55分)
10.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC三个顶点的坐标分别为A(-1,1),B(-4,2),C(-3,4).
(1)请画出△ABC绕着原点 O 顺时针旋转90°的△A B C .
(2)请写出点 A ,B ,C 的坐标,观察对应点之间的坐标特征,若点 P(a,b)在△ABC上,写出点P的对应点 P 的坐标.
(3)若△A B C 与△ABC 关于原点 O 成中心对称,写出点A 的对应点 A 的坐标.
11.如图,在 Rt△ABC中,∠ACB=90°.线段 EF是由线段 AB平移得到的,点F在边 BC上,△EFD是以 EF为斜边的等腰直角三角形,且点D恰好在 AC 的延长线上.
(1)求证:∠ADE=∠DFC;
(2)求证:CD=BF.
12.【问题提出】
如图(1),已知△ABC是等边三角形,点E 在线段AB上,点 D在直线 BC上,且 ED=EC,将△BCE绕点 C 顺时针旋转60°至△ACF,连接EF.
试证明:AB=DB+AF.
【类比探究】
(1)如图(2),如果点E在线段 AB 的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系 请说明理由.
(2)如果点E在线段 BA 的延长线上,其他条件不变,请在图(3)的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
参考答案
1. D【解析】①不是中心对称图形,②是中心对称图形,③不是中心对称图形,④是中心对称图形. 故符合题意的是②④.故选 D.
2. C【解析】由题图可知,点A的坐标为(-2,3),将△ABC先向右平移3个单位,得点A平移后的坐标为(1,3),再绕原点 O 旋转 180°,得到△A'B'C',则点A 的对应点 A'的坐标是(-1,-3).故选C.
3. C【解析】∵AC=BD=10,∠ABC=∠DEB=90°,∠A=45°,∠D=30°,∴ BE=5,AB=BC=由三角板 DEB绕点 B逆时针旋转45°得到△D'E'B,设△D'E'B与直线 AB 交于点G,可知 ∴△GE'B是等腰直角三角形,且 又 ∴BG=AB,即点G与点 A 重合,∴点 A 在△D'E'B的边上.故选C.
4. B【解析】连接PP'.∵△ABP绕点A逆时针旋转后与△ACP'重合,∴△ABP≌△ACP',
∴∠BAP=∠CAP',∴∠BAP+∠PAC=∠CAP'+∠PAC,即
又∵AP=故选B.
5. C【解析】连接AO,如图所示.∵△ABC为等腰直角三角形,点O 为BC 的中点,
∴OA= OC,∠AOC = 90°,∠BAO=∠ACO = 45°. ∵∠EOA +∠AOF=∠EOF= 90°,∠AOF+∠FOC= ∠AOC = 90°,∴∠EOA=∠FOC,∴△EOA≌△FOC(ASA),∴EA=FC,∴AE+AF=AF+FC=AC,选项A正确.∵∠BEO+∠AEO=180°,∠AEO=∠OFC,∴∠BEO+ ∠OFC=180°,选项B 正确.作OM⊥AB交 AB于M点,ON⊥AC 交 AC 于 N点.∵∠BMO= ∠ONC=90°,∠B=∠C=45°,∴OM= 在△OEM和△ONF中,OE+OF>OM+只有当E,F分别与M,N重合时,即三角尺绕点 O顺时针旋转45°时,才有 选项C错误.∵△EOA≌△选项D正确.故选C.
6. C【解析】∵△OA B 是边长为2的等边三角形,∴点A 的坐标为( 的坐标为(2,0).∵△B A B 与△OA B 关于点B 成中心对称,∴点A 与点 A 关于点B 成中心对称. 点A 的坐标是( 的坐标是(4,0).∵△B A B 与△B A B 关于点 B 成中心对称,∴点A 与点A 关于点B 成中心对称. 点A 的坐标是 的坐标是(6,0).∵△B A B 与△B A B 关于点B 成中心对称,∴点A 与点A 关于点B 成中心对称.∵2×4-1=7, ∴点A 的坐标是 B 的坐标是(8,0).….∵1=2×1-1,3=2×2-1,5=2×3-1,7=2×4-1,…,∴点An的横坐标是2n-1,点A n+ 的横坐标是2(2n+1)-1=4n+1.∵当n为奇数时, An的纵坐标是 当n为偶数时, An的纵坐标是 顶点. 的纵坐标是 (n是正整数)的顶点 A n+1 的坐标是 故选C.
7.30cm【解析】∵在△ABC中,∠C=90°,AC=.由题图可以看出,内部小直角三角形的直角边是大直角三角形的直角边平移得到的,故内部五个小直角三角形的周长为 AC+BC+AB=30cm.故答案为30cm .
8.20【解析】如图,过点 G作 MN∥CD,则∠EGN=∠EHD= 80°. ∵∠EGB = 100°,
∴∠BGN=∠EGB-∠EGN= 100°-80°=20°.故至少要旋转20°.故答案为20.
9.(-2,0)【解析】如图所示,P (-2,0),P (2,-4),P (0,4),P (-2,-2),P (2,-2),
P (0,2),发现6次旋转为一个循环.因为所以点 的坐标与P 的坐标相同,即. 的坐标为(-2,0).
10.【解】(1)如图,△A B C 即为所求.
(2)A (1,1),B (2,4),C (4,3),点 P 的坐标为(b,-a).
(3)点A 的坐标为(1,-1).
11.【证明】(1)在等腰直角三角形EDF 中,∠EDF=90°,∴∠ADE+∠ADF=90°.
∵∠ACB=90°,∴∠DFC+∠ADF=90°,∴∠ADE=∠DFC.
(2)如图,连接AE.
∵线段 EF是由线段 AB平移得到的,∴AE∥BF,AE=BF,∴∠DAE=∠BCA=90°,
∴∠DAE=∠FCD=90°.
在△ADE 和△CFD中 ∴△ADE≌△CFD(AAS),
∴AE=CD.∵AE=BF,∴CD=BF.
12.【问题提出】【证明】由旋转知 BE = AF,∠ABC=∠FAC,EC=FC,∠ECF=60°,
∴△ECF是等边三角形,∴∠FEC=60°,∴∠AEF+∠BEC=120°.
∵△ABC是等边三角形,∴∠BAC=∠ABC=60°,∴∠BEC+∠BCE=120°,∴∠AEF=∠BCE.
∵ED=EC,∴∠D=∠ECD,∴∠AEF=∠D.∵∠FAC=60°,∠BAC=60°,∴∠EAF=120°.
∵∠ABC=60°,∴∠DBE=120°,∴∠EAF=∠DBE,∴△AEF≌△BDE,
∴AE=DB.∵AB=AE+EB,∴AB=DB+AF.
【类比探究】【解】(1)AB=DB-AF.理由:
由旋转知BE=AF,∠EBC=∠FAC,EC=FC,∠ECF=60°,∴△ECF是等边三角形,
∴∠FEC=60°,∴∠FEA+∠BEC=60°.
∵△ABC是等边三角形,∴∠BAC=∠ABC=60°,∴∠BEC+∠BCE=60°,∴∠FEA=∠BCE.
∵DE=CE,∴∠D=∠BCE,∴∠FEA=∠D.
∵∠ABC=60°,∴∠DBE=60°,∠EBC=120°,∴∠FAC=∠EBC=120°.
∵∠BAC=60°,∴∠FAE=60°,∴∠FAE=∠DBE.
∵∠FEA=∠D,AF=BE,∴△AEF≌△BDE,∴AE=DB.
∵AB=AE-BE,∴AB=DB-AF.
(2)如图. AB=AF-DB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
