4.3 中心对称同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
3 中心对称
刷基础
知识点1 中心对称的定义及性质
1.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2.在平面直角坐标系中,点A(a,1)与点 B(-2,b)关于原点成中心对称,则a+b的值为( )
A.-3 B.-1 C.1 D.3
3如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中 CD边上的高是____________.
第3题图 第4题图
4.如图,直线a,b垂直相交于点O,曲线C关于点O 成中心对称,点A 的对称点是点 A',AB⊥a于点B,A'D⊥b于点 D.若OB=4,OD=3,则阴影部分的面积之和为____________.
5.如图,△ABO与△CDO关于O 点中心对称,点E,F在线段 AC上,且AF=CE,求证:FD=BE.
知识点2 中心对称作图
6.如图,△ABC的顶点坐标分别为A(-3,3),B(0,1),C(-1,-1).
(1)请画出△ABC 关于点 B成中心对称的△A BC ,并写出点 A ,C 的坐标;
(2)四边形 AC A C的面积为____________.
知识点3 中心对称图形
7.北京冬奥会和冬残奥会组委会收到来自全球的会徽设计方案共 4 506件,其中很多设计方案体现了对称之美.以下4幅设计方案中,既是轴对称图形又是中心对称图形的是( )
8如图,图中阴影部分是由4个完全相同的正方形拼接而成的,若要在①②③④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在_________处(填写区域对应的序号).
刷提升
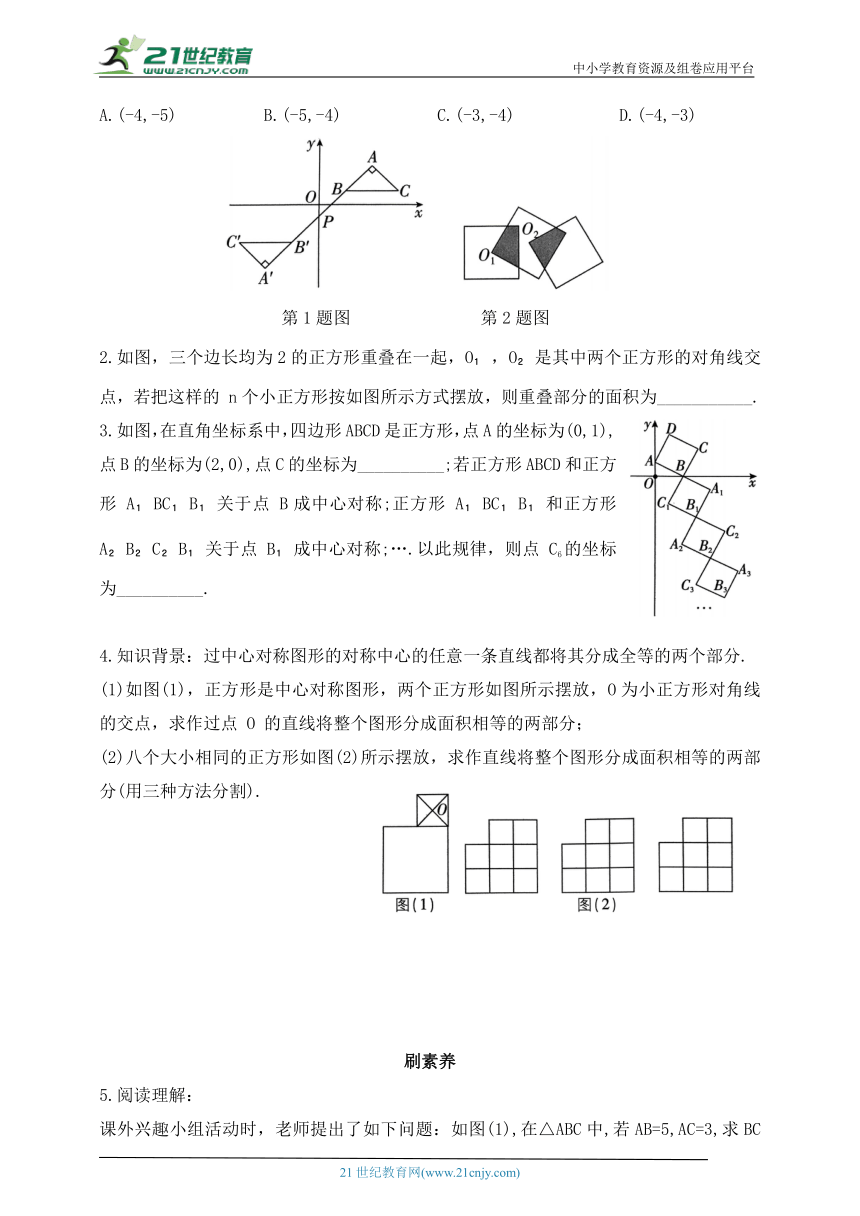
1.如图,在平面直角坐标系中,△ABC 的顶点 A 在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线 AB 交y轴于点 P,若△ABC与△A'B'C'关于点P成中心对称,则点 A'的坐标为( )
A.(-4,-5) B.(-5,-4) C.(-3,-4) D.(-4,-3)
第1题图 第2题图
2.如图,三个边长均为2的正方形重叠在一起,O ,O 是其中两个正方形的对角线交点,若把这样的 n个小正方形按如图所示方式摆放,则重叠部分的面积为___________.
3.如图,在直角坐标系中,四边形ABCD是正方形,点A的坐标为(0,1),点B的坐标为(2,0),点C的坐标为__________;若正方形ABCD和正方形 A BC B 关于点 B成中心对称;正方形 A BC B 和正方形 A B C B 关于点 B 成中心对称;….以此规律,则点 C6的坐标为__________.
4.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图(1),正方形是中心对称图形,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点 O 的直线将整个图形分成面积相等的两部分;
(2)八个大小相同的正方形如图(2)所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
刷素养
5.阅读理解:
课外兴趣小组活动时,老师提出了如下问题:如图(1),在△ABC中,若AB=5,AC=3,求BC边上的中线AD长的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:如图(1),延长AD到点 E,使得 DE=AD,再连接 BE(或将△ACD绕点 D旋转 180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系,可得2感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
解决问题:
受到以上启发,请你证明下列命题:如图(2),在△ABC中,D是 BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点 F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段 BE,CF,EF之间的等量关系,并加以证明.
参考答案
刷基础
1. C【解析】根据中心对称的概念,可得②③④中左边的图形与右边的图形成中心对称. 故选C.
2. C【解析】∵点A(a,1)与点 B(-2,b)关于原点成中心对称,∴a=2,b=-1,∴a+b=1,故选C.
3.4【解析】根据题意,得△DOC的面积等于△AOB的面积,均为6,CD=AB=3. 根据三角形的面积公式,可得CD边上的高是6×2÷3=4.故答案为 4.
4.12【解析】如图,过A作AE⊥b于E.∵直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点. 于点B, 于点D,OB=4,OD=3,∴AB=3,图形①与图形②面积相等,∴阴影部分的面积之和=长方形ABOE 的面积,即3×4=12.
故答案为12.
5.【证明】∵△ABO与△CDO 关于O 点中心对称,∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,∴FO=EO.
在△FOD和△EOB中 ∴△FOD≌△EOB(SAS),∴DF=BE.
6.【解】(1)如图,△A BC 即为所求.点A ,C 的坐标分别是A (3,-1),C (1,3).
(2)四边形 AC A C的面积为 4×4= 16.故答案为16.
7. C【解析】A 选项,既不是中心对称图形,也不是轴对称图形,故此选项不合题意;B选项,是中心对称图形,不是轴对称图形,故此选项不合题意;C选项,既是中心对称图形,也是轴对称图形,故此选项符合题意;D选项,既不是中心对称图形,也不是轴对称图形,故此选项不合题意.故选 C.
8.②【解析】把正方形添加在②处,则它与阴影部分组成的新图形是中心对称图形,故答案为②.
刷提升
1. A【解析】∵点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,∴△ABC是等腰直角三角形,∴易得A(4,3).设直线AB的表达式为 y=kx+b,则 解得
∴直线AB的表达式为y=x-1,令x=0,则y=-1,∴P(0,-1).又∵点A与点A'关于点P成中心对称,∴点P为AA'的中点. 设A'(m,n),则
故选A.
2. n-1【解析】连接O B,O C,如图.∵∠BO F+∠FO C = 90°,∠FO C +∠CO G= 90°,∴∠BO F=∠CO G.∵四边形ABCD是正方形,∴BO = CO ,∠O BF=∠O CG= 45°.在△O BF 和 △O CG 中, ∴△O BF≌△O CG(ASA),
∴四边形 GCFO 的面积是 同理另外两个正方形重叠部分的面积也是1,∴把这样的 n个小正方形按如图所示方式摆放,则重叠部分的面积为 n-1.故答案为 n-1.
3.(3,2)(9,-16)
【解析】如图所示,过点DC作DE⊥y轴,过点 C作CF⊥x轴,垂足分别为E,F.
∵四边形ABCD是正方形,点A 的坐标为(0,1),点B的坐标为(2,0),根据正方形的性质可知,△OAB≌△EDA≌△FBC,∴OF=3,CF=2,∴点C 的坐标为(3,2).
根据图象可得,C 与( 的横坐标相差4,纵坐标相差与C n的横坐标相差-2,纵坐标相差-4,∴C 的坐标为(1,-2),当n=1时,点C 的横坐标为1+4=5,纵坐标为-2-2=-4,故 C 的坐标为(5,-4).同理可得,点C 的坐标为(3,-8),点 C4的坐标为(7,-10),点C 的坐标为(5,-14),故点C 的坐标为(9,-16).故答案为(3,2),(9,-16).
4.【解】(1)如图(1)所示.
(2)如图(2)所示.
刷素养
5.(1)【证明】如图,延长 FD到 G,使得 DG=DF,连接 BG,EG(或把△CFD绕点 D 旋转 180°得到F△BGD). 易证 △CDF≌△BDG,∴CF=BG.∵ DE⊥DF,DF=DG,∴EF=EG.在△BEG中,BE+BG>EG,即GBE+CF>EF.
(2)【解】BE +CF =EF .证明如下:若∠A=90°,则∠EBC+∠FCB= 90°.
由①知∠FCD=∠DBG, EF= EG,∴ ∠EBC+∠DBG= 90°,即∠EBG=90°,
∴在 Rt△EBG中,BE +BG =EG ,∴BE +CF =EF .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 图形的平移与旋转
3 中心对称
刷基础
知识点1 中心对称的定义及性质
1.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2.在平面直角坐标系中,点A(a,1)与点 B(-2,b)关于原点成中心对称,则a+b的值为( )
A.-3 B.-1 C.1 D.3
3如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中 CD边上的高是____________.
第3题图 第4题图
4.如图,直线a,b垂直相交于点O,曲线C关于点O 成中心对称,点A 的对称点是点 A',AB⊥a于点B,A'D⊥b于点 D.若OB=4,OD=3,则阴影部分的面积之和为____________.
5.如图,△ABO与△CDO关于O 点中心对称,点E,F在线段 AC上,且AF=CE,求证:FD=BE.
知识点2 中心对称作图
6.如图,△ABC的顶点坐标分别为A(-3,3),B(0,1),C(-1,-1).
(1)请画出△ABC 关于点 B成中心对称的△A BC ,并写出点 A ,C 的坐标;
(2)四边形 AC A C的面积为____________.
知识点3 中心对称图形
7.北京冬奥会和冬残奥会组委会收到来自全球的会徽设计方案共 4 506件,其中很多设计方案体现了对称之美.以下4幅设计方案中,既是轴对称图形又是中心对称图形的是( )
8如图,图中阴影部分是由4个完全相同的正方形拼接而成的,若要在①②③④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在_________处(填写区域对应的序号).
刷提升
1.如图,在平面直角坐标系中,△ABC 的顶点 A 在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线 AB 交y轴于点 P,若△ABC与△A'B'C'关于点P成中心对称,则点 A'的坐标为( )
A.(-4,-5) B.(-5,-4) C.(-3,-4) D.(-4,-3)
第1题图 第2题图
2.如图,三个边长均为2的正方形重叠在一起,O ,O 是其中两个正方形的对角线交点,若把这样的 n个小正方形按如图所示方式摆放,则重叠部分的面积为___________.
3.如图,在直角坐标系中,四边形ABCD是正方形,点A的坐标为(0,1),点B的坐标为(2,0),点C的坐标为__________;若正方形ABCD和正方形 A BC B 关于点 B成中心对称;正方形 A BC B 和正方形 A B C B 关于点 B 成中心对称;….以此规律,则点 C6的坐标为__________.
4.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图(1),正方形是中心对称图形,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点 O 的直线将整个图形分成面积相等的两部分;
(2)八个大小相同的正方形如图(2)所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
刷素养
5.阅读理解:
课外兴趣小组活动时,老师提出了如下问题:如图(1),在△ABC中,若AB=5,AC=3,求BC边上的中线AD长的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:如图(1),延长AD到点 E,使得 DE=AD,再连接 BE(或将△ACD绕点 D旋转 180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系,可得2
解决问题:
受到以上启发,请你证明下列命题:如图(2),在△ABC中,D是 BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点 F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段 BE,CF,EF之间的等量关系,并加以证明.
参考答案
刷基础
1. C【解析】根据中心对称的概念,可得②③④中左边的图形与右边的图形成中心对称. 故选C.
2. C【解析】∵点A(a,1)与点 B(-2,b)关于原点成中心对称,∴a=2,b=-1,∴a+b=1,故选C.
3.4【解析】根据题意,得△DOC的面积等于△AOB的面积,均为6,CD=AB=3. 根据三角形的面积公式,可得CD边上的高是6×2÷3=4.故答案为 4.
4.12【解析】如图,过A作AE⊥b于E.∵直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点. 于点B, 于点D,OB=4,OD=3,∴AB=3,图形①与图形②面积相等,∴阴影部分的面积之和=长方形ABOE 的面积,即3×4=12.
故答案为12.
5.【证明】∵△ABO与△CDO 关于O 点中心对称,∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,∴FO=EO.
在△FOD和△EOB中 ∴△FOD≌△EOB(SAS),∴DF=BE.
6.【解】(1)如图,△A BC 即为所求.点A ,C 的坐标分别是A (3,-1),C (1,3).
(2)四边形 AC A C的面积为 4×4= 16.故答案为16.
7. C【解析】A 选项,既不是中心对称图形,也不是轴对称图形,故此选项不合题意;B选项,是中心对称图形,不是轴对称图形,故此选项不合题意;C选项,既是中心对称图形,也是轴对称图形,故此选项符合题意;D选项,既不是中心对称图形,也不是轴对称图形,故此选项不合题意.故选 C.
8.②【解析】把正方形添加在②处,则它与阴影部分组成的新图形是中心对称图形,故答案为②.
刷提升
1. A【解析】∵点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,∴△ABC是等腰直角三角形,∴易得A(4,3).设直线AB的表达式为 y=kx+b,则 解得
∴直线AB的表达式为y=x-1,令x=0,则y=-1,∴P(0,-1).又∵点A与点A'关于点P成中心对称,∴点P为AA'的中点. 设A'(m,n),则
故选A.
2. n-1【解析】连接O B,O C,如图.∵∠BO F+∠FO C = 90°,∠FO C +∠CO G= 90°,∴∠BO F=∠CO G.∵四边形ABCD是正方形,∴BO = CO ,∠O BF=∠O CG= 45°.在△O BF 和 △O CG 中, ∴△O BF≌△O CG(ASA),
∴四边形 GCFO 的面积是 同理另外两个正方形重叠部分的面积也是1,∴把这样的 n个小正方形按如图所示方式摆放,则重叠部分的面积为 n-1.故答案为 n-1.
3.(3,2)(9,-16)
【解析】如图所示,过点DC作DE⊥y轴,过点 C作CF⊥x轴,垂足分别为E,F.
∵四边形ABCD是正方形,点A 的坐标为(0,1),点B的坐标为(2,0),根据正方形的性质可知,△OAB≌△EDA≌△FBC,∴OF=3,CF=2,∴点C 的坐标为(3,2).
根据图象可得,C 与( 的横坐标相差4,纵坐标相差与C n的横坐标相差-2,纵坐标相差-4,∴C 的坐标为(1,-2),当n=1时,点C 的横坐标为1+4=5,纵坐标为-2-2=-4,故 C 的坐标为(5,-4).同理可得,点C 的坐标为(3,-8),点 C4的坐标为(7,-10),点C 的坐标为(5,-14),故点C 的坐标为(9,-16).故答案为(3,2),(9,-16).
4.【解】(1)如图(1)所示.
(2)如图(2)所示.
刷素养
5.(1)【证明】如图,延长 FD到 G,使得 DG=DF,连接 BG,EG(或把△CFD绕点 D 旋转 180°得到F△BGD). 易证 △CDF≌△BDG,∴CF=BG.∵ DE⊥DF,DF=DG,∴EF=EG.在△BEG中,BE+BG>EG,即GBE+CF>EF.
(2)【解】BE +CF =EF .证明如下:若∠A=90°,则∠EBC+∠FCB= 90°.
由①知∠FCD=∠DBG, EF= EG,∴ ∠EBC+∠DBG= 90°,即∠EBG=90°,
∴在 Rt△EBG中,BE +BG =EG ,∴BE +CF =EF .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
