11.1 柱体(第1课时) 课件(共38张PPT)
文档属性
| 名称 | 11.1 柱体(第1课时) 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 00:00:00 | ||
图片预览








文档简介
(共38张PPT)
11.1柱体(第1课时)
11.1.1棱柱与圆柱-11.1.2空间图形的平面直观图画法
第11章 简单几何体
沪教版(2020) 必修第三册
棱柱及其结构
空间图形的平面直观图画法
圆柱及其结构
01
03
02
CONTANTS
目 录
棱柱及其结构
01
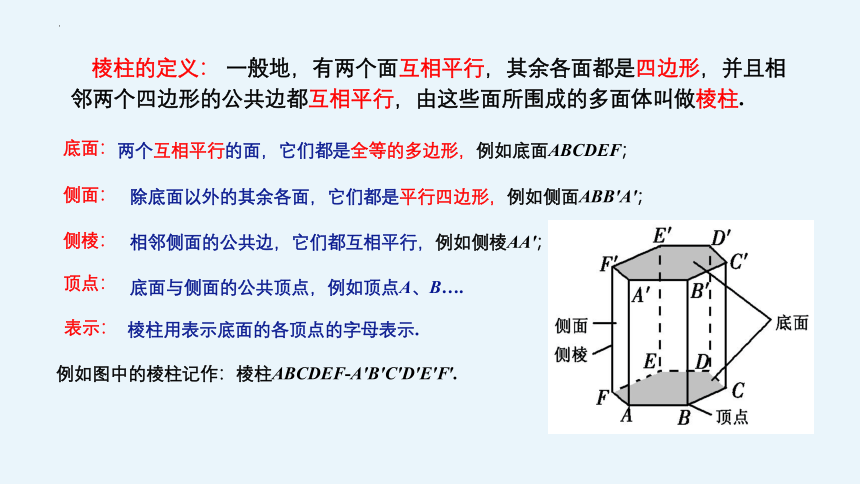
棱柱的定义: 一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.
两个互相平行的面,它们都是全等的多边形,例如底面ABCDEF;
底面:
侧面:
侧棱:
顶点:
底面与侧面的公共顶点,例如顶点A、B….
除底面以外的其余各面,它们都是平行四边形,例如侧面ABB′A′;
相邻侧面的公共边,它们都互相平行,例如侧棱AA′;
表示:
棱柱用表示底面的各顶点的字母表示.
例如图中的棱柱记作:棱柱ABCDEF-A′B′C′D′E′F′.
满足“ 有两个面相互平行,其余各面都是平行四边形的几何体 ”这样说法的还有右图的情况,如图所示,所以定义中不能简单描述成“其余各面都是平行四边形 。.
为什么定义中要说‘‘其余各面都是四边形,并且相邻两个四边形的公共边都相互平行'',而不简单的只说 “ 其余各面是平行四边形呢 ” ?
棱柱的结构特征
两底面互相平行且全等
各侧面都是平行四边形
各侧棱互相平行且相等
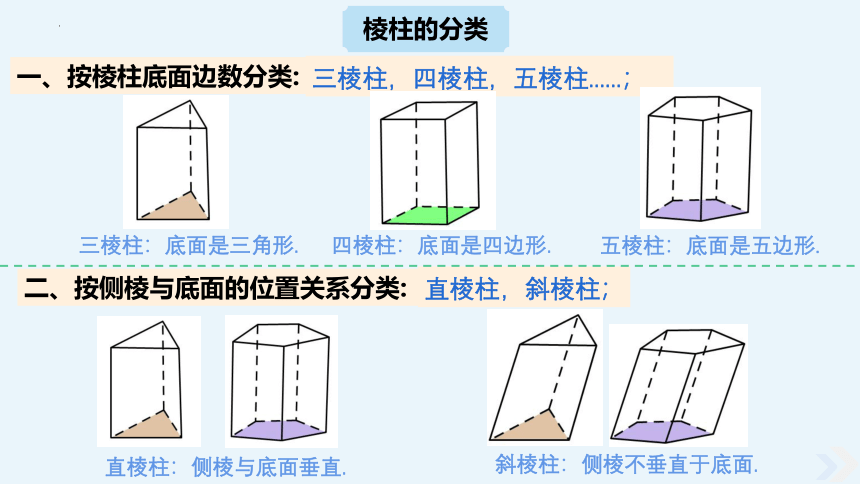
棱柱的分类
一、按棱柱底面边数分类:
三棱柱,四棱柱,五棱柱......;
五棱柱:底面是五边形.
四棱柱:底面是四边形.
三棱柱:底面是三角形.
直棱柱,斜棱柱;
二、按侧棱与底面的位置关系分类:
斜棱柱:侧棱不垂直于底面.
直棱柱:侧棱与底面垂直.
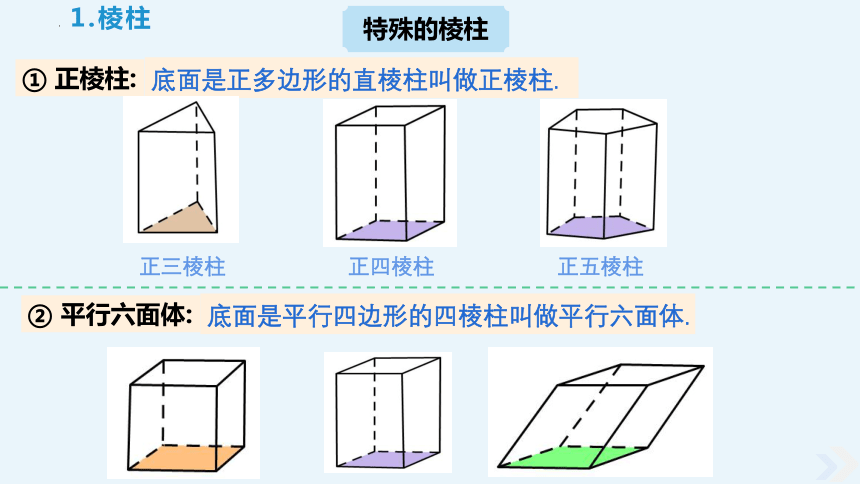
1.棱柱
特殊的棱柱
① 正棱柱:
底面是正多边形的直棱柱叫做正棱柱.
正五棱柱
正四棱柱
正三棱柱
② 平行六面体:
底面是平行四边形的四棱柱叫做平行六面体.
平行六面体
斜棱柱
棱柱
直棱柱
侧棱垂直底面
侧棱不垂直底面
底面是平行四边形
底面是正边形
正棱柱
底面是矩形
长方体
正方体
各棱长都相等
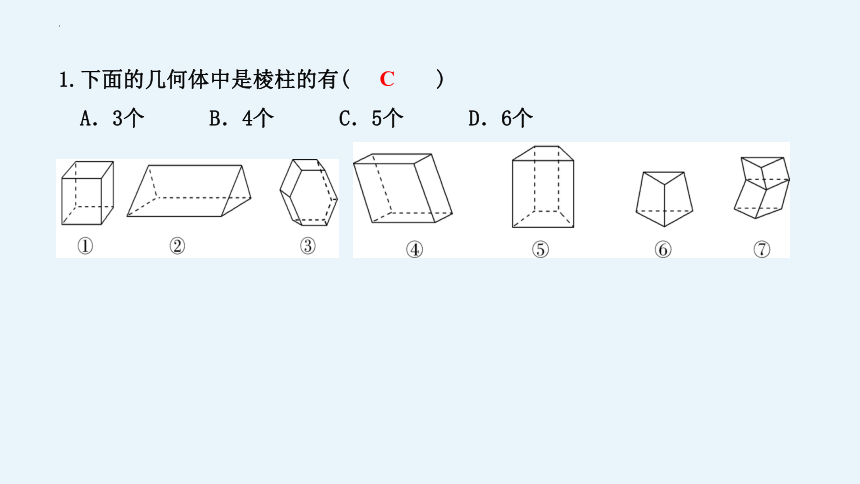
1.下面的几何体中是棱柱的有( )
A.3个 B.4个 C.5个 D.6个
C
例1.下列说法正确的是( ).
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
D
例2.下列命题中,正确的是( ).
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
D
(1)看“面”:
观察这个多面体是否有两个互相平行的面,其余各面都是四边形
(2)看“线” :
在察每相邻两个四边形的公共边是否平行
(3) 举反例 :
通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除
思维升华:准确认识棱柱的结构特征
圆柱及其结构
02
1.圆柱的定义:以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱。
(1)旋转轴叫做圆柱的轴。
(2) 垂直于轴的边旋转而成的圆面叫做圆柱的底面。
(3)平行于轴的边旋转而成的曲面叫做圆柱的侧面。
(4)无论旋转到什么位置,平行于轴的边都叫做圆柱侧面的母线。
侧面
轴
母线
底面
母线
圆柱的表示:
用表示它的轴
的字母表示。
圆柱的结构特征
(1)底面是平行且半径相等的圆面.
(2)侧面展开图是矩形面.
(3)母线平行且相等.
(4)平行于底面的截面是与底面平行且半径相等的圆面.
(5)轴截面是矩形面.
圆柱常见截面图
横截面
轴截面
斜截面
B
空间图形的平面直观图画法
03
直观图:表示空间几何图形的平面图形,叫做空间图形的直观图
直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到
的平面图形
直观图的画法
斜二侧画法
观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?
平行四边形
探究1:水平放置的平面图形的直观图斜二测画法
(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。
(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。
(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。
对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,
这与我们的直观观察是一致的。
A
D'
C'
D
B'
A’
C
B
例一:用斜二测画法画水平放置的六边形的直观图
(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°
(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'= MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。
(3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F'
平面图形的斜二测画法
(1)建两个坐标系,注意斜坐标系夹角为450或1350;
(3)水平线段等长,竖直线段减半;
(2)与坐标轴平行或重合的线段保持平行或重合;
简言之:“横不变,竖减半,平行、重合不改变。”
(4)整理.
步骤:
关于水平放置的圆的直观图的画法,常用正等测画法.在实际画水平放置的圆的直观图时,通常使用椭圆模版.
说明:
用斜二测画法画边长为2cm的正三角形的直观图
练习一
A'
B'
C'
解:
例二:如何画出长,宽,高分别是3cm,2cm,1.5cm的长方体的直观图?
探究2:空间几何体的直观图画法
(1)画轴:画x轴、y轴、z轴,三轴交于一点O, 使 , 。
x
z
y
O
(2)画底面:以O为中心,在x轴上取线段MN,使MN=3cm;在y轴上取线段PQ,使PQ=1cm。分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A,B,C,D,四边形ABCD就是长方体的底面。
O
M
N
x
y
z
P
Q
A
B
C
D
(3)画侧棱:过A,B,C,D各点分别作z轴的平行线,并在这些平行线上分别截取1.5cm长的线段AA',BB',CC',DD'。
O
M
N
x
y
z
P
Q
A
B
C
D
A’
B’
C’
D’
(4)成图:顺次连接A',B',C',D',并去掉辅助线和坐标系,将被遮挡的部分改为虚线,即得到长方体的直观图。
O
M
N
x
y
z
P
Q
A
B
C
D
A’
B’
C’
D’
A
B
C
D
A’
C’
D’
(4)成图:顺次连接A',B',C',D',并去掉辅助线和坐标系,将被遮挡的部分改为虚线,即得到长方体的直观图。
画空间几何体直观图的步骤:
(1)画轴:画x轴、y轴、z轴,使∠xoy=450,∠xoz=900,把xoy所在平面视为水平面,xoz平面和yoz平面都是竖直面;
(3)画侧棱:过下底面多变的顶点分别作z轴的平行线段,长度与几何体中的相应线段长度一样;
(2)画底面:在xoy平面上用斜二测画法作出几何体的下底面;
(4)成图:连接侧棱的上端点,去掉辅助线和坐标系,并把遮挡的部分改为虚线。
简言之:先轴,后底,再侧棱,横纵不变,竖折半,平行、重合不改变。
1.画出下列图形的直观图:(1)棱长为4cm的正方体;(2)底面半径为2cm,高为4cm的圆锥.
【答案】(1)画法见解析,
3.边长为2的正三角形,其水平放置的直观图的面积为( )
D
D
B
B
C
11.1柱体(第1课时)
11.1.1棱柱与圆柱-11.1.2空间图形的平面直观图画法
第11章 简单几何体
沪教版(2020) 必修第三册
棱柱及其结构
空间图形的平面直观图画法
圆柱及其结构
01
03
02
CONTANTS
目 录
棱柱及其结构
01
棱柱的定义: 一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.
两个互相平行的面,它们都是全等的多边形,例如底面ABCDEF;
底面:
侧面:
侧棱:
顶点:
底面与侧面的公共顶点,例如顶点A、B….
除底面以外的其余各面,它们都是平行四边形,例如侧面ABB′A′;
相邻侧面的公共边,它们都互相平行,例如侧棱AA′;
表示:
棱柱用表示底面的各顶点的字母表示.
例如图中的棱柱记作:棱柱ABCDEF-A′B′C′D′E′F′.
满足“ 有两个面相互平行,其余各面都是平行四边形的几何体 ”这样说法的还有右图的情况,如图所示,所以定义中不能简单描述成“其余各面都是平行四边形 。.
为什么定义中要说‘‘其余各面都是四边形,并且相邻两个四边形的公共边都相互平行'',而不简单的只说 “ 其余各面是平行四边形呢 ” ?
棱柱的结构特征
两底面互相平行且全等
各侧面都是平行四边形
各侧棱互相平行且相等
棱柱的分类
一、按棱柱底面边数分类:
三棱柱,四棱柱,五棱柱......;
五棱柱:底面是五边形.
四棱柱:底面是四边形.
三棱柱:底面是三角形.
直棱柱,斜棱柱;
二、按侧棱与底面的位置关系分类:
斜棱柱:侧棱不垂直于底面.
直棱柱:侧棱与底面垂直.
1.棱柱
特殊的棱柱
① 正棱柱:
底面是正多边形的直棱柱叫做正棱柱.
正五棱柱
正四棱柱
正三棱柱
② 平行六面体:
底面是平行四边形的四棱柱叫做平行六面体.
平行六面体
斜棱柱
棱柱
直棱柱
侧棱垂直底面
侧棱不垂直底面
底面是平行四边形
底面是正边形
正棱柱
底面是矩形
长方体
正方体
各棱长都相等
1.下面的几何体中是棱柱的有( )
A.3个 B.4个 C.5个 D.6个
C
例1.下列说法正确的是( ).
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
D
例2.下列命题中,正确的是( ).
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
D
(1)看“面”:
观察这个多面体是否有两个互相平行的面,其余各面都是四边形
(2)看“线” :
在察每相邻两个四边形的公共边是否平行
(3) 举反例 :
通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除
思维升华:准确认识棱柱的结构特征
圆柱及其结构
02
1.圆柱的定义:以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱。
(1)旋转轴叫做圆柱的轴。
(2) 垂直于轴的边旋转而成的圆面叫做圆柱的底面。
(3)平行于轴的边旋转而成的曲面叫做圆柱的侧面。
(4)无论旋转到什么位置,平行于轴的边都叫做圆柱侧面的母线。
侧面
轴
母线
底面
母线
圆柱的表示:
用表示它的轴
的字母表示。
圆柱的结构特征
(1)底面是平行且半径相等的圆面.
(2)侧面展开图是矩形面.
(3)母线平行且相等.
(4)平行于底面的截面是与底面平行且半径相等的圆面.
(5)轴截面是矩形面.
圆柱常见截面图
横截面
轴截面
斜截面
B
空间图形的平面直观图画法
03
直观图:表示空间几何图形的平面图形,叫做空间图形的直观图
直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到
的平面图形
直观图的画法
斜二侧画法
观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?
平行四边形
探究1:水平放置的平面图形的直观图斜二测画法
(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。
(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。
(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。
对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,
这与我们的直观观察是一致的。
A
D'
C'
D
B'
A’
C
B
例一:用斜二测画法画水平放置的六边形的直观图
(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°
(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'= MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。
(3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F'
平面图形的斜二测画法
(1)建两个坐标系,注意斜坐标系夹角为450或1350;
(3)水平线段等长,竖直线段减半;
(2)与坐标轴平行或重合的线段保持平行或重合;
简言之:“横不变,竖减半,平行、重合不改变。”
(4)整理.
步骤:
关于水平放置的圆的直观图的画法,常用正等测画法.在实际画水平放置的圆的直观图时,通常使用椭圆模版.
说明:
用斜二测画法画边长为2cm的正三角形的直观图
练习一
A'
B'
C'
解:
例二:如何画出长,宽,高分别是3cm,2cm,1.5cm的长方体的直观图?
探究2:空间几何体的直观图画法
(1)画轴:画x轴、y轴、z轴,三轴交于一点O, 使 , 。
x
z
y
O
(2)画底面:以O为中心,在x轴上取线段MN,使MN=3cm;在y轴上取线段PQ,使PQ=1cm。分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A,B,C,D,四边形ABCD就是长方体的底面。
O
M
N
x
y
z
P
Q
A
B
C
D
(3)画侧棱:过A,B,C,D各点分别作z轴的平行线,并在这些平行线上分别截取1.5cm长的线段AA',BB',CC',DD'。
O
M
N
x
y
z
P
Q
A
B
C
D
A’
B’
C’
D’
(4)成图:顺次连接A',B',C',D',并去掉辅助线和坐标系,将被遮挡的部分改为虚线,即得到长方体的直观图。
O
M
N
x
y
z
P
Q
A
B
C
D
A’
B’
C’
D’
A
B
C
D
A’
C’
D’
(4)成图:顺次连接A',B',C',D',并去掉辅助线和坐标系,将被遮挡的部分改为虚线,即得到长方体的直观图。
画空间几何体直观图的步骤:
(1)画轴:画x轴、y轴、z轴,使∠xoy=450,∠xoz=900,把xoy所在平面视为水平面,xoz平面和yoz平面都是竖直面;
(3)画侧棱:过下底面多变的顶点分别作z轴的平行线段,长度与几何体中的相应线段长度一样;
(2)画底面:在xoy平面上用斜二测画法作出几何体的下底面;
(4)成图:连接侧棱的上端点,去掉辅助线和坐标系,并把遮挡的部分改为虚线。
简言之:先轴,后底,再侧棱,横纵不变,竖折半,平行、重合不改变。
1.画出下列图形的直观图:(1)棱长为4cm的正方体;(2)底面半径为2cm,高为4cm的圆锥.
【答案】(1)画法见解析,
3.边长为2的正三角形,其水平放置的直观图的面积为( )
D
D
B
B
C
同课章节目录
