24.2.2直线和圆的位置关系(海南省琼海市)
文档属性
| 名称 | 24.2.2直线和圆的位置关系(海南省琼海市) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-23 00:00:00 | ||
图片预览




文档简介
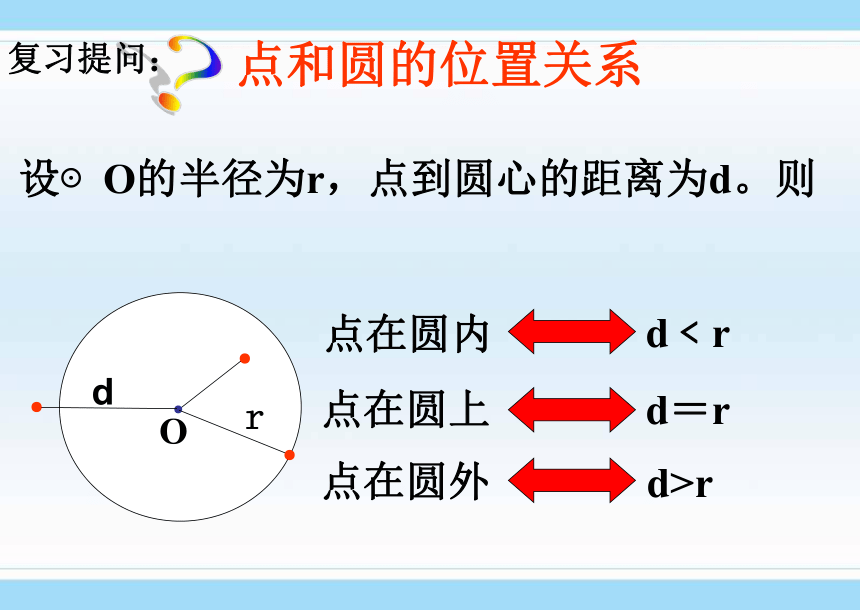
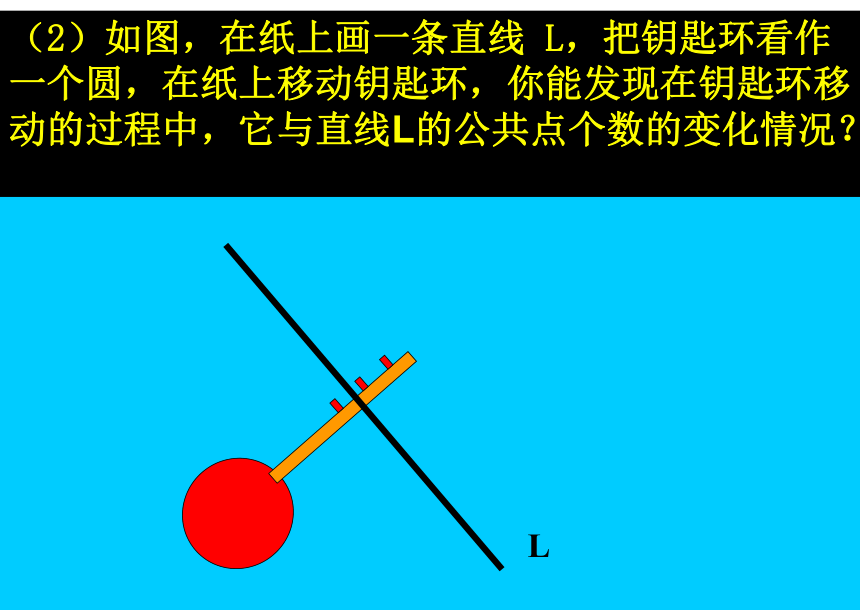
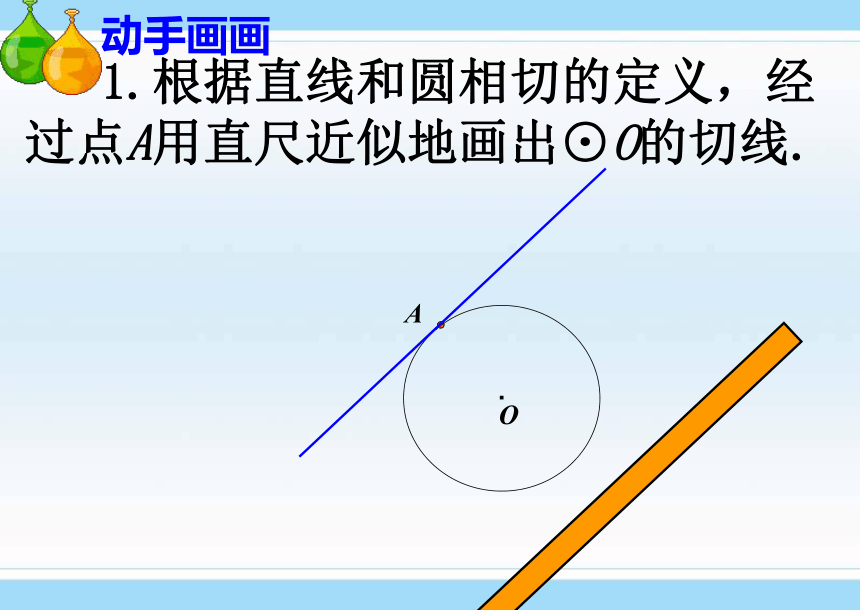
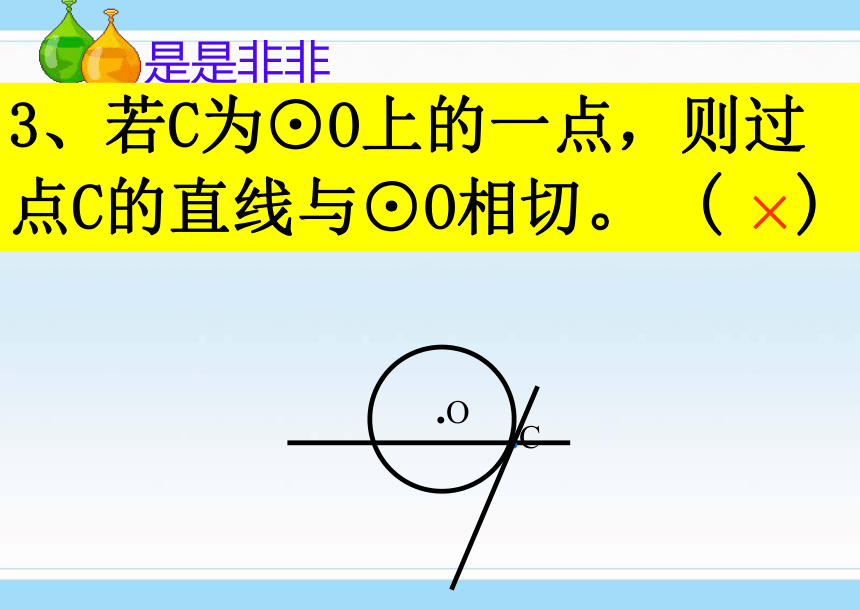
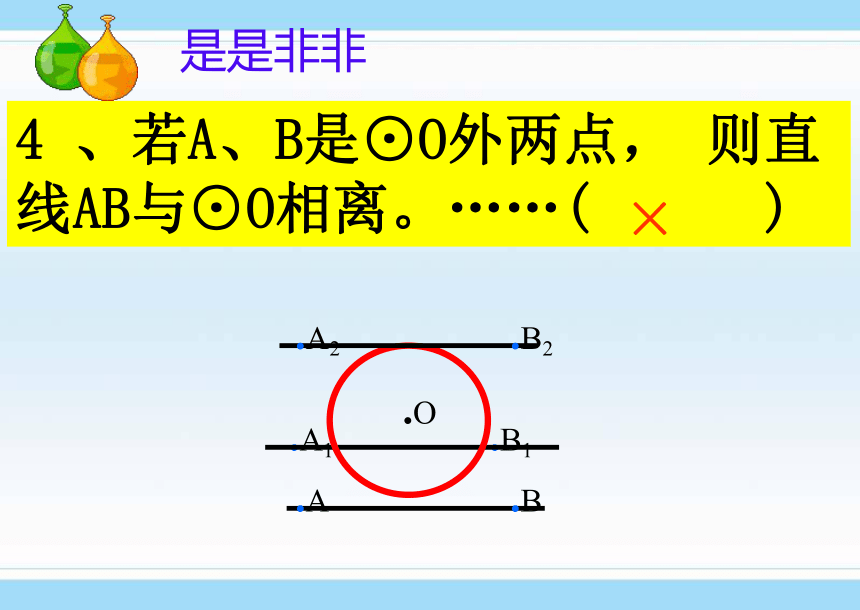
课件22张PPT。24.2.1直线和圆的位置关系24.2.1直线和圆的位置关系授课教师 刘红军设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r●●●●Od?复习提问:r(1)如图,我们把太阳看作一个圆,地平线看作一条直线,在太阳升起的过程中,太阳和地平线的公共点个数有几种情况?(2)如图,在纸上画一条直线 L,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线L的公共点个数的变化情况?L直线和圆有两个公共点,这时我们说直线和圆相交,这条直线叫做圆的割线.(如图3)直线和圆只有一个公共点,这时我们说直线和圆相切,这条直线叫做圆的切线,这个点叫做切点. (如图2)直线和圆没有公共点,这时我们说直线和圆相离.如图1图1图2图3●Alll●A●B 1.根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.O动手画画.O是是非非 2、直线与圆最多有两个公共点 。( ) √.O是是非非.C3、若C为⊙O上的一点,则过点C的直线与⊙O相切。 ( )×是是非非4 、若A、B是⊙O外两点, 则直线AB与⊙O相离。……( )×.O是是非非5、若C为⊙O内一点,则过点C的直线与⊙O相交。( ).O√ 知识总结:根据定义:我们可以根据直线与圆的公共点的个数来判断直线与圆的位置关系.新的问题:在直线与圆的不同位置关系时,直线到圆心的距离与半径之间是不是也具有一定的大小关系呢?dr相离d相切LL直线与圆的位置关系 (数量特征).Od相交.OOLrr如图:d表示圆心O到直线L的距离,r表示⊙O的半径1.圆的半径是6.5cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系?有几个公共点?有两个公共点;有一个公共点;没有公共点.解:∴直线与圆相交∴直线与圆相切∴直线与圆相离填空:1、已知⊙O的半径为5cm,O到直线L的距离为3cm,则⊙O与直线L的位置关系是_____。直线L与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线L的距离是4cm,则⊙O与直线L的位置关系是 ___ 。动动脑筋相交 相切两个3、已知⊙O的直径为10cm,点O到直线L的距离为7cm,则⊙O与直线L的位置关系是 ;直线L与⊙O的公共点个数是____。零相离4、直线m上一点A到圆心O的距离等于⊙O的半径,则直线m与⊙O的位置关系是 。相切 或相交填空:动动脑筋归纳与小结相交相切相离2个交点d < r割线1个切点d = r切线0个d > r1.直线与圆的位置关系表:2、判定直线 与圆的位置关系的方法有____种:(1)根据定义,由__________________的个数来判断;(2)根据性质,由_____________________ ______________的大小关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r② 、已知圆的半径 r为6cm,设直线和圆心的距离为d :3)若d=8cm , 则直线与圆______, 直线与圆有___个公共点. 2)若d=6cm , 则直线与圆______, 直线与圆有____个公共点. 1)若d=4cm , 则直线与圆 , 直线与圆有____个公共点. 相交相切相离3、巩固练习210①.直线和圆有2个公共点,则直线和圆_________;
直线和圆只有1个公共点,则直线和圆_______;
直线和圆没有公共点,则直线和圆_________相交相切相离2)若AB和⊙O相切, 则 ;3)若AB和⊙O相交,则 .③、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ; d > 5cmd = 5cmd < 5cm0cm≤(1)、设⊙O的半径为r,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d与r
的关系是……………………( )
A、d≤r B、d<r C、d≥r D、d=r(2)、设⊙O的半径为r,直线a上一点到圆心
的距离为d,若d=r,则直线a与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交CD4、拓展练习(3).已知∠OAB = 30°,OA = 10,则以O为圆心,6为半径的圆与射线AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
(4).设圆的直径长为a,一条直线和圆有公共点,直线和圆心的距离为d,则( )
d< B d ≤ C. d = D.d >
(5).以P(3,4)为圆心的圆与x轴相切,则这个圆与y轴的关系是( )
A.相离 B.相切 C.相交 D.无法确定ABA 希望大家如这朝阳,
越升越高!越开越艳!
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系?有几个公共点?有两个公共点;有一个公共点;没有公共点.解:∴直线与圆相交∴直线与圆相切∴直线与圆相离填空:1、已知⊙O的半径为5cm,O到直线L的距离为3cm,则⊙O与直线L的位置关系是_____。直线L与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线L的距离是4cm,则⊙O与直线L的位置关系是 ___ 。动动脑筋相交 相切两个3、已知⊙O的直径为10cm,点O到直线L的距离为7cm,则⊙O与直线L的位置关系是 ;直线L与⊙O的公共点个数是____。零相离4、直线m上一点A到圆心O的距离等于⊙O的半径,则直线m与⊙O的位置关系是 。相切 或相交填空:动动脑筋归纳与小结相交相切相离2个交点d < r割线1个切点d = r切线0个d > r1.直线与圆的位置关系表:2、判定直线 与圆的位置关系的方法有____种:(1)根据定义,由__________________的个数来判断;(2)根据性质,由_____________________ ______________的大小关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r② 、已知圆的半径 r为6cm,设直线和圆心的距离为d :3)若d=8cm , 则直线与圆______, 直线与圆有___个公共点. 2)若d=6cm , 则直线与圆______, 直线与圆有____个公共点. 1)若d=4cm , 则直线与圆 , 直线与圆有____个公共点. 相交相切相离3、巩固练习210①.直线和圆有2个公共点,则直线和圆_________;
直线和圆只有1个公共点,则直线和圆_______;
直线和圆没有公共点,则直线和圆_________相交相切相离2)若AB和⊙O相切, 则 ;3)若AB和⊙O相交,则 .③、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ; d > 5cmd = 5cmd < 5cm0cm≤(1)、设⊙O的半径为r,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d与r
的关系是……………………( )
A、d≤r B、d<r C、d≥r D、d=r(2)、设⊙O的半径为r,直线a上一点到圆心
的距离为d,若d=r,则直线a与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交CD4、拓展练习(3).已知∠OAB = 30°,OA = 10,则以O为圆心,6为半径的圆与射线AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
(4).设圆的直径长为a,一条直线和圆有公共点,直线和圆心的距离为d,则( )
d< B d ≤ C. d = D.d >
(5).以P(3,4)为圆心的圆与x轴相切,则这个圆与y轴的关系是( )
A.相离 B.相切 C.相交 D.无法确定ABA 希望大家如这朝阳,
越升越高!越开越艳!
同课章节目录
