2023-2024学年人教版九年级数学上册 第二十二章 二次函数单元复习(无答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册 第二十二章 二次函数单元复习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 266.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 09:01:18 | ||
图片预览

文档简介
九年级上册 《二十二章 二次函数》单元复习
一、选择题
1. 下列函数中,是二次函数的是( )
A. B. C. D.
2. 把抛物线向右平移个单位,再向下平移个单位,得到抛物线( )
A. B.
C. D.
3.下列二次函数中,其图象的对称轴为x=﹣2的是( )
A.y=2x2﹣2 B.y=﹣2x2﹣2 C.y=2 (x﹣2)2 D.y=(x+2)2
4.抛物线y=x2﹣2x+1与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
5.对于抛物线,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>-1时,y随x的增大而减小,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
6.已知二次函数的图象经过原点,则的值为( )
A.0或2 B.0 C.2 D.无法确定
已知抛物线,若点与点Q关于该抛物线的对称轴对称,则点Q的坐标是( ).
A. B. C. D.
8.抛物线与x轴有两个交点,则a的取值范围是( ).
A. B. C. D.且
9.二次函数的图象如图所示,则下列结论中不正确的是( )
A. B.函数的最大值为
C.当x>3时,y<0 D.
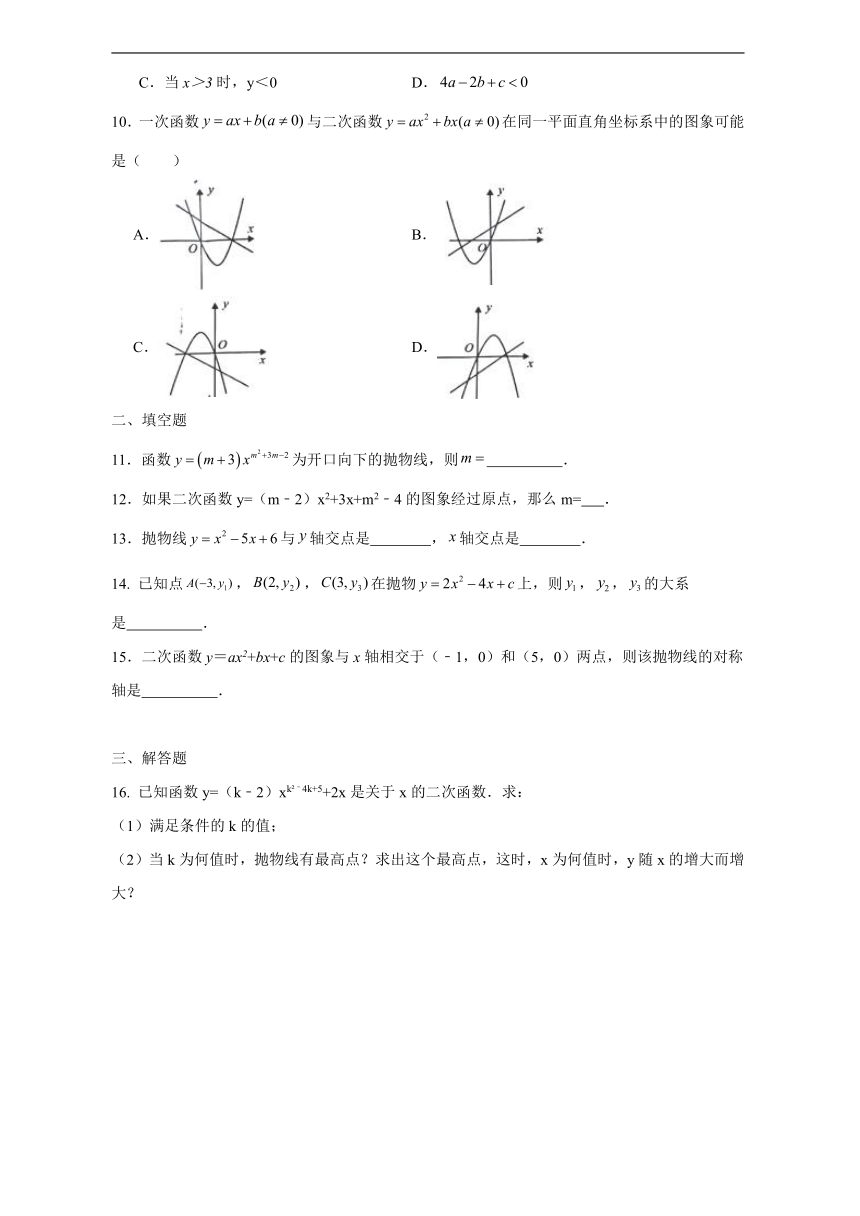
10.一次函数与二次函数在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
二、填空题
11.函数为开口向下的抛物线,则 .
12.如果二次函数y=(m﹣2)x2+3x+m2﹣4的图象经过原点,那么m= .
13.抛物线与轴交点是 ,轴交点是 .
14. 已知点,,在抛物上,则,,的大系是 .
15.二次函数y=ax2+bx+c的图象与x轴相交于(﹣1,0)和(5,0)两点,则该抛物线的对称轴是 .
三、解答题
16. 已知函数y=(k﹣2)xk ﹣4k+5+2x是关于x的二次函数.求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点,这时,x为何值时,y随x的增大而增大?
试卷第1页,共3页
如图,抛物线y=x2+x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)求点A,点B和点C的坐标;
(2)抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标.
体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处点距离地面的高度为,当球运行的水平距离为时,达到最大高度的处(如图),问该学生把实心球扔出多远?(结果保留根号)
如图,抛物线经过点,与轴交于点
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
过点且平行于轴的直线交抛物线于点.
(1)求抛物线的解析式;
(2)求的面积;
(3)在该抛物线的对称轴上是否存在点,使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.
某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)商场如何设计方案才能获得最大利润,最大利润是多少?
23.某电商销售某种商品一段时间后,发现该商品每天的销售量y(单位:千克)和每千克的售价x(单位:元)满足一次函数关系(如图所示),其中,
(1)求y关于x的函数解析式;
(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大?最大利润是多少?
24.如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
.
一、选择题
1. 下列函数中,是二次函数的是( )
A. B. C. D.
2. 把抛物线向右平移个单位,再向下平移个单位,得到抛物线( )
A. B.
C. D.
3.下列二次函数中,其图象的对称轴为x=﹣2的是( )
A.y=2x2﹣2 B.y=﹣2x2﹣2 C.y=2 (x﹣2)2 D.y=(x+2)2
4.抛物线y=x2﹣2x+1与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
5.对于抛物线,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>-1时,y随x的增大而减小,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
6.已知二次函数的图象经过原点,则的值为( )
A.0或2 B.0 C.2 D.无法确定
已知抛物线,若点与点Q关于该抛物线的对称轴对称,则点Q的坐标是( ).
A. B. C. D.
8.抛物线与x轴有两个交点,则a的取值范围是( ).
A. B. C. D.且
9.二次函数的图象如图所示,则下列结论中不正确的是( )
A. B.函数的最大值为
C.当x>3时,y<0 D.
10.一次函数与二次函数在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
二、填空题
11.函数为开口向下的抛物线,则 .
12.如果二次函数y=(m﹣2)x2+3x+m2﹣4的图象经过原点,那么m= .
13.抛物线与轴交点是 ,轴交点是 .
14. 已知点,,在抛物上,则,,的大系是 .
15.二次函数y=ax2+bx+c的图象与x轴相交于(﹣1,0)和(5,0)两点,则该抛物线的对称轴是 .
三、解答题
16. 已知函数y=(k﹣2)xk ﹣4k+5+2x是关于x的二次函数.求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点,这时,x为何值时,y随x的增大而增大?
试卷第1页,共3页
如图,抛物线y=x2+x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)求点A,点B和点C的坐标;
(2)抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标.
体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处点距离地面的高度为,当球运行的水平距离为时,达到最大高度的处(如图),问该学生把实心球扔出多远?(结果保留根号)
如图,抛物线经过点,与轴交于点
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
过点且平行于轴的直线交抛物线于点.
(1)求抛物线的解析式;
(2)求的面积;
(3)在该抛物线的对称轴上是否存在点,使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.
某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)商场如何设计方案才能获得最大利润,最大利润是多少?
23.某电商销售某种商品一段时间后,发现该商品每天的销售量y(单位:千克)和每千克的售价x(单位:元)满足一次函数关系(如图所示),其中,
(1)求y关于x的函数解析式;
(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大?最大利润是多少?
24.如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
.
同课章节目录
