2.5.2圆与圆的位置关系 课件(共17张PPT)
文档属性
| 名称 | 2.5.2圆与圆的位置关系 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 684.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 14:00:09 | ||
图片预览




文档简介
(共17张PPT)
2.5.2
圆与圆的位置关系
人教A版(2019)选择性必修第一册
学习目标
1.能根据给定圆的方程,判断圆与圆的位置关系。
2.圆与圆位置关系的其判定方法。
3.用坐标法探求圆与圆位置关系的过程。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
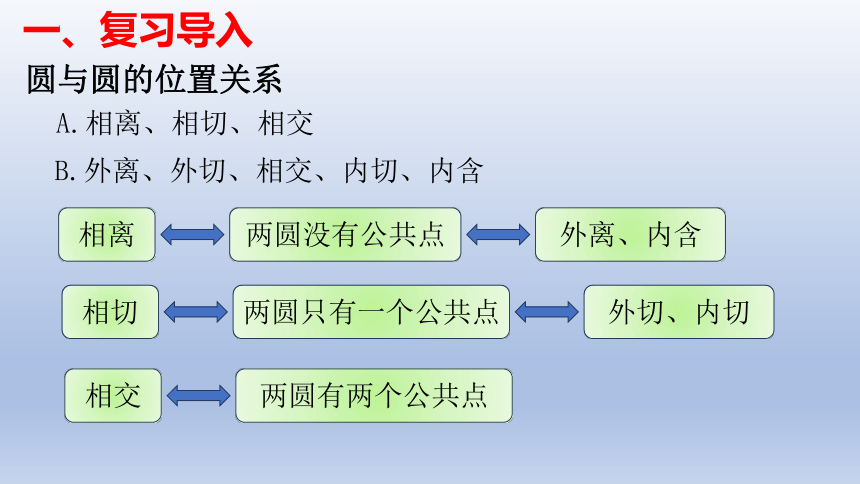
圆与圆的位置关系
A.相离、相切、相交
B.外离、外切、相交、内切、内含
相离
两圆没有公共点
外离、内含
相切
两圆只有一个公共点
外切、内切
相交
两圆有两个公共点
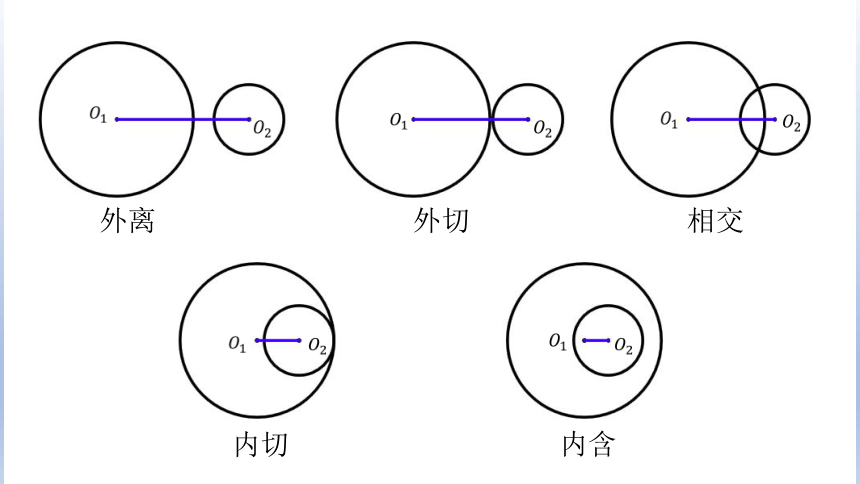
相交
外离
外切
内切
内含
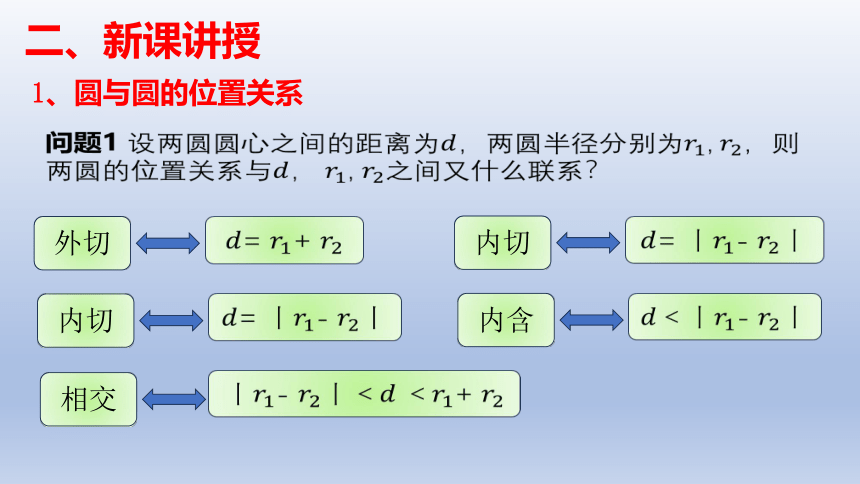
问题1 设两圆圆心之间的距离为,两圆半径分别为, ,则两圆的位置关系与, , 之间又什么联系?
二、新课讲授
1、圆与圆的位置关系
外切
= +
内切
= - 丨
相交
- 丨+
内切
= - 丨
内含
<- 丨
例1:已知圆,圆,试判断圆与圆的位置关系.
分析:
法1:可通过两圆心之间的距离与两半径之和或之差进行比较,得到两圆位置关系.
①需求出两圆心的坐标即两圆的半径;
②可将圆的方程化为标准方程.
法2:可通过两圆公共点的个数来判断两圆位置关系.
①联立两圆方程,解方程组;
②由方程组解的情况来判断位置关系.
解法一:圆的方程可化为: 的圆心为(-1,-4),半径5.
圆的方程可化为: 的圆心为(2,2),半径.
则= .
与圆的两半径之和为: + =5+
与圆的两半径之差为: - =5-
5- < < 5+ ,即- < < + ,
所以与圆有两个公共点,两圆相交.
解法二:将两圆方程联立,得
①-②,得
由=.代入①,并整理得:
因为方程的>0,所以方程有两个不相等的实数根, .
解得3, -1,分别代入方程③,解得-1, 1.
所以与圆有两个公共点,分别为(-1,1),(3,-1),两圆相交.
追问1:你能求出公共弦所在直线方程吗?
解:因为两圆的两个交点(-1,1),(3,-1)在公共弦上,
所以根据两点式可得公共弦所在直线的方程为:
追问2:方程与①-②得到方程一致,是巧合吗?
两圆相交时,公共弦所在直线方程就是两圆方程之差所得到的方程.
追问3:如果所求=0或<0,说明什么?
当=0时,方程只有一个实数解,即两圆只有一个公共点,故两圆内切或外切.
当<0时,方程没有实数解,即两圆没有公共点,故两圆内含或外离.
要想得到更确切的位置,还需要通过圆心距与两半径之和或之差进行比较来判断.
小结:判断两圆位置关系的方法
1、圆心距与半径的比较→位置关系.
2、联立两圆方程→方程组解的情况→位置关系.
三、巩固新知
例2 已知圆的直径4,动点与点的距离是它与点的距离的倍.试探究点的轨迹,并判断该轨迹与圆的位置关系.
轨迹:符合一定规则的点集.
分析:利用坐标法求得轨迹方程,再进一步判断与圆的位置关系.
轨迹方程:点的坐标所满足的方程.
O
A
B
M
P
解:如图,以线段的中点为原点, 所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系.
由=4,得,.
设点,由= ,得
,
得 , 即=32.
所以点的轨迹是以 (6,2)为圆心,半径为的一个圆.
轨迹方程
轨迹
圆心距,
两圆的半径分别为=2, =,
- << + ,
所以有两个公共点,两圆相交.
追问1:如果把本例中的“ 倍”,改为“”,你能分析并解决这个问题吗?
设点,由= ,得
,
得 ,
当1时,点 的轨迹为的垂直平分线;
当1时,点 的轨迹为.
小结:坐标法求动点轨迹问题的基本步骤
第一步
建立适当的平面直角坐标系
寻找动点满足的几何关系
第二步
将几何问题用方程表示
代数化简、变形,得到轨迹方程
第二步
把轨迹方程“翻译”成轨迹
四、课堂小结
1、圆与圆的位置关系
五、作业布置
课本P95:练习 第1、2题
2、坐标法解题步骤
2.5.2
圆与圆的位置关系
人教A版(2019)选择性必修第一册
学习目标
1.能根据给定圆的方程,判断圆与圆的位置关系。
2.圆与圆位置关系的其判定方法。
3.用坐标法探求圆与圆位置关系的过程。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
圆与圆的位置关系
A.相离、相切、相交
B.外离、外切、相交、内切、内含
相离
两圆没有公共点
外离、内含
相切
两圆只有一个公共点
外切、内切
相交
两圆有两个公共点
相交
外离
外切
内切
内含
问题1 设两圆圆心之间的距离为,两圆半径分别为, ,则两圆的位置关系与, , 之间又什么联系?
二、新课讲授
1、圆与圆的位置关系
外切
= +
内切
= - 丨
相交
- 丨+
内切
= - 丨
内含
<- 丨
例1:已知圆,圆,试判断圆与圆的位置关系.
分析:
法1:可通过两圆心之间的距离与两半径之和或之差进行比较,得到两圆位置关系.
①需求出两圆心的坐标即两圆的半径;
②可将圆的方程化为标准方程.
法2:可通过两圆公共点的个数来判断两圆位置关系.
①联立两圆方程,解方程组;
②由方程组解的情况来判断位置关系.
解法一:圆的方程可化为: 的圆心为(-1,-4),半径5.
圆的方程可化为: 的圆心为(2,2),半径.
则= .
与圆的两半径之和为: + =5+
与圆的两半径之差为: - =5-
5- < < 5+ ,即- < < + ,
所以与圆有两个公共点,两圆相交.
解法二:将两圆方程联立,得
①-②,得
由=.代入①,并整理得:
因为方程的>0,所以方程有两个不相等的实数根, .
解得3, -1,分别代入方程③,解得-1, 1.
所以与圆有两个公共点,分别为(-1,1),(3,-1),两圆相交.
追问1:你能求出公共弦所在直线方程吗?
解:因为两圆的两个交点(-1,1),(3,-1)在公共弦上,
所以根据两点式可得公共弦所在直线的方程为:
追问2:方程与①-②得到方程一致,是巧合吗?
两圆相交时,公共弦所在直线方程就是两圆方程之差所得到的方程.
追问3:如果所求=0或<0,说明什么?
当=0时,方程只有一个实数解,即两圆只有一个公共点,故两圆内切或外切.
当<0时,方程没有实数解,即两圆没有公共点,故两圆内含或外离.
要想得到更确切的位置,还需要通过圆心距与两半径之和或之差进行比较来判断.
小结:判断两圆位置关系的方法
1、圆心距与半径的比较→位置关系.
2、联立两圆方程→方程组解的情况→位置关系.
三、巩固新知
例2 已知圆的直径4,动点与点的距离是它与点的距离的倍.试探究点的轨迹,并判断该轨迹与圆的位置关系.
轨迹:符合一定规则的点集.
分析:利用坐标法求得轨迹方程,再进一步判断与圆的位置关系.
轨迹方程:点的坐标所满足的方程.
O
A
B
M
P
解:如图,以线段的中点为原点, 所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系.
由=4,得,.
设点,由= ,得
,
得 , 即=32.
所以点的轨迹是以 (6,2)为圆心,半径为的一个圆.
轨迹方程
轨迹
圆心距,
两圆的半径分别为=2, =,
- << + ,
所以有两个公共点,两圆相交.
追问1:如果把本例中的“ 倍”,改为“”,你能分析并解决这个问题吗?
设点,由= ,得
,
得 ,
当1时,点 的轨迹为的垂直平分线;
当1时,点 的轨迹为.
小结:坐标法求动点轨迹问题的基本步骤
第一步
建立适当的平面直角坐标系
寻找动点满足的几何关系
第二步
将几何问题用方程表示
代数化简、变形,得到轨迹方程
第二步
把轨迹方程“翻译”成轨迹
四、课堂小结
1、圆与圆的位置关系
五、作业布置
课本P95:练习 第1、2题
2、坐标法解题步骤
