24.1.2 垂直于弦的直径(1)(浙江省台州市临海市)
文档属性
| 名称 | 24.1.2 垂直于弦的直径(1)(浙江省台州市临海市) |

|
|
| 格式 | rar | ||
| 文件大小 | 626.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-23 00:00:00 | ||
图片预览

文档简介
课件18张PPT。
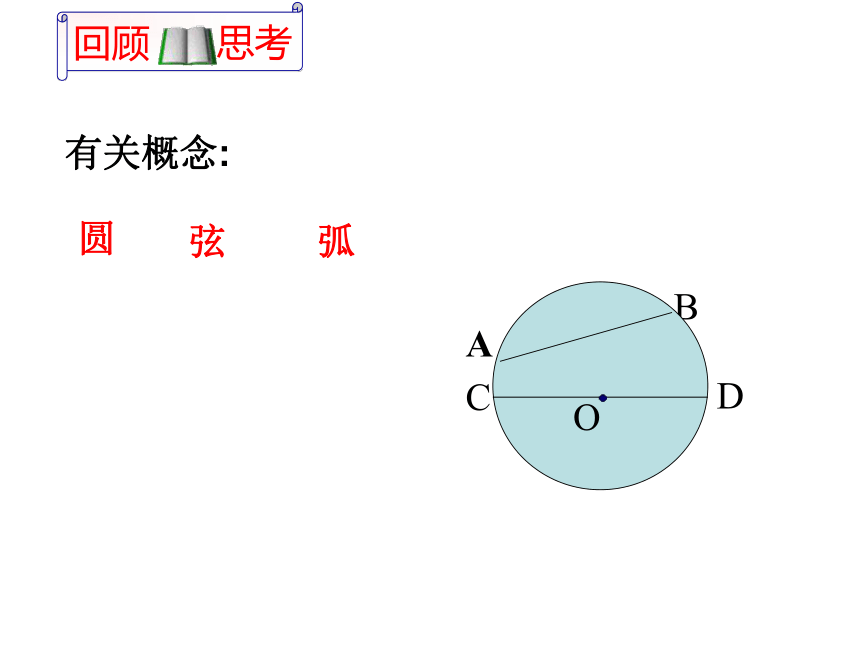
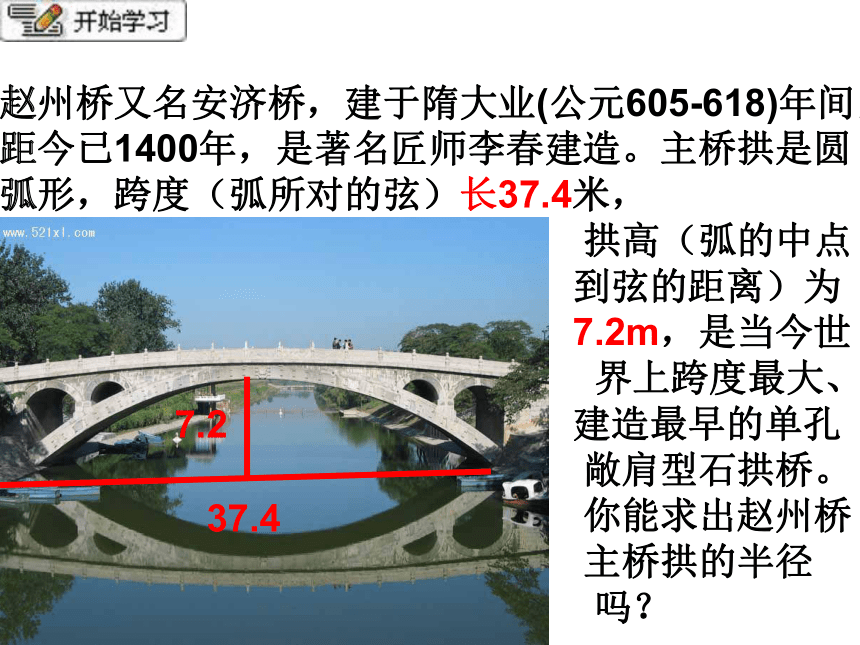
24.1.2 垂直于弦的直径(1)有关概念:圆弦弧 赵州桥又名安济桥,建于隋大业(公元605-618)年间,距今已1400年,是著名匠师李春建造。主桥拱是圆弧形,跨度(弧所对的弦)长37.4米,
拱高(弧的中点
到弦的距离)为
7.2m,是当今世
界上跨度最大、
建造最早的单孔
敞肩型石拱桥。
你能求出赵州桥
主桥拱的半径
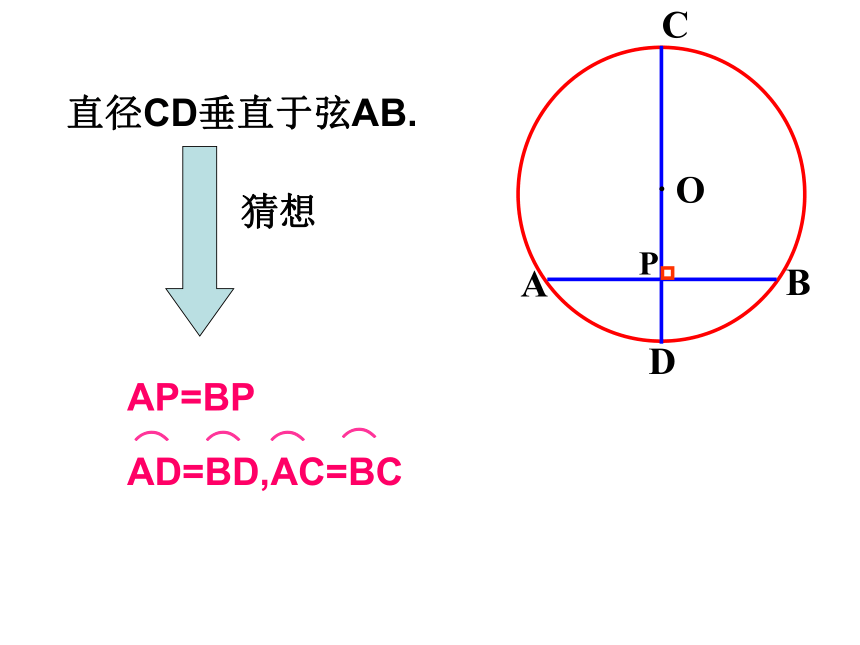
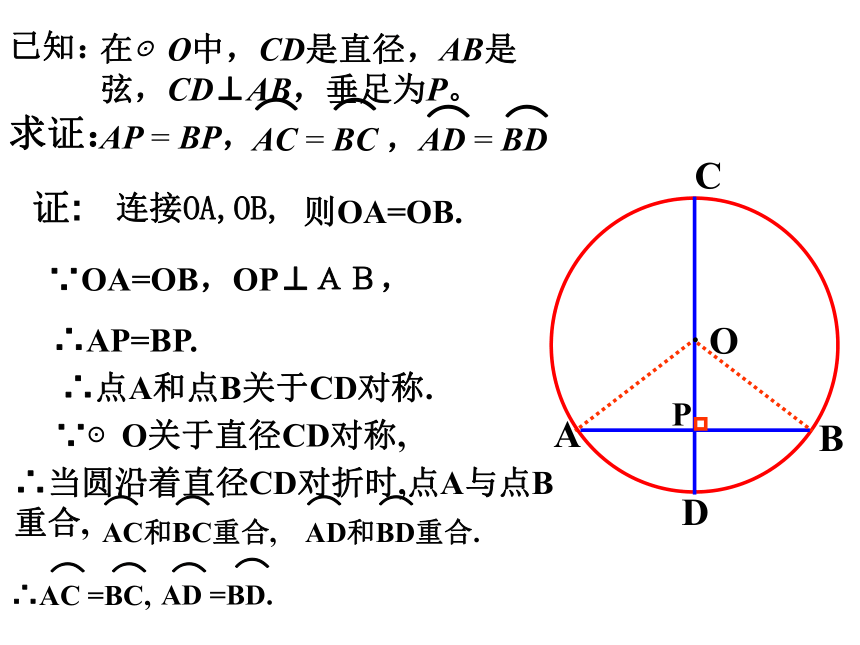
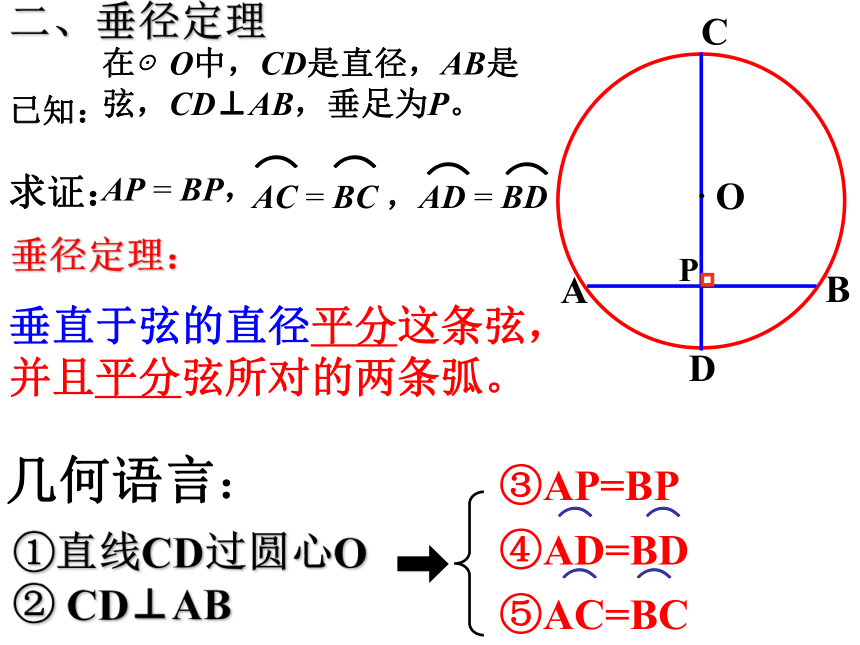
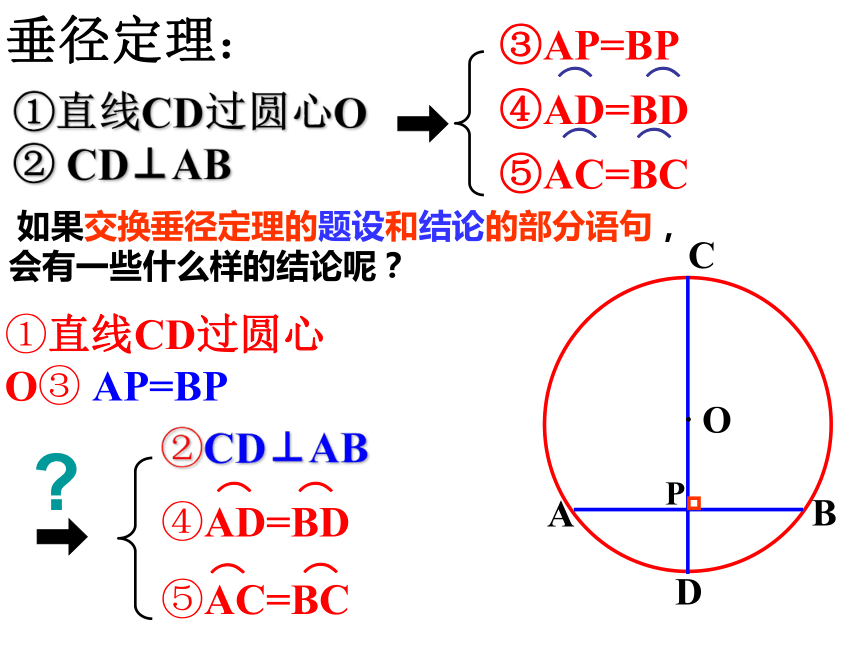
吗? 37.47.2·ABCDOP直径CD垂直于弦AB.猜想AP=BP·ABCDOPAP = BP,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。已知: 连接OA,OB,则OA=OB.∵OA=OB,OP⊥AB,∴AP=BP.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,证:AP = BP,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。已知:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:二、垂径定理·ABCDOP①直线CD过圆心O ② CD⊥AB几何语言:①直线CD过圆心O ② CD⊥AB垂径定理: 如果交换垂径定理的题设和结论的部分语句,会有一些什么样的结论呢?①直线CD过圆心O③ AP=BP
?①直线CD过圆心O③ AP=BP
条件结论垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 几何语言:例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. 变式一:在⊙O中,直径为10cm,弦AB的长为8cm,求圆心O 到AB的距离.变式二:在⊙O中,直径为10cm,圆心O 到AB的距离为3cm,求弦AB的长.思考:若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?练习:AB是⊙O的直径,弦CD⊥AB,E为垂足,若AE=9,BE=1,求CD的长.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________. 35 赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?问题?OABr某机械加工厂要把一个如图所示的破轮子重新加式成新的一个轮子,加工前先要在图纸上计算出这个破轮子所在圆的直径.
已知图中弦AB=40cm,高CD=10cm,请你帮助工人师傅求出该破轮的直径.ABCD练习: 例2.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。 CD20152525247CDFFAB、CD在点O两侧EF=OE+OF=15+7=22AB、CD在点O同侧EF=OE-OF=15-7=8过点O作直线OE⊥AB,交CD于F。例3. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
试说明:AC=BD。E.ACDBO证明:过O作OE⊥AB于E∵OE⊥AB∴AE=EB∵OE⊥CD∴CE=ED∴AE-CE=EB-ED即AC=BD应用2:垂径定理有关的证明题.AB耐心填一填:如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________. ·MOABNC2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
A. 3 B. 6 C. 9 D. 103. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.AC=BCA C⌒⌒0<x≤62或8·MNOAB图2图1C课堂小结请同学们谈谈你的收获-------
24.1.2 垂直于弦的直径(1)有关概念:圆弦弧 赵州桥又名安济桥,建于隋大业(公元605-618)年间,距今已1400年,是著名匠师李春建造。主桥拱是圆弧形,跨度(弧所对的弦)长37.4米,
拱高(弧的中点
到弦的距离)为
7.2m,是当今世
界上跨度最大、
建造最早的单孔
敞肩型石拱桥。
你能求出赵州桥
主桥拱的半径
吗? 37.47.2·ABCDOP直径CD垂直于弦AB.猜想AP=BP·ABCDOPAP = BP,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。已知: 连接OA,OB,则OA=OB.∵OA=OB,OP⊥AB,∴AP=BP.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,证:AP = BP,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。已知:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:二、垂径定理·ABCDOP①直线CD过圆心O ② CD⊥AB几何语言:①直线CD过圆心O ② CD⊥AB垂径定理: 如果交换垂径定理的题设和结论的部分语句,会有一些什么样的结论呢?①直线CD过圆心O③ AP=BP
?①直线CD过圆心O③ AP=BP
条件结论垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 几何语言:例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. 变式一:在⊙O中,直径为10cm,弦AB的长为8cm,求圆心O 到AB的距离.变式二:在⊙O中,直径为10cm,圆心O 到AB的距离为3cm,求弦AB的长.思考:若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?练习:AB是⊙O的直径,弦CD⊥AB,E为垂足,若AE=9,BE=1,求CD的长.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________. 35 赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?问题?OABr某机械加工厂要把一个如图所示的破轮子重新加式成新的一个轮子,加工前先要在图纸上计算出这个破轮子所在圆的直径.
已知图中弦AB=40cm,高CD=10cm,请你帮助工人师傅求出该破轮的直径.ABCD练习: 例2.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。 CD20152525247CDFFAB、CD在点O两侧EF=OE+OF=15+7=22AB、CD在点O同侧EF=OE-OF=15-7=8过点O作直线OE⊥AB,交CD于F。例3. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
试说明:AC=BD。E.ACDBO证明:过O作OE⊥AB于E∵OE⊥AB∴AE=EB∵OE⊥CD∴CE=ED∴AE-CE=EB-ED即AC=BD应用2:垂径定理有关的证明题.AB耐心填一填:如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________. ·MOABNC2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
A. 3 B. 6 C. 9 D. 103. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.AC=BCA C⌒⌒0<x≤62或8·MNOAB图2图1C课堂小结请同学们谈谈你的收获-------
同课章节目录
