24.1.2 垂直于弦的直径(2)(浙江省台州市临海市)
文档属性
| 名称 | 24.1.2 垂直于弦的直径(2)(浙江省台州市临海市) |  | |
| 格式 | rar | ||
| 文件大小 | 230.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-23 20:24:00 | ||
图片预览


文档简介
课件20张PPT。
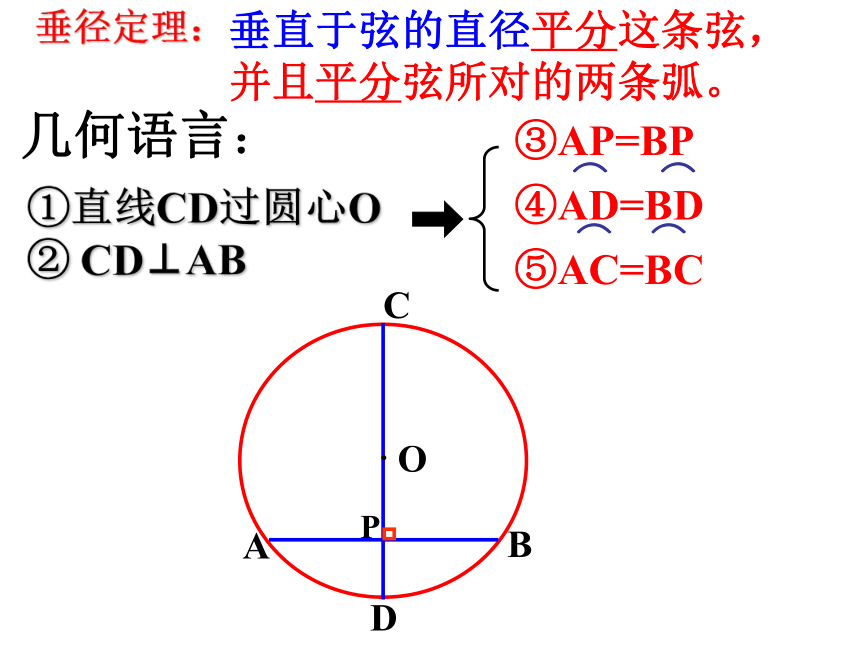
24.1.2 垂直于弦的直径(2)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:①直线CD过圆心O ② CD⊥AB几何语言:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 ①直线CD过圆心O③ AP=BP
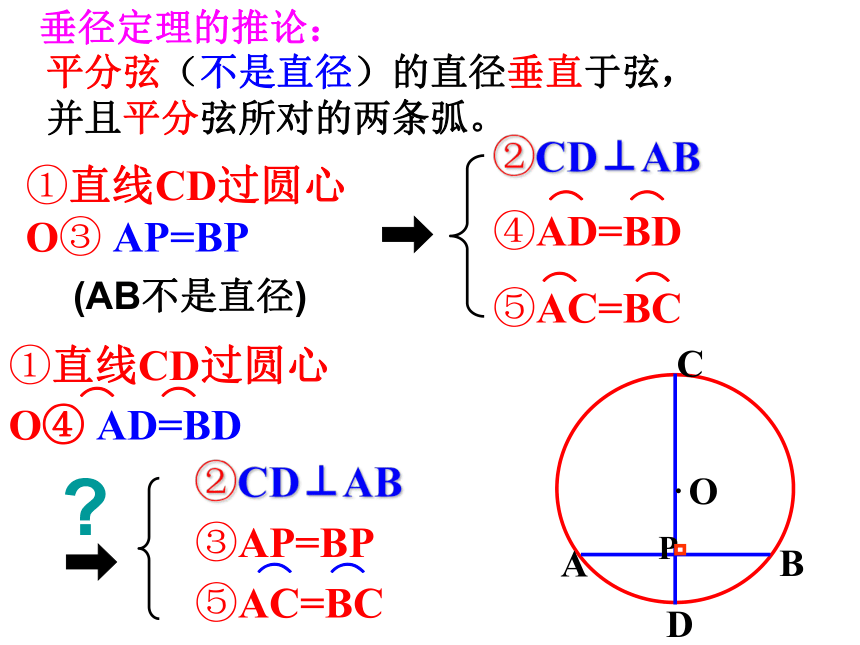
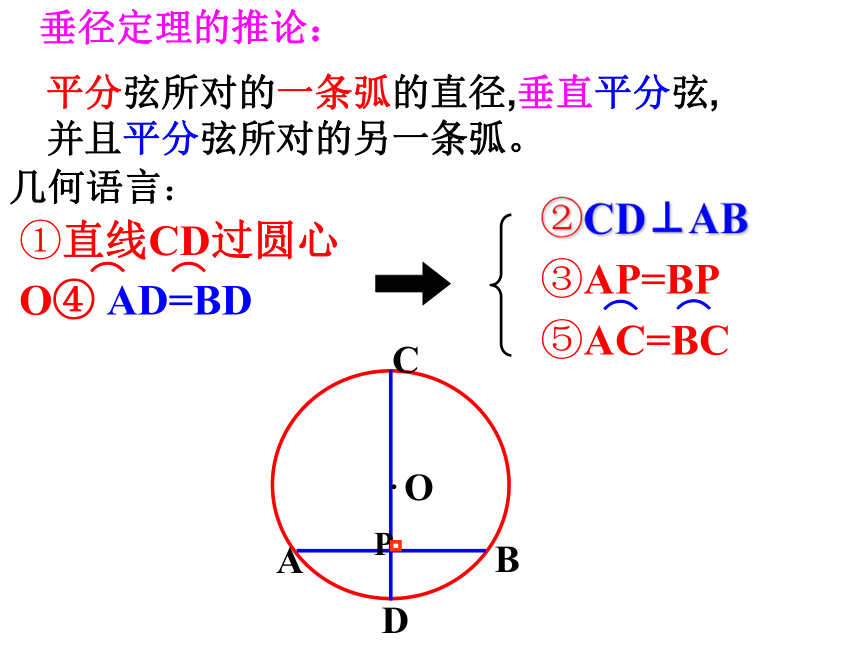
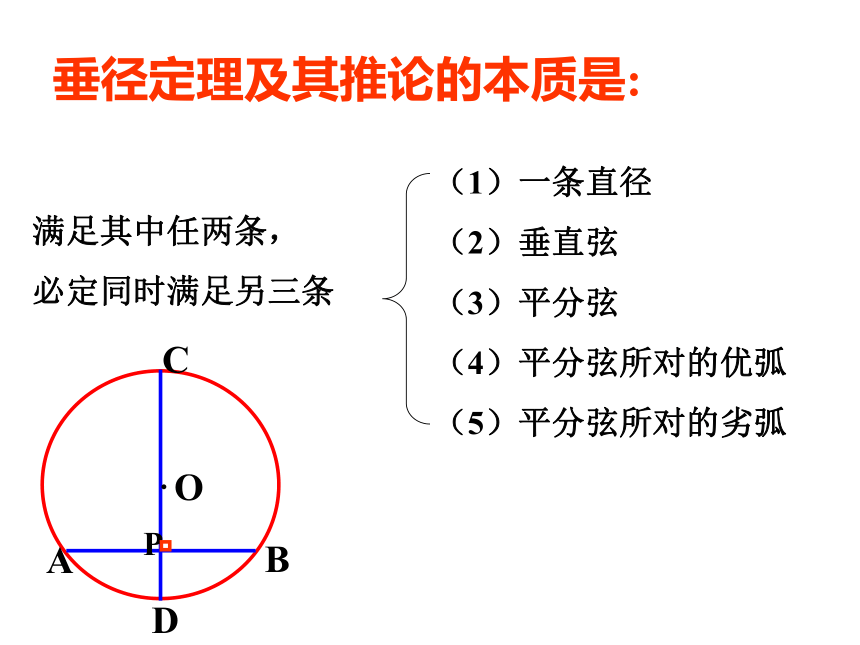
垂径定理的推论:(AB不是直径)?平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。垂径定理的推论:几何语言:垂径定理及其推论的本质是:满足其中任两条,
必定同时满足另三条(1)一条直径
(2)垂直弦
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
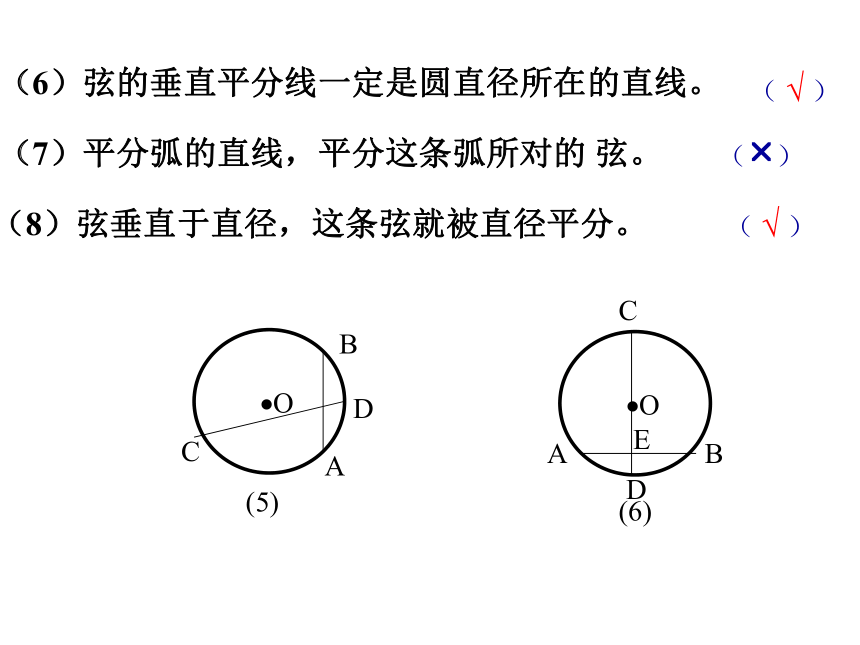
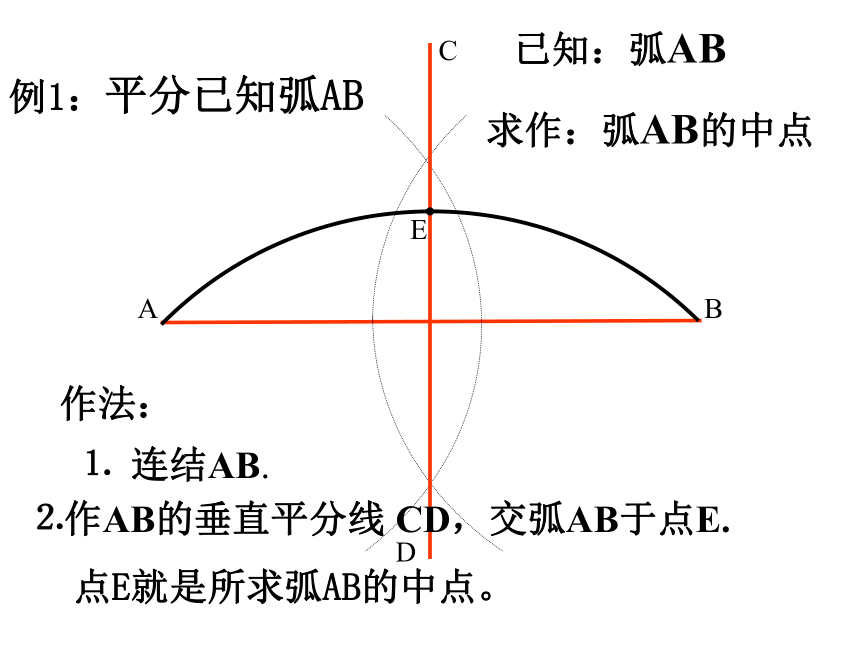
(1)垂直于弦的直线平分弦并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)圆的不与直径垂直的弦必不被这条直径平分…………………………………………...( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )(5)圆内两条非直径的弦不能互相平分( )×√××√(6)弦的垂直平分线一定是圆直径所在的直线。(7)平分弧的直线,平分这条弧所对的 弦。(8)弦垂直于直径,这条弦就被直径平分。( √ )(?)( √ )9如图,在⊙CDABE例1:平分已知弧AB已知:弧AB作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点CDABEFG变式一: 求弧AB的四等分点。 mn变式二:你能确定 弧AB的圆心吗?CABMO 例2.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。 CD20152525247CDFFAB、CD在点O两侧EF=OE+OF=15+7=22AB、CD在点O同侧EF=OE-OF=15-7=8过点O作直线OE⊥AB,交CD于F。例3. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
试说明:AC=BD。E.ACDBO证明:过O作OE⊥AB于E∵OE⊥AB∴AE=EB∵OE⊥CD∴CE=ED∴AE-CE=EB-ED即AC=BD应用2:垂径定理有关的证明题.船能过拱桥吗如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?ADOFCENBHMr垂径定理的逆应用在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. DC耐心填一填:如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________. ·MOABNC2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
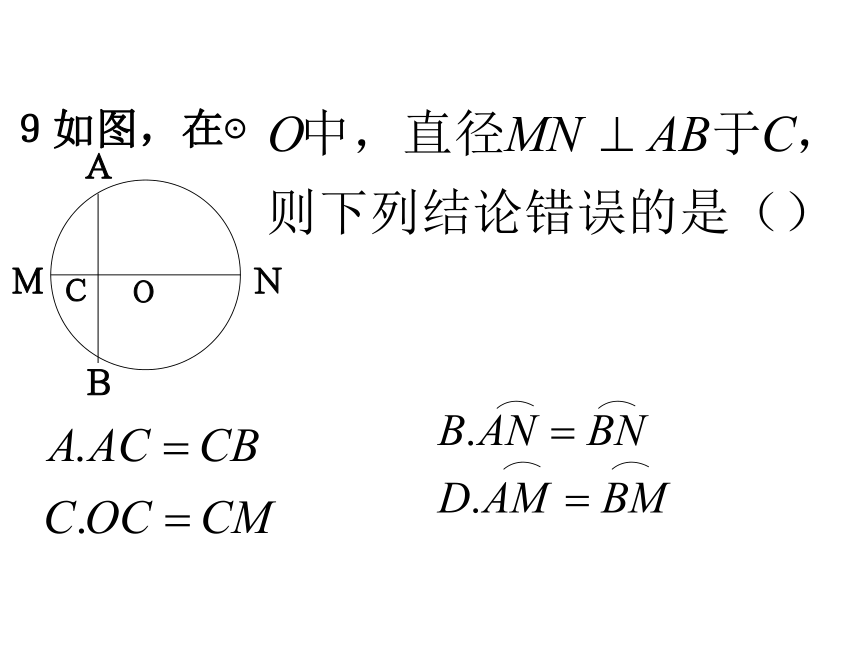
A. 3 B. 6 C. 9 D. 103. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.AC=BCA C⌒⌒0<x≤62或8·MNOAB图2图1C挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.例:求证:圆的两条平行弦所夹的弧相等..AEBOCD.AEBOCDFCODEF
24.1.2 垂直于弦的直径(2)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:①直线CD过圆心O ② CD⊥AB几何语言:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 ①直线CD过圆心O③ AP=BP
垂径定理的推论:(AB不是直径)?平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。垂径定理的推论:几何语言:垂径定理及其推论的本质是:满足其中任两条,
必定同时满足另三条(1)一条直径
(2)垂直弦
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
(1)垂直于弦的直线平分弦并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)圆的不与直径垂直的弦必不被这条直径平分…………………………………………...( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )(5)圆内两条非直径的弦不能互相平分( )×√××√(6)弦的垂直平分线一定是圆直径所在的直线。(7)平分弧的直线,平分这条弧所对的 弦。(8)弦垂直于直径,这条弦就被直径平分。( √ )(?)( √ )9如图,在⊙CDABE例1:平分已知弧AB已知:弧AB作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点CDABEFG变式一: 求弧AB的四等分点。 mn变式二:你能确定 弧AB的圆心吗?CABMO 例2.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。 CD20152525247CDFFAB、CD在点O两侧EF=OE+OF=15+7=22AB、CD在点O同侧EF=OE-OF=15-7=8过点O作直线OE⊥AB,交CD于F。例3. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
试说明:AC=BD。E.ACDBO证明:过O作OE⊥AB于E∵OE⊥AB∴AE=EB∵OE⊥CD∴CE=ED∴AE-CE=EB-ED即AC=BD应用2:垂径定理有关的证明题.船能过拱桥吗如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?ADOFCENBHMr垂径定理的逆应用在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. DC耐心填一填:如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________. ·MOABNC2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
A. 3 B. 6 C. 9 D. 103. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.AC=BCA C⌒⌒0<x≤62或8·MNOAB图2图1C挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.例:求证:圆的两条平行弦所夹的弧相等..AEBOCD.AEBOCDFCODEF
同课章节目录
