5.2.2函数的表示方法 第2课时《分段函数》讲义(含答案)
文档属性
| 名称 | 5.2.2函数的表示方法 第2课时《分段函数》讲义(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 656.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 14:04:51 | ||
图片预览




文档简介
编号:026 课题: §5.2.2 函数的表示方法——第2课时 分段函数
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.会作出分段函数的图象;
2.会根据分段函数的图象进行求值或求范围;
3.理解并掌握分段函数的表示方法及应用;
4.理解并掌握分段函数在实际问题中的应用.
本节重点难点
重点:分段函数的表示方法及应用;
难点:分段函数在实际问题中的应用.
学科素养目标
函数是“通过建立数学模型来刻画与研究世界”的典范,也是学习数学和研究数学的范例.学习“函数概念与基本初等函数I”(下面简称“函数” )这一章,从观念上认识“函数” ,它是“语言、工具、应用”.它挑起了“万水千山”(整个高中数学),贯通了数学世界,迎接着广泛的实际问题.认识函数,就是认识它是解决许多实际问题的基本模型;认识函数,在于研究它的性质;认识函数,应明了它的根本价值在于应用,并揭示了它的“生长性”即如许许多多对数据都统一于一个函数式.
通过本章的学习,逐步培养学生的数学思维,养成准确、清晰、有条理地表述问题以及问题的解决过程的习惯,形成、提高数学表达和交流的能力,逐步地发展独立获取数学知识的能力,发展数学应用意识和创新意识,提高学习数学的兴趣,树立学好数学的信心,形成锲而不舍的钻研精神和科学态度,进一步拓宽学生的数学视野,逐步认识数学的科学价值、应用价值和文化价值,形成批判性的思维习惯,崇尚数学的理性精神.
教学过程
基础知识积累
1. 分段函数
(1)定义:在定义域内不同部分上,有不同的 ,像这样的函数叫作分段函数.
(2)本质:函数在定义域的不同的范围内,有着不同的对应关系.
(3)应用:可以用分段函数描述很多生活中的实际问题.
【思考】
1.分段函数是两个函数吗
2.分段函数的定义域、值域是怎么规定的
【课前小题演练】
题1.函数y=+x的图象是( )
题2.已知f(x)=则f(f(f(-2)))等于( )
A.π B.0 C.2 D.π+1
题3.函数f(x)=x2-2|x|的图象是( )
题4.设函数f(x)=则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞)
B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞)
D.(-∞,-3)∪(1,3)
题5.函数f(x)=的值域是( )
A.R B.[0,2]∪{3} C.[0,+∞) D.[0,3]
题6.已知函数f=,则不等式f≥2x的解集是( )
A. B.(-∞,0]
C. D.(-∞,2)
题7(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是( )
A.f(x)=x- B.f(x)=x+
C.f(x)= D.f(x)=
题8(多选题).已知函数f=若f=2,则实数a的值为( )
A.-2 B.- C.-1 D.1
题9(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是 ( )
A.f(x)=x- B.f(x)=x+ C.f(x)= D.f(x)=
题10.已知函数f(x)=,则不等式f(x)≤x的解集为________.
题11.已知函数f(x)=则f(1)=________,若f(f(0))=a,则实数a=________.
题12.已知函数f(x)=
(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
【课堂题组训练】
题13.已知函数f(x)=关于函数f(x)的结论正确的是( )
A.f(x)的定义域为R
B.f(x)<1的解集为(-1,1)
C.f(1)=3
D.若f(x)=3,则x的值是
题14.已知f(x)=则f(x)的图象大致为( )
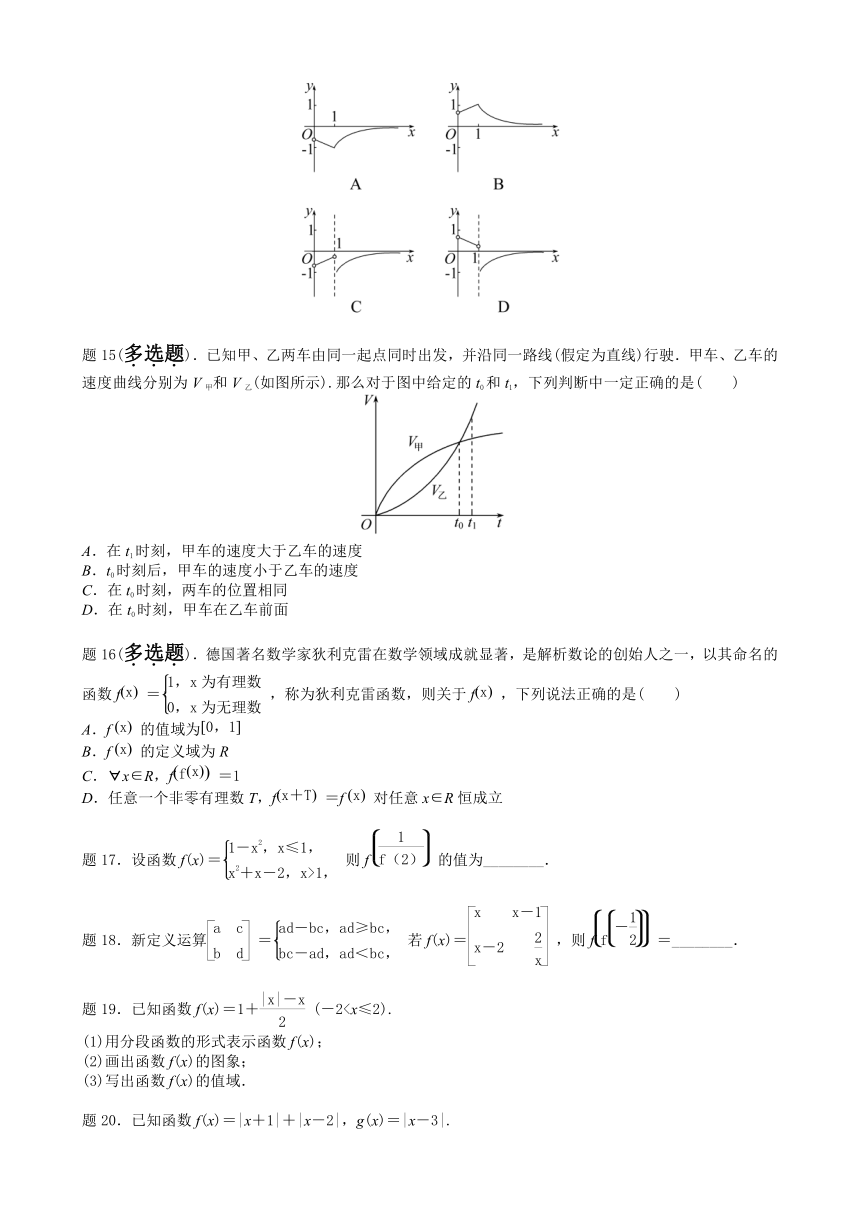
题15(多选题).已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
题16(多选题).德国著名数学家狄利克雷在数学领域成就显著,是解析数论的创始人之一,以其命名的函数f=,称为狄利克雷函数,则关于f,下列说法正确的是( )
A.f的值域为
B.f的定义域为R
C. x∈R,f=1
D.任意一个非零有理数T,f=f对任意x∈R恒成立
题17.设函数f(x)=则f的值为________.
题18.新定义运算=若f(x)=,则f=________.
题19.已知函数f(x)=1+(-2(1)用分段函数的形式表示函数f(x);
(2)画出函数f(x)的图象;
(3)写出函数f(x)的值域.
题20.已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2) x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
【综合突破拔高】
题21.函数f(x)=|x-1|的图象是( )
题22.已知f(x)=使f(x)≥-1成立的x的取值范围是( )
A.[-4,2) B.[-4,2] C.(0,2] D.(-4,2]
题23.设f(x)=则f(5)的值为( )
A.10 B.11 C.12 D.13
题24.已知函数f(x)=,若n>m且f(n)=f(m),设t=n-m,则( )
A.t没有最小值 B.t的最小值为-1
C.t的最小值为 D.t的最小值为
题25.在股票买卖过程中,经常用到两种曲线:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x).例如,f(2)=3是指开始买卖2小时的即时价格为3元;g(2)=3是指开始买卖2小时内的平均价格为3元.如图给出的四个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
题26.在自然数集N上定义的函数f(n)=则f(90)的值是( )
A.997 B.998 C.999 D.1 000
题27(多选题)已知f(x)=,g(x)=,则( )
A.f=-9 B.g=9
C.f=-3 D.g=-81
题28(多选题).设函数f(x)=若f(a)=4,则实数a的值可以是( )
A.-4 B.2 C.-2 D.4
题29(多选题).已知f(x)=,则f(x)满足的关系有 ( )
A.f(-x)=-f(x) B.f=-f(x) C.f=f(x) D.f=-f(x)
题30(多选题).已知某超市2020年12个月的收入与支出数据的折线图如图所示:
根据该折线图可知,下列说法正确的是 ( )
A.该超市2020年的12个月中的7月份的收益最高
B.该超市2020年的12个月中的4月份的收益最低
C.该超市2020年1~6月份的总收益低于2020年7~12月份的总收益
D.该超市2020年7~12月份的总收益比2020年1~6月份的总收益增长了90万元
题31(多选题).为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是 ( )
A.当x∈[0,2)时有害垃圾错误分类的重量加速增长
B.当x∈[2,4)时有害垃圾错误分类的重量匀速增长
C.当x∈[4,6)时有害垃圾错误分类的重量相对于当x∈[2,4)时增长了30%
D.当x∈[6,8]时有害垃圾错误分类的重量相对于当x∈[0,2)时减少了1.6吨
题32.函数f(x)的图象如图所示,则函数f(x)=__________.
题33.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域为
________.
题34.已知函数f(x)的图象如图所示,求f(x)的解析式.
题35.已知函数f(x)=
(1)求f的值;
(2)若f(x)=,求x的值.
编号:026 课题: §5.2.2 函数的表示方法——第2课时 分段函数
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.会作出分段函数的图象;
2.会根据分段函数的图象进行求值或求范围;
3.理解并掌握分段函数的表示方法及应用;
4.理解并掌握分段函数在实际问题中的应用.
本节重点难点
重点:分段函数的表示方法及应用;
难点:分段函数在实际问题中的应用.
学科素养目标
函数是“通过建立数学模型来刻画与研究世界”的典范,也是学习数学和研究数学的范例.学习“函数概念与基本初等函数I”(下面简称“函数” )这一章,从观念上认识“函数” ,它是“语言、工具、应用”.它挑起了“万水千山”(整个高中数学),贯通了数学世界,迎接着广泛的实际问题.认识函数,就是认识它是解决许多实际问题的基本模型;认识函数,在于研究它的性质;认识函数,应明了它的根本价值在于应用,并揭示了它的“生长性”即如许许多多对数据都统一于一个函数式.
通过本章的学习,逐步培养学生的数学思维,养成准确、清晰、有条理地表述问题以及问题的解决过程的习惯,形成、提高数学表达和交流的能力,逐步地发展独立获取数学知识的能力,发展数学应用意识和创新意识,提高学习数学的兴趣,树立学好数学的信心,形成锲而不舍的钻研精神和科学态度,进一步拓宽学生的数学视野,逐步认识数学的科学价值、应用价值和文化价值,形成批判性的思维习惯,崇尚数学的理性精神.
教学过程
基础知识积累
1. 分段函数
(1)定义:在定义域内不同部分上,有不同的 解析表达式 ,像这样的函数叫作分段函数.
(2)本质:函数在定义域的不同的范围内,有着不同的对应关系.
(3)应用:可以用分段函数描述很多生活中的实际问题.
【思考】
1.分段函数是两个函数吗
提示:分段函数是一个函数,只不过在不同范围上解析式不同.
2.分段函数的定义域、值域是怎么规定的
提示:定义域为各段范围的并集;值域为各段上值域的并集.
【课前小题演练】
题1.函数y=+x的图象是( )
【解析】选C.因为函数y=+x=,由一次函数的图象知选项C正确.
题2.已知f(x)=则f(f(f(-2)))等于( )
A.π B.0 C.2 D.π+1
【解析】选D.因为-2<0,所以f(-2)=0,所以f(f(-2))=f(0)=π,因为π>0,
所以f(f(f(-2)))=f(π)=π+1.
题3.函数f(x)=x2-2|x|的图象是( )
【解析】选C.f(x)=分段画出其图象,如选项C中所示.
题4.设函数f(x)=则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞)
B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞)
D.(-∞,-3)∪(1,3)
【解析】选A.f(1)=12-4×1+6=3,当x≥0时,x2-4x+6>3,解得x>3或0≤x<1;
当x<0时,x+6>3,解得-3f(1)的解集是(-3,1)∪(3,+∞).
题5.函数f(x)=的值域是( )
A.R B.[0,2]∪{3} C.[0,+∞) D.[0,3]
【解析】选B.当0≤x≤1时,0≤2x≤2,
即0≤f(x)≤2;当1当x≥2时,f(x)=3.
综上可知f(x)的值域为[0,2]∪{3}.
题6.已知函数f=,则不等式f≥2x的解集是( )
A. B.(-∞,0]
C. D.(-∞,2)
【解析】选A.当x>0时,f=-x+2≥2x,解得3x≤2,所以0当x≤0时,f=x+2≥2x,解得x≤2,又x≤0,所以x≤0.
综上,原不等式的解集为.
题7(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是( )
A.f(x)=x- B.f(x)=x+
C.f(x)= D.f(x)=
【解析】选ACD.对于A,f(x)=x-,f=-x=-f(x),满足;
对于B,f=+x=f(x),不满足;
对于C,f=
即f=
故f=-f(x),满足.
对于D,因为f===-f(x),满足.
综上可知,满足“倒负”变换的函数是ACD.
题8(多选题).已知函数f=若f=2,则实数a的值为( )
A.-2 B.- C.-1 D.1
【解析】选AB.令f=t,故f=2,进而得t=-1或t=1,所以f=-1或f=1,由于x>0时f≥2,所以3a+5=-1或3a+5=1,解得a=-2或a=-.
题9(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是 ( )
A.f(x)=x- B.f(x)=x+ C.f(x)= D.f(x)=
【解析】选ACD.
对于A,f(x)=x-,f=-x=-f(x),满足;对于B,f=+x=f(x),不满足;
对于C,f=即f=故f=-f(x),满足.
对于D,因为f===-f(x),所以满足.
综上可知,满足“倒负”变换的函数是ACD.
题10.已知函数f(x)=,则不等式f(x)≤x的解集为________.
【解析】当x≥0时,f(x)=x2-2x≤x,解得0≤x≤3;
当x<0时,f(x)=≤x,解得-1≤x<0,
综上,不等式f(x)≤x的解集为[-1,3].
答案:[-1,3]
题11.已知函数f(x)=则f(1)=________,若f(f(0))=a,则实数a=________.
【解析】依题意知f(1)=3+2=5;f(0)=3×0+2=2,
则f(f(0))=f(2)=22-2a=a,求得a=.
答案:5
题12.已知函数f(x)=
(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
【解析】(1)由分段函数可知,函数f(x)的简图为:
(2)因为f(3)=4-32=4-9=-5,
所以f(f(3))=f(-5)=1-2×(-5)=1+10=11.
(3)当-4≤x<0时,1<f(x)≤9;
当x=0时,f(0)=2;
当0<x<3时,-5<f(x)<4,
综上,当-4≤x<3时,f(x)取值的集合为(-5,9].
【课堂题组训练】
题13.已知函数f(x)=关于函数f(x)的结论正确的是( )
A.f(x)的定义域为R
B.f(x)<1的解集为(-1,1)
C.f(1)=3
D.若f(x)=3,则x的值是
【解析】选D.由题意知函数f(x)的定义域为(-∞,2),故A错误;
当x≤-1时,x+2<1,解得x<-1,
当-1因此f(x)<1的解集为(-∞,-1)∪(-1,1),故B错误;
当x=1时,f(1)=12=1,故C错误;
当x≤-1时,x+2=3,解得x=1(舍去),
当-1题14.已知f(x)=则f(x)的图象大致为( )
【解析】选A.由f(1)=-1<0,排除选项B,C,D.
题15(多选题).已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
【解析】选BD.由题图可知,当时间为t1时,甲车的速度小于乙车的速度;t0时刻之前,甲车的速度一直大于乙车,时间相同的情况下,甲车行驶路程大于乙车行驶路程,故t0时刻甲车在乙车前面;t0时刻后,甲车的速度小于乙车的速度.
题16(多选题).德国著名数学家狄利克雷在数学领域成就显著,是解析数论的创始人之一,以其命名的函数f=,称为狄利克雷函数,则关于f,下列说法正确的是( )
A.f的值域为
B.f的定义域为R
C. x∈R,f=1
D.任意一个非零有理数T,f=f对任意x∈R恒成立
【解析】选BCD.因为函数f=,所以f的值域为,故A不正确;
因为函数f=,所以f的定义域为R,故B正确;
因为 x∈R,f∈,所以f=1,故C正确;
对于任意一个非零有理数T,若x是有理数,则x+T是有理数;
若x是无理数,则x+T是无理数,根据函数的解析式,任取一个不为零的有理数T,都有f=f对任意x∈R恒成立,故D正确.
题17.设函数f(x)=则f的值为________.
【解析】因为函数f(x)=2>1,
所以f(2)=22+2-2=4,
则f=f=1-=.
答案:
题18.新定义运算=若f(x)=,则f=________.
【解析】由题意知f(x)=
且x≠0,
所以f(x)=
所以f=,
所以f=f=.
答案:
题19.已知函数f(x)=1+(-2(1)用分段函数的形式表示函数f(x);
(2)画出函数f(x)的图象;
(3)写出函数f(x)的值域.
【解析】(1)当0≤x≤2时,
f(x)=1+=1,
当-2<x<0时,
f(x)=1+=1-x.
所以f(x)=
(2)函数f(x)的图象如图所示.
(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).
题20.已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2) x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
【解析】(1)f(x)=
g(x)=
则对应的图象如图:
(2)min(x)图象如图:
解析式为min(x)=
(3)若f(x)>g(x),
则由图象知在A点左侧,B点右侧满足条件.
此时对应的x满足x>0或x<-2,即不等式f(x)>g(x)的解集为(-∞,-2)∪(0,+∞).
【综合突破拔高】
题21.函数f(x)=|x-1|的图象是( )
【解析】选B.方法一:函数的解析式可化为y=画出此分段函数的图象.
方法二:由f(-1)=2,知图象过点(-1,2),排除A,C,D.
题22.已知f(x)=使f(x)≥-1成立的x的取值范围是( )
A.[-4,2) B.[-4,2] C.(0,2] D.(-4,2]
【解析】选B.因为f(x)≥-1,所以或
所以-4≤x≤0或0<x≤2,即-4≤x≤2.
题23.设f(x)=则f(5)的值为( )
A.10 B.11 C.12 D.13
【解析】选B.因为f(x)=
所以f(5)=f(f(11))=f(9)=f(f(15))=f(13)=11.
题24.已知函数f(x)=,若n>m且f(n)=f(m),设t=n-m,则( )
A.t没有最小值 B.t的最小值为-1
C.t的最小值为 D.t的最小值为
【解析】选B.如图,作出函数f(x)的图象.
因为f(n)=f(m)且n>m,则m≤1且n>1,
所以3m+1=n2-1即m=.
由,解得1所以n-m=n-=-(n2-3n-2)=-+.
又因为1题25.在股票买卖过程中,经常用到两种曲线:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x).例如,f(2)=3是指开始买卖2小时的即时价格为3元;g(2)=3是指开始买卖2小时内的平均价格为3元.如图给出的四个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
【解析】选A.开始时平均价格与即时价格一致,排除C,D,即时价格减少时,平均价格不可能增大,排除B.
题26.在自然数集N上定义的函数f(n)=则f(90)的值是( )
A.997 B.998 C.999 D.1 000
【解析】选A.n<1 000时,有f(n)=f(n+7),所以f(90)=f(97)=f(104)=…=f(1 000)=1 000-3=997.
题27(多选题)已知f(x)=,g(x)=,则( )
A.f=-9 B.g=9
C.f=-3 D.g=-81
【解析】选ACD.
f=f=-9,g=g(-3)=-9,
f=f(-3)=-3,g=g=-81.
题28(多选题).设函数f(x)=若f(a)=4,则实数a的值可以是( )
A.-4 B.2 C.-2 D.4
【解析】选AB.当a≤0时,f(a)=-a=4,解得a=-4;当a>0时,f(a)=a2=4,解得a=±2.
因为a>0,所以a=2,综上a=-4或2.
题29(多选题).已知f(x)=,则f(x)满足的关系有 ( )
A.f(-x)=-f(x) B.f=-f(x) C.f=f(x) D.f=-f(x)
【解析】选BD.因为f(x)=,所以f(-x)==,f(-x)=f(x),
即不满足A选项,f==,f=-f(x),即满足B选项,不满足C选项,
f==,f=-f(x),即满足D选项.
题30(多选题).已知某超市2020年12个月的收入与支出数据的折线图如图所示:
根据该折线图可知,下列说法正确的是 ( )
A.该超市2020年的12个月中的7月份的收益最高
B.该超市2020年的12个月中的4月份的收益最低
C.该超市2020年1~6月份的总收益低于2020年7~12月份的总收益
D.该超市2020年7~12月份的总收益比2020年1~6月份的总收益增长了90万元
【解析】选ABC.经计算该超市2020年的12个月中的7月份的收益最高,故A正确;该超市2020年的12个月中的4月份的收益最低,故B正确;该超市2020年1~6月份的总收益为20+30+20+10+30+30=140(万元),2020年7~12月份的总收益为60+40+30+30+50+30=240(万元),故C正确;由240-140=100(万元),故D错误.
题31(多选题).为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是 ( )
A.当x∈[0,2)时有害垃圾错误分类的重量加速增长
B.当x∈[2,4)时有害垃圾错误分类的重量匀速增长
C.当x∈[4,6)时有害垃圾错误分类的重量相对于当x∈[2,4)时增长了30%
D.当x∈[6,8]时有害垃圾错误分类的重量相对于当x∈[0,2)时减少了1.6吨
【解析】选AB.由统计图可知,第2周增长数量比第1周增长数量明显要多,所以是加速增长,
所以选项A正确;
当x∈[2,4)时图象是线段,所以是匀速增长,所以选项B正确;
当x∈[4,6)时增长数量比当x∈[2,4)时增长数量要少,所以是减少,所以选项C错误;
当x∈[0,2)时共增长2.4吨,当x∈[6,8]时共增长0.6吨,所以减少了1.8吨,所以选项D不正确.
题32.函数f(x)的图象如图所示,则函数f(x)=__________.
【思路导引】由图象确定函数类型,待定系数法求解析式.
【解析】当x<-1时,设f(x)=ax+b,
则解得所以f(x)=x+2;
当-1≤x≤2时,设f(x)=kx2,由4=k·22得k=1,所以f(x)=x2;
当x>2时,设f(x)=cx+d,则
解得所以f(x)=2x,所以f(x)=
答案:
题33.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域为________.
【解析】由题意得f(x)=画出函数f(x)的图象得值域是(-∞,1].
答案:(-∞,1]
题34.已知函数f(x)的图象如图所示,求f(x)的解析式.
【解析】由题图可知,图象是由两条线段组成,当-1≤x<0时,设f(x)=ax+b,将(-1,0),(0,1)代入解析式,则所以当0≤x≤1时,设f(x)=kx,将(1,-1)代入,则k=-1.
故f(x)=
题35.已知函数f(x)=
(1)求f的值;
(2)若f(x)=,求x的值.
【解析】(1)因为f=-2=-,
所以f=f==.
(2)f(x)=,若|x|≤1,则|x-1|-2=,得x=或x=-.
因为|x|≤1,所以x的值不存在;若|x|>1,则=,得x=±,符合|x|>1.所以若f(x)=,x的值为±.
- 0 -
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.会作出分段函数的图象;
2.会根据分段函数的图象进行求值或求范围;
3.理解并掌握分段函数的表示方法及应用;
4.理解并掌握分段函数在实际问题中的应用.
本节重点难点
重点:分段函数的表示方法及应用;
难点:分段函数在实际问题中的应用.
学科素养目标
函数是“通过建立数学模型来刻画与研究世界”的典范,也是学习数学和研究数学的范例.学习“函数概念与基本初等函数I”(下面简称“函数” )这一章,从观念上认识“函数” ,它是“语言、工具、应用”.它挑起了“万水千山”(整个高中数学),贯通了数学世界,迎接着广泛的实际问题.认识函数,就是认识它是解决许多实际问题的基本模型;认识函数,在于研究它的性质;认识函数,应明了它的根本价值在于应用,并揭示了它的“生长性”即如许许多多对数据都统一于一个函数式.
通过本章的学习,逐步培养学生的数学思维,养成准确、清晰、有条理地表述问题以及问题的解决过程的习惯,形成、提高数学表达和交流的能力,逐步地发展独立获取数学知识的能力,发展数学应用意识和创新意识,提高学习数学的兴趣,树立学好数学的信心,形成锲而不舍的钻研精神和科学态度,进一步拓宽学生的数学视野,逐步认识数学的科学价值、应用价值和文化价值,形成批判性的思维习惯,崇尚数学的理性精神.
教学过程
基础知识积累
1. 分段函数
(1)定义:在定义域内不同部分上,有不同的 ,像这样的函数叫作分段函数.
(2)本质:函数在定义域的不同的范围内,有着不同的对应关系.
(3)应用:可以用分段函数描述很多生活中的实际问题.
【思考】
1.分段函数是两个函数吗
2.分段函数的定义域、值域是怎么规定的
【课前小题演练】
题1.函数y=+x的图象是( )
题2.已知f(x)=则f(f(f(-2)))等于( )
A.π B.0 C.2 D.π+1
题3.函数f(x)=x2-2|x|的图象是( )
题4.设函数f(x)=则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞)
B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞)
D.(-∞,-3)∪(1,3)
题5.函数f(x)=的值域是( )
A.R B.[0,2]∪{3} C.[0,+∞) D.[0,3]
题6.已知函数f=,则不等式f≥2x的解集是( )
A. B.(-∞,0]
C. D.(-∞,2)
题7(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是( )
A.f(x)=x- B.f(x)=x+
C.f(x)= D.f(x)=
题8(多选题).已知函数f=若f=2,则实数a的值为( )
A.-2 B.- C.-1 D.1
题9(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是 ( )
A.f(x)=x- B.f(x)=x+ C.f(x)= D.f(x)=
题10.已知函数f(x)=,则不等式f(x)≤x的解集为________.
题11.已知函数f(x)=则f(1)=________,若f(f(0))=a,则实数a=________.
题12.已知函数f(x)=
(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
【课堂题组训练】
题13.已知函数f(x)=关于函数f(x)的结论正确的是( )
A.f(x)的定义域为R
B.f(x)<1的解集为(-1,1)
C.f(1)=3
D.若f(x)=3,则x的值是
题14.已知f(x)=则f(x)的图象大致为( )
题15(多选题).已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
题16(多选题).德国著名数学家狄利克雷在数学领域成就显著,是解析数论的创始人之一,以其命名的函数f=,称为狄利克雷函数,则关于f,下列说法正确的是( )
A.f的值域为
B.f的定义域为R
C. x∈R,f=1
D.任意一个非零有理数T,f=f对任意x∈R恒成立
题17.设函数f(x)=则f的值为________.
题18.新定义运算=若f(x)=,则f=________.
题19.已知函数f(x)=1+(-2
(2)画出函数f(x)的图象;
(3)写出函数f(x)的值域.
题20.已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2) x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
【综合突破拔高】
题21.函数f(x)=|x-1|的图象是( )
题22.已知f(x)=使f(x)≥-1成立的x的取值范围是( )
A.[-4,2) B.[-4,2] C.(0,2] D.(-4,2]
题23.设f(x)=则f(5)的值为( )
A.10 B.11 C.12 D.13
题24.已知函数f(x)=,若n>m且f(n)=f(m),设t=n-m,则( )
A.t没有最小值 B.t的最小值为-1
C.t的最小值为 D.t的最小值为
题25.在股票买卖过程中,经常用到两种曲线:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x).例如,f(2)=3是指开始买卖2小时的即时价格为3元;g(2)=3是指开始买卖2小时内的平均价格为3元.如图给出的四个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
题26.在自然数集N上定义的函数f(n)=则f(90)的值是( )
A.997 B.998 C.999 D.1 000
题27(多选题)已知f(x)=,g(x)=,则( )
A.f=-9 B.g=9
C.f=-3 D.g=-81
题28(多选题).设函数f(x)=若f(a)=4,则实数a的值可以是( )
A.-4 B.2 C.-2 D.4
题29(多选题).已知f(x)=,则f(x)满足的关系有 ( )
A.f(-x)=-f(x) B.f=-f(x) C.f=f(x) D.f=-f(x)
题30(多选题).已知某超市2020年12个月的收入与支出数据的折线图如图所示:
根据该折线图可知,下列说法正确的是 ( )
A.该超市2020年的12个月中的7月份的收益最高
B.该超市2020年的12个月中的4月份的收益最低
C.该超市2020年1~6月份的总收益低于2020年7~12月份的总收益
D.该超市2020年7~12月份的总收益比2020年1~6月份的总收益增长了90万元
题31(多选题).为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是 ( )
A.当x∈[0,2)时有害垃圾错误分类的重量加速增长
B.当x∈[2,4)时有害垃圾错误分类的重量匀速增长
C.当x∈[4,6)时有害垃圾错误分类的重量相对于当x∈[2,4)时增长了30%
D.当x∈[6,8]时有害垃圾错误分类的重量相对于当x∈[0,2)时减少了1.6吨
题32.函数f(x)的图象如图所示,则函数f(x)=__________.
题33.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域为
________.
题34.已知函数f(x)的图象如图所示,求f(x)的解析式.
题35.已知函数f(x)=
(1)求f的值;
(2)若f(x)=,求x的值.
编号:026 课题: §5.2.2 函数的表示方法——第2课时 分段函数
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.会作出分段函数的图象;
2.会根据分段函数的图象进行求值或求范围;
3.理解并掌握分段函数的表示方法及应用;
4.理解并掌握分段函数在实际问题中的应用.
本节重点难点
重点:分段函数的表示方法及应用;
难点:分段函数在实际问题中的应用.
学科素养目标
函数是“通过建立数学模型来刻画与研究世界”的典范,也是学习数学和研究数学的范例.学习“函数概念与基本初等函数I”(下面简称“函数” )这一章,从观念上认识“函数” ,它是“语言、工具、应用”.它挑起了“万水千山”(整个高中数学),贯通了数学世界,迎接着广泛的实际问题.认识函数,就是认识它是解决许多实际问题的基本模型;认识函数,在于研究它的性质;认识函数,应明了它的根本价值在于应用,并揭示了它的“生长性”即如许许多多对数据都统一于一个函数式.
通过本章的学习,逐步培养学生的数学思维,养成准确、清晰、有条理地表述问题以及问题的解决过程的习惯,形成、提高数学表达和交流的能力,逐步地发展独立获取数学知识的能力,发展数学应用意识和创新意识,提高学习数学的兴趣,树立学好数学的信心,形成锲而不舍的钻研精神和科学态度,进一步拓宽学生的数学视野,逐步认识数学的科学价值、应用价值和文化价值,形成批判性的思维习惯,崇尚数学的理性精神.
教学过程
基础知识积累
1. 分段函数
(1)定义:在定义域内不同部分上,有不同的 解析表达式 ,像这样的函数叫作分段函数.
(2)本质:函数在定义域的不同的范围内,有着不同的对应关系.
(3)应用:可以用分段函数描述很多生活中的实际问题.
【思考】
1.分段函数是两个函数吗
提示:分段函数是一个函数,只不过在不同范围上解析式不同.
2.分段函数的定义域、值域是怎么规定的
提示:定义域为各段范围的并集;值域为各段上值域的并集.
【课前小题演练】
题1.函数y=+x的图象是( )
【解析】选C.因为函数y=+x=,由一次函数的图象知选项C正确.
题2.已知f(x)=则f(f(f(-2)))等于( )
A.π B.0 C.2 D.π+1
【解析】选D.因为-2<0,所以f(-2)=0,所以f(f(-2))=f(0)=π,因为π>0,
所以f(f(f(-2)))=f(π)=π+1.
题3.函数f(x)=x2-2|x|的图象是( )
【解析】选C.f(x)=分段画出其图象,如选项C中所示.
题4.设函数f(x)=则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞)
B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞)
D.(-∞,-3)∪(1,3)
【解析】选A.f(1)=12-4×1+6=3,当x≥0时,x2-4x+6>3,解得x>3或0≤x<1;
当x<0时,x+6>3,解得-3
题5.函数f(x)=的值域是( )
A.R B.[0,2]∪{3} C.[0,+∞) D.[0,3]
【解析】选B.当0≤x≤1时,0≤2x≤2,
即0≤f(x)≤2;当1
综上可知f(x)的值域为[0,2]∪{3}.
题6.已知函数f=,则不等式f≥2x的解集是( )
A. B.(-∞,0]
C. D.(-∞,2)
【解析】选A.当x>0时,f=-x+2≥2x,解得3x≤2,所以0
综上,原不等式的解集为.
题7(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是( )
A.f(x)=x- B.f(x)=x+
C.f(x)= D.f(x)=
【解析】选ACD.对于A,f(x)=x-,f=-x=-f(x),满足;
对于B,f=+x=f(x),不满足;
对于C,f=
即f=
故f=-f(x),满足.
对于D,因为f===-f(x),满足.
综上可知,满足“倒负”变换的函数是ACD.
题8(多选题).已知函数f=若f=2,则实数a的值为( )
A.-2 B.- C.-1 D.1
【解析】选AB.令f=t,故f=2,进而得t=-1或t=1,所以f=-1或f=1,由于x>0时f≥2,所以3a+5=-1或3a+5=1,解得a=-2或a=-.
题9(多选题).已知具有性质:f=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是 ( )
A.f(x)=x- B.f(x)=x+ C.f(x)= D.f(x)=
【解析】选ACD.
对于A,f(x)=x-,f=-x=-f(x),满足;对于B,f=+x=f(x),不满足;
对于C,f=即f=故f=-f(x),满足.
对于D,因为f===-f(x),所以满足.
综上可知,满足“倒负”变换的函数是ACD.
题10.已知函数f(x)=,则不等式f(x)≤x的解集为________.
【解析】当x≥0时,f(x)=x2-2x≤x,解得0≤x≤3;
当x<0时,f(x)=≤x,解得-1≤x<0,
综上,不等式f(x)≤x的解集为[-1,3].
答案:[-1,3]
题11.已知函数f(x)=则f(1)=________,若f(f(0))=a,则实数a=________.
【解析】依题意知f(1)=3+2=5;f(0)=3×0+2=2,
则f(f(0))=f(2)=22-2a=a,求得a=.
答案:5
题12.已知函数f(x)=
(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
【解析】(1)由分段函数可知,函数f(x)的简图为:
(2)因为f(3)=4-32=4-9=-5,
所以f(f(3))=f(-5)=1-2×(-5)=1+10=11.
(3)当-4≤x<0时,1<f(x)≤9;
当x=0时,f(0)=2;
当0<x<3时,-5<f(x)<4,
综上,当-4≤x<3时,f(x)取值的集合为(-5,9].
【课堂题组训练】
题13.已知函数f(x)=关于函数f(x)的结论正确的是( )
A.f(x)的定义域为R
B.f(x)<1的解集为(-1,1)
C.f(1)=3
D.若f(x)=3,则x的值是
【解析】选D.由题意知函数f(x)的定义域为(-∞,2),故A错误;
当x≤-1时,x+2<1,解得x<-1,
当-1
当x=1时,f(1)=12=1,故C错误;
当x≤-1时,x+2=3,解得x=1(舍去),
当-1
【解析】选A.由f(1)=-1<0,排除选项B,C,D.
题15(多选题).已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
【解析】选BD.由题图可知,当时间为t1时,甲车的速度小于乙车的速度;t0时刻之前,甲车的速度一直大于乙车,时间相同的情况下,甲车行驶路程大于乙车行驶路程,故t0时刻甲车在乙车前面;t0时刻后,甲车的速度小于乙车的速度.
题16(多选题).德国著名数学家狄利克雷在数学领域成就显著,是解析数论的创始人之一,以其命名的函数f=,称为狄利克雷函数,则关于f,下列说法正确的是( )
A.f的值域为
B.f的定义域为R
C. x∈R,f=1
D.任意一个非零有理数T,f=f对任意x∈R恒成立
【解析】选BCD.因为函数f=,所以f的值域为,故A不正确;
因为函数f=,所以f的定义域为R,故B正确;
因为 x∈R,f∈,所以f=1,故C正确;
对于任意一个非零有理数T,若x是有理数,则x+T是有理数;
若x是无理数,则x+T是无理数,根据函数的解析式,任取一个不为零的有理数T,都有f=f对任意x∈R恒成立,故D正确.
题17.设函数f(x)=则f的值为________.
【解析】因为函数f(x)=2>1,
所以f(2)=22+2-2=4,
则f=f=1-=.
答案:
题18.新定义运算=若f(x)=,则f=________.
【解析】由题意知f(x)=
且x≠0,
所以f(x)=
所以f=,
所以f=f=.
答案:
题19.已知函数f(x)=1+(-2
(2)画出函数f(x)的图象;
(3)写出函数f(x)的值域.
【解析】(1)当0≤x≤2时,
f(x)=1+=1,
当-2<x<0时,
f(x)=1+=1-x.
所以f(x)=
(2)函数f(x)的图象如图所示.
(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).
题20.已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2) x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
【解析】(1)f(x)=
g(x)=
则对应的图象如图:
(2)min(x)图象如图:
解析式为min(x)=
(3)若f(x)>g(x),
则由图象知在A点左侧,B点右侧满足条件.
此时对应的x满足x>0或x<-2,即不等式f(x)>g(x)的解集为(-∞,-2)∪(0,+∞).
【综合突破拔高】
题21.函数f(x)=|x-1|的图象是( )
【解析】选B.方法一:函数的解析式可化为y=画出此分段函数的图象.
方法二:由f(-1)=2,知图象过点(-1,2),排除A,C,D.
题22.已知f(x)=使f(x)≥-1成立的x的取值范围是( )
A.[-4,2) B.[-4,2] C.(0,2] D.(-4,2]
【解析】选B.因为f(x)≥-1,所以或
所以-4≤x≤0或0<x≤2,即-4≤x≤2.
题23.设f(x)=则f(5)的值为( )
A.10 B.11 C.12 D.13
【解析】选B.因为f(x)=
所以f(5)=f(f(11))=f(9)=f(f(15))=f(13)=11.
题24.已知函数f(x)=,若n>m且f(n)=f(m),设t=n-m,则( )
A.t没有最小值 B.t的最小值为-1
C.t的最小值为 D.t的最小值为
【解析】选B.如图,作出函数f(x)的图象.
因为f(n)=f(m)且n>m,则m≤1且n>1,
所以3m+1=n2-1即m=.
由,解得1
又因为1
【解析】选A.开始时平均价格与即时价格一致,排除C,D,即时价格减少时,平均价格不可能增大,排除B.
题26.在自然数集N上定义的函数f(n)=则f(90)的值是( )
A.997 B.998 C.999 D.1 000
【解析】选A.n<1 000时,有f(n)=f(n+7),所以f(90)=f(97)=f(104)=…=f(1 000)=1 000-3=997.
题27(多选题)已知f(x)=,g(x)=,则( )
A.f=-9 B.g=9
C.f=-3 D.g=-81
【解析】选ACD.
f=f=-9,g=g(-3)=-9,
f=f(-3)=-3,g=g=-81.
题28(多选题).设函数f(x)=若f(a)=4,则实数a的值可以是( )
A.-4 B.2 C.-2 D.4
【解析】选AB.当a≤0时,f(a)=-a=4,解得a=-4;当a>0时,f(a)=a2=4,解得a=±2.
因为a>0,所以a=2,综上a=-4或2.
题29(多选题).已知f(x)=,则f(x)满足的关系有 ( )
A.f(-x)=-f(x) B.f=-f(x) C.f=f(x) D.f=-f(x)
【解析】选BD.因为f(x)=,所以f(-x)==,f(-x)=f(x),
即不满足A选项,f==,f=-f(x),即满足B选项,不满足C选项,
f==,f=-f(x),即满足D选项.
题30(多选题).已知某超市2020年12个月的收入与支出数据的折线图如图所示:
根据该折线图可知,下列说法正确的是 ( )
A.该超市2020年的12个月中的7月份的收益最高
B.该超市2020年的12个月中的4月份的收益最低
C.该超市2020年1~6月份的总收益低于2020年7~12月份的总收益
D.该超市2020年7~12月份的总收益比2020年1~6月份的总收益增长了90万元
【解析】选ABC.经计算该超市2020年的12个月中的7月份的收益最高,故A正确;该超市2020年的12个月中的4月份的收益最低,故B正确;该超市2020年1~6月份的总收益为20+30+20+10+30+30=140(万元),2020年7~12月份的总收益为60+40+30+30+50+30=240(万元),故C正确;由240-140=100(万元),故D错误.
题31(多选题).为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是 ( )
A.当x∈[0,2)时有害垃圾错误分类的重量加速增长
B.当x∈[2,4)时有害垃圾错误分类的重量匀速增长
C.当x∈[4,6)时有害垃圾错误分类的重量相对于当x∈[2,4)时增长了30%
D.当x∈[6,8]时有害垃圾错误分类的重量相对于当x∈[0,2)时减少了1.6吨
【解析】选AB.由统计图可知,第2周增长数量比第1周增长数量明显要多,所以是加速增长,
所以选项A正确;
当x∈[2,4)时图象是线段,所以是匀速增长,所以选项B正确;
当x∈[4,6)时增长数量比当x∈[2,4)时增长数量要少,所以是减少,所以选项C错误;
当x∈[0,2)时共增长2.4吨,当x∈[6,8]时共增长0.6吨,所以减少了1.8吨,所以选项D不正确.
题32.函数f(x)的图象如图所示,则函数f(x)=__________.
【思路导引】由图象确定函数类型,待定系数法求解析式.
【解析】当x<-1时,设f(x)=ax+b,
则解得所以f(x)=x+2;
当-1≤x≤2时,设f(x)=kx2,由4=k·22得k=1,所以f(x)=x2;
当x>2时,设f(x)=cx+d,则
解得所以f(x)=2x,所以f(x)=
答案:
题33.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域为________.
【解析】由题意得f(x)=画出函数f(x)的图象得值域是(-∞,1].
答案:(-∞,1]
题34.已知函数f(x)的图象如图所示,求f(x)的解析式.
【解析】由题图可知,图象是由两条线段组成,当-1≤x<0时,设f(x)=ax+b,将(-1,0),(0,1)代入解析式,则所以当0≤x≤1时,设f(x)=kx,将(1,-1)代入,则k=-1.
故f(x)=
题35.已知函数f(x)=
(1)求f的值;
(2)若f(x)=,求x的值.
【解析】(1)因为f=-2=-,
所以f=f==.
(2)f(x)=,若|x|≤1,则|x-1|-2=,得x=或x=-.
因为|x|≤1,所以x的值不存在;若|x|>1,则=,得x=±,符合|x|>1.所以若f(x)=,x的值为±.
- 0 -
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
