24.2.1 点与圆的位置关系(2)(浙江省台州市临海市)
文档属性
| 名称 | 24.2.1 点与圆的位置关系(2)(浙江省台州市临海市) |  | |
| 格式 | rar | ||
| 文件大小 | 510.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-23 20:29:00 | ||
图片预览






文档简介
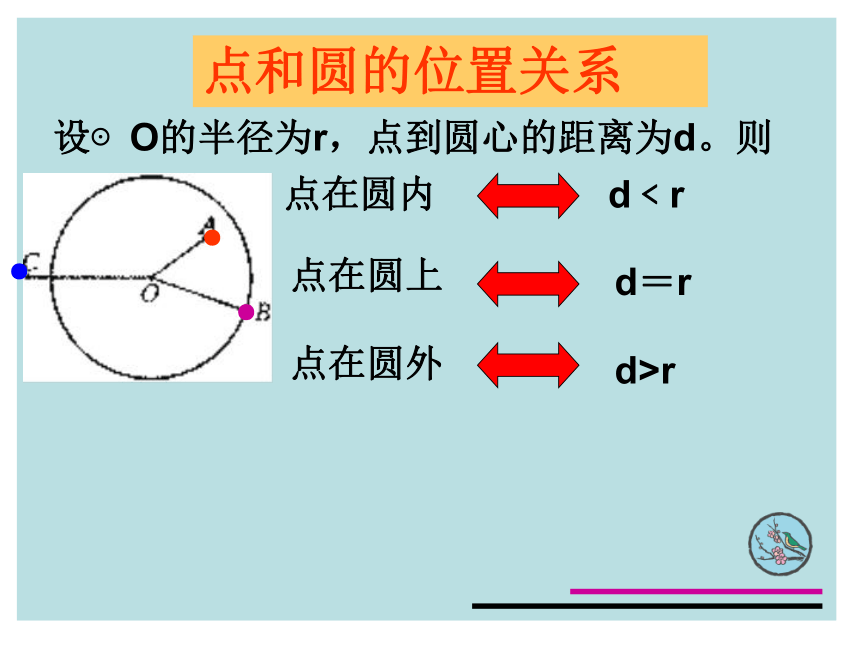
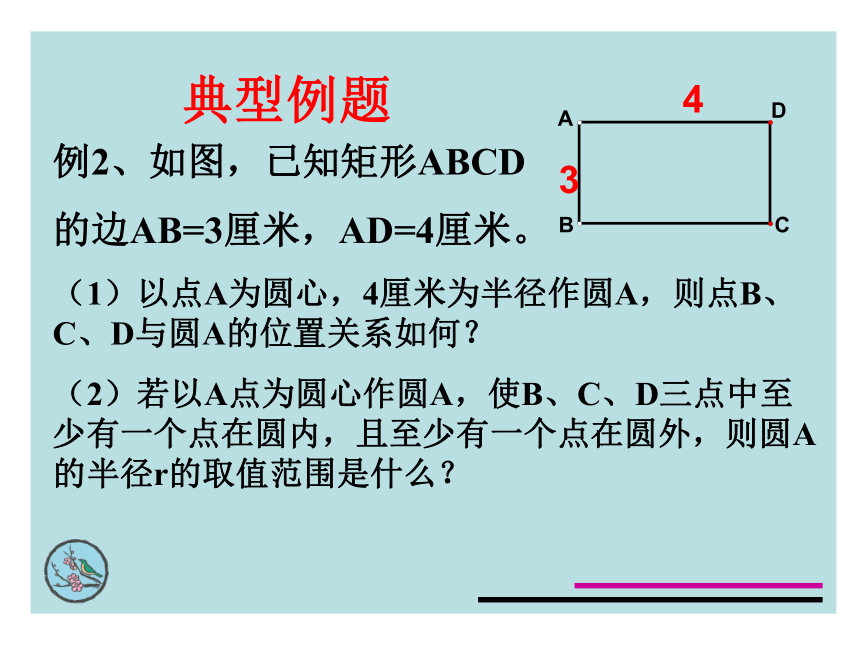
课件21张PPT。24.2.1点与圆的位置关系(2)设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r●●●典型例题例2、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?341.P为⊙O内与O不重合的一点,则下列说法正确的是( )
A.点P到⊙O上任一点的距离都小于⊙O的半径
B.⊙O上有两点到点P的距离等于⊙O的半径
C.⊙O上有两点到点P的距离最小
D.⊙O上有两点到点P的距离最大3.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这圆的半径是 cm.2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,则点P到⊙O上各点的最小距离是 .4.⊙A的半径为5,圆心A的坐标为(0,0),点P的坐标为(4,2),则点P与⊙A的位置关系( )
A.点P在⊙A内 B.点P在⊙A上
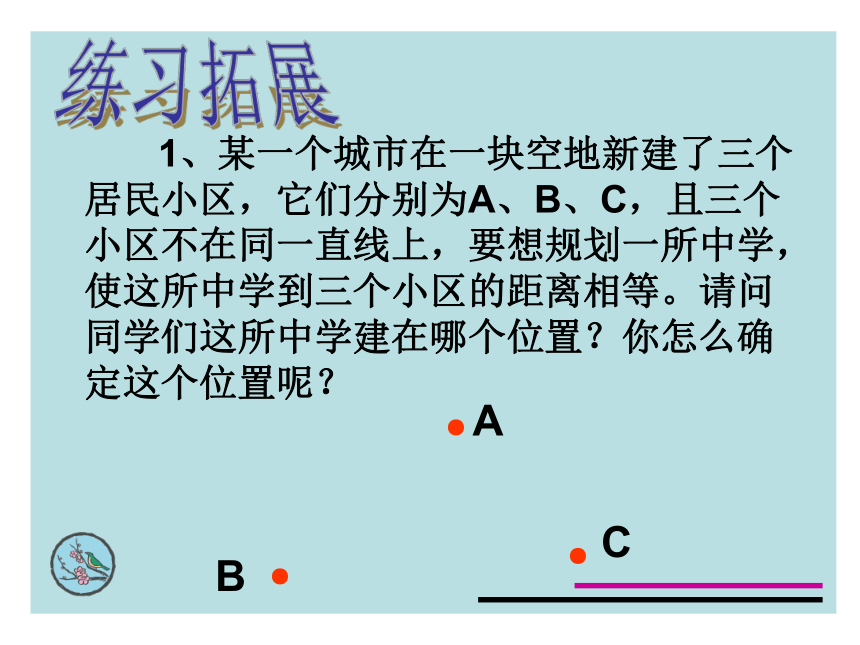
C.点P在⊙A外 D.点P在⊙A上或⊙A外(3,4)(5,8) 一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?定理:不在同一直线上的三个点确定一个圆。 1、某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?●●●BAC练习拓展2.已知线段AB和直线L,过A,B两点作圆,并使圆心在L上.问:
(1)当L∥AB时,可作几个这样的圆;
(2)当L与AB斜交时,可作几个这样的圆;
(3)当L垂直于AB且不过AB的中点时,可作几个这样的圆;
(4)当L是AB的垂直平分线时,可作几个这样的圆.2.思考题
①过三角形的三个顶点是否都可以作圆?为什么?
②一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
③三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。外心:(1)作法:任意两边垂直平分线的交点;
(2)性质:它到三角形三顶点的距离相等。判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、等腰三角形的外心一定在这个三角形内。( )×√××1.已知△ABC中,AC=15,BC=8,AB=17,求△ABC外接圆半径.2.已知△ABC中, ABAC=AC=10,BC=12,求△ABC外接圆半径.3.如果直角三角形的两条直角边分别是6,8,你能求出这个直角三角形的外接圆的半径吗?是多少?思考:经过同一条直线上的三个点能作出一个圆吗?从命题结论的反面出发,引出矛盾,从而证明原命题成立,这样的证明方法叫做反证法。反证法证题的步骤 (1)假设命题的结论不成立,即假设结论的反面成立;
(2)从假设出发,经过推理,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.例:求证:三角形中至少有一个内角不大于60度.已知如图, △ABC中,D,E两点分别在AB和AC上,求证:CD,BE不能互相平分.1、用否定的形式填空: (1)a > 0; 练习:(2)a、b都是正数;a≤0。a、b不都是正数。一般什么时候,适合用反证法?(1)结论本身是以否定形式出现的。
如:证明“不可能……”,“没有……”,“不存在……”等等。(2)有关结论是以“至多……”、“至少……”的形式出 现的命题。(3)关于唯一性、存在性的问题。(4)结论的反面比原结论更具体,更简单容易的命题。例题讲解例1 在△ABC中,若∠C是直角,那么∠B一定是锐角.证明 假设∠B是直角,
因∠C是直角,
所以∠C+∠B=180°,
此时∠A=0°,这与ABC为三角形矛盾,
所以∠B为锐角.思考:上述证明推理完整吗?1.想一想:
图中工具的CD边所在的直线恰好垂直平分
AB边,怎样用这个工具找出一个圆的圆心?
思考题:
1.经过四个点是不是一定能作圆?所以经过四点不一定能作圆。4、 1、如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 巩固新知 应用新知正确答案大家快算算!对吗?
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?341.P为⊙O内与O不重合的一点,则下列说法正确的是( )
A.点P到⊙O上任一点的距离都小于⊙O的半径
B.⊙O上有两点到点P的距离等于⊙O的半径
C.⊙O上有两点到点P的距离最小
D.⊙O上有两点到点P的距离最大3.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这圆的半径是 cm.2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,则点P到⊙O上各点的最小距离是 .4.⊙A的半径为5,圆心A的坐标为(0,0),点P的坐标为(4,2),则点P与⊙A的位置关系( )
A.点P在⊙A内 B.点P在⊙A上
C.点P在⊙A外 D.点P在⊙A上或⊙A外(3,4)(5,8) 一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?定理:不在同一直线上的三个点确定一个圆。 1、某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?●●●BAC练习拓展2.已知线段AB和直线L,过A,B两点作圆,并使圆心在L上.问:
(1)当L∥AB时,可作几个这样的圆;
(2)当L与AB斜交时,可作几个这样的圆;
(3)当L垂直于AB且不过AB的中点时,可作几个这样的圆;
(4)当L是AB的垂直平分线时,可作几个这样的圆.2.思考题
①过三角形的三个顶点是否都可以作圆?为什么?
②一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
③三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。外心:(1)作法:任意两边垂直平分线的交点;
(2)性质:它到三角形三顶点的距离相等。判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、等腰三角形的外心一定在这个三角形内。( )×√××1.已知△ABC中,AC=15,BC=8,AB=17,求△ABC外接圆半径.2.已知△ABC中, ABAC=AC=10,BC=12,求△ABC外接圆半径.3.如果直角三角形的两条直角边分别是6,8,你能求出这个直角三角形的外接圆的半径吗?是多少?思考:经过同一条直线上的三个点能作出一个圆吗?从命题结论的反面出发,引出矛盾,从而证明原命题成立,这样的证明方法叫做反证法。反证法证题的步骤 (1)假设命题的结论不成立,即假设结论的反面成立;
(2)从假设出发,经过推理,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.例:求证:三角形中至少有一个内角不大于60度.已知如图, △ABC中,D,E两点分别在AB和AC上,求证:CD,BE不能互相平分.1、用否定的形式填空: (1)a > 0; 练习:(2)a、b都是正数;a≤0。a、b不都是正数。一般什么时候,适合用反证法?(1)结论本身是以否定形式出现的。
如:证明“不可能……”,“没有……”,“不存在……”等等。(2)有关结论是以“至多……”、“至少……”的形式出 现的命题。(3)关于唯一性、存在性的问题。(4)结论的反面比原结论更具体,更简单容易的命题。例题讲解例1 在△ABC中,若∠C是直角,那么∠B一定是锐角.证明 假设∠B是直角,
因∠C是直角,
所以∠C+∠B=180°,
此时∠A=0°,这与ABC为三角形矛盾,
所以∠B为锐角.思考:上述证明推理完整吗?1.想一想:
图中工具的CD边所在的直线恰好垂直平分
AB边,怎样用这个工具找出一个圆的圆心?
思考题:
1.经过四个点是不是一定能作圆?所以经过四点不一定能作圆。4、 1、如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 巩固新知 应用新知正确答案大家快算算!对吗?
同课章节目录
