24.2.2 直线与圆的位置关系(2)(浙江省台州市临海市)
文档属性
| 名称 | 24.2.2 直线与圆的位置关系(2)(浙江省台州市临海市) |
|
|
| 格式 | rar | ||
| 文件大小 | 36.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-23 00:00:00 | ||
图片预览


文档简介
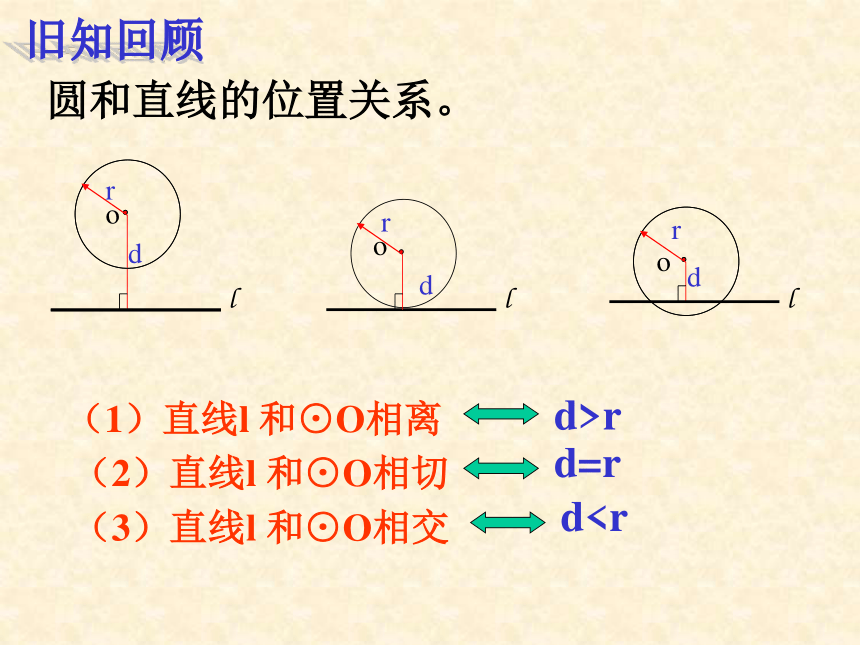
课件21张PPT。24.2.2 直线与圆的位置关系(2)(2)直线l 和⊙O相切圆和直线的位置关系。 (1)直线l 和⊙O相离(3)直线l 和⊙O相交d>rd=rd外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少?______,直线L和
⊙O有什么位置关系?
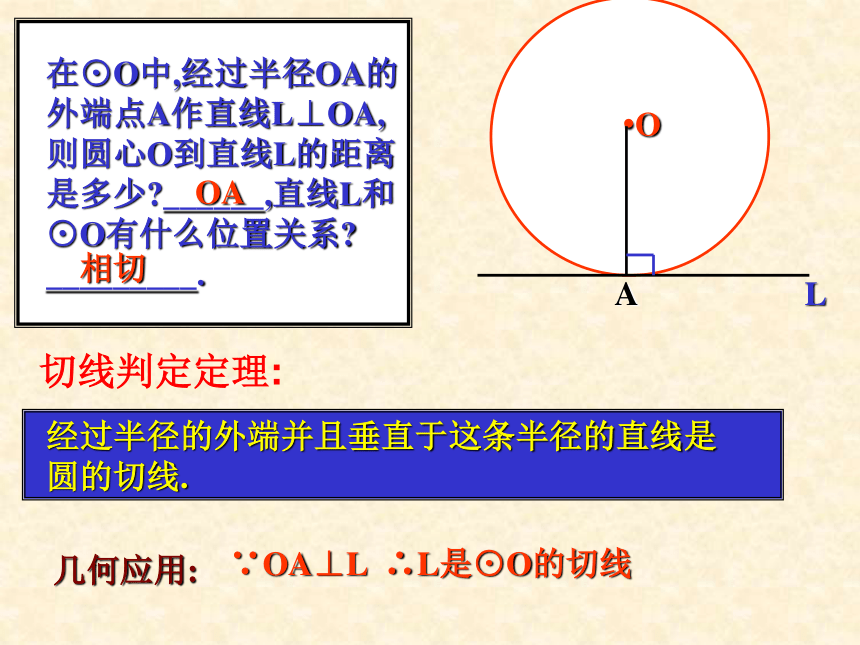
_________..OAOA相切L经过半径的外端并且垂直于这条半径的直线是
圆的切线.几何应用: ∵OA⊥L ∴L是⊙O的切线切线判定定理:1.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
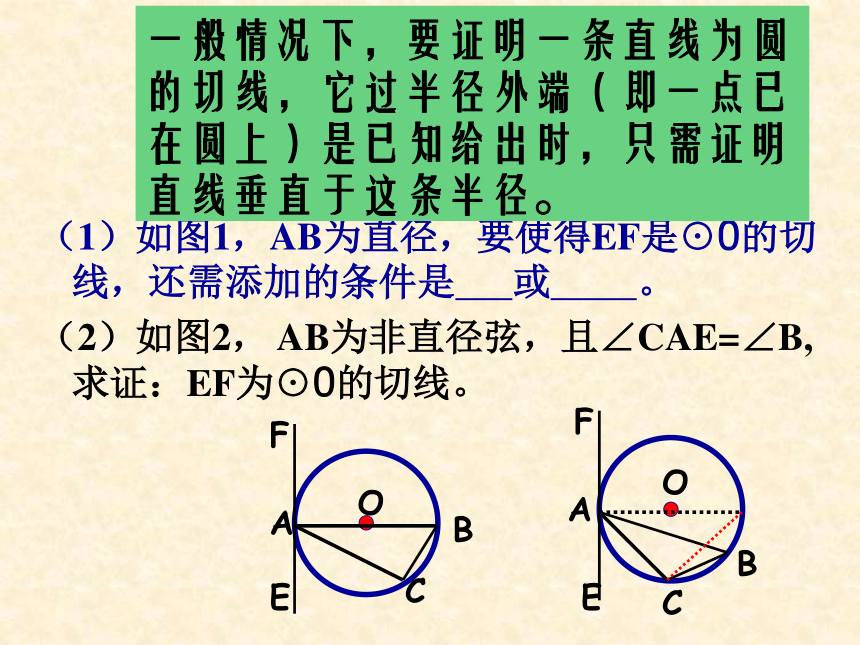
××√√√已知△ABC内接于⊙O,直线EF过点A(1)如图1,AB为直径,要使得EF是⊙O的切线,还需添加的条件是 或 。
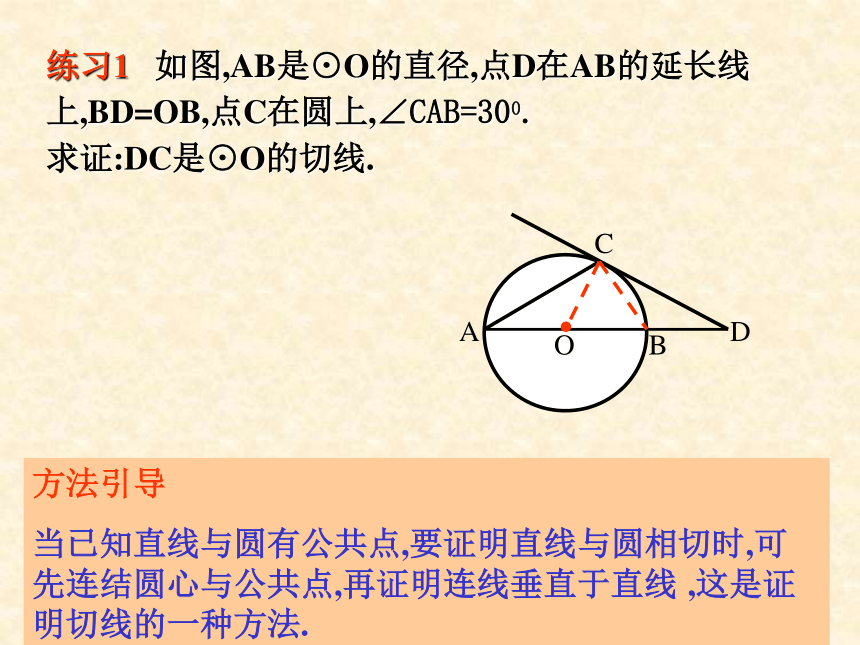
(2)如图2, AB为非直径弦,且∠CAE=∠B,求证:EF为⊙O的切线。一般情况下,要证明一条直线为圆的切线,它过半径外端(即一点已在圆上)是已知给出时,只需证明直线垂直于这条半径。练习1 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠CAB=300.
求证:DC是⊙O的切线.方法引导
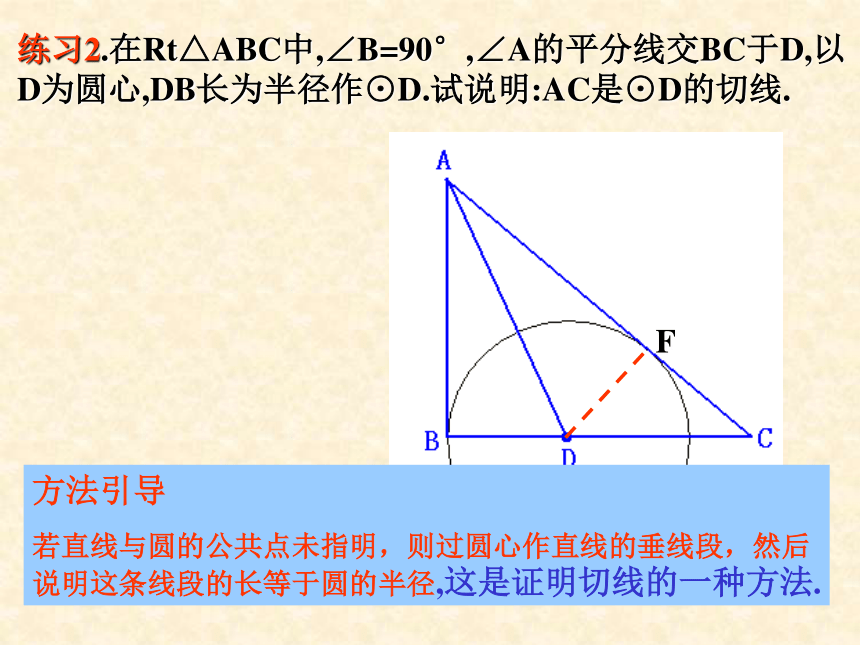
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.练习2.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F方法引导
若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径,这是证明切线的一种方法.1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
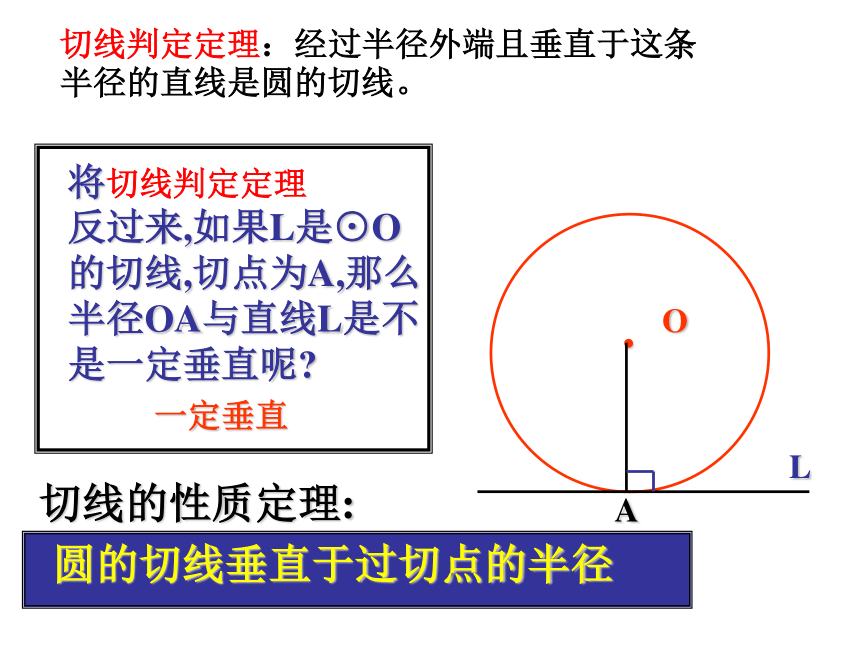
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。证明直线与圆相切有如下三种途径:即:若直线与圆的一个公共点已指明,则连接这点和圆心,说明直线垂直于经过这点的半径;若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径..OAL将切线判定定理
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径切线判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。AL1L2BO如图,AB是⊙O的直径,直线L1、L2
是⊙O的切线,A、B是切点,直线L1、L2有怎样的位置关系?
练习已知如图,半径为5cm的⊙O切AC于点B,AB=5cm,BC= cm,求∠AOC的度数.ABCOABPOC3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.www.czsx.com.cn1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。4、经过圆心垂直于切线的直线必过切点。5、经过切点垂直于切线的直线必过圆心。切线的性质:切线的性质3、4、5可归纳为:已知直线满足a、过圆心,b、过切点,c、垂直于切线中任意两个,便得到第三个结论。3.如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC,
求证:DC是⊙O的切线.如图,在梯形ABCD中,AD∥BC, ∠C=90°.且AB=AD+BC,求证:以AB为直径的⊙O与CD相切.ABCDOE1.如图所示,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:(1)AD=BD;
(2)DF是⊙O的切线.能力与拓展5.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.2.如图所示,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于F.
求证:DE是⊙O的切线如图,以Rt△ABC的直角边BC为直径
作半圆O,交斜边于D,OE∥AC交AB于E
求证:DE是⊙O的切线。选作题ADCOBE
则圆心O到直线L的距离
是多少?______,直线L和
⊙O有什么位置关系?
_________..OAOA相切L经过半径的外端并且垂直于这条半径的直线是
圆的切线.几何应用: ∵OA⊥L ∴L是⊙O的切线切线判定定理:1.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
××√√√已知△ABC内接于⊙O,直线EF过点A(1)如图1,AB为直径,要使得EF是⊙O的切线,还需添加的条件是 或 。
(2)如图2, AB为非直径弦,且∠CAE=∠B,求证:EF为⊙O的切线。一般情况下,要证明一条直线为圆的切线,它过半径外端(即一点已在圆上)是已知给出时,只需证明直线垂直于这条半径。练习1 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠CAB=300.
求证:DC是⊙O的切线.方法引导
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.练习2.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F方法引导
若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径,这是证明切线的一种方法.1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。证明直线与圆相切有如下三种途径:即:若直线与圆的一个公共点已指明,则连接这点和圆心,说明直线垂直于经过这点的半径;若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径..OAL将切线判定定理
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径切线判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。AL1L2BO如图,AB是⊙O的直径,直线L1、L2
是⊙O的切线,A、B是切点,直线L1、L2有怎样的位置关系?
练习已知如图,半径为5cm的⊙O切AC于点B,AB=5cm,BC= cm,求∠AOC的度数.ABCOABPOC3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.www.czsx.com.cn1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。4、经过圆心垂直于切线的直线必过切点。5、经过切点垂直于切线的直线必过圆心。切线的性质:切线的性质3、4、5可归纳为:已知直线满足a、过圆心,b、过切点,c、垂直于切线中任意两个,便得到第三个结论。3.如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC,
求证:DC是⊙O的切线.如图,在梯形ABCD中,AD∥BC, ∠C=90°.且AB=AD+BC,求证:以AB为直径的⊙O与CD相切.ABCDOE1.如图所示,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:(1)AD=BD;
(2)DF是⊙O的切线.能力与拓展5.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.2.如图所示,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于F.
求证:DE是⊙O的切线如图,以Rt△ABC的直角边BC为直径
作半圆O,交斜边于D,OE∥AC交AB于E
求证:DE是⊙O的切线。选作题ADCOBE
同课章节目录
