九年级数学月考复习测试卷(无答案)
图片预览


文档简介
九年级数学测试卷
一、 选择题
1. 如果,那么下列各式中不成立的是( )
. ; . ; .; ..
2. 如图,已知AB∥CD,AD与BC相交于点O,AO∶DO=1∶2,那么下列式子错误的是
(A)BO∶CO=1∶2;(B)AB∶CD=1∶2;(C)AD∶DO=3∶2;(D)CO∶BC=1∶2.
3.已知线段a、b、c,作线段x,使a:b=c:x,则正确的作法是( )
A、 ( http: / / www.21cnjy.com ) B、 ( http: / / www.21cnjy.com ) C、 ( http: / / www.21cnjy.com ) D、 ( http: / / www.21cnjy.com )
4.如果△ABC∽△DEF,且△ABC的三边长分别为3、5、6,△DEF的最短边长为9,那么△DEF的周长等于
(A)14; (B); (C)21; (D)42.
5.下列五幅图均是由边长为1的16个小正 ( http: / / www.21cnjy.com )方形组成的正方形网格,网格中的三角形的顶点都在小正方形的顶点上,那么在下列右边四幅图中的三角形,与左图中的△ABC相似的个数有
(A)1个; (B)2个; (C)3个; (D)4个.
二、填空题(本大题共12题,每题4分,满分48分)
7. 已知,线段AB=1cm,C是AB的黄金分割点,且AC>BC,则AC=
8..已知△ABC∽△DEF,其中AB=10,AC=3,BC=5,如果AB的对应边DE为2,那么△DEF的周长是 _________ ;
9..已知在△ABC中,点D、E分别在边AB、AC上,DE//BC,,那么的值等于 .
10. 两个相似三角形对应角平分线的比为2∶3,它们的面积之和
为52cm2,那么较大的三角形的面积为_____________ cm2
11. 如图,BC平分∠ABD,AB=4,BD=9,若⊿ABC∽⊿CBD,则BC= ▲ .
12. 两个相似三角形对应角平分线的比为2∶3,它们的面积之和
为52cm2,那么较大的三角形的面积为_____________ cm2
13.如图,l1∥l2∥l3,AB=AC,DE=5,那么EF= _________
.. ( http: / / www.21cnjy.com )
14、直角三角形斜边长为6,那么三角形的重心到斜边中点的距离为_______
15.如图,在平行四边形中,点是边上的黄金分割点,且,与相交于点,那么的值为 .
16. 在△ABC中,∠B=35°,AD是BC边上的高,并且AD2=BD·DC,则∠BCA的度数为 17 D、E分别是△ABC的边AB、AC的反向延长线上的点,如果,那么的值是_____ 时,DE∥BC.
18.菱形ABCD边长为4,点E在直线AD上,DE=3,联结BE与对角线AC交点M,那么的值是 .
三、解答题(本大题共7题,满分78分)
19.如图10,直线、、分别交直线于点、、,交直线于点、、
且∥∥.已知,.
(1)求的长;
(2)当,时,求的长.
20、如图,已知在平行四边形中,是上一点,与相交于点,与的延长线相交于点,已知,.
求、的长.
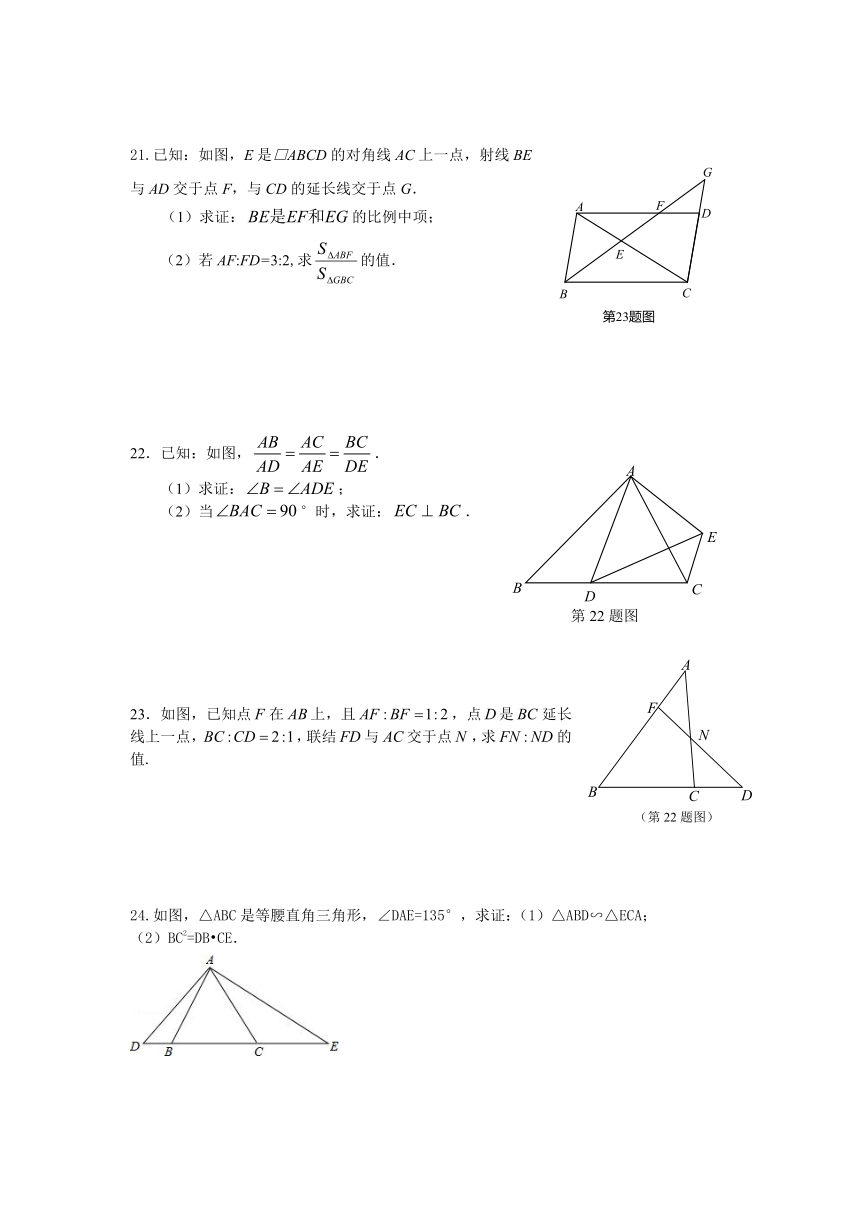
21.已知:如图,E是□ABCD的对角线AC上一点,射线BE与AD交于点F,与CD的延长线交于点G.
(1)求证:的比例中项;
(2)若AF:FD=3:2,求的值.
22.已知:如图,.
(1)求证:;
(2)当°时,求证:.
23.如图,已知点在上,且,点是延长线上一点,,联结与交于点,求的值.
24.如图,△ABC是等腰直角三角形,∠DAE=135°,求证:(1)△ABD∽△ECA;
(2)BC2=DB CE.
( http: / / www.21cnjy.com )
25.如图1,在平行四边形中,.
(1)求证:;
(2)若点、分别为边、上的两点,且.(如图2)
① 求证:∽;
② 求证:.
(图1) (图2)
26.(本题满分14分 第(1)小题4分,第(2)小题4分,第(3)小题6分)
在梯形ABCD中,AD∥BC,.(如图1)
(1)试求的度数;
(2)若E、F分别为边AD、CD上的两个动点(不与端点A、D、C重合),且始终保持,与交于点.(如图2)
①求证:∽;
②试判断的形状(从边、角两个方面考虑),并加以说明;
③设,试求关于的函数解析式,并写出定义域.
(图1)
解:(1)作,垂足为,
在四边形中,AD∥BC,,
则四边形为正方形,--------(1分)
又在中,,----(1分)
∴.-----(1分)
(2)①∵四边形为正方形,
∴,,----(1分)
又∵,
∴--------------(1分)
又∵,-------------------------------(1分)
∴∽.------------------------------------(1分)
②是等腰直角三角形,-------------------------------(1分)
∵∽,
∴,------------------------------------------(1分)
又∵,
∴∽,------------------------------------(1分)
又在中,,为等腰直角三角形,---(1分)
∴是等腰直角三角形.
③延长交的延长线于点,
易知,
∵∽,
∴,
则,
∴,
又∵,
∴,------------------------------------(1分)
∵,
∴,(0<<1). -------------(2分)
A
B
C
D
O
(第2题图)
A
C
B
A
B
C
D
E
F
图10
A
B
C
D
E
G
O
A
B
C
E
D
第22题图
(第22题图)
F
E
D
C
B
A
D
C
B
A
B
C
D
A
B
C
D
P
E
F
A
一、 选择题
1. 如果,那么下列各式中不成立的是( )
. ; . ; .; ..
2. 如图,已知AB∥CD,AD与BC相交于点O,AO∶DO=1∶2,那么下列式子错误的是
(A)BO∶CO=1∶2;(B)AB∶CD=1∶2;(C)AD∶DO=3∶2;(D)CO∶BC=1∶2.
3.已知线段a、b、c,作线段x,使a:b=c:x,则正确的作法是( )
A、 ( http: / / www.21cnjy.com ) B、 ( http: / / www.21cnjy.com ) C、 ( http: / / www.21cnjy.com ) D、 ( http: / / www.21cnjy.com )
4.如果△ABC∽△DEF,且△ABC的三边长分别为3、5、6,△DEF的最短边长为9,那么△DEF的周长等于
(A)14; (B); (C)21; (D)42.
5.下列五幅图均是由边长为1的16个小正 ( http: / / www.21cnjy.com )方形组成的正方形网格,网格中的三角形的顶点都在小正方形的顶点上,那么在下列右边四幅图中的三角形,与左图中的△ABC相似的个数有
(A)1个; (B)2个; (C)3个; (D)4个.
二、填空题(本大题共12题,每题4分,满分48分)
7. 已知,线段AB=1cm,C是AB的黄金分割点,且AC>BC,则AC=
8..已知△ABC∽△DEF,其中AB=10,AC=3,BC=5,如果AB的对应边DE为2,那么△DEF的周长是 _________ ;
9..已知在△ABC中,点D、E分别在边AB、AC上,DE//BC,,那么的值等于 .
10. 两个相似三角形对应角平分线的比为2∶3,它们的面积之和
为52cm2,那么较大的三角形的面积为_____________ cm2
11. 如图,BC平分∠ABD,AB=4,BD=9,若⊿ABC∽⊿CBD,则BC= ▲ .
12. 两个相似三角形对应角平分线的比为2∶3,它们的面积之和
为52cm2,那么较大的三角形的面积为_____________ cm2
13.如图,l1∥l2∥l3,AB=AC,DE=5,那么EF= _________
.. ( http: / / www.21cnjy.com )
14、直角三角形斜边长为6,那么三角形的重心到斜边中点的距离为_______
15.如图,在平行四边形中,点是边上的黄金分割点,且,与相交于点,那么的值为 .
16. 在△ABC中,∠B=35°,AD是BC边上的高,并且AD2=BD·DC,则∠BCA的度数为 17 D、E分别是△ABC的边AB、AC的反向延长线上的点,如果,那么的值是_____ 时,DE∥BC.
18.菱形ABCD边长为4,点E在直线AD上,DE=3,联结BE与对角线AC交点M,那么的值是 .
三、解答题(本大题共7题,满分78分)
19.如图10,直线、、分别交直线于点、、,交直线于点、、
且∥∥.已知,.
(1)求的长;
(2)当,时,求的长.
20、如图,已知在平行四边形中,是上一点,与相交于点,与的延长线相交于点,已知,.
求、的长.
21.已知:如图,E是□ABCD的对角线AC上一点,射线BE与AD交于点F,与CD的延长线交于点G.
(1)求证:的比例中项;
(2)若AF:FD=3:2,求的值.
22.已知:如图,.
(1)求证:;
(2)当°时,求证:.
23.如图,已知点在上,且,点是延长线上一点,,联结与交于点,求的值.
24.如图,△ABC是等腰直角三角形,∠DAE=135°,求证:(1)△ABD∽△ECA;
(2)BC2=DB CE.
( http: / / www.21cnjy.com )
25.如图1,在平行四边形中,.
(1)求证:;
(2)若点、分别为边、上的两点,且.(如图2)
① 求证:∽;
② 求证:.
(图1) (图2)
26.(本题满分14分 第(1)小题4分,第(2)小题4分,第(3)小题6分)
在梯形ABCD中,AD∥BC,.(如图1)
(1)试求的度数;
(2)若E、F分别为边AD、CD上的两个动点(不与端点A、D、C重合),且始终保持,与交于点.(如图2)
①求证:∽;
②试判断的形状(从边、角两个方面考虑),并加以说明;
③设,试求关于的函数解析式,并写出定义域.
(图1)
解:(1)作,垂足为,
在四边形中,AD∥BC,,
则四边形为正方形,--------(1分)
又在中,,----(1分)
∴.-----(1分)
(2)①∵四边形为正方形,
∴,,----(1分)
又∵,
∴--------------(1分)
又∵,-------------------------------(1分)
∴∽.------------------------------------(1分)
②是等腰直角三角形,-------------------------------(1分)
∵∽,
∴,------------------------------------------(1分)
又∵,
∴∽,------------------------------------(1分)
又在中,,为等腰直角三角形,---(1分)
∴是等腰直角三角形.
③延长交的延长线于点,
易知,
∵∽,
∴,
则,
∴,
又∵,
∴,------------------------------------(1分)
∵,
∴,(0<<1). -------------(2分)
A
B
C
D
O
(第2题图)
A
C
B
A
B
C
D
E
F
图10
A
B
C
D
E
G
O
A
B
C
E
D
第22题图
(第22题图)
F
E
D
C
B
A
D
C
B
A
B
C
D
A
B
C
D
P
E
F
A
同课章节目录
