山东省菏泽市曹县2022-2023学年八年级下学期期末考试数学试题(pdf版 含答案)
文档属性
| 名称 | 山东省菏泽市曹县2022-2023学年八年级下学期期末考试数学试题(pdf版 含答案) | 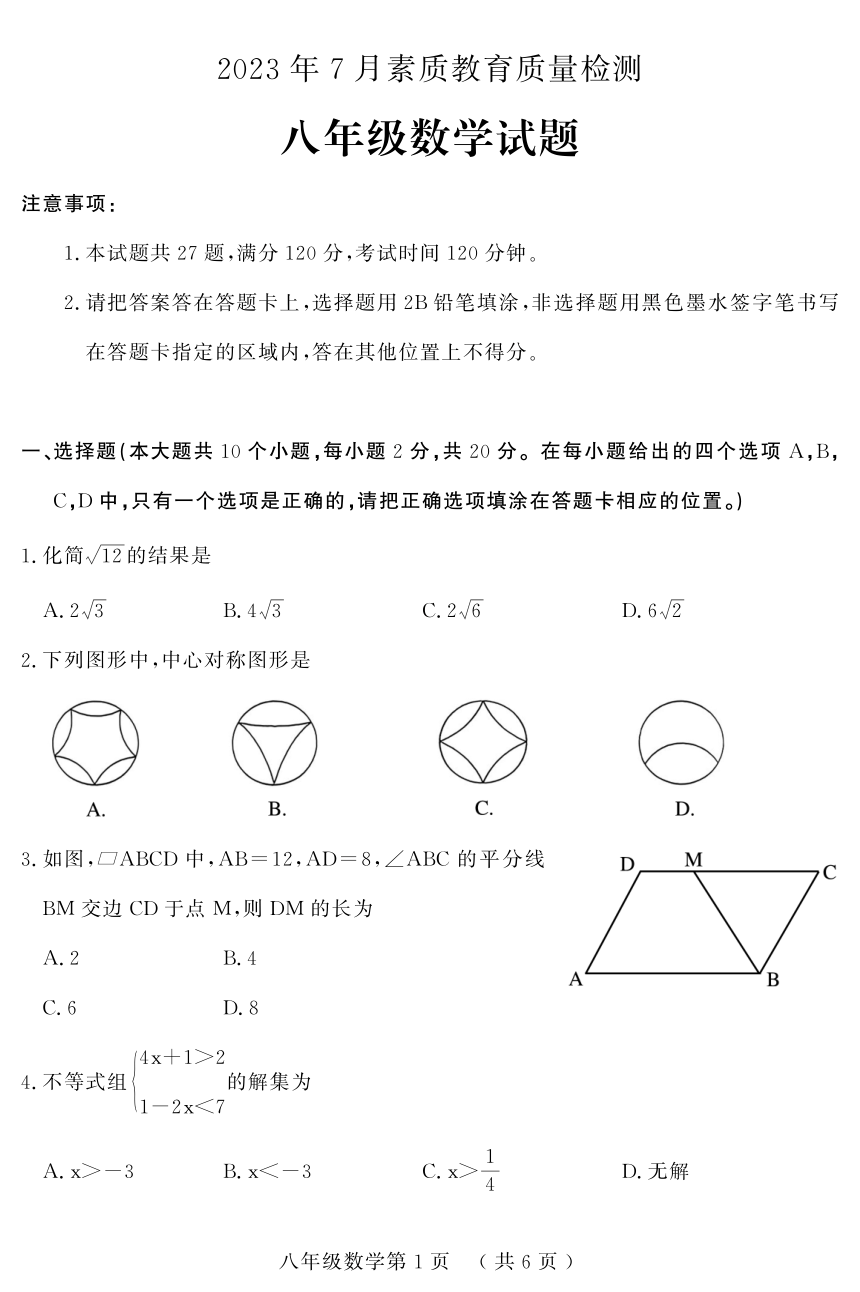 | |
| 格式 | |||
| 文件大小 | 410.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 11:16:27 | ||
图片预览



文档简介
2023年7月素质教育质量检测
八年级数学试题
注意事项:
1.本试题共27题,满分120分,考试时间120分钟。
2.请把答案答在答题卡上,选择题用2B铅笔填涂,非选择题用黑色墨水签字笔书写
在答题卡指定的区域内,答在其他位置上不得分。
一、选择题(本大题共10个小题,每小题2分,共20分。在每小题给出的四个选项A,B,
C,D中,只有一个选项是正确的,请把正确选项填涂在答题卡相应的位置。)
1.化简 12的结果是
A.23 B.43 C.26 D.62
2.下列图形中,中心对称图形是
3.如图, ABCD中,AB=12,AD=8,∠ABC的平分线
BM交边CD于点 M,则DM的长为
A.2 B.4
C.6 D.8
4x+1>2
4.不等式组 的解集为1-2x<7
1
A.x>-3 B.x<-3 C.x> 无解4 D.
八年级数学第1页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
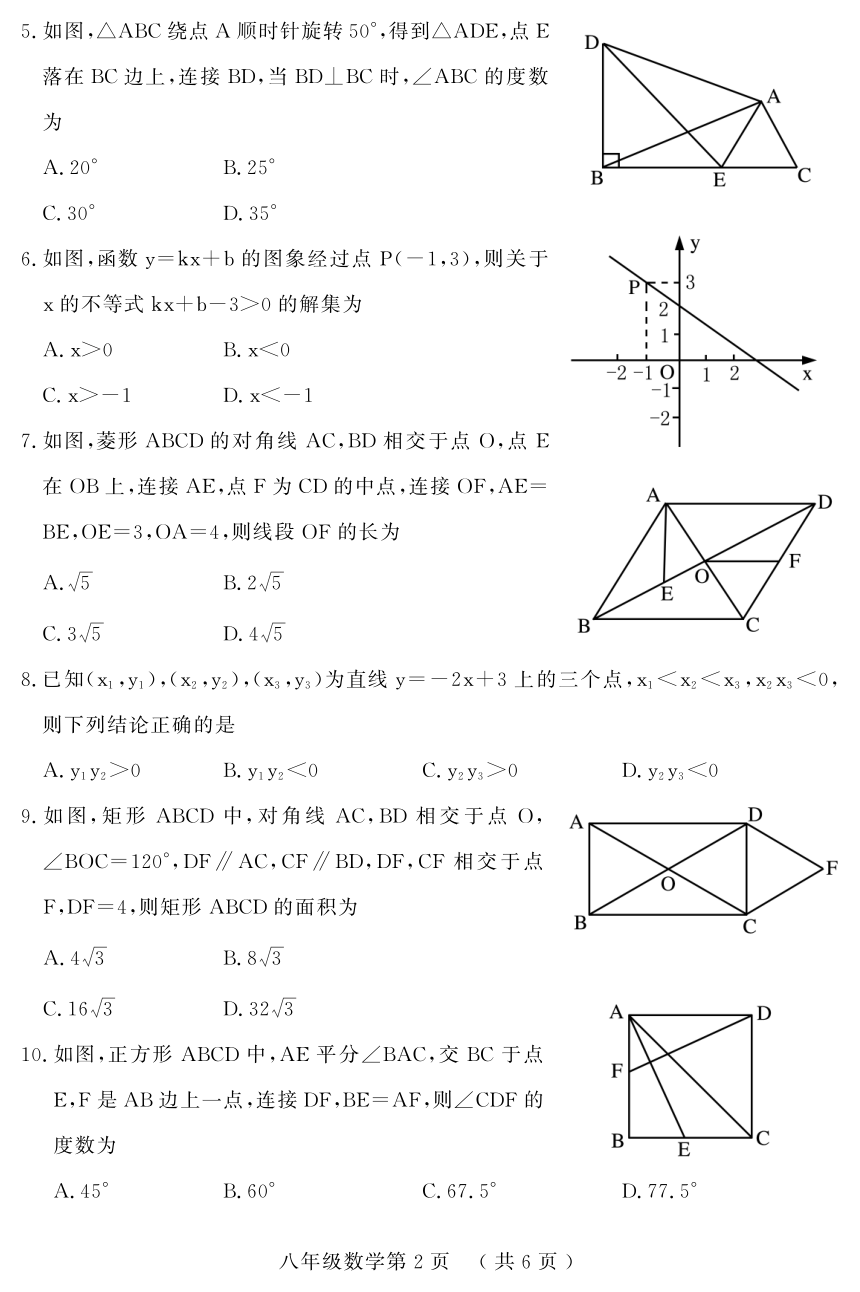
5.如图,△ABC绕点A顺时针旋转50°,得到△ADE,点E
落在BC边上,连接BD,当BD⊥BC时,∠ABC的度数
为
A.20° B.25°
C.30° D.35°
6.如图,函数y=kx+b的图象经过点P(-1,3),则关于
x的不等式kx+b-3>0的解集为
A.x>0 B.x<0
C.x>-1 D.x<-1
7.如图,菱形ABCD的对角线 AC,BD相交于点 O,点E
在OB上,连接AE,点F为CD的中点,连接OF,AE=
BE,OE=3,OA=4,则线段OF的长为
A.5 B.25
C.35 D.45
8.已知(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,x1则下列结论正确的是
A.y1y2>0 B.y1y2<0 C.y2y3>0 D.y2y3<0
9.如图,矩形 ABCD中,对角线 AC,BD相交于点 O,
∠BOC=120°,DF∥AC,CF∥BD,DF,CF相交于点
F,DF=4,则矩形ABCD的面积为
A.43 B.83
C.163 D.323
10.如图,正方形ABCD中,AE平分∠BAC,交BC于点
E,F是AB边上一点,连接DF,BE=AF,则∠CDF的
度数为
A.45° B.60° C.67.5° D.77.5°
八年级数学第2页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
二、填空题(本大题共8个小题,每小题2分,共16分,只要求把最后结果填写在答题卡的
相应区域内。)
11.若根式 1-3x在实数范围内有意义,则x的取值范围是 .
12.已知2x是216的立方根,则x+6的平方根是 .
13.不等式1-3(x-1)14.△ABC的顶点A,B的坐标分别为A(0,2),B(2,-1),平移△ABC得到△A'B'C',点
A的对应点A'的坐标为(-1,0),则点B的对应点B'的坐标为 .
15.已知x= 6- 2,则代数式2x2+42x的值为 .
2x-1<3
16.不等式组 的解集为x17.如图,菱形 ABCD的边长为4,AC是对角线,∠B=
60°,E为 AB边的中点,连接 AE,DE,则 DE的长为
.
18.如图,正方形 ABCD的边长为8,点E是 DC边的中
点,GH 垂直平分 AE,分别交BC,AE于点 G,H,则
BG的长为 .
三、解答题(本题共84分,把解答或证明过程写在答题卡的相应区域内。)
19.(每小题6分,共18分)
计算:
(1)
1 3
3 36-2 125-
(-4)2.
八年级数学第3页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
(2)(
2 1
8- )3 -
(6 2+ 24
).
(3)(6-23)2+ 27(54- 12).
20.(本题6分)
解不等式5x-3(2x-1)<2(x+6),并把解集在数轴上表示出来.
21.(本题6分)
6x+1≤4(x-1),
解不等式组: x x+5
1-4> 2 .
22.(本题8分)
1
已知 (x-2)3+32=0,3x-2y的算术平方根是6,求2 x
2-y的值.
23.(本题8分)
如图,Rt△ABC中,∠ACB=90°,D是AB边的中点,BE⊥CD,交CD的延长线于
点E,AC=4,BC=43,求△BCD的面积和BE的长.
八年级数学第4页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
24.(本题8分)
如图,菱形ABCD中,点E,F分别在边AB,AD上,AE=AF,连接CE,CF,EF,
求证:∠CEF=∠CFE.
25.(本题10分)
已知A,B两地之间有一条长440千米的高速公路,甲、乙两车分别从A,B两地
出发,沿此公路相向而行,甲车先以每小时100千米的速度匀速行驶200千米后与乙
车相遇,再以另一速度继续匀速行驶4小时到达B地,乙车匀速行驶至A地,两车到
达各自的目的地后停止,两车距A地的路程y(千米)与行驶时间x(时)的函数关系图
象如图所示.
(1)求m,n的值及乙车的速度;
(2)求两车相遇后,甲车距A地的路程y与x间的函数表达式.
八年级数学第5页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
26.(本题10分)
如图,正方形ABCD中,E是边BC的中点,将△ABE沿AE折叠,得到△AFE,
延长EF交边CD于点P.
(1)求证:DP=FP;
(2)若AB=6,求CP的长.
27.(本题10分)
某快递公司为了提高工作效率,计划购买A,B两种型号的机器人来搬运货物.已
知每台A型机器人售价1.2万元,每天搬运货物90吨,每台B型机器人售价2万元,
每天搬运货物100吨.该公司计划采购A,B两种型号的机器人共30台,必须每天搬
运货物不低于2830吨.
(1)设购买A型机器人x台,购买总金额为y万元,求y与x间的函数表达式;
(2)求购买A,B两种型号机器人分别为多少台时,购买总金额最低
八年级数学第6页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
2023年7月素质教育质量检测
八年级数学试题参考答案
一、每小题2分,共20分
1.A 2.C 3.B 4.C 5.B 6.D 7.B 8.A 9.C 10.C
二、每小题2分,共16分
1
11.x≤ (, )3 12.±3 13.x>1 14.1 -3 15.8
16.a≤2 17.27 18.1
三、本题84分
19.每小题6分,共18分
(
7
1)-12 (2)- 2- 6 (3 3
)152
20.本题6分
解:x>-3 …………………………………………………………………………… 4分
画图(略) ………………………………………………………………………… 6分
21.本题6分
6x+1≤4(x-1) ①
解: x x+5
1-4> 2 ②
5
解不等式①,得x≤- ………………………………………………………2 2
分
解不等式②,得x<-2 ………………………………………………………… 5分
5
∴不等式组的解集为x≤- ………………………………………………… 分2 6
22.本题8分
解:(x-2)3=-64
八年级数学答案第1页 (共3页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
∴x-2=-4 ∴x=-2 …………………………………………………… 4分
由3x-2y=62,得3x-2y=36
3x-36 3×(-2)-36
∴y= = =-21 ………………………………………… 7分2 2
∴ x2-y= (-2)2-(-21)= 25=5 …………………………………… 8分
23.本题8分
解:在Rt△ACB中,
AB= AC2+BC2= 42+(43)2=8 ……………………………………… 2分
∵D是AB边的中点
1 1
∴AD=BD=CD=2AB=2×8=4
1 1 1 1 1
∴S△BCD=S△ACD=2S△ACB=2×2AC
·BC= …… 分2×2×4×43=43 6
1
∵S△BCD=2CD
·BE
2S△BCD 2×43
∴BE= = =23 ……………………………………………… 8分CD 4
24.本题8分
提示:由菱形ABCD,得CB=CD,AB=AD,∠B=∠D
由AE=AF,得BE=DF,得△CBE≌△CDF ……………………………… 6分
得CE=CF,得∠CEF=∠CFE ……………………………………………… 8分
25.本题10分
:() 200 解 1m=100=2
n=m+4=2+4=6
440-200
2 =120
(千米)
∴乙车的速度为每小时120千米 ……………………………………………… 4分
八年级数学答案第2页 (共3页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
2k+b=200
(2)设y=kx+b,根据题意,得 6k+b=440
k=60
解这个方程组,得 b=80
∴甲车距A地的路程y与x间的函数表达式为y=60x+80 ……………… 10分
26.本题10分
(1)提示:连接AP,由AF=AB,AD=AB,得AD=AF
由∠AFE=∠B=90°,得∠D=∠AFP=90°,由AP=AP
得Rt△ADP≌△Rt△AFP,得DP=FP …………………………………… 5分
(2)解:设CP=x,则FP=DP=6-x,
1 1
BE=CE=EF=2BC=2×6=3
∴EP=EF+FP=3+6-x=9-x
在Rt△ECP中,(9-x)2=32+x2
∴x=4
∴CP的长为4 ……………………………………………………………… 10分
27.本题10分
解:(1)y=1.2x+2(30-x)=-0.8x+60
∴y与x间的函数表达式为y=-0.8x+60 ………………………………… 3分
(2)根据题意,得
90x+100(30-x)≥2830 ……………………………………………………… 5分
解这个不等式,得x≤17 ……………………………………………………… 7分
∵y=-0.8x+60随x的增大而减小
∴当x=17时,y有最小值
∴30-x=30-17=13(台)
∴购买A,B两种型号机器人分别为17台、13台时,购买总金额最低。 … 10分
八年级数学答案第3页 (共3页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
八年级数学试题
注意事项:
1.本试题共27题,满分120分,考试时间120分钟。
2.请把答案答在答题卡上,选择题用2B铅笔填涂,非选择题用黑色墨水签字笔书写
在答题卡指定的区域内,答在其他位置上不得分。
一、选择题(本大题共10个小题,每小题2分,共20分。在每小题给出的四个选项A,B,
C,D中,只有一个选项是正确的,请把正确选项填涂在答题卡相应的位置。)
1.化简 12的结果是
A.23 B.43 C.26 D.62
2.下列图形中,中心对称图形是
3.如图, ABCD中,AB=12,AD=8,∠ABC的平分线
BM交边CD于点 M,则DM的长为
A.2 B.4
C.6 D.8
4x+1>2
4.不等式组 的解集为1-2x<7
1
A.x>-3 B.x<-3 C.x> 无解4 D.
八年级数学第1页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
5.如图,△ABC绕点A顺时针旋转50°,得到△ADE,点E
落在BC边上,连接BD,当BD⊥BC时,∠ABC的度数
为
A.20° B.25°
C.30° D.35°
6.如图,函数y=kx+b的图象经过点P(-1,3),则关于
x的不等式kx+b-3>0的解集为
A.x>0 B.x<0
C.x>-1 D.x<-1
7.如图,菱形ABCD的对角线 AC,BD相交于点 O,点E
在OB上,连接AE,点F为CD的中点,连接OF,AE=
BE,OE=3,OA=4,则线段OF的长为
A.5 B.25
C.35 D.45
8.已知(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,x1
A.y1y2>0 B.y1y2<0 C.y2y3>0 D.y2y3<0
9.如图,矩形 ABCD中,对角线 AC,BD相交于点 O,
∠BOC=120°,DF∥AC,CF∥BD,DF,CF相交于点
F,DF=4,则矩形ABCD的面积为
A.43 B.83
C.163 D.323
10.如图,正方形ABCD中,AE平分∠BAC,交BC于点
E,F是AB边上一点,连接DF,BE=AF,则∠CDF的
度数为
A.45° B.60° C.67.5° D.77.5°
八年级数学第2页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
二、填空题(本大题共8个小题,每小题2分,共16分,只要求把最后结果填写在答题卡的
相应区域内。)
11.若根式 1-3x在实数范围内有意义,则x的取值范围是 .
12.已知2x是216的立方根,则x+6的平方根是 .
13.不等式1-3(x-1)
A的对应点A'的坐标为(-1,0),则点B的对应点B'的坐标为 .
15.已知x= 6- 2,则代数式2x2+42x的值为 .
2x-1<3
16.不等式组 的解集为x
60°,E为 AB边的中点,连接 AE,DE,则 DE的长为
.
18.如图,正方形 ABCD的边长为8,点E是 DC边的中
点,GH 垂直平分 AE,分别交BC,AE于点 G,H,则
BG的长为 .
三、解答题(本题共84分,把解答或证明过程写在答题卡的相应区域内。)
19.(每小题6分,共18分)
计算:
(1)
1 3
3 36-2 125-
(-4)2.
八年级数学第3页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
(2)(
2 1
8- )3 -
(6 2+ 24
).
(3)(6-23)2+ 27(54- 12).
20.(本题6分)
解不等式5x-3(2x-1)<2(x+6),并把解集在数轴上表示出来.
21.(本题6分)
6x+1≤4(x-1),
解不等式组: x x+5
1-4> 2 .
22.(本题8分)
1
已知 (x-2)3+32=0,3x-2y的算术平方根是6,求2 x
2-y的值.
23.(本题8分)
如图,Rt△ABC中,∠ACB=90°,D是AB边的中点,BE⊥CD,交CD的延长线于
点E,AC=4,BC=43,求△BCD的面积和BE的长.
八年级数学第4页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
24.(本题8分)
如图,菱形ABCD中,点E,F分别在边AB,AD上,AE=AF,连接CE,CF,EF,
求证:∠CEF=∠CFE.
25.(本题10分)
已知A,B两地之间有一条长440千米的高速公路,甲、乙两车分别从A,B两地
出发,沿此公路相向而行,甲车先以每小时100千米的速度匀速行驶200千米后与乙
车相遇,再以另一速度继续匀速行驶4小时到达B地,乙车匀速行驶至A地,两车到
达各自的目的地后停止,两车距A地的路程y(千米)与行驶时间x(时)的函数关系图
象如图所示.
(1)求m,n的值及乙车的速度;
(2)求两车相遇后,甲车距A地的路程y与x间的函数表达式.
八年级数学第5页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
26.(本题10分)
如图,正方形ABCD中,E是边BC的中点,将△ABE沿AE折叠,得到△AFE,
延长EF交边CD于点P.
(1)求证:DP=FP;
(2)若AB=6,求CP的长.
27.(本题10分)
某快递公司为了提高工作效率,计划购买A,B两种型号的机器人来搬运货物.已
知每台A型机器人售价1.2万元,每天搬运货物90吨,每台B型机器人售价2万元,
每天搬运货物100吨.该公司计划采购A,B两种型号的机器人共30台,必须每天搬
运货物不低于2830吨.
(1)设购买A型机器人x台,购买总金额为y万元,求y与x间的函数表达式;
(2)求购买A,B两种型号机器人分别为多少台时,购买总金额最低
八年级数学第6页 (共6页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
2023年7月素质教育质量检测
八年级数学试题参考答案
一、每小题2分,共20分
1.A 2.C 3.B 4.C 5.B 6.D 7.B 8.A 9.C 10.C
二、每小题2分,共16分
1
11.x≤ (, )3 12.±3 13.x>1 14.1 -3 15.8
16.a≤2 17.27 18.1
三、本题84分
19.每小题6分,共18分
(
7
1)-12 (2)- 2- 6 (3 3
)152
20.本题6分
解:x>-3 …………………………………………………………………………… 4分
画图(略) ………………………………………………………………………… 6分
21.本题6分
6x+1≤4(x-1) ①
解: x x+5
1-4> 2 ②
5
解不等式①,得x≤- ………………………………………………………2 2
分
解不等式②,得x<-2 ………………………………………………………… 5分
5
∴不等式组的解集为x≤- ………………………………………………… 分2 6
22.本题8分
解:(x-2)3=-64
八年级数学答案第1页 (共3页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
∴x-2=-4 ∴x=-2 …………………………………………………… 4分
由3x-2y=62,得3x-2y=36
3x-36 3×(-2)-36
∴y= = =-21 ………………………………………… 7分2 2
∴ x2-y= (-2)2-(-21)= 25=5 …………………………………… 8分
23.本题8分
解:在Rt△ACB中,
AB= AC2+BC2= 42+(43)2=8 ……………………………………… 2分
∵D是AB边的中点
1 1
∴AD=BD=CD=2AB=2×8=4
1 1 1 1 1
∴S△BCD=S△ACD=2S△ACB=2×2AC
·BC= …… 分2×2×4×43=43 6
1
∵S△BCD=2CD
·BE
2S△BCD 2×43
∴BE= = =23 ……………………………………………… 8分CD 4
24.本题8分
提示:由菱形ABCD,得CB=CD,AB=AD,∠B=∠D
由AE=AF,得BE=DF,得△CBE≌△CDF ……………………………… 6分
得CE=CF,得∠CEF=∠CFE ……………………………………………… 8分
25.本题10分
:() 200 解 1m=100=2
n=m+4=2+4=6
440-200
2 =120
(千米)
∴乙车的速度为每小时120千米 ……………………………………………… 4分
八年级数学答案第2页 (共3页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
2k+b=200
(2)设y=kx+b,根据题意,得 6k+b=440
k=60
解这个方程组,得 b=80
∴甲车距A地的路程y与x间的函数表达式为y=60x+80 ……………… 10分
26.本题10分
(1)提示:连接AP,由AF=AB,AD=AB,得AD=AF
由∠AFE=∠B=90°,得∠D=∠AFP=90°,由AP=AP
得Rt△ADP≌△Rt△AFP,得DP=FP …………………………………… 5分
(2)解:设CP=x,则FP=DP=6-x,
1 1
BE=CE=EF=2BC=2×6=3
∴EP=EF+FP=3+6-x=9-x
在Rt△ECP中,(9-x)2=32+x2
∴x=4
∴CP的长为4 ……………………………………………………………… 10分
27.本题10分
解:(1)y=1.2x+2(30-x)=-0.8x+60
∴y与x间的函数表达式为y=-0.8x+60 ………………………………… 3分
(2)根据题意,得
90x+100(30-x)≥2830 ……………………………………………………… 5分
解这个不等式,得x≤17 ……………………………………………………… 7分
∵y=-0.8x+60随x的增大而减小
∴当x=17时,y有最小值
∴30-x=30-17=13(台)
∴购买A,B两种型号机器人分别为17台、13台时,购买总金额最低。 … 10分
八年级数学答案第3页 (共3页 )
{#{QQABAQaUggCgABJAARgCEQEiCEIQkBECAAgOQFAIIAAACBNABAA=}#}
同课章节目录
