14.2_乘法公式_同步测控优化训练(含答案)
文档属性
| 名称 | 14.2_乘法公式_同步测控优化训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 89.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-24 12:33:32 | ||
图片预览




文档简介
14.2 乘法公式
一、课前预习 (5分钟训练)
1.下列各式运算正确的是( )
A.a2+a3=a5 B.a2·a3=a5 C.(ab2)3=ab6 D.a10÷a2=a5
2. 用乘法公式计算:
(1)5012; (2)99.82;
(3)60×59; (4)2 0052-2 004×2 006.
二、课中强化(10分钟训练)
1.计算:
(1)(a2+1)(a2-1)-(-a2)·a2; (2)(2a-b)(2a+b)-(-3a-b)(-3a+b);
(3)x2-(4-x)2; (4)(3x-2y)2-4(2x-y)(x-y).
2.已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
3.已知△ABC的三边a、b、c满足a2+b2+c2-ab-bc-ac=0,试判断△ABC的形状.
4.解方程:
(1)9x(4x-7)-(6x+5)(6x-5)+38=0;(2)(y2-3y+2)(y2+3y-2)=y2(y+3)(y-3).
三、课后巩固(30分钟训练)
1.下列各式中,相等关系一定成立的是( )
A.(x-y)2=(y-x)2 B.(x+6)(x-6)=x2-6
C.(x+y)2=x2+y2 D.x2+2xy2-y2=(x+y)2
2.下列运算正确的是( )
A.(a+3)2=a2+9 B.(x-y)2=x2-xy+y2
C.(1-m)2=1-2m+m2 D.(x2-y2)(x+y)(x-y)=x4-y4
3.将面积为a2的正方形边长增加2,则正方形的面积增加了( )
A.4 B.2a+4 C.4a+4 D.4a
4.下列多项式乘法中,不能用平方差公式计算的是( )
A.(a+1)(2a-2) B.(2x-3)(-2x+3)
C.(2y-)(+2y) D.(3m-2n)(-3m-2n)
5.不等式(2x-1)2-(1-3x)2<5(1-x)(x+1)的解集是( )
A.x>-2.5 B.x<-2.5 C.x>2.5 D.x<2.5
6.计算:
(1)(1.2x-y)(-y-1.2x); (2)15×(-14);
(3)[2x2-(x+y)(x-y)][(z-x)(x+z)+(y-z)(y+z)];
(4)(a-2b+3c)(a+2b-3c).
7.(1)已知x+y=6,xy=4,求①x2+y2,②(x-y)2,③x2+xy+y2的值.
(2)已知a(a-3)-(a2-3b)=9,求-ab的值.
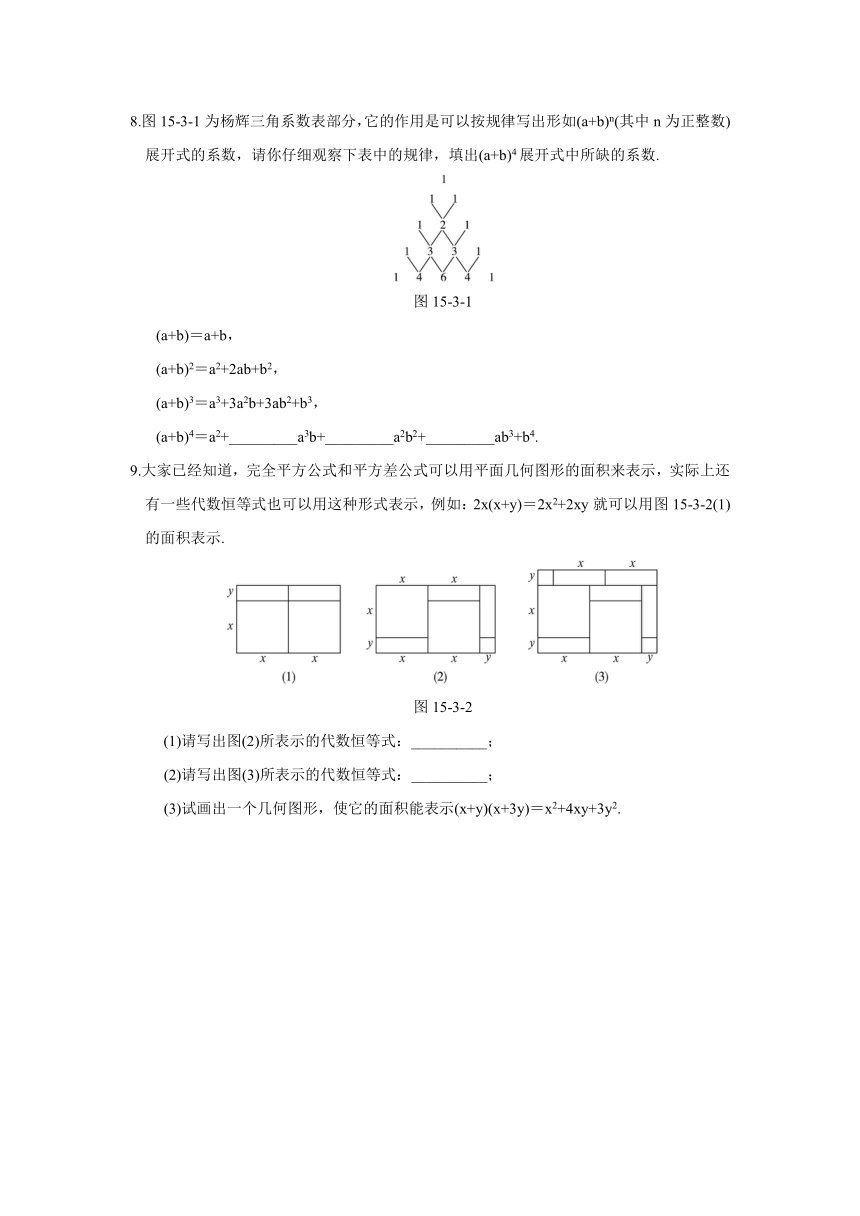
8.图15-3-1为杨辉三角系数表部分, ( http: / / www.21cnjy.com )它的作用是可以按规律写出形如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的系数.
( http: / / www.21cnjy.com )
图15-3-1
(a+b)=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
(a+b)4=a2+_________a3b+_________a2b2+_________ab3+b4.
9.大家已经知道,完全平方公式和平方差公式 ( http: / / www.21cnjy.com )可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x2+2xy就可以用图15-3-2(1)的面积表示.
( http: / / www.21cnjy.com )
图15-3-2
(1)请写出图(2)所表示的代数恒等式:__________;
(2)请写出图(3)所表示的代数恒等式:__________;
(3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2.
10.如图15-3-3所示,长方形ABCD ( http: / / www.21cnjy.com )被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求长方形ABCD中最大正方形与最小正方形的面积之差.
( http: / / www.21cnjy.com )
图15-3-3
参考答案
一、课前预习 (5分钟训练)
1.下列各式运算正确的是( )
A.a2+a3=a5 B.a2·a3=a5 C.(ab2)3=ab6 D.a10÷a2=a5
思路解析:考查整式的运算法则,A中两式不为同类项,不能合并,C中a的指数应为3,D中除法时指数应为分子的指数减分母的指数,即结果应为a8.
答案:B
2.计算:
(1)5012; (2)99.82;
(3)60×59; (4)2 0052-2 004×2 006.
思路分析:本题是利用平方差公式和完全平方公式进行简便运算,关键是写成公式的形式.
解:(1)5012=(500+1)2=5002+2×500×1+12=250 000+1 000+1=251 001.
(2)99.82=(100-0.2)2=1002-2×100×0.2+0.22=10 000-40+0.04=9 960.04.
(3)60×59=(60+)(60-)=602-()2=3 600-=3 599.
(4)原式=2 0052-(2 005-1)×(2 005+1)=2 0052-(2 0052-1)=1.
二、课中强化(10分钟训练)
1.计算:
(1)(a2+1)(a2-1)-(-a2)·a2; (2)(2a-b)(2a+b)-(-3a-b)(-3a+b);
(3)x2-(4-x)2; (4)(3x-2y)2-4(2x-y)(x-y).
思路分析:观察每个题的特征,符合完全平方公式的特征,就利用完全平方公式,符合平方差公式的特征,就利用平方差公式,结果注意合并同类项.
解:(1)原式=a4-1+a4=2a4-1.
(2)原式=4a2-b2-(9a2-b2)=4a2-b2-9a2+b2=-5a2.
(3)原式=x2-(16-8x+x2)=x2-16+8x-x2=8x-16.
(4)原式=9x2-12xy+4y2-4(2x2-3xy+y2)=9x2-12xy+4y2-8x2+12xy-4y2=x2.
2.已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
思路分析:由于(a+b)2 ( http: / / www.21cnjy.com )和(a-b)2的展开式中都只含有a2+b2和ab,所以把(a+b)2和(a-b)2展开,已知的两个等式可看成是关于a2+b2和ab的二元一次方程组,可求a2+b2和ab的值.
解:由(a+b)2=7,得a2+2ab ( http: / / www.21cnjy.com )+b2=7. ①
由(a-b)2=4,得a2-2ab ( http: / / www.21cnjy.com )+b2=4. ②
①+②得2(a2+b2)=11,∴a2+b2=.
①-②得4ab=3,∴ab=.
3.已知△ABC的三边a、b、c满足a2+b2+c2-ab-bc-ac=0,试判断△ABC的形状.
思路分析:式子a2+b2+c2-a ( http: / / www.21cnjy.com )b-bc-ac=0体现了三角形三边关系,从形式上看与完全平方式相仿,但差着2ab中的2倍,因此可以对等式两边都扩大2倍,从而得到结论.
解:∵a2+b2+c2-ab-bc-ac=0,
∴2a2+2b2+2c2-2ab-2bc-2ac=0,
即(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)=0.
∴a-b=0,b-c=0,c-a=0,即a=b=c.
∴△ABC是等边三角形.
4.解方程:
(1)9x(4x-7)-(6x+5)(6x-5)+38=0;(2)(y2-3y+2)(y2+3y-2)=y2(y+3)(y-3).
思路分析:按运算要求化简方程.
解:(1)36x2-63x-[(6x)2-25]+38=0,
63x=63,
x=1.
(2)[y2-(3y-2)][y2+(3y-2)]=y2(y2-9),
y4-(3y-2)2=y4-9y2,
y4-9y2+12y-4=y4-9y2,
12y=4,
y=.
三、课后巩固(30分钟训练)
1.下列各式中,相等关系一定成立的是( )
A.(x-y)2=(y-x)2 B.(x+6)(x-6)=x2-6
C.(x+y)2=x2+y2 D.x2+2xy2-y2=(x+y)2
思路解析:互为相反数的偶次幂相等.用两个乘法公式计算时,分清其特点.
答案:A
2.下列运算正确的是( )
A.(a+3)2=a2+9 B.(x-y)2=x2-xy+y2
C.(1-m)2=1-2m+m2 D.(x2-y2)(x+y)(x-y)=x4-y4
答案:C
3.将面积为a2的正方形边长增加2,则正方形的面积增加了( )
A.4 B.2a+4 C.4a+4 D.4a
思路解析:用面积公式列出算式(a+2)2-a2,用平方差公式计算.
答案:C
4.下列多项式乘法中,不能用平方差公式计算的是( )
A.(a+1)(2a-2) B.(2x-3)(-2x+3)
C.(2y-)(+2y) D.(3m-2n)(-3m-2n)
思路解析:平方差公式的特点为两个数的和乘以两个数的差.
答案:B
5.不等式(2x-1)2-(1-3x)2<5(1-x)(x+1)的解集是( )
A.x>-2.5 B.x<-2.5 C.x>2.5 D.x<2.5
思路解析:用平方差公式化简,移项合并同类项.
答案:D
6.计算:
(1)(1.2x-y)(-y-1.2x); (2)15×(-14);
(3)[2x2-(x+y)(x-y)][(z-x)(x+z)+(y-z)(y+z)];
(4)(a-2b+3c)(a+2b-3c).
解:(1)用平方差公式来做,但要注意-y和-y是相同项,1.2x和-1.2x是相反项.原式=y2-1.44x2.
(2)原式=-(15+)(15-)=-(152-)=-224.
(3)原式=[2x2-(x2-y2)](z2-x2+y2-z2)=(x2+y2)(-x2+y2)=y4-x4.
(4)原式=[a-(2b-3c)][a+(2 ( http: / / www.21cnjy.com )b-3c)]=a2-(2b-3c)2=a2-(4b2-12bc+9c2)=a2-4b2+12bc-9c2.
7.(1)已知x+y=6,xy=4,求①x2+y2,②(x-y)2,③x2+xy+y2的值.
(2)已知a(a-3)-(a2-3b)=9,求-ab的值.
思路分析:知道整式的变形(x+y)2-(x-y)2=4xy等.
解:(1)①x2+y2=(x+y)2-2xy=62-2×4=36-8=28.
②(x-y)2=(x+y)2-4xy=62-4×4=36-16=20.
③x2+xy+y2=28+4=32.
(2)由a(a-3)-(a2-3b)=9,得到-3a+3b=9,∴b-a=3.
.
8.图15-3-1为杨辉三 ( http: / / www.21cnjy.com )角系数表部分,它的作用是可以按规律写出形如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的系数.
( http: / / www.21cnjy.com )
图15-3-1
(a+b)=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
(a+b)4=a2+_________a3b+_________a2b2+_________ab3+b4.
思路解析:弄清杨辉三角系 ( http: / / www.21cnjy.com )数中的每一层均是a+b的几次方的系数.第一层为(a+b)0的系数;第二层为(a+b)1的各项系数,依次类推,第五层是(a+b)4的各项系数.
答案:4 6 4
9.大家已经知道,完全平方公式和平方差 ( http: / / www.21cnjy.com )公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x2+2xy就可以用图15-3-2(1)的面积表示.
( http: / / www.21cnjy.com )
图15-3-2
(1)请写出图(2)所表示的代数恒等式:__________;
(2)请写出图(3)所表示的代数恒等式:__________;
(3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2.
思路分析:这实际上是一种图形的两种面积表示方法,所以它们是相等的.计算面积时,列出的是整式的乘法.
解:(1)(x+y)(2x+y)=2x2+3xy+y2
(2)(2x+y)(x+2y)=2x2+5xy+2y2
(3)答案不唯一,如图:
( http: / / www.21cnjy.com )
10.如图15-3-3所示,长方形AB ( http: / / www.21cnjy.com )CD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求长方形ABCD中最大正方形与最小正方形的面积之差.
( http: / / www.21cnjy.com )
图15-3-3
思路分析:因为小正方形的面积为4, ( http: / / www.21cnjy.com )所以它的边长为2.显然它是最小的正方形.其余正方形的边长是b=a+2,c=b+2=a+4,d=c+2=a+6,可见边长为d的正方形是最大的,因此可求得两正方形面积差.
解:由题意,得b=a+2,c=b+2=a+4,d=c+2=a+6,
∵AB=DC,∴d+c=b+2a.
∴a+6+a+4=a+2+2a.∴a=8.
∴两正方形的面积差为d2-4=(a+6)2-4=(8+6)2-4=192.
一、课前预习 (5分钟训练)
1.下列各式运算正确的是( )
A.a2+a3=a5 B.a2·a3=a5 C.(ab2)3=ab6 D.a10÷a2=a5
2. 用乘法公式计算:
(1)5012; (2)99.82;
(3)60×59; (4)2 0052-2 004×2 006.
二、课中强化(10分钟训练)
1.计算:
(1)(a2+1)(a2-1)-(-a2)·a2; (2)(2a-b)(2a+b)-(-3a-b)(-3a+b);
(3)x2-(4-x)2; (4)(3x-2y)2-4(2x-y)(x-y).
2.已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
3.已知△ABC的三边a、b、c满足a2+b2+c2-ab-bc-ac=0,试判断△ABC的形状.
4.解方程:
(1)9x(4x-7)-(6x+5)(6x-5)+38=0;(2)(y2-3y+2)(y2+3y-2)=y2(y+3)(y-3).
三、课后巩固(30分钟训练)
1.下列各式中,相等关系一定成立的是( )
A.(x-y)2=(y-x)2 B.(x+6)(x-6)=x2-6
C.(x+y)2=x2+y2 D.x2+2xy2-y2=(x+y)2
2.下列运算正确的是( )
A.(a+3)2=a2+9 B.(x-y)2=x2-xy+y2
C.(1-m)2=1-2m+m2 D.(x2-y2)(x+y)(x-y)=x4-y4
3.将面积为a2的正方形边长增加2,则正方形的面积增加了( )
A.4 B.2a+4 C.4a+4 D.4a
4.下列多项式乘法中,不能用平方差公式计算的是( )
A.(a+1)(2a-2) B.(2x-3)(-2x+3)
C.(2y-)(+2y) D.(3m-2n)(-3m-2n)
5.不等式(2x-1)2-(1-3x)2<5(1-x)(x+1)的解集是( )
A.x>-2.5 B.x<-2.5 C.x>2.5 D.x<2.5
6.计算:
(1)(1.2x-y)(-y-1.2x); (2)15×(-14);
(3)[2x2-(x+y)(x-y)][(z-x)(x+z)+(y-z)(y+z)];
(4)(a-2b+3c)(a+2b-3c).
7.(1)已知x+y=6,xy=4,求①x2+y2,②(x-y)2,③x2+xy+y2的值.
(2)已知a(a-3)-(a2-3b)=9,求-ab的值.
8.图15-3-1为杨辉三角系数表部分, ( http: / / www.21cnjy.com )它的作用是可以按规律写出形如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的系数.
( http: / / www.21cnjy.com )
图15-3-1
(a+b)=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
(a+b)4=a2+_________a3b+_________a2b2+_________ab3+b4.
9.大家已经知道,完全平方公式和平方差公式 ( http: / / www.21cnjy.com )可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x2+2xy就可以用图15-3-2(1)的面积表示.
( http: / / www.21cnjy.com )
图15-3-2
(1)请写出图(2)所表示的代数恒等式:__________;
(2)请写出图(3)所表示的代数恒等式:__________;
(3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2.
10.如图15-3-3所示,长方形ABCD ( http: / / www.21cnjy.com )被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求长方形ABCD中最大正方形与最小正方形的面积之差.
( http: / / www.21cnjy.com )
图15-3-3
参考答案
一、课前预习 (5分钟训练)
1.下列各式运算正确的是( )
A.a2+a3=a5 B.a2·a3=a5 C.(ab2)3=ab6 D.a10÷a2=a5
思路解析:考查整式的运算法则,A中两式不为同类项,不能合并,C中a的指数应为3,D中除法时指数应为分子的指数减分母的指数,即结果应为a8.
答案:B
2.计算:
(1)5012; (2)99.82;
(3)60×59; (4)2 0052-2 004×2 006.
思路分析:本题是利用平方差公式和完全平方公式进行简便运算,关键是写成公式的形式.
解:(1)5012=(500+1)2=5002+2×500×1+12=250 000+1 000+1=251 001.
(2)99.82=(100-0.2)2=1002-2×100×0.2+0.22=10 000-40+0.04=9 960.04.
(3)60×59=(60+)(60-)=602-()2=3 600-=3 599.
(4)原式=2 0052-(2 005-1)×(2 005+1)=2 0052-(2 0052-1)=1.
二、课中强化(10分钟训练)
1.计算:
(1)(a2+1)(a2-1)-(-a2)·a2; (2)(2a-b)(2a+b)-(-3a-b)(-3a+b);
(3)x2-(4-x)2; (4)(3x-2y)2-4(2x-y)(x-y).
思路分析:观察每个题的特征,符合完全平方公式的特征,就利用完全平方公式,符合平方差公式的特征,就利用平方差公式,结果注意合并同类项.
解:(1)原式=a4-1+a4=2a4-1.
(2)原式=4a2-b2-(9a2-b2)=4a2-b2-9a2+b2=-5a2.
(3)原式=x2-(16-8x+x2)=x2-16+8x-x2=8x-16.
(4)原式=9x2-12xy+4y2-4(2x2-3xy+y2)=9x2-12xy+4y2-8x2+12xy-4y2=x2.
2.已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
思路分析:由于(a+b)2 ( http: / / www.21cnjy.com )和(a-b)2的展开式中都只含有a2+b2和ab,所以把(a+b)2和(a-b)2展开,已知的两个等式可看成是关于a2+b2和ab的二元一次方程组,可求a2+b2和ab的值.
解:由(a+b)2=7,得a2+2ab ( http: / / www.21cnjy.com )+b2=7. ①
由(a-b)2=4,得a2-2ab ( http: / / www.21cnjy.com )+b2=4. ②
①+②得2(a2+b2)=11,∴a2+b2=.
①-②得4ab=3,∴ab=.
3.已知△ABC的三边a、b、c满足a2+b2+c2-ab-bc-ac=0,试判断△ABC的形状.
思路分析:式子a2+b2+c2-a ( http: / / www.21cnjy.com )b-bc-ac=0体现了三角形三边关系,从形式上看与完全平方式相仿,但差着2ab中的2倍,因此可以对等式两边都扩大2倍,从而得到结论.
解:∵a2+b2+c2-ab-bc-ac=0,
∴2a2+2b2+2c2-2ab-2bc-2ac=0,
即(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)=0.
∴a-b=0,b-c=0,c-a=0,即a=b=c.
∴△ABC是等边三角形.
4.解方程:
(1)9x(4x-7)-(6x+5)(6x-5)+38=0;(2)(y2-3y+2)(y2+3y-2)=y2(y+3)(y-3).
思路分析:按运算要求化简方程.
解:(1)36x2-63x-[(6x)2-25]+38=0,
63x=63,
x=1.
(2)[y2-(3y-2)][y2+(3y-2)]=y2(y2-9),
y4-(3y-2)2=y4-9y2,
y4-9y2+12y-4=y4-9y2,
12y=4,
y=.
三、课后巩固(30分钟训练)
1.下列各式中,相等关系一定成立的是( )
A.(x-y)2=(y-x)2 B.(x+6)(x-6)=x2-6
C.(x+y)2=x2+y2 D.x2+2xy2-y2=(x+y)2
思路解析:互为相反数的偶次幂相等.用两个乘法公式计算时,分清其特点.
答案:A
2.下列运算正确的是( )
A.(a+3)2=a2+9 B.(x-y)2=x2-xy+y2
C.(1-m)2=1-2m+m2 D.(x2-y2)(x+y)(x-y)=x4-y4
答案:C
3.将面积为a2的正方形边长增加2,则正方形的面积增加了( )
A.4 B.2a+4 C.4a+4 D.4a
思路解析:用面积公式列出算式(a+2)2-a2,用平方差公式计算.
答案:C
4.下列多项式乘法中,不能用平方差公式计算的是( )
A.(a+1)(2a-2) B.(2x-3)(-2x+3)
C.(2y-)(+2y) D.(3m-2n)(-3m-2n)
思路解析:平方差公式的特点为两个数的和乘以两个数的差.
答案:B
5.不等式(2x-1)2-(1-3x)2<5(1-x)(x+1)的解集是( )
A.x>-2.5 B.x<-2.5 C.x>2.5 D.x<2.5
思路解析:用平方差公式化简,移项合并同类项.
答案:D
6.计算:
(1)(1.2x-y)(-y-1.2x); (2)15×(-14);
(3)[2x2-(x+y)(x-y)][(z-x)(x+z)+(y-z)(y+z)];
(4)(a-2b+3c)(a+2b-3c).
解:(1)用平方差公式来做,但要注意-y和-y是相同项,1.2x和-1.2x是相反项.原式=y2-1.44x2.
(2)原式=-(15+)(15-)=-(152-)=-224.
(3)原式=[2x2-(x2-y2)](z2-x2+y2-z2)=(x2+y2)(-x2+y2)=y4-x4.
(4)原式=[a-(2b-3c)][a+(2 ( http: / / www.21cnjy.com )b-3c)]=a2-(2b-3c)2=a2-(4b2-12bc+9c2)=a2-4b2+12bc-9c2.
7.(1)已知x+y=6,xy=4,求①x2+y2,②(x-y)2,③x2+xy+y2的值.
(2)已知a(a-3)-(a2-3b)=9,求-ab的值.
思路分析:知道整式的变形(x+y)2-(x-y)2=4xy等.
解:(1)①x2+y2=(x+y)2-2xy=62-2×4=36-8=28.
②(x-y)2=(x+y)2-4xy=62-4×4=36-16=20.
③x2+xy+y2=28+4=32.
(2)由a(a-3)-(a2-3b)=9,得到-3a+3b=9,∴b-a=3.
.
8.图15-3-1为杨辉三 ( http: / / www.21cnjy.com )角系数表部分,它的作用是可以按规律写出形如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的系数.
( http: / / www.21cnjy.com )
图15-3-1
(a+b)=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
(a+b)4=a2+_________a3b+_________a2b2+_________ab3+b4.
思路解析:弄清杨辉三角系 ( http: / / www.21cnjy.com )数中的每一层均是a+b的几次方的系数.第一层为(a+b)0的系数;第二层为(a+b)1的各项系数,依次类推,第五层是(a+b)4的各项系数.
答案:4 6 4
9.大家已经知道,完全平方公式和平方差 ( http: / / www.21cnjy.com )公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x2+2xy就可以用图15-3-2(1)的面积表示.
( http: / / www.21cnjy.com )
图15-3-2
(1)请写出图(2)所表示的代数恒等式:__________;
(2)请写出图(3)所表示的代数恒等式:__________;
(3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2.
思路分析:这实际上是一种图形的两种面积表示方法,所以它们是相等的.计算面积时,列出的是整式的乘法.
解:(1)(x+y)(2x+y)=2x2+3xy+y2
(2)(2x+y)(x+2y)=2x2+5xy+2y2
(3)答案不唯一,如图:
( http: / / www.21cnjy.com )
10.如图15-3-3所示,长方形AB ( http: / / www.21cnjy.com )CD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求长方形ABCD中最大正方形与最小正方形的面积之差.
( http: / / www.21cnjy.com )
图15-3-3
思路分析:因为小正方形的面积为4, ( http: / / www.21cnjy.com )所以它的边长为2.显然它是最小的正方形.其余正方形的边长是b=a+2,c=b+2=a+4,d=c+2=a+6,可见边长为d的正方形是最大的,因此可求得两正方形面积差.
解:由题意,得b=a+2,c=b+2=a+4,d=c+2=a+6,
∵AB=DC,∴d+c=b+2a.
∴a+6+a+4=a+2+2a.∴a=8.
∴两正方形的面积差为d2-4=(a+6)2-4=(8+6)2-4=192.
