5.2.1三角函数的概念 课件(共33张PPT)
文档属性
| 名称 | 5.2.1三角函数的概念 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 46.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 17:27:10 | ||
图片预览










文档简介
(共33张PPT)
第 5 章 三角函数
人教A版2019必修第一册
5.2.1 三角函数的概念
01.
三角函数的定义
02.
三角函数的正负
目录
03.
诱导公式一
学习目标
1.借助单位圆理解任意角三角函数的定义.
2.掌握任意角三角函数在各象限的符号.
3.掌握并应用公式解决问题.
Topic. 01
01 复习导入
y
x
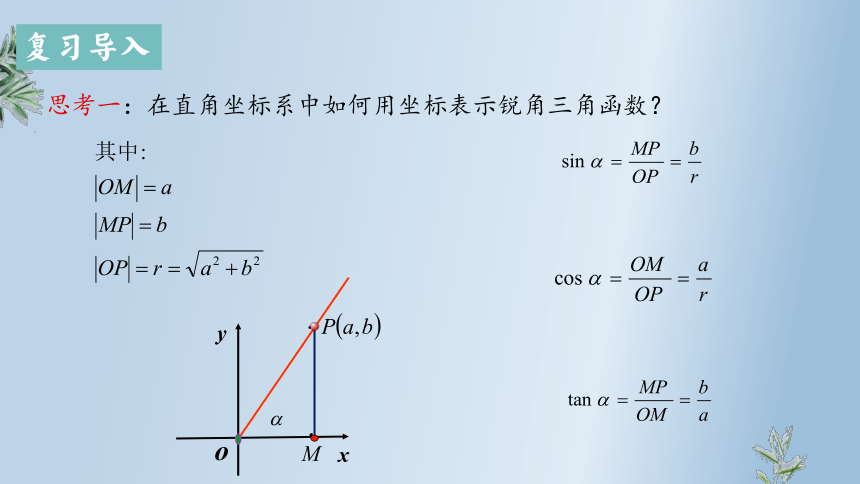
思考一:在直角坐标系中如何用坐标表示锐角三角函数?
﹒
﹒
o
复习导入
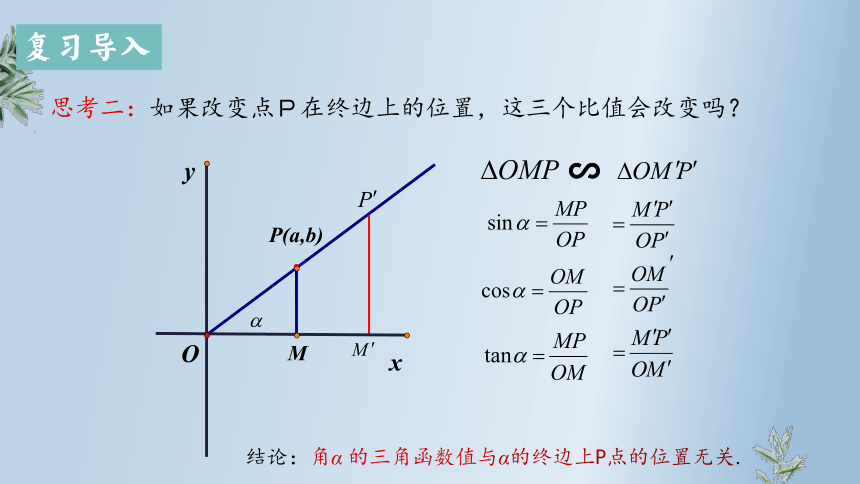
思考二:如果改变点P在终边上的位置,这三个比值会改变吗?
﹒
∽
M
O
y
x
P(a,b)
结论:角α 的三角函数值与α的终边上P点的位置无关.
复习导入
Topic. 02
02 三角函数的概念
三角函数的概念
在弧度制下,我们已经将角的范围扩展到全体实数,下面借助这些知识研究上一节开头提出的问题,不失一般性,先研究单位圆上点的运动.现在的任务是:
如图,单位圆上⊙O的点P以A为起点做逆时针方向旋转,建立一个数学模型,刻画点P的位置变化情况.
我们利用直角坐标系来研究上述问题.
如图,以单位圆的圆心为原点, 以射线OA为x轴的非负半轴,建立直角坐标系.则A(1,0),P(x,y),射线OA从x非负半轴开始,绕点O按逆时针方向旋转角α,终止位置为OP.
三角函数的概念
三角函数的概念
探究:当时,点P的坐标是什么?
当或时,点P的坐标又是什么?它们是唯一确定的吗?
当时,点P
当时,点P
当时,点P
它们是唯一确定的。
三角函数的概念
设α是一个任意角,α∈R,它的终边OP与单位圆相交于P(x,y)
正弦函数
把点P的纵坐标y叫做α的正弦函数,记作sinα,即 y=sinα
余弦函数
把点P的横坐标x叫做α的余弦函数,记作cosα,即 x=cosα
正切函数
把点P的纵坐标与横坐标的比值叫做α的正切,记作tanα,即
三角函数的概念
我们将正弦函数、余弦函数和正切函数统称为三角函数
(trigonometic function),通常将它们记为:
三角函数
正弦函数 y=sinx,xR
余弦函数 y=cosx,xR
正切函数
角
实数
(角的弧度)
三角
函数值
三角函数的概念
三角函数定义推广
设角α是一个任意角,P(x,y)是终边上的任意一点,
点P与原点的距离
三角函数的概念
三角函数
定义域
R
R
在弧度制下,三角函数的定义域:
三角函数的概念
1.求的正弦、余弦和正切值.
的终边与单位圆的交点坐标为
解:在直角坐标系中,作
所以
三角函数的概念
2. 在平面直角坐标系中,角α的终边与单位圆交于点A,点A的纵坐标为,求tanα.
常见角的三角函数值
无
三角函数的概念
三角函数的概念
A
.
.
.
4. 已知角α的终边在直线y=x上,求sin α,cos α,tan α的值.
三角函数的概念
Topic. 03
03 三角函数的正负
三角函数正负
思考: 根据任意角三角函数的定义,sinα,cosα,tanα的值的符号取决于什么?
-
+
+
+
+
+
-
-
-
-
-
+
y
O
x
O
x
y
O
x
y
三角函数正负
x
y
O
三角函数全为正
正弦为正
正切为正
余弦为正
三角函数值的符号问题
一正二正弦,三切四余弦
三角函数正负
1. 下列各式为正号的是( )
A. cos2 B. cos2 sin2 C. tan2 cos2 D. sin2 tan2
C
2.
D
B
三角函数正负
3.确定下列三角函数的符号
(1)sin250° (2)tan(-672°) (3)tan3π
三角函数正负
判断三角函数值在各象限符号的攻略:(1)基础:准确确定三角函数值中各角所在象限;(2)关键:准确记忆三角函数在各象限的符号;(3)注意:用弧度制给出的角常常不写单位,不要误认为角度导致象限判断错误.
提醒:注意巧用口诀记忆三角函数值在各象限符号.
方法总结
由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等.
由此得到一组公式:
诱导公式一
利用公式一,可以把求任意角的三角函数值,转化为求0~2π(或0°~360°)角的三角函数值
4. 求下列三角函数值:
(1) (2)
解:(1)
(2)
诱导公式一
(1)定形:将已知的任意角写成2kπ+α的形式,其中α∈[0,2π),k∈Z.(2)转化:根据诱导公式,转化为求角α的某个三角函数值.(3)求值:若角为特殊角,可直接求出该角的三角函数值.
方法总结
诱导公式一
诱导公式一
5.求下列三角函数值
(1) (2) (3)
诱导公式一
6.求下列三角函数值
(1) (2) (3)
Topic. 04
04 课堂小结
课堂小结
总结:
1.三角函数的定义。
2.三角函数的正负。
3.诱导公式一。
感谢观看
第 5 章 三角函数
人教A版2019必修第一册
5.2.1 三角函数的概念
01.
三角函数的定义
02.
三角函数的正负
目录
03.
诱导公式一
学习目标
1.借助单位圆理解任意角三角函数的定义.
2.掌握任意角三角函数在各象限的符号.
3.掌握并应用公式解决问题.
Topic. 01
01 复习导入
y
x
思考一:在直角坐标系中如何用坐标表示锐角三角函数?
﹒
﹒
o
复习导入
思考二:如果改变点P在终边上的位置,这三个比值会改变吗?
﹒
∽
M
O
y
x
P(a,b)
结论:角α 的三角函数值与α的终边上P点的位置无关.
复习导入
Topic. 02
02 三角函数的概念
三角函数的概念
在弧度制下,我们已经将角的范围扩展到全体实数,下面借助这些知识研究上一节开头提出的问题,不失一般性,先研究单位圆上点的运动.现在的任务是:
如图,单位圆上⊙O的点P以A为起点做逆时针方向旋转,建立一个数学模型,刻画点P的位置变化情况.
我们利用直角坐标系来研究上述问题.
如图,以单位圆的圆心为原点, 以射线OA为x轴的非负半轴,建立直角坐标系.则A(1,0),P(x,y),射线OA从x非负半轴开始,绕点O按逆时针方向旋转角α,终止位置为OP.
三角函数的概念
三角函数的概念
探究:当时,点P的坐标是什么?
当或时,点P的坐标又是什么?它们是唯一确定的吗?
当时,点P
当时,点P
当时,点P
它们是唯一确定的。
三角函数的概念
设α是一个任意角,α∈R,它的终边OP与单位圆相交于P(x,y)
正弦函数
把点P的纵坐标y叫做α的正弦函数,记作sinα,即 y=sinα
余弦函数
把点P的横坐标x叫做α的余弦函数,记作cosα,即 x=cosα
正切函数
把点P的纵坐标与横坐标的比值叫做α的正切,记作tanα,即
三角函数的概念
我们将正弦函数、余弦函数和正切函数统称为三角函数
(trigonometic function),通常将它们记为:
三角函数
正弦函数 y=sinx,xR
余弦函数 y=cosx,xR
正切函数
角
实数
(角的弧度)
三角
函数值
三角函数的概念
三角函数定义推广
设角α是一个任意角,P(x,y)是终边上的任意一点,
点P与原点的距离
三角函数的概念
三角函数
定义域
R
R
在弧度制下,三角函数的定义域:
三角函数的概念
1.求的正弦、余弦和正切值.
的终边与单位圆的交点坐标为
解:在直角坐标系中,作
所以
三角函数的概念
2. 在平面直角坐标系中,角α的终边与单位圆交于点A,点A的纵坐标为,求tanα.
常见角的三角函数值
无
三角函数的概念
三角函数的概念
A
.
.
.
4. 已知角α的终边在直线y=x上,求sin α,cos α,tan α的值.
三角函数的概念
Topic. 03
03 三角函数的正负
三角函数正负
思考: 根据任意角三角函数的定义,sinα,cosα,tanα的值的符号取决于什么?
-
+
+
+
+
+
-
-
-
-
-
+
y
O
x
O
x
y
O
x
y
三角函数正负
x
y
O
三角函数全为正
正弦为正
正切为正
余弦为正
三角函数值的符号问题
一正二正弦,三切四余弦
三角函数正负
1. 下列各式为正号的是( )
A. cos2 B. cos2 sin2 C. tan2 cos2 D. sin2 tan2
C
2.
D
B
三角函数正负
3.确定下列三角函数的符号
(1)sin250° (2)tan(-672°) (3)tan3π
三角函数正负
判断三角函数值在各象限符号的攻略:(1)基础:准确确定三角函数值中各角所在象限;(2)关键:准确记忆三角函数在各象限的符号;(3)注意:用弧度制给出的角常常不写单位,不要误认为角度导致象限判断错误.
提醒:注意巧用口诀记忆三角函数值在各象限符号.
方法总结
由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等.
由此得到一组公式:
诱导公式一
利用公式一,可以把求任意角的三角函数值,转化为求0~2π(或0°~360°)角的三角函数值
4. 求下列三角函数值:
(1) (2)
解:(1)
(2)
诱导公式一
(1)定形:将已知的任意角写成2kπ+α的形式,其中α∈[0,2π),k∈Z.(2)转化:根据诱导公式,转化为求角α的某个三角函数值.(3)求值:若角为特殊角,可直接求出该角的三角函数值.
方法总结
诱导公式一
诱导公式一
5.求下列三角函数值
(1) (2) (3)
诱导公式一
6.求下列三角函数值
(1) (2) (3)
Topic. 04
04 课堂小结
课堂小结
总结:
1.三角函数的定义。
2.三角函数的正负。
3.诱导公式一。
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
