人教版数学八年级上册 12.1全等三角形 课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.1全等三角形 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 860.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 13:25:05 | ||
图片预览


文档简介
(共17张PPT)
第十二章 全等三角形
12.1 全等三角形
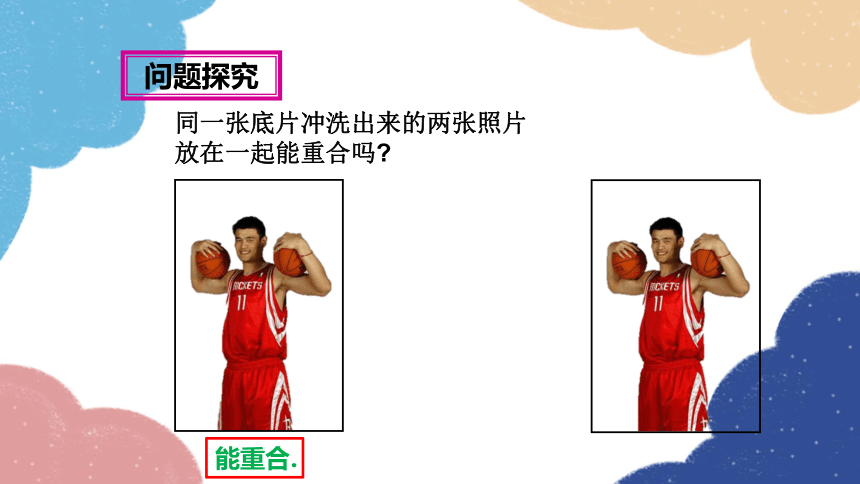
同一张底片冲洗出来的两张照片
放在一起能重合吗
问题探究
能重合.
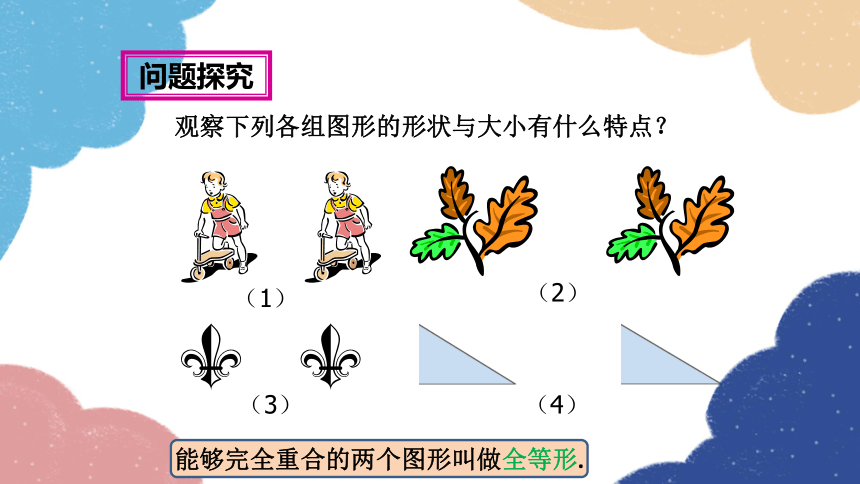
观察下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
能够完全重合的两个图形叫做全等形.
问题探究
只有形状
相同
只有大小
相同
观察下面两组图形,它们是不是全等形?
( 1 )
( 2 )
全等形的形状和大小都相同.
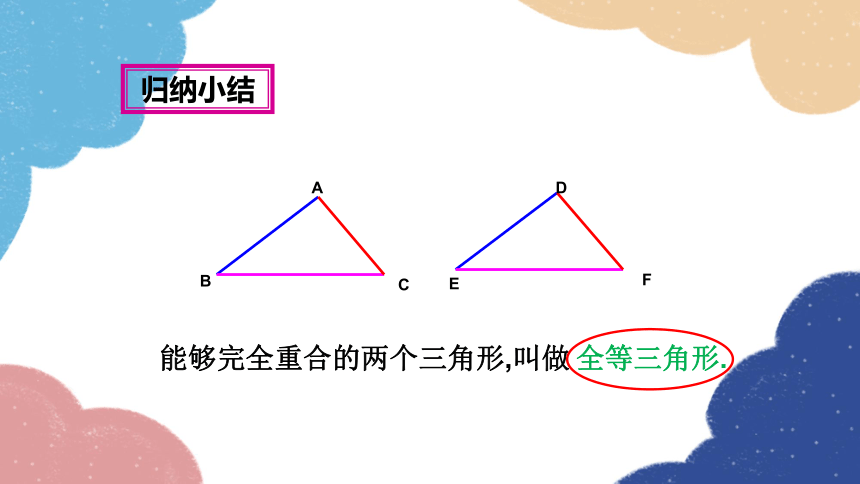
问题探究
A
B
C
E
D
F
能够完全重合的两个三角形,叫做
全等三角形.
归纳小结
D
C
O
A
B
A
B
C
D
E
F
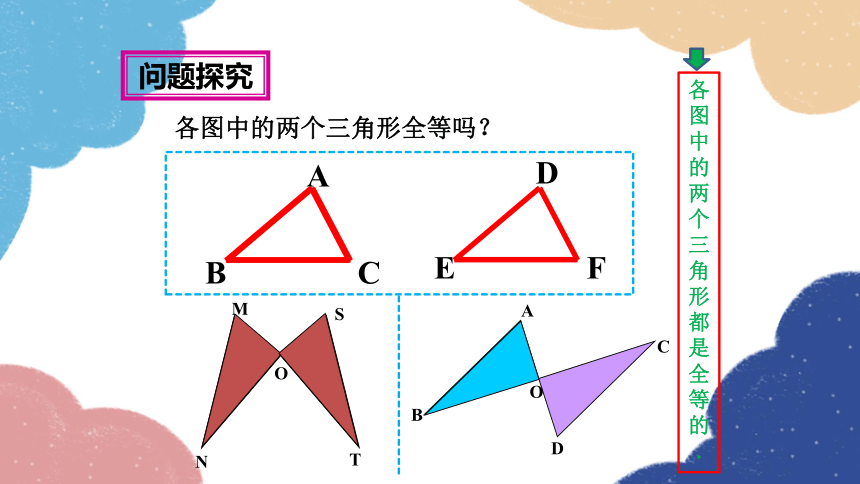
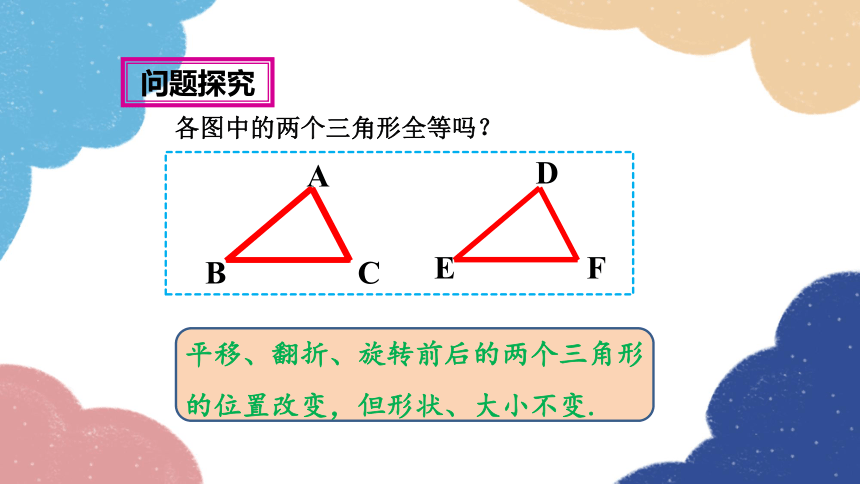
各图中的两个三角形全等吗?
N
M
S
O
T
问题探究
各图中的两个三角形都是全等的
.
平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变.
各图中的两个三角形全等吗?
问题探究
A
B
C
D
E
F
A
B
C
D
E
F
如果△ABC与△DEF会互相重合,顶点A与顶点 重合,
顶点B与顶点 重合,顶点C与顶点 重合.
AB边与边 重合, BC边与 边重合,AC边
与 边重合.
∠A与 重合,∠B与 重合,∠C与 重合.
D
E
F
DE
EF
DF
∠D
∠E
∠F
新知学习
重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
A
B
C
D
E
F
读作“全等于”.
“全等”用符号“ ”来表示,
≌
注意:通常对应顶点的字母写在对应位置上.
≌
△ABC
△DEF .
记作:
新知学习
≌
全等三角形的对应边相等、对应角相等.
全等三角形的性质:
A
A′
B
B′
C
C′
△
△
思考:
△ABC≌△A′B′C′,对应边有什么关系?对应角呢?
新知学习
A
B
C
A′
B′
C′
对应边相等、对应角相等.
新知运用
1、若△AOC≌△BOD,AC= ,
∠A= .
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA= .
3、若△ABC≌△CDA, AB= ,
∠BAC= .
A
B
C
D
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
1、有公共边:
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点:
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
探索规律
寻找对应边、对应角的规律.
1、有公共边:
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点:
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
探索规律
寻找对应边、对应角的规律.
在全等三角形中,规律一般是:
1、有公共边,则公共边为对应边;
2、有公共角,则公共角为对应角(对顶角为对应角);
3、最长边与最长边(最短边与最短边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
4、对应角的对边为对应边;对应边的对角为对应角;
5、根据书写规范,按照对应顶点找对应边或对应角.
规律总结
A
D
C
B
A
E
B
D
C
A
B
C
D
E
F
(2)已知△ABC≌△CDA,
则AC边的对应边为 .
(1)已知△ABC≌△ADE,
则∠A的对应角为 .
(3)已知△ ABC ≌△DEF,
则AB边的对应边为 .
∠C的对应角为 .
CA
∠A
DE
∠F
随堂练习
(4)如右图,已知△ABD≌△ACE,
且∠C=45°,AC = 8,AE = 5,则
∠B = , DC = .
A
E
B
C
D
8
5
5
45°
3
随堂练习
(5) △ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=6cm,BD=5cm,AD=7cm,那么BC的长是( )
(A)7cm (B)6cm (C)5cm ( D)无法确定
A
A
C
D
B
归纳总结
1.全等(三角形)形的概念:
能够完全重合的两个图形叫做全等形;
能够完全重合的两个三角形,叫做全等三角形.
2.全等三角形的性质:
对应边相等、对应角相等.
3.会识别全等三角形的对应边、对应角.
第十二章 全等三角形
12.1 全等三角形
同一张底片冲洗出来的两张照片
放在一起能重合吗
问题探究
能重合.
观察下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
能够完全重合的两个图形叫做全等形.
问题探究
只有形状
相同
只有大小
相同
观察下面两组图形,它们是不是全等形?
( 1 )
( 2 )
全等形的形状和大小都相同.
问题探究
A
B
C
E
D
F
能够完全重合的两个三角形,叫做
全等三角形.
归纳小结
D
C
O
A
B
A
B
C
D
E
F
各图中的两个三角形全等吗?
N
M
S
O
T
问题探究
各图中的两个三角形都是全等的
.
平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变.
各图中的两个三角形全等吗?
问题探究
A
B
C
D
E
F
A
B
C
D
E
F
如果△ABC与△DEF会互相重合,顶点A与顶点 重合,
顶点B与顶点 重合,顶点C与顶点 重合.
AB边与边 重合, BC边与 边重合,AC边
与 边重合.
∠A与 重合,∠B与 重合,∠C与 重合.
D
E
F
DE
EF
DF
∠D
∠E
∠F
新知学习
重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
A
B
C
D
E
F
读作“全等于”.
“全等”用符号“ ”来表示,
≌
注意:通常对应顶点的字母写在对应位置上.
≌
△ABC
△DEF .
记作:
新知学习
≌
全等三角形的对应边相等、对应角相等.
全等三角形的性质:
A
A′
B
B′
C
C′
△
△
思考:
△ABC≌△A′B′C′,对应边有什么关系?对应角呢?
新知学习
A
B
C
A′
B′
C′
对应边相等、对应角相等.
新知运用
1、若△AOC≌△BOD,AC= ,
∠A= .
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA= .
3、若△ABC≌△CDA, AB= ,
∠BAC= .
A
B
C
D
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
1、有公共边:
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点:
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
探索规律
寻找对应边、对应角的规律.
1、有公共边:
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点:
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
探索规律
寻找对应边、对应角的规律.
在全等三角形中,规律一般是:
1、有公共边,则公共边为对应边;
2、有公共角,则公共角为对应角(对顶角为对应角);
3、最长边与最长边(最短边与最短边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
4、对应角的对边为对应边;对应边的对角为对应角;
5、根据书写规范,按照对应顶点找对应边或对应角.
规律总结
A
D
C
B
A
E
B
D
C
A
B
C
D
E
F
(2)已知△ABC≌△CDA,
则AC边的对应边为 .
(1)已知△ABC≌△ADE,
则∠A的对应角为 .
(3)已知△ ABC ≌△DEF,
则AB边的对应边为 .
∠C的对应角为 .
CA
∠A
DE
∠F
随堂练习
(4)如右图,已知△ABD≌△ACE,
且∠C=45°,AC = 8,AE = 5,则
∠B = , DC = .
A
E
B
C
D
8
5
5
45°
3
随堂练习
(5) △ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=6cm,BD=5cm,AD=7cm,那么BC的长是( )
(A)7cm (B)6cm (C)5cm ( D)无法确定
A
A
C
D
B
归纳总结
1.全等(三角形)形的概念:
能够完全重合的两个图形叫做全等形;
能够完全重合的两个三角形,叫做全等三角形.
2.全等三角形的性质:
对应边相等、对应角相等.
3.会识别全等三角形的对应边、对应角.
