第三章 3.2.1 函数单调性与最大(小)值第1课时函数单调性 课件(共28张PPT)
文档属性
| 名称 | 第三章 3.2.1 函数单调性与最大(小)值第1课时函数单调性 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 10:41:17 | ||
图片预览



文档简介
(共28张PPT)
第三章
3.2.1函数单调性与最大(小)值第1课时 函数单调性
人教A版(2019)
教学目标
学习目标 数学素养
1.了解函数单调性和单调区间的概 念,掌握判断一些简单函数单调性和 单调区间的方法. 1.培养学生的直观想象及数学抽象素养.
2.理解函数单调性的本质特征,能正确应用函数单调性的定义证明函数的单调性. 2.培养学生逻辑推理及数学运算素养.
3.会根据函数单调性的定义和运用函数图像探求一些简单函数的单调区间. 3.培养学生的数学抽象和数学运算素养.
情景引入
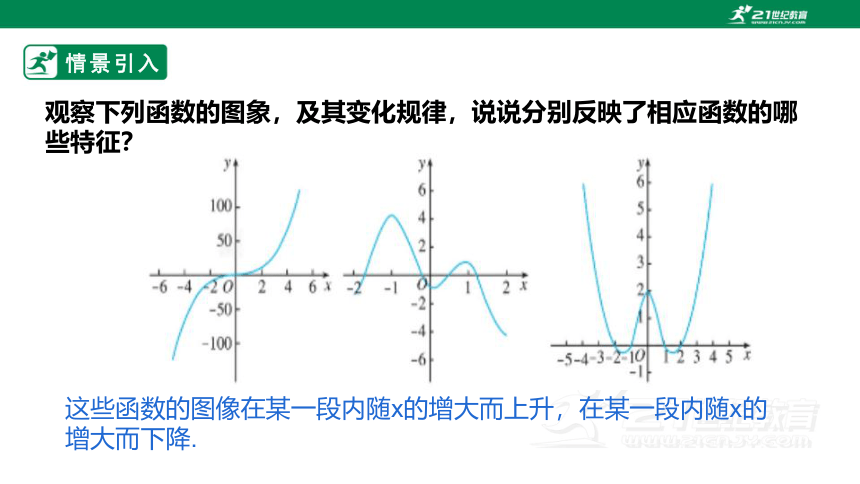
观察下列函数的图象,及其变化规律,说说分别反映了相应函数的哪些特征?
这些函数的图像在某一段内随x的增大而上升,在某一段内随x的增大而下降.
知新初探
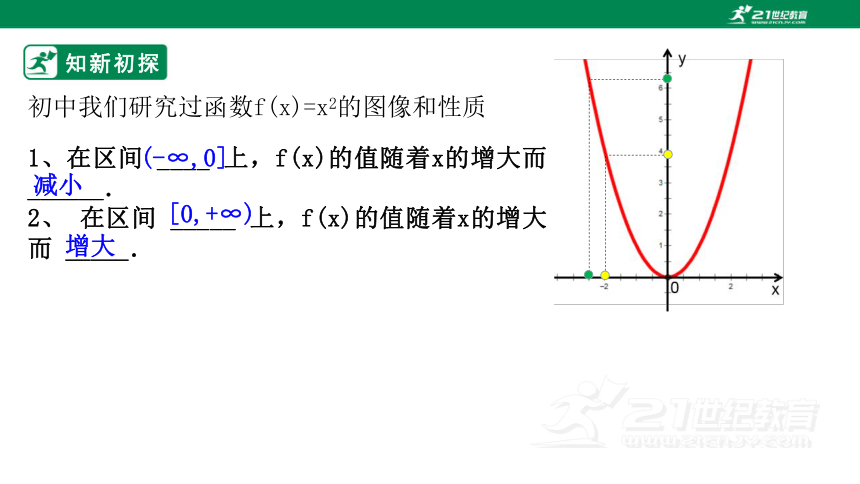
初中我们研究过函数f(x)=x2的图像和性质
1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____.
(-∞,0]
减小
[0,+∞)
增大
知新探究
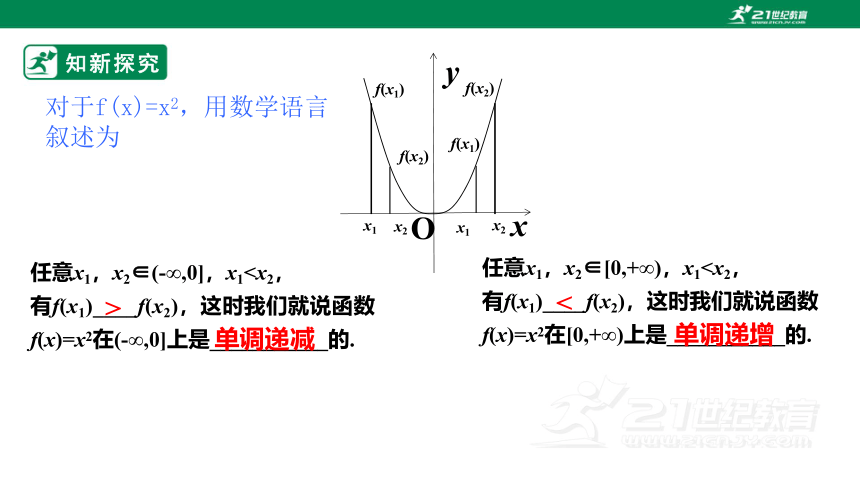
对于f(x)=x2,用数学语言叙述为
x
O
f(x2)
f(x1)
x1
x2
f(x2)
x1
x2
f(x1)
y
任意x1,x2∈(-∞,0],x1有f(x1)____f(x2),这时我们就说函数f(x)=x2在(-∞,0]上是___________的.
任意x1,x2∈[0,+∞),x1有f(x1)____f(x2),这时我们就说函数f(x)=x2在[0,+∞)上是___________的.
>
单调递减
<
单调递增
5
新知探究
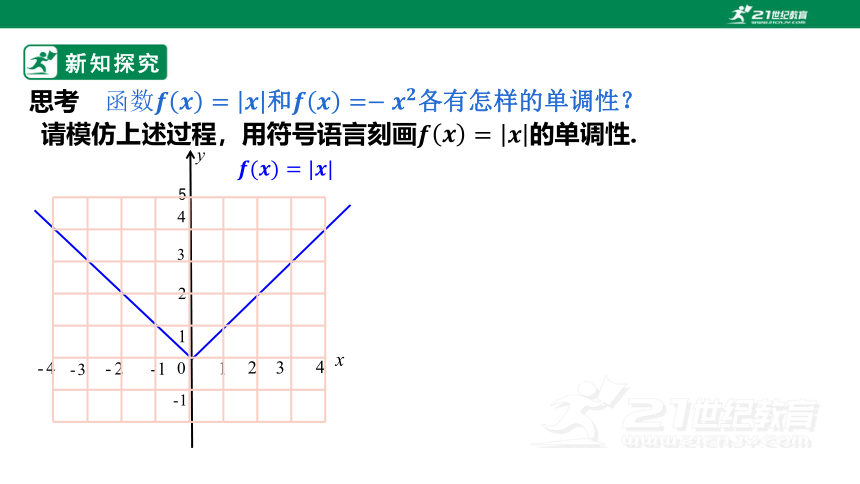
和各有怎样的单调性?
思考
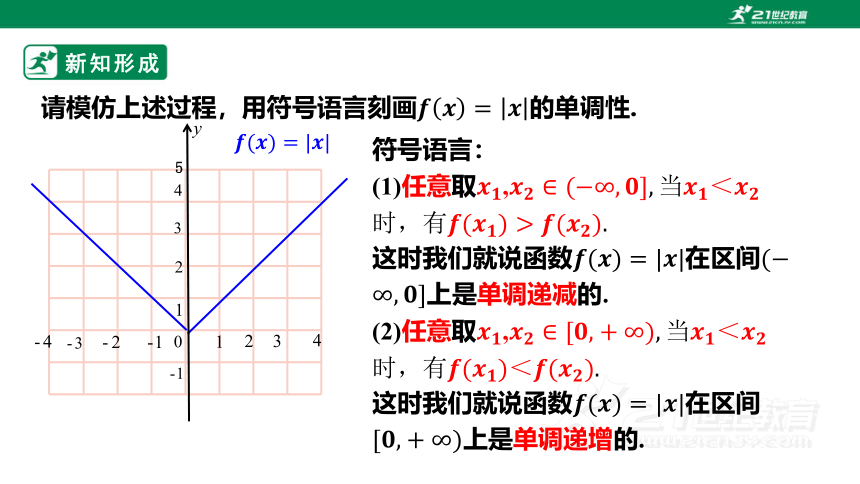
请模仿上述过程,用符号语言刻画的单调性.
新知形成
请模仿上述过程,用符号语言刻画的单调性.
5
符号语言:
(1)任意取,
这时我们就说函数在区间上是单调递减的.
(2)任意取,
这时我们就说函数在区间上是单调递增的.
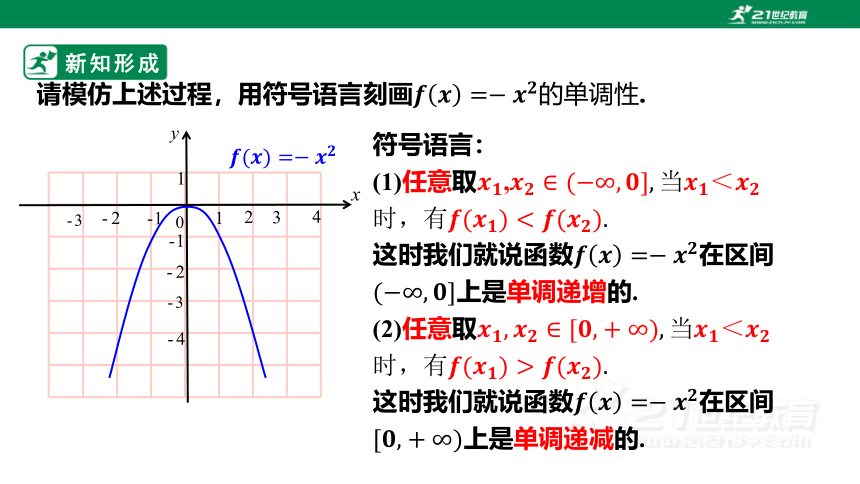
新知形成
请模仿上述过程,用符号语言刻画.
符号语言:
(1)任意取,
这时我们就说函数在区间上是单调递增的.
(2)任意取
这时我们就说函数在区间上是单调递减的.
新知讲解
一般地,设函数的定义域为,区间 D:
如果 ,当时,都有,那么就称函数在区间上单调递增.(如右图)
O
x
y
x1
f(x1)
f(x2)
x2
特别地,当函数在它的定义域上单调递增时,我们就称它是增函数.
如果 ,当时,都有,那么就称函数在区间上单调递减.(如右图)
特别地,当函数在它的定义域上单调递减时,
我们就称它是减函数.
x
O
y
x1
x2
f(x1)
f(x2)
如果函数 y =f(x)在区间单调递增或单调递减,那么就说函数 y =f(x)在这一区间上具有(严格的)单调性,区间叫做y =f(x)的单调区间
新知讲解
思考
新知讲解
新知讲解
1.如果函数f(x)的的定义域为D,区间I D,对于 x1,x2∈I,x1,则函数f(x)在区间I上 .
2.如果函数f(x)的的定义域为D,区间I D,对于 x1,x2∈I,x1,则函数f(x)在区间I上 .
单调递增
单调递减
思考
新知讲解
注意:
(1)函数的单调性也叫函数的增减性.
(2)函数的单调性是对某个区间而言的,它是个局部概念.这个区间是定义域的子集.
(3)单调区间:针对自变量 x 而言的.
若函数在此区间上是单调递增,则区间为单调递增区间
若函数在此区间上是单调递减,则区间为单调递减区间
(4)单调函数的图像特征(几何特征):
单调递增 图像从左向右上升
单调递减 图像从左向右下降
新知讲解
思考
函数的单调性是对定义域上的某个区间而言的,你能举出在整个定义域内单调递增的函数吗?你能举出在定义域内的某些区间单调递增但在另一些区间上单调递减的函数吗?
x
y
O
x
y
O
增函数、减函数是针对的函数的整个定义域,是函数的整体性质,
而函数的单调性是对定义域下的某个区间而言的,是函数的局部性质.
一个函数在定义域下的某个区间具有单调性,但在整个定义域上不一定具有单调性.
新知探究
如何描述函数的单调性?
思考
f(x)在(-∞,0)上单调递减 f(x)在定义域(∞,0)∪(0,+∞)上单调递减
f(x)在(0,+∞)上单调递减
√ ×
单调递减区间为(-∞,0),(0,+∞)
注意:单调区间一般不能取并集,
应该用“和”或“,”连接
问题探究
【例1】根据定义,研究函数f(x)=kx+b(k≠0)的单调性.
分析:根据函数单调性的定义,需要考察当x1f(x2).根据实数大小关系的基本事实,只要考察f(x1)-f(x2)与0的大小关系
问题探究
【例1】根据定义,研究函数f(x)=kx+b(k≠0)的单调性.
证明: x1,x2∈R且x1f(x1)-f(x2)=(kx1+b)-(kx2+b)=k(x1-x2)
由x1得x1-x2<0
当k>0时,
k(x1-x2)<0,
∴f(x1)-f(x2)<0,即f(x1)∴这时函数f(x)=kx+b是增函数.
当k<0时, k(x1-x2)>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴这时函数f(x)=kx+b是减函数.
作差法
为了定号,所以因式分解
取值
作差
变形
定号
结论
方法总结
【方法规律】
利用定义判断与证明函数单调性的4个步骤:
新知讲解
学生活动:板书10分钟
【例2】物理学中的玻意耳定律 (k 为正常数)告诉我们,对于一定量的气体,当其体积V减小时,压强 p 将增大.试对此用函数的单调性证明.
【例3】根据定义证明函数 在区间(1,+∞)上单调递增.
新知讲解
【例2】物理学中的玻意耳定律 (k 为正常数)告诉我们,对于一定量的气体,当其体积V减小时,压强 p 将增大.试对此用函数的单调性证明.
取值
证明:定义域为(0,+∞), V1,V2∈(0,+∞)且V1作差
变形
数学运算
彻底因式分解
定号
∵V1,V2∈(0,+∞),
∴V1V2>0,
∴V2-V1>0,
∵V1∴p1-p2>0,即p1>p2.
又k>0,
结论
∴函数 是(0,+∞)上的减函数.即当体积V减小时,压强 p将增大.
新知讲解
【例3】根据定义证明函数 在区间(1,+∞)上单调递增.
取值
证明: x1,x2∈(1,+∞)且x1作差
变形
定号
∵x1,x2∈(1,+∞),
∴x1>1, x2>1,∴x1x2>1, x1x2-1>0
又x1∴x1-x2<0,
∴ ,即y1结论
∴函数 在区间(1,+∞)上单调递增.
新知讲解
【拓展延申】根据定义证明函数 在区间(0,1)上单调递减.
取值
证明: x1,x2∈(0,1)且x1作差
变形
定号
∵x1,x2∈(0,1),
∴0又x1∴x1-x2<0,
∴ ,即y1>y2
结论
∴函数 在区间(0,1)上单调递减.
初试身手
p79 练习 2,3
⑴求y= -x+5的单调区间;
⑵求y= -x2+3x+5的单调区间.
课堂总结
1.什么是函数的单调性?什么是单调递增,单调递减,增函数、减函数?
2.理解函数的单调性时应把握好哪一些问题?
3.通过本节的学习,你认为可以如何判定函数的单调性?
(1)图象法(直观判断);(2)定义法(严格推导).
4.通过本节的学习,你对函数性质的研究方法有什么体会?
具体函数→图象特征(定性刻画) →数量刻画(定量刻画)→数学符号语言 →抽象出单调性的一般定 →判定具体函数的单调性
作业布置
作业: p85-86 习题3.1 1,2,3,8.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第三章
3.2.1函数单调性与最大(小)值第1课时 函数单调性
人教A版(2019)
教学目标
学习目标 数学素养
1.了解函数单调性和单调区间的概 念,掌握判断一些简单函数单调性和 单调区间的方法. 1.培养学生的直观想象及数学抽象素养.
2.理解函数单调性的本质特征,能正确应用函数单调性的定义证明函数的单调性. 2.培养学生逻辑推理及数学运算素养.
3.会根据函数单调性的定义和运用函数图像探求一些简单函数的单调区间. 3.培养学生的数学抽象和数学运算素养.
情景引入
观察下列函数的图象,及其变化规律,说说分别反映了相应函数的哪些特征?
这些函数的图像在某一段内随x的增大而上升,在某一段内随x的增大而下降.
知新初探
初中我们研究过函数f(x)=x2的图像和性质
1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____.
(-∞,0]
减小
[0,+∞)
增大
知新探究
对于f(x)=x2,用数学语言叙述为
x
O
f(x2)
f(x1)
x1
x2
f(x2)
x1
x2
f(x1)
y
任意x1,x2∈(-∞,0],x1
任意x1,x2∈[0,+∞),x1
>
单调递减
<
单调递增
5
新知探究
和各有怎样的单调性?
思考
请模仿上述过程,用符号语言刻画的单调性.
新知形成
请模仿上述过程,用符号语言刻画的单调性.
5
符号语言:
(1)任意取,
这时我们就说函数在区间上是单调递减的.
(2)任意取,
这时我们就说函数在区间上是单调递增的.
新知形成
请模仿上述过程,用符号语言刻画.
符号语言:
(1)任意取,
这时我们就说函数在区间上是单调递增的.
(2)任意取
这时我们就说函数在区间上是单调递减的.
新知讲解
一般地,设函数的定义域为,区间 D:
如果 ,当时,都有,那么就称函数在区间上单调递增.(如右图)
O
x
y
x1
f(x1)
f(x2)
x2
特别地,当函数在它的定义域上单调递增时,我们就称它是增函数.
如果 ,当时,都有,那么就称函数在区间上单调递减.(如右图)
特别地,当函数在它的定义域上单调递减时,
我们就称它是减函数.
x
O
y
x1
x2
f(x1)
f(x2)
如果函数 y =f(x)在区间单调递增或单调递减,那么就说函数 y =f(x)在这一区间上具有(严格的)单调性,区间叫做y =f(x)的单调区间
新知讲解
思考
新知讲解
新知讲解
1.如果函数f(x)的的定义域为D,区间I D,对于 x1,x2∈I,x1
2.如果函数f(x)的的定义域为D,区间I D,对于 x1,x2∈I,x1
单调递增
单调递减
思考
新知讲解
注意:
(1)函数的单调性也叫函数的增减性.
(2)函数的单调性是对某个区间而言的,它是个局部概念.这个区间是定义域的子集.
(3)单调区间:针对自变量 x 而言的.
若函数在此区间上是单调递增,则区间为单调递增区间
若函数在此区间上是单调递减,则区间为单调递减区间
(4)单调函数的图像特征(几何特征):
单调递增 图像从左向右上升
单调递减 图像从左向右下降
新知讲解
思考
函数的单调性是对定义域上的某个区间而言的,你能举出在整个定义域内单调递增的函数吗?你能举出在定义域内的某些区间单调递增但在另一些区间上单调递减的函数吗?
x
y
O
x
y
O
增函数、减函数是针对的函数的整个定义域,是函数的整体性质,
而函数的单调性是对定义域下的某个区间而言的,是函数的局部性质.
一个函数在定义域下的某个区间具有单调性,但在整个定义域上不一定具有单调性.
新知探究
如何描述函数的单调性?
思考
f(x)在(-∞,0)上单调递减 f(x)在定义域(∞,0)∪(0,+∞)上单调递减
f(x)在(0,+∞)上单调递减
√ ×
单调递减区间为(-∞,0),(0,+∞)
注意:单调区间一般不能取并集,
应该用“和”或“,”连接
问题探究
【例1】根据定义,研究函数f(x)=kx+b(k≠0)的单调性.
分析:根据函数单调性的定义,需要考察当x1
问题探究
【例1】根据定义,研究函数f(x)=kx+b(k≠0)的单调性.
证明: x1,x2∈R且x1
由x1
当k>0时,
k(x1-x2)<0,
∴f(x1)-f(x2)<0,即f(x1)
当k<0时, k(x1-x2)>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴这时函数f(x)=kx+b是减函数.
作差法
为了定号,所以因式分解
取值
作差
变形
定号
结论
方法总结
【方法规律】
利用定义判断与证明函数单调性的4个步骤:
新知讲解
学生活动:板书10分钟
【例2】物理学中的玻意耳定律 (k 为正常数)告诉我们,对于一定量的气体,当其体积V减小时,压强 p 将增大.试对此用函数的单调性证明.
【例3】根据定义证明函数 在区间(1,+∞)上单调递增.
新知讲解
【例2】物理学中的玻意耳定律 (k 为正常数)告诉我们,对于一定量的气体,当其体积V减小时,压强 p 将增大.试对此用函数的单调性证明.
取值
证明:定义域为(0,+∞), V1,V2∈(0,+∞)且V1
变形
数学运算
彻底因式分解
定号
∵V1,V2∈(0,+∞),
∴V1V2>0,
∴V2-V1>0,
∵V1
又k>0,
结论
∴函数 是(0,+∞)上的减函数.即当体积V减小时,压强 p将增大.
新知讲解
【例3】根据定义证明函数 在区间(1,+∞)上单调递增.
取值
证明: x1,x2∈(1,+∞)且x1
变形
定号
∵x1,x2∈(1,+∞),
∴x1>1, x2>1,∴x1x2>1, x1x2-1>0
又x1
∴ ,即y1
∴函数 在区间(1,+∞)上单调递增.
新知讲解
【拓展延申】根据定义证明函数 在区间(0,1)上单调递减.
取值
证明: x1,x2∈(0,1)且x1
变形
定号
∵x1,x2∈(0,1),
∴0
∴ ,即y1>y2
结论
∴函数 在区间(0,1)上单调递减.
初试身手
p79 练习 2,3
⑴求y= -x+5的单调区间;
⑵求y= -x2+3x+5的单调区间.
课堂总结
1.什么是函数的单调性?什么是单调递增,单调递减,增函数、减函数?
2.理解函数的单调性时应把握好哪一些问题?
3.通过本节的学习,你认为可以如何判定函数的单调性?
(1)图象法(直观判断);(2)定义法(严格推导).
4.通过本节的学习,你对函数性质的研究方法有什么体会?
具体函数→图象特征(定性刻画) →数量刻画(定量刻画)→数学符号语言 →抽象出单调性的一般定 →判定具体函数的单调性
作业布置
作业: p85-86 习题3.1 1,2,3,8.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
