人教版数学八年级上册 13.4课题学习最短路径问题 课件(共11张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.4课题学习最短路径问题 课件(共11张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 408.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 15:52:50 | ||
图片预览


文档简介
(共11张PPT)
13.4 课题学习
最短路径问题
草地
河
B
A
牧马人
营地
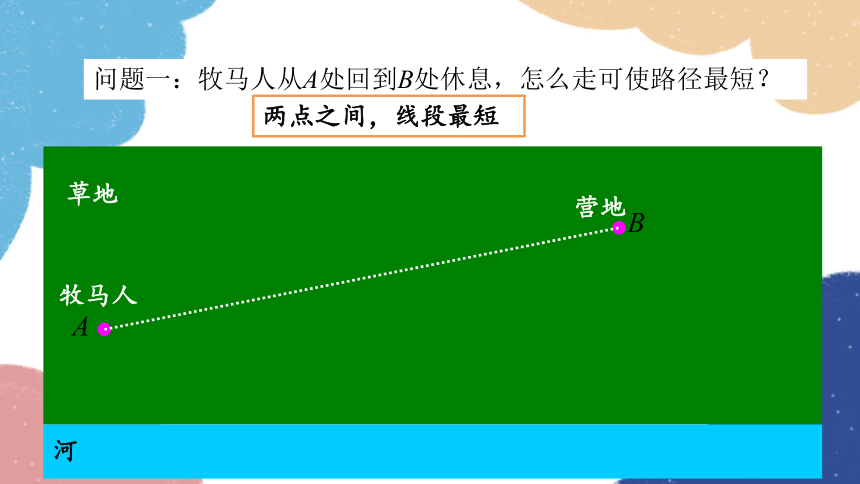
问题一:牧马人从A处回到B处休息,怎么走可使路径最短?
两点之间,线段最短
草地
河
B
A
牧马人
营地
l
D
问题二:牧马人从A处到河边 l 处饮马,怎么走可使路径最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短
草地
河
A
B
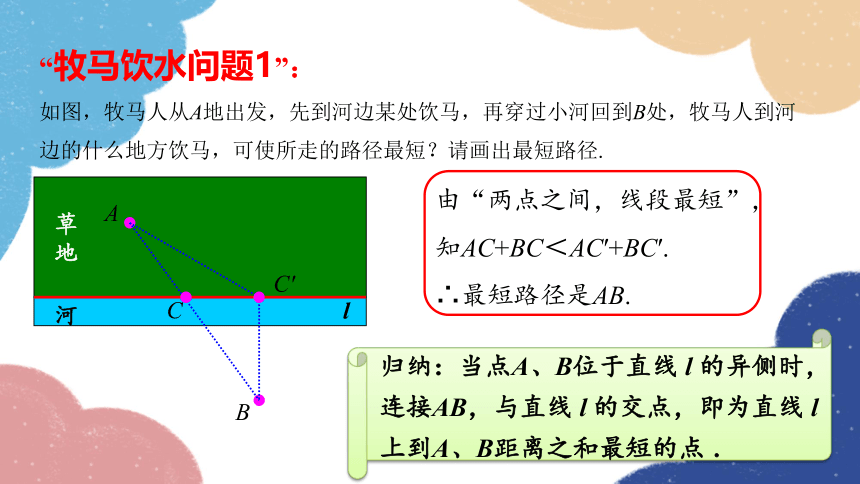
“牧马饮水问题1”:
如图,牧马人从A地出发,先到河边某处饮马,再穿过小河回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
l
C
C′
由“两点之间,线段最短”,
知AC+BC<AC′+BC′.
∴最短路径是AB.
归纳:当点A、B位于直线 l 的异侧时,连接AB,与直线 l 的交点,即为直线 l 上到A、B距离之和最短的点 .
草地
河
B
A
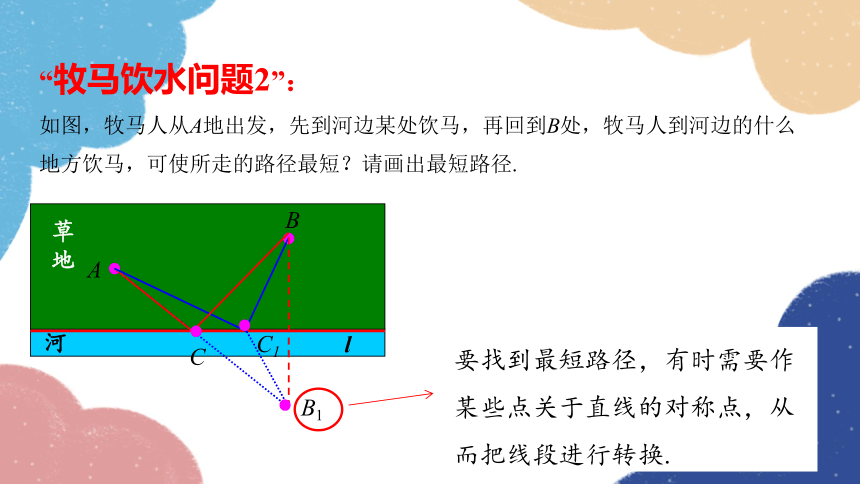
“牧马饮水问题2”:
如图,牧马人从A地出发,先到河边某处饮马,再回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
C1
C
B1
要找到最短路径,有时需要作某些点关于直线的对称点,从而把线段进行转换.
l
“牧马饮水问题2”:
如图,牧马人从A地出发,先到河边某处饮马,再回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
归纳:当点A、B位于直线 l 的同侧时,作点B关于直线l的对称点B1,连接AB1,与直线l的交点,即为直线l上到A、B距离之和最短的点.
AC+CB=AC+CB1=AB1,
AC1+C1B=AC1+C1B1>AB1.
∴最短路径是AC+BC.
草地
河
B
A
C1
C
B1
l
B
A
河
草地
m
Q
P
D
C
l
“牧马饮水问题3”:
如图,牧马人从A地出发,先到草地边某处牧马,再到河边饮马,然后回到B处,请画出最短路径.
解:最短路径是AP+PQ+BQ.
C
最短路径问题
A
B
(1)两点
(3)两点一线(异侧)
(4)两点一线(同侧)
(2)一点一线
A
l
A
B
l
A
l
B
C
C
B′
最短路径问题
(5)一点两线
P1
P
P2
F
E
(6)两点两线
l
Q
P
D
C
B
A
l1
l1
l
随堂训练
如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.
·
·
C
D
A
B
E
a
作法:作点B关于直线 a 的对称点点C,连接AC交直线a于点D,则点D为建抽水站的位置.
随堂训练
如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.
证明:在直线 a 上另外任取一点E,连接AE, CE,
BE,BD.∵点B,C关于直线 a 对称,点D,E在直线 a上,∴DB=DC,EB=EC, ∴AD+DB=AD+DC=AC,
AE+EB=AE+EC.在△ACE中,AE+EC>AC,
即 AE+EC>AD+DB ,
∴抽水站应建在河边的点D处,
·
·
C
D
A
B
E
a
13.4 课题学习
最短路径问题
草地
河
B
A
牧马人
营地
问题一:牧马人从A处回到B处休息,怎么走可使路径最短?
两点之间,线段最短
草地
河
B
A
牧马人
营地
l
D
问题二:牧马人从A处到河边 l 处饮马,怎么走可使路径最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短
草地
河
A
B
“牧马饮水问题1”:
如图,牧马人从A地出发,先到河边某处饮马,再穿过小河回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
l
C
C′
由“两点之间,线段最短”,
知AC+BC<AC′+BC′.
∴最短路径是AB.
归纳:当点A、B位于直线 l 的异侧时,连接AB,与直线 l 的交点,即为直线 l 上到A、B距离之和最短的点 .
草地
河
B
A
“牧马饮水问题2”:
如图,牧马人从A地出发,先到河边某处饮马,再回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
C1
C
B1
要找到最短路径,有时需要作某些点关于直线的对称点,从而把线段进行转换.
l
“牧马饮水问题2”:
如图,牧马人从A地出发,先到河边某处饮马,再回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
归纳:当点A、B位于直线 l 的同侧时,作点B关于直线l的对称点B1,连接AB1,与直线l的交点,即为直线l上到A、B距离之和最短的点.
AC+CB=AC+CB1=AB1,
AC1+C1B=AC1+C1B1>AB1.
∴最短路径是AC+BC.
草地
河
B
A
C1
C
B1
l
B
A
河
草地
m
Q
P
D
C
l
“牧马饮水问题3”:
如图,牧马人从A地出发,先到草地边某处牧马,再到河边饮马,然后回到B处,请画出最短路径.
解:最短路径是AP+PQ+BQ.
C
最短路径问题
A
B
(1)两点
(3)两点一线(异侧)
(4)两点一线(同侧)
(2)一点一线
A
l
A
B
l
A
l
B
C
C
B′
最短路径问题
(5)一点两线
P1
P
P2
F
E
(6)两点两线
l
Q
P
D
C
B
A
l1
l1
l
随堂训练
如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.
·
·
C
D
A
B
E
a
作法:作点B关于直线 a 的对称点点C,连接AC交直线a于点D,则点D为建抽水站的位置.
随堂训练
如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.
证明:在直线 a 上另外任取一点E,连接AE, CE,
BE,BD.∵点B,C关于直线 a 对称,点D,E在直线 a上,∴DB=DC,EB=EC, ∴AD+DB=AD+DC=AC,
AE+EB=AE+EC.在△ACE中,AE+EC>AC,
即 AE+EC>AD+DB ,
∴抽水站应建在河边的点D处,
·
·
C
D
A
B
E
a
