5.3.2.1函数的极值 教案
文档属性
| 名称 | 5.3.2.1函数的极值 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 177.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览


文档简介
§5.3.2.1函数的极值
一、教材分析
本节课选自《2019人教A版高中数学选择性必修二》第五章《一元函数的导数及其应用》,本节课主要学习函数的极值。
学生已经具有导数概念、导数几何意义、导数计算、函数的单调性等相关的数学概念知识,对函数的单调性有一定的认识,对相应导数的内容也具有一定的储备。函数的极值是函数的一个重要性质。在学习运用导数判断函数单调性的基础上,研究和学习函数的极值是导数的一个重要应用,注意培养学生数形结合思想、特殊到一般的研究方法,发展学生直观想象、数学抽象、逻辑推理和数学运算核心素养。
二、教学目标
1.了解函数极值的概念,会从函数图象直观认识函数极值与导数的关系;
2.初步掌握求函数极值的方法;
三、教学重难点
1.重点:求函数极值;
2.难点:函数极值与导数的关系。
四、教学过程
1.复习引入
(1)导数的几何意义是什么
(2)函数的单调性与其导函数正负的关系?
如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
2.探究新知
问题1 图一是某跳水运动员的重心相对于水平面高度h随时间的变化图像,当时,跳水运动员距水面的高度最大,那么函数h(t)在点处的导数是多少?
图一
分析得.
追问:点附近的函数图象有什么特点呢?对应导数的符号有什么变化规律?
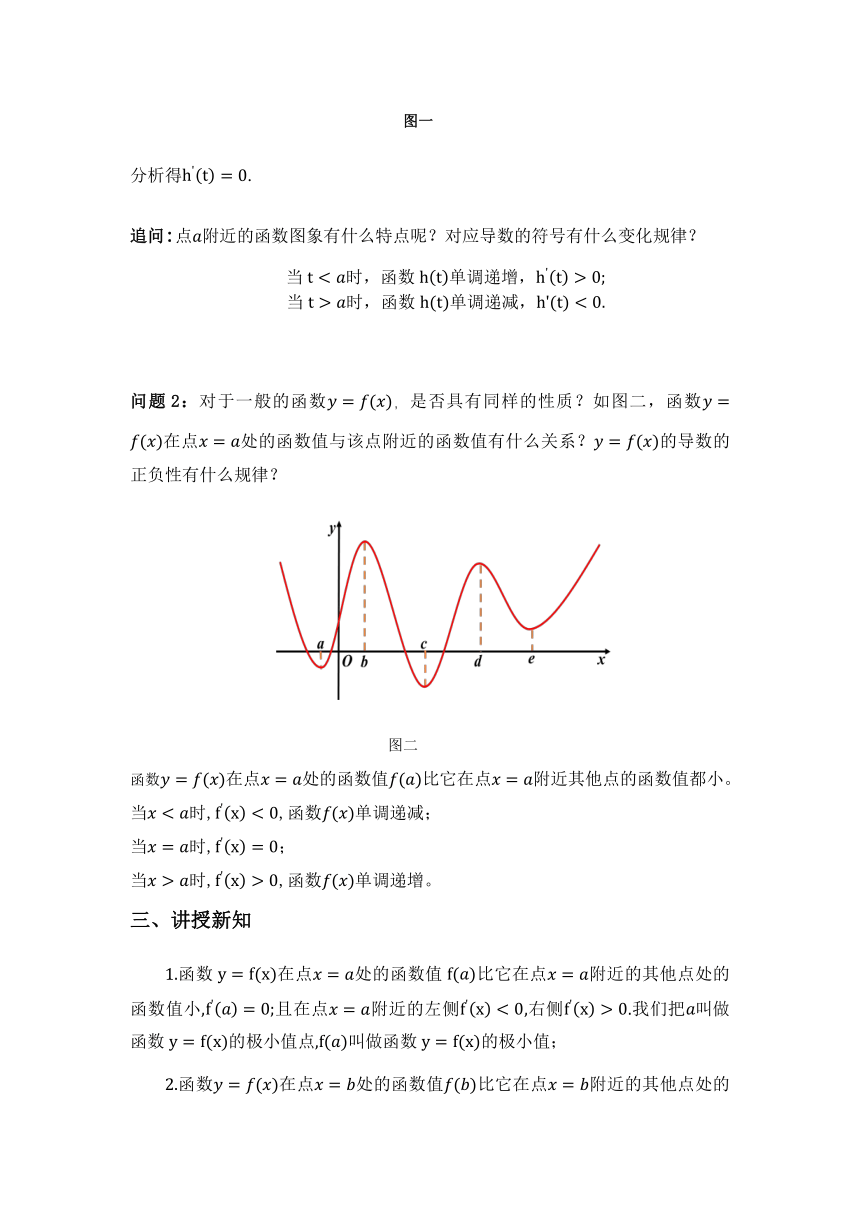
问题2:对于一般的函数,是否具有同样的性质?如图二,函数在点处的函数值与该点附近的函数值有什么关系?的导数的正负性有什么规律?
图二
函数在点处的函数值比它在点附近其他点的函数值都小。
当时,,函数单调递减;
当时,;
当时,,函数单调递增。
三、讲授新知
1.函数在点处的函数值比它在点附近的其他点处的函数值小,且在点附近的左侧,右侧.我们把函数的极小值点,叫做函数的极小值;
2.函数在点处的函数值比它在点附近的其他点处的函数值大, 且在点附近的左侧右侧.我们把叫做函数的极大值点,叫做函数的极大值;
3.极小值点与极大值点统称为极值点,极小值与极大值统称为极值。
追问:图二中的函数有哪些极值点?
极大值点:
极小值点:
极大值:、
极小值:、、
追问:极大值一定大于极小值吗?
图三
如图三所示:
极大值点:
极小值点:
极大值:、、
极小值:、
因为,所以极大值不一定大于极小值。
四、例题讲解
例1 (多选)若函数f(x)的导函数的部分图象如图四所示,则( )
A.x1是f(x)的一个极大值点
(
图四
)B.x2是f(x)的一个极小值点
C.x3是f(x)的一个极大值点
D.x4是f(x)的一个极小值点
答案:AB
例2 求下列函数的极值:f(x)=x3-3x2-9x+5。
解:
(1)函数=x3-3x2-9x+5的定义域为R,且=3x2-6x-9.解方程3x2-6x-9=0,得x1=-1,x2=3.
当x变化时,,的变化情况如下表:
因此,x=-1是函数的极大值点,极大值为f(-1)=10;x=3是函数的极小值点,极小值为f(3)=-22.
求极值的步骤:
1.确定函数的定义域;
2.求导数;
3.求方程的根;
4.方程将函数整个定义域分成若干个小开区间,把,f的变化情况并列成表格;
5.判断得结论:如果在附近的左侧右侧,那么极大值;如果在附近的左侧右侧,那么极小值;如果左右不改变符号,则无极值。
五、巩固练习
求下列函数的极值:
(1)y=2x+;(2)y=x3(x-5)2.
六、课堂小结
一、函数极值的定义
1. 极小值点与极小值;
2. 极大值点与极大值;
3. 极大值点、极小值点统称为极值点;极大值、极小值统称为极值。
二、求极值的步骤
1.定义域;2.求导数;3.解方程;4.列表格;5.写结论
三、极值说明
1.函数的极大值不一定大于极小值,且可能不存在极大值(极小值)。
2. 一般地,函数y=f(x) 在一点处的导数值为0是函数y=f(x) 在这点取极值的必要条件,而非充分条件。
七、课后作业
完成小师说课时作业十八。
一、教材分析
本节课选自《2019人教A版高中数学选择性必修二》第五章《一元函数的导数及其应用》,本节课主要学习函数的极值。
学生已经具有导数概念、导数几何意义、导数计算、函数的单调性等相关的数学概念知识,对函数的单调性有一定的认识,对相应导数的内容也具有一定的储备。函数的极值是函数的一个重要性质。在学习运用导数判断函数单调性的基础上,研究和学习函数的极值是导数的一个重要应用,注意培养学生数形结合思想、特殊到一般的研究方法,发展学生直观想象、数学抽象、逻辑推理和数学运算核心素养。
二、教学目标
1.了解函数极值的概念,会从函数图象直观认识函数极值与导数的关系;
2.初步掌握求函数极值的方法;
三、教学重难点
1.重点:求函数极值;
2.难点:函数极值与导数的关系。
四、教学过程
1.复习引入
(1)导数的几何意义是什么
(2)函数的单调性与其导函数正负的关系?
如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
2.探究新知
问题1 图一是某跳水运动员的重心相对于水平面高度h随时间的变化图像,当时,跳水运动员距水面的高度最大,那么函数h(t)在点处的导数是多少?
图一
分析得.
追问:点附近的函数图象有什么特点呢?对应导数的符号有什么变化规律?
问题2:对于一般的函数,是否具有同样的性质?如图二,函数在点处的函数值与该点附近的函数值有什么关系?的导数的正负性有什么规律?
图二
函数在点处的函数值比它在点附近其他点的函数值都小。
当时,,函数单调递减;
当时,;
当时,,函数单调递增。
三、讲授新知
1.函数在点处的函数值比它在点附近的其他点处的函数值小,且在点附近的左侧,右侧.我们把函数的极小值点,叫做函数的极小值;
2.函数在点处的函数值比它在点附近的其他点处的函数值大, 且在点附近的左侧右侧.我们把叫做函数的极大值点,叫做函数的极大值;
3.极小值点与极大值点统称为极值点,极小值与极大值统称为极值。
追问:图二中的函数有哪些极值点?
极大值点:
极小值点:
极大值:、
极小值:、、
追问:极大值一定大于极小值吗?
图三
如图三所示:
极大值点:
极小值点:
极大值:、、
极小值:、
因为,所以极大值不一定大于极小值。
四、例题讲解
例1 (多选)若函数f(x)的导函数的部分图象如图四所示,则( )
A.x1是f(x)的一个极大值点
(
图四
)B.x2是f(x)的一个极小值点
C.x3是f(x)的一个极大值点
D.x4是f(x)的一个极小值点
答案:AB
例2 求下列函数的极值:f(x)=x3-3x2-9x+5。
解:
(1)函数=x3-3x2-9x+5的定义域为R,且=3x2-6x-9.解方程3x2-6x-9=0,得x1=-1,x2=3.
当x变化时,,的变化情况如下表:
因此,x=-1是函数的极大值点,极大值为f(-1)=10;x=3是函数的极小值点,极小值为f(3)=-22.
求极值的步骤:
1.确定函数的定义域;
2.求导数;
3.求方程的根;
4.方程将函数整个定义域分成若干个小开区间,把,f的变化情况并列成表格;
5.判断得结论:如果在附近的左侧右侧,那么极大值;如果在附近的左侧右侧,那么极小值;如果左右不改变符号,则无极值。
五、巩固练习
求下列函数的极值:
(1)y=2x+;(2)y=x3(x-5)2.
六、课堂小结
一、函数极值的定义
1. 极小值点与极小值;
2. 极大值点与极大值;
3. 极大值点、极小值点统称为极值点;极大值、极小值统称为极值。
二、求极值的步骤
1.定义域;2.求导数;3.解方程;4.列表格;5.写结论
三、极值说明
1.函数的极大值不一定大于极小值,且可能不存在极大值(极小值)。
2. 一般地,函数y=f(x) 在一点处的导数值为0是函数y=f(x) 在这点取极值的必要条件,而非充分条件。
七、课后作业
完成小师说课时作业十八。
