1.3 动量守恒定律 课件-2023-2024学年高二上学期物理人教版(2019)选择性必修第一册(共20张PPT)
文档属性
| 名称 | 1.3 动量守恒定律 课件-2023-2024学年高二上学期物理人教版(2019)选择性必修第一册(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-09 21:25:32 | ||
图片预览






文档简介
(共20张PPT)
动量守恒定律
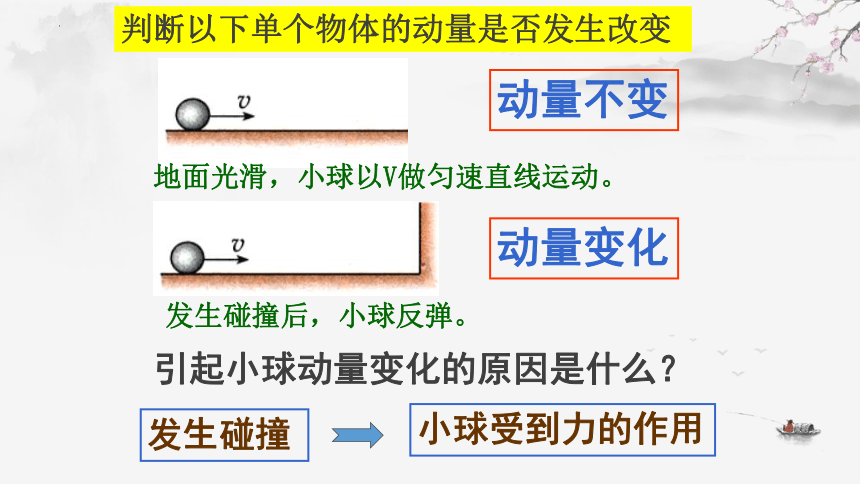
地面光滑,小球以V做匀速直线运动。
动量不变
判断以下单个物体的动量是否发生改变
发生碰撞后,小球反弹。
引起小球动量变化的原因是什么?
发生碰撞
小球受到力的作用
动量变化
对于单个物体,动量不变的条件是:
物体不受外力的作用,保持原来状态不变。
外界对物体施加的力,简称外力
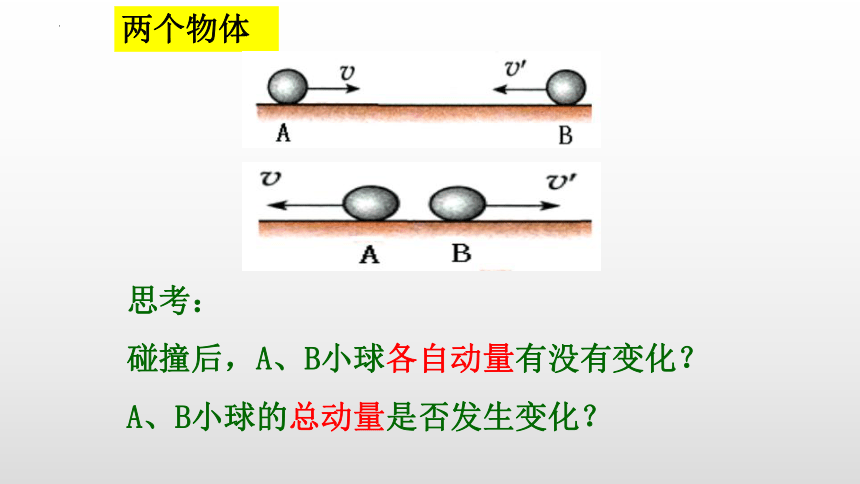
两个物体
思考:
碰撞后,A、B小球各自动量有没有变化?
A、B小球的总动量是否发生变化?
一、几个重要的概念
(1)系统:把相互作用的两个或多个物体所组成的整体,称为系统。
(2)内力:系统内物体间的相互作用力叫做内力。
(3)外力:系统以外的物体对系统内的物体的作用力,叫做外力。
内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
二、动量定理探究动量守恒定律
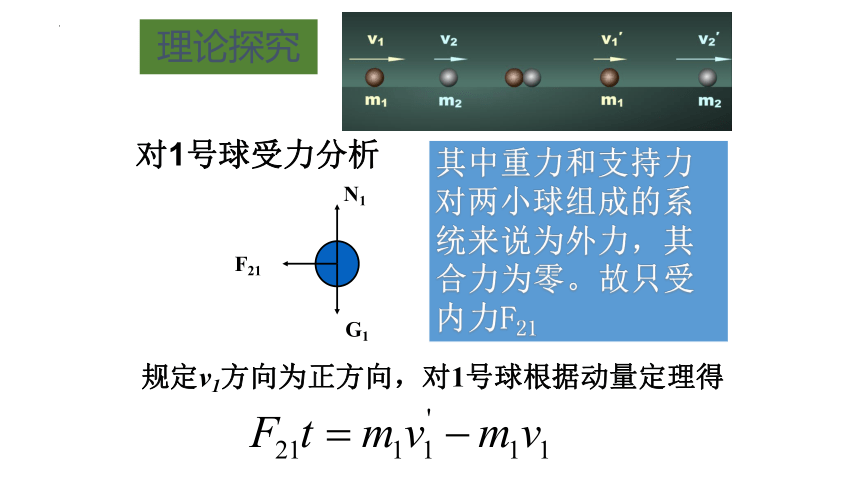
两个小球在光滑水平面上做匀速运动,质量分别是m1和m2,沿着同一直线向相同的方向运动,速度分别是v1和v2,且v1>v2,经过一段时间后,m1追上了m2,两球发生碰撞,碰撞后仍然在同一直线上,速度分别是v1′和v2′。用动量定理考察碰撞前后系统总动量的关系。
理论探究
P1=m1v1
v1
碰撞前的动量
选1号球为研究对象
v1'
碰撞后的动量
理论探究
G1
N1
F21
对1号球受力分析
其中重力和支持力对两小球组成的系统来说为外力,其合力为零。故只受内力F21
规定v1方向为正方向,对1号球根据动量定理得
理论探究
碰撞前的动量
选2号球为研究对象
碰撞后的动量
P2=m2v2
v2
v2'
理论探究
对2号球受力分析
规定v1方向为正方向,对2号球根据动量定理得
G2
N2
F12
其中重力和支持力对两小球组成的系统来说为外力,其合力为零。故只受内力F12
碰撞时受力分析
F21:
2号球对1号球的作用力
F12:
1号球对2号球的作用力
G2
N2
F12
G1
N1
F21
由牛顿第三定律可知
作用时间相等,则
F12与F21时刻大小相等、方向相反
所以
碰撞前的总动量等于碰撞后的总动量,即系统的总动量保持不变
1.内容
三、动量守恒定律
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
2.条件
①系统不受外力或所受外力的矢量和为0
②系统在某个方向上的合外力为0时,系统在该方向上动量守恒
③系统所受外力远小于内力时,外力的作用可以忽略,系统的动量守恒。
分析动量守恒要着眼于系统
3.表达式
对于两个物体组成的系统,常写成
矢量式,既要考虑大小,又要考虑方向
4.对动量守恒定律的理解
四、牛顿运动定律探究动量守恒定律
在碰撞过程中,由牛顿第二定律知
又由牛顿第三定律知
F1 = – F2
所以
又
∴
即
∴
提出问题:既然牛顿运动定律可以解决很多问题,为什么还要研究动量守恒定律?
练习
1.如图所示,甲木块的质量为m1,以v的速度沿光滑水平地面向前运动,正前方有一静止的、质量为m2的乙木块,乙上连有一轻质弹簧。甲木块与弹簧接触后( )
A.甲木块的动量守恒
B.乙木块的动量守恒
C.甲、乙两木块所组成系统的动量守恒
D.甲、乙两木块所组成系统的动能守恒
C
G
N
2.(多选)如图所示,水平轻弹簧与物体A和B相连,放在光滑水平面上,处于静止状态,物体A的质量为m,物体B的质量为M,且M>m。现用大小相等水平恒力F1、F2拉A和B,从它们开始运动到弹簧第一次为最长的过程中( )
A.A物体动量守恒
B.A、B系统动量守恒
C.如果水平面动摩擦因数为 ,A、B系统动量守恒
D.如果水平面动摩擦因数为 ,A、B系统动量不守恒
BD
G
N
F1
F2
mg
Mg
明确研究对象(系统)
受力分析、判断系统动量是否守恒
规定正方向
根据动量守恒定律列方程
动量守恒定律解题步骤
动量守恒定律
地面光滑,小球以V做匀速直线运动。
动量不变
判断以下单个物体的动量是否发生改变
发生碰撞后,小球反弹。
引起小球动量变化的原因是什么?
发生碰撞
小球受到力的作用
动量变化
对于单个物体,动量不变的条件是:
物体不受外力的作用,保持原来状态不变。
外界对物体施加的力,简称外力
两个物体
思考:
碰撞后,A、B小球各自动量有没有变化?
A、B小球的总动量是否发生变化?
一、几个重要的概念
(1)系统:把相互作用的两个或多个物体所组成的整体,称为系统。
(2)内力:系统内物体间的相互作用力叫做内力。
(3)外力:系统以外的物体对系统内的物体的作用力,叫做外力。
内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
二、动量定理探究动量守恒定律
两个小球在光滑水平面上做匀速运动,质量分别是m1和m2,沿着同一直线向相同的方向运动,速度分别是v1和v2,且v1>v2,经过一段时间后,m1追上了m2,两球发生碰撞,碰撞后仍然在同一直线上,速度分别是v1′和v2′。用动量定理考察碰撞前后系统总动量的关系。
理论探究
P1=m1v1
v1
碰撞前的动量
选1号球为研究对象
v1'
碰撞后的动量
理论探究
G1
N1
F21
对1号球受力分析
其中重力和支持力对两小球组成的系统来说为外力,其合力为零。故只受内力F21
规定v1方向为正方向,对1号球根据动量定理得
理论探究
碰撞前的动量
选2号球为研究对象
碰撞后的动量
P2=m2v2
v2
v2'
理论探究
对2号球受力分析
规定v1方向为正方向,对2号球根据动量定理得
G2
N2
F12
其中重力和支持力对两小球组成的系统来说为外力,其合力为零。故只受内力F12
碰撞时受力分析
F21:
2号球对1号球的作用力
F12:
1号球对2号球的作用力
G2
N2
F12
G1
N1
F21
由牛顿第三定律可知
作用时间相等,则
F12与F21时刻大小相等、方向相反
所以
碰撞前的总动量等于碰撞后的总动量,即系统的总动量保持不变
1.内容
三、动量守恒定律
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
2.条件
①系统不受外力或所受外力的矢量和为0
②系统在某个方向上的合外力为0时,系统在该方向上动量守恒
③系统所受外力远小于内力时,外力的作用可以忽略,系统的动量守恒。
分析动量守恒要着眼于系统
3.表达式
对于两个物体组成的系统,常写成
矢量式,既要考虑大小,又要考虑方向
4.对动量守恒定律的理解
四、牛顿运动定律探究动量守恒定律
在碰撞过程中,由牛顿第二定律知
又由牛顿第三定律知
F1 = – F2
所以
又
∴
即
∴
提出问题:既然牛顿运动定律可以解决很多问题,为什么还要研究动量守恒定律?
练习
1.如图所示,甲木块的质量为m1,以v的速度沿光滑水平地面向前运动,正前方有一静止的、质量为m2的乙木块,乙上连有一轻质弹簧。甲木块与弹簧接触后( )
A.甲木块的动量守恒
B.乙木块的动量守恒
C.甲、乙两木块所组成系统的动量守恒
D.甲、乙两木块所组成系统的动能守恒
C
G
N
2.(多选)如图所示,水平轻弹簧与物体A和B相连,放在光滑水平面上,处于静止状态,物体A的质量为m,物体B的质量为M,且M>m。现用大小相等水平恒力F1、F2拉A和B,从它们开始运动到弹簧第一次为最长的过程中( )
A.A物体动量守恒
B.A、B系统动量守恒
C.如果水平面动摩擦因数为 ,A、B系统动量守恒
D.如果水平面动摩擦因数为 ,A、B系统动量不守恒
BD
G
N
F1
F2
mg
Mg
明确研究对象(系统)
受力分析、判断系统动量是否守恒
规定正方向
根据动量守恒定律列方程
动量守恒定律解题步骤
