四川省盐源县民族中学2015届初三(上)数学《反比例函数》单元专题复习
文档属性
| 名称 | 四川省盐源县民族中学2015届初三(上)数学《反比例函数》单元专题复习 |  | |
| 格式 | zip | ||
| 文件大小 | 142.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-24 14:12:42 | ||
图片预览

文档简介
反比例函数专题复习
【基础知识回顾】
一、反比例函数的概念:一般地,函数 (是常数,)叫做反比例函数。
提醒:1.在反比例函数关系式中,,,。
2.反比例函数的另一种表达式为: (是常数,)。
3.反比例函数的解析式可写成()它表明反比例函数中自变量与其对应的函数值之积总等于 。
二、反比例函数的图象和性质:
1.反比例函数()的图象是 ,它有两个分支,既是关于 对称又是关于 对称。
2.反比例函数(),当时,它的图象位于 象限,在每一个象限内随的增大而 ;当时,它的图象位于 象限,在每一个象限内随的增大而 。
提醒:1.在反比例函数中,因为,,所以双曲线与坐标轴无限接近,但永远不与轴、轴 。
2.在反比例函数随的变化情况中一定要注明在每象限内。
3.反比例函数中比例系数的几何意义:双曲线()上任意一点向两坐标轴作
垂线,两垂线与坐标轴所围成的矩形的面积为 ,即:如图, 。
(注意:的几何意义常与联系起来理解和应用)
三、反比例函数解析式的确定:
因为反比例函数()中只有一个待定系数 ,所以求反比例函数解析式只需知道一组对应的、的值或一个点的坐标即可,步骤同正比例函数解析式的求法。
四、反比例函数的应用
解反比例函数的实际问题时先确定函数解析式,再利用图象找出节约问题的方案,这里要特别注意自变量的 。
【考点例析】
考点一:反比例函数的图象和性质
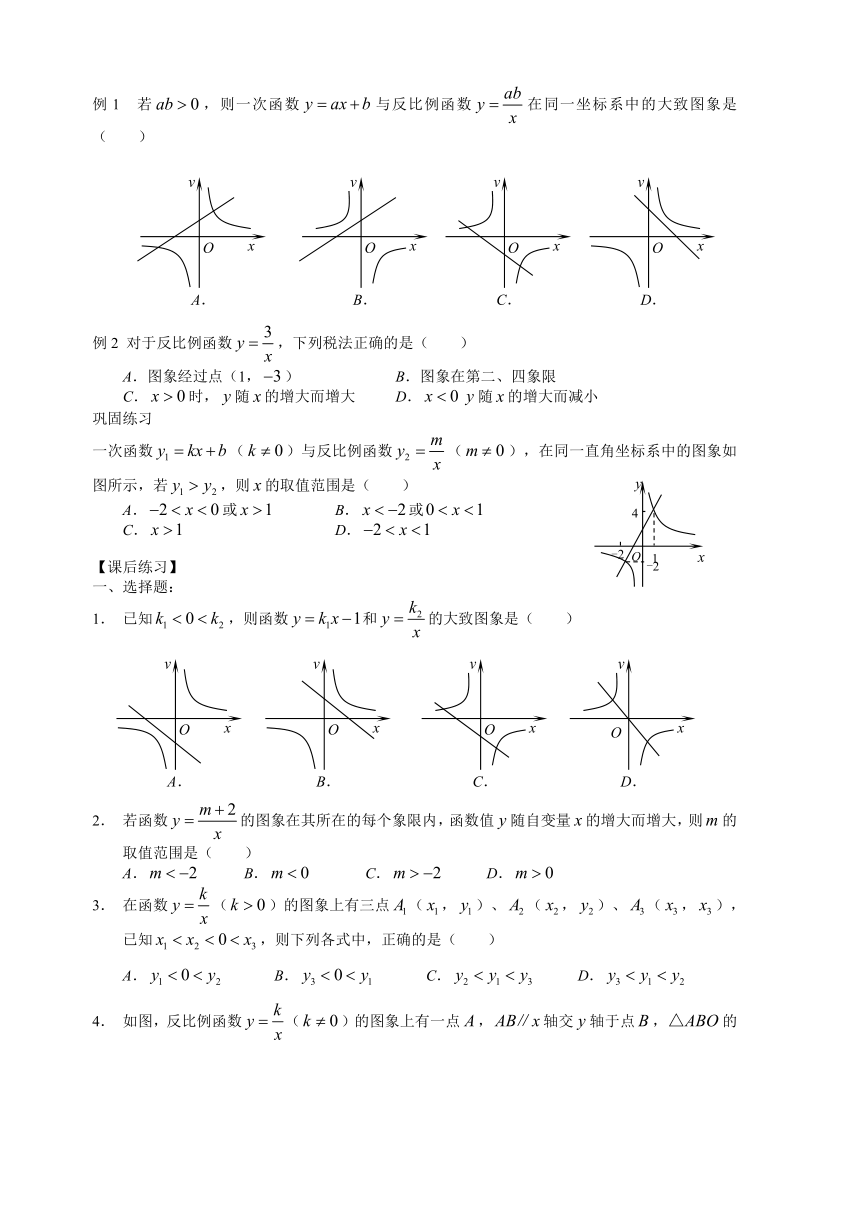
例1 若,则一次函数与反比例函数在同一坐标系中的大致图象是( )
例2 对于反比例函数,下列税法正确的是( )
A.图象经过点(1,) B.图象在第二、四象限
C.时,随的增大而增大 D.随的增大而减小
巩固练习
一次函数()与反比例函数(),在同一直角坐标系中的图象如图所示,若,则的取值范围是( )
A.或 B.或
C. D.
【课后练习】
一、选择题:
已知,则函数和的大致图象是( )
若函数的图象在其所在的每个象限内,函数值随自变量的增大而增大,则的取值范围是( )
A. B. C. D.
在函数()的图象上有三点(,)、(,)、(,),已知,则下列各式中,正确的是( )
A. B. C. D.
如图,反比例函数()的图象上有一点,轴交轴于点,的面积是1,则反比例函数的解析式是( )
A. B. C. D.
下列图形中,阴影部分面积最小的是( )
二、填空题:
已知反比例函数的图象的一支位于第一象限,则常数的取值范围是 。
已知反比例函数在第一象限的图象如图所示,点在其图象上,点为轴正半轴上一点,连接、,且,则 。
已知双曲线与的部分图象如图所示,点是轴正半轴上一点,过点作轴分别交两个图象于点、。若,则 。
如图,直线与反比例函数和的图象分别交于、两点,若点是轴上一点,则的面积是 。
如图,是函数上一点,直线分别与轴、轴交于点、,作轴于点,交于,作轴于点,交于点,则 。
如图,直线交双曲线于、,交轴于点,为线段的中点,过点作轴于,链接。若,,则的值为 。
三、解答题:
如图,直线()与双曲线在第一象限内交于点,与轴交于点。(1)求的取值范围和点的坐标;(2)若点的坐标为(3,0),,,求双曲线的函数解析式。
如图,已知双曲线(为常数)与过原点的直线相交于、两点,第一象限内的点(点在的上方)是双曲线上的一个动点,设直线、分别与轴交于、两点。(1)若直线的解析式为,点的坐标为(,1)。①求、的值;②当时,求点的坐标。
(2)若,,试问的值是否为定值?若是,求出它们的值;若不是,请说明理由。
A
B
O
C
x
y
图1
C.
O
x
y
B.
O
x
y
A.
O
x
y
D.
O
x
y
O
x
y
4
1
-2
-2
D.
O
x
y
B.
O
x
y
C.
O
x
y
A.
O
x
y
A
B
O
x
y
(第4题图)
C.
O
x
y
B.
O
x
y
A.
O
x
y
D.
O
x
y
O
A
M
E
F
N
B
P
x
y
(第10题图)
O
A
B
P
x
y
(第9题图)
O
A
B
C
x
y
(第8题图)
O
A
B
x
y
(第7题图)
A
O
M
C
B
x
y
(第11题图)
O
M
x
y
(第12题图)
B
A
M
A
O
Q
P
B
l
x
y
(第13题图)
【基础知识回顾】
一、反比例函数的概念:一般地,函数 (是常数,)叫做反比例函数。
提醒:1.在反比例函数关系式中,,,。
2.反比例函数的另一种表达式为: (是常数,)。
3.反比例函数的解析式可写成()它表明反比例函数中自变量与其对应的函数值之积总等于 。
二、反比例函数的图象和性质:
1.反比例函数()的图象是 ,它有两个分支,既是关于 对称又是关于 对称。
2.反比例函数(),当时,它的图象位于 象限,在每一个象限内随的增大而 ;当时,它的图象位于 象限,在每一个象限内随的增大而 。
提醒:1.在反比例函数中,因为,,所以双曲线与坐标轴无限接近,但永远不与轴、轴 。
2.在反比例函数随的变化情况中一定要注明在每象限内。
3.反比例函数中比例系数的几何意义:双曲线()上任意一点向两坐标轴作
垂线,两垂线与坐标轴所围成的矩形的面积为 ,即:如图, 。
(注意:的几何意义常与联系起来理解和应用)
三、反比例函数解析式的确定:
因为反比例函数()中只有一个待定系数 ,所以求反比例函数解析式只需知道一组对应的、的值或一个点的坐标即可,步骤同正比例函数解析式的求法。
四、反比例函数的应用
解反比例函数的实际问题时先确定函数解析式,再利用图象找出节约问题的方案,这里要特别注意自变量的 。
【考点例析】
考点一:反比例函数的图象和性质
例1 若,则一次函数与反比例函数在同一坐标系中的大致图象是( )
例2 对于反比例函数,下列税法正确的是( )
A.图象经过点(1,) B.图象在第二、四象限
C.时,随的增大而增大 D.随的增大而减小
巩固练习
一次函数()与反比例函数(),在同一直角坐标系中的图象如图所示,若,则的取值范围是( )
A.或 B.或
C. D.
【课后练习】
一、选择题:
已知,则函数和的大致图象是( )
若函数的图象在其所在的每个象限内,函数值随自变量的增大而增大,则的取值范围是( )
A. B. C. D.
在函数()的图象上有三点(,)、(,)、(,),已知,则下列各式中,正确的是( )
A. B. C. D.
如图,反比例函数()的图象上有一点,轴交轴于点,的面积是1,则反比例函数的解析式是( )
A. B. C. D.
下列图形中,阴影部分面积最小的是( )
二、填空题:
已知反比例函数的图象的一支位于第一象限,则常数的取值范围是 。
已知反比例函数在第一象限的图象如图所示,点在其图象上,点为轴正半轴上一点,连接、,且,则 。
已知双曲线与的部分图象如图所示,点是轴正半轴上一点,过点作轴分别交两个图象于点、。若,则 。
如图,直线与反比例函数和的图象分别交于、两点,若点是轴上一点,则的面积是 。
如图,是函数上一点,直线分别与轴、轴交于点、,作轴于点,交于,作轴于点,交于点,则 。
如图,直线交双曲线于、,交轴于点,为线段的中点,过点作轴于,链接。若,,则的值为 。
三、解答题:
如图,直线()与双曲线在第一象限内交于点,与轴交于点。(1)求的取值范围和点的坐标;(2)若点的坐标为(3,0),,,求双曲线的函数解析式。
如图,已知双曲线(为常数)与过原点的直线相交于、两点,第一象限内的点(点在的上方)是双曲线上的一个动点,设直线、分别与轴交于、两点。(1)若直线的解析式为,点的坐标为(,1)。①求、的值;②当时,求点的坐标。
(2)若,,试问的值是否为定值?若是,求出它们的值;若不是,请说明理由。
A
B
O
C
x
y
图1
C.
O
x
y
B.
O
x
y
A.
O
x
y
D.
O
x
y
O
x
y
4
1
-2
-2
D.
O
x
y
B.
O
x
y
C.
O
x
y
A.
O
x
y
A
B
O
x
y
(第4题图)
C.
O
x
y
B.
O
x
y
A.
O
x
y
D.
O
x
y
O
A
M
E
F
N
B
P
x
y
(第10题图)
O
A
B
P
x
y
(第9题图)
O
A
B
C
x
y
(第8题图)
O
A
B
x
y
(第7题图)
A
O
M
C
B
x
y
(第11题图)
O
M
x
y
(第12题图)
B
A
M
A
O
Q
P
B
l
x
y
(第13题图)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
