八年级数学上册试题 14.2.4 两个直角三角形全等的判定-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 14.2.4 两个直角三角形全等的判定-沪科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 308.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览


文档简介
14.2.4 两个直角三角形全等的判定
一、单选题
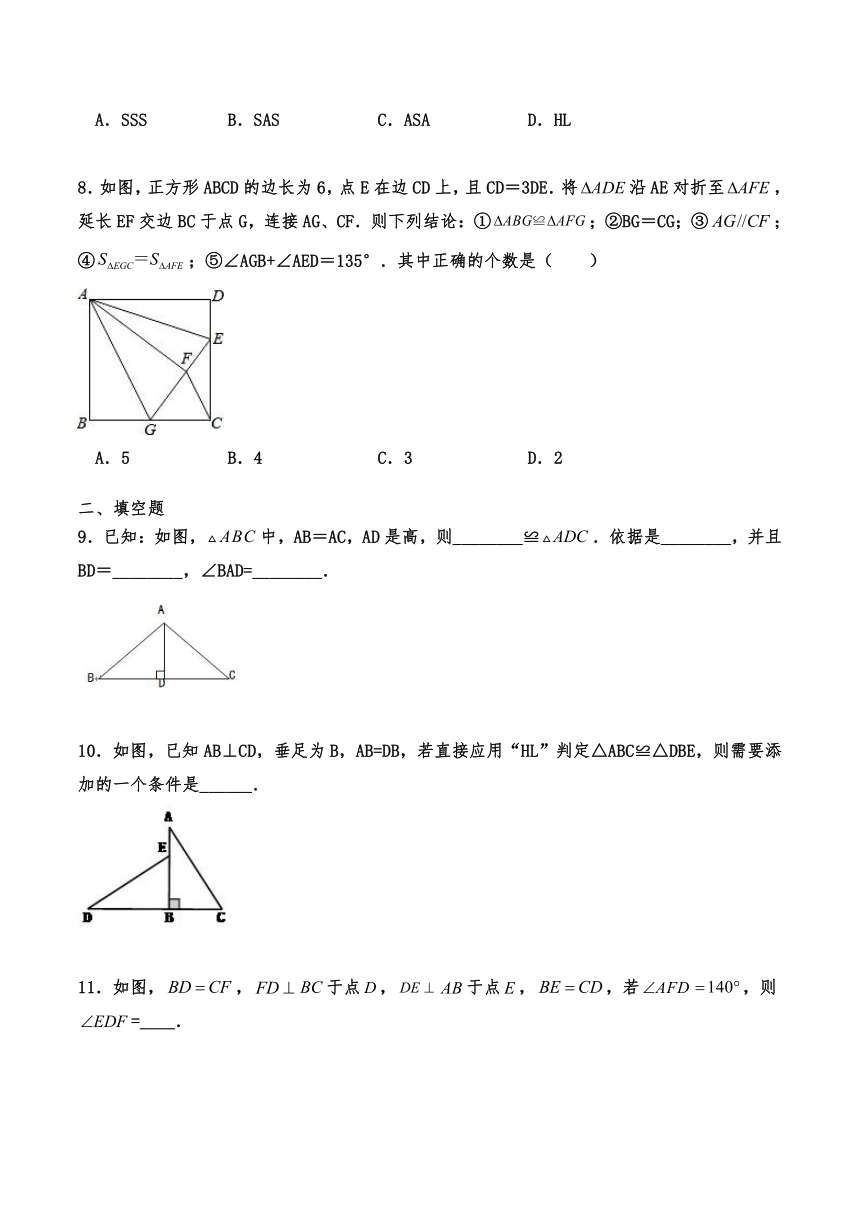
1.如图,已知,垂足为,,,则可得到,理由是( )
A. B. C. D.
2.如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
A.4cm B.8cm C.10cm D.14cm
3.如图,在△ABC中,AB=AC,E, F分别是AB、AC上的点,且AE=AF,BF、CE相交于点O,连接AO并延长交BC于点D,则图中全等三角形有( )
A.4对 B.5对 C.6对 D.7对
4.如图,△ABC和△EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定△ABC≌△EDF的是( )
A.AB=ED B.AC=EF
C.AC∥EF D.BF=DC
5.如图是标准跷跷板的示意图,横板的中点过支撑点,且绕点只能上下转动.如果,,则小孩玩耍时,跷跷板可以转动的最大角度为( )
A.15° B.20° C.30° D.40°
6.下列命题中,是假命题的是( )
A.两条直角边对应相等的两个直角三角形全等
B.两个锐角对应相等的两个直角三角形全等
C.斜边和一条直角边对应相等的两个直角三角形全等
D.斜边和一个锐角对应相等的两个直角三角形全等
7.小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
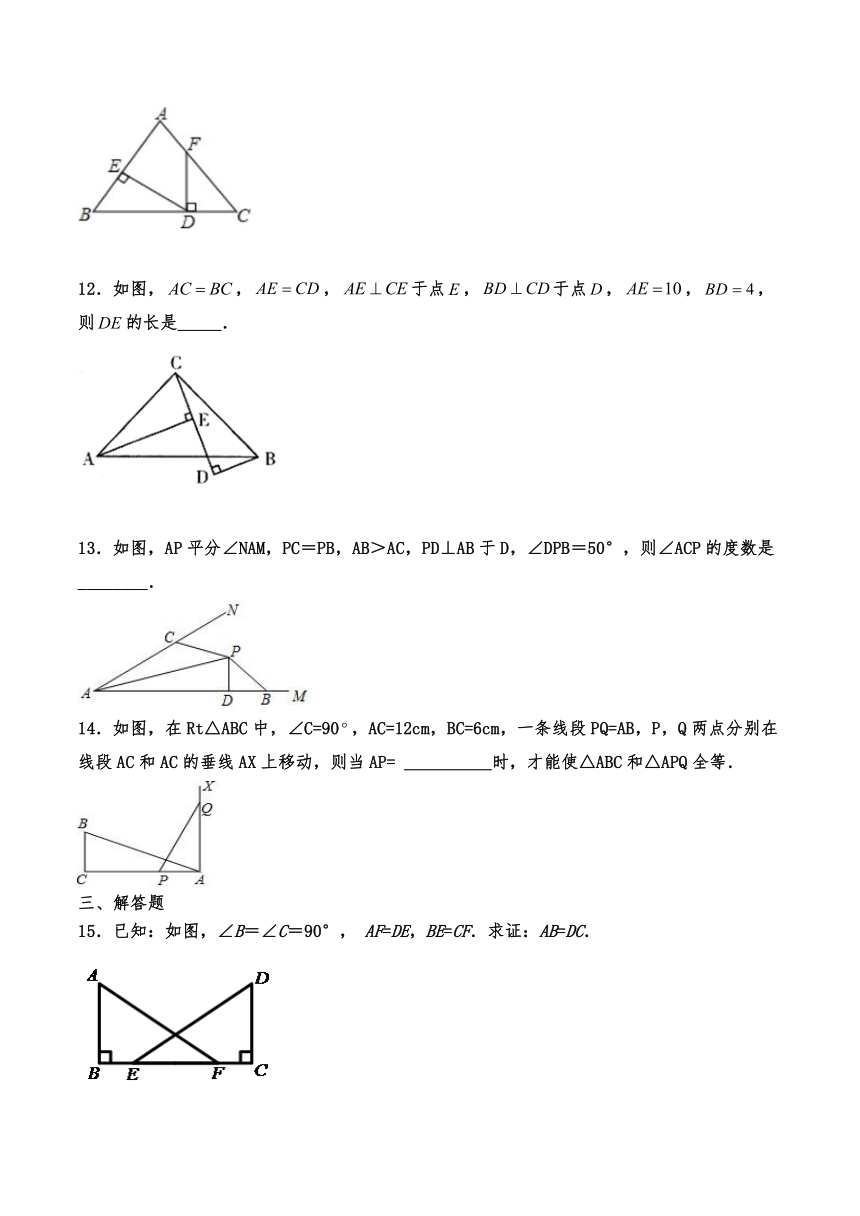
8.如图,正方形ABCD的边长为6,点E在边CD上,且CD=3DE.将沿AE对折至,延长EF交边BC于点G,连接AG、CF.则下列结论:①;②BG=CG;③;④;⑤∠AGB+∠AED=135°.其中正确的个数是( )
A.5 B.4 C.3 D.2
二、填空题
9.已知:如图,中,AB=AC,AD是高,则________≌.依据是________,并且BD=________,∠BAD=________.
10.如图,已知AB⊥CD,垂足为B,AB=DB,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是______.
11.如图,,于点,于点,,若,则=____.
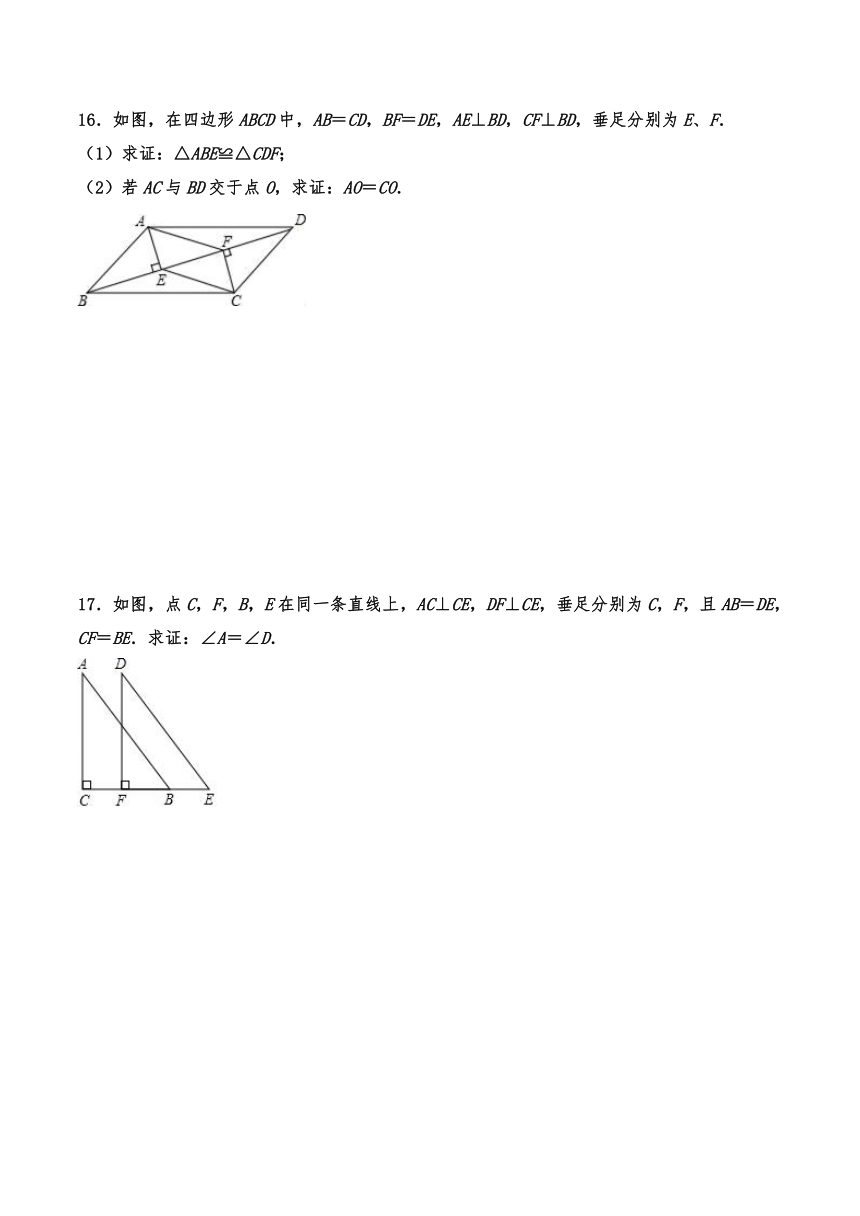
12.如图,,,于点,于点,,,则的长是_____.
13.如图,AP平分∠NAM,PC=PB,AB>AC,PD⊥AB于D,∠DPB=50°,则∠ACP的度数是________.
14.如图,在Rt△ABC中,∠C=90,AC=12cm,BC=6cm,一条线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,则当AP= __________时,才能使△ABC和△APQ全等.
三、解答题
15.已知:如图,∠B=∠C=90°, AF=DE,BE=CF.求证:AB=DC.
16.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
17.如图,点C,F,B,E在同一条直线上,AC⊥CE,DF⊥CE,垂足分别为C,F,且AB=DE,CF=BE.求证:∠A=∠D.
18.已知,如图,DN=EM,且DN⊥AB于D,EM⊥AC于E,BM=CN,求证:∠B=∠C.
19.如图所示,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度直线行驶,最终同时到达A、B两点,那么CE与DF平行吗?为什么?
20.如图,已知AC平分,于E,于F,且.
(1)求证:;
(2)若,求的值.
答案
一、单选题
A.B.D.C.C.B.D.A.
二、填空题
9.,,
10.AC=DE.
11.50°.
12.6.
13.140°.
14.6cm或12cm.
三、解答题
15.
∵BE=CF,∴BF=CE
在与中:
∴
∴AB =DC
16.
证明:(1)∵BF=DE,
∴,
即BE=DF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在Rt△ABE与Rt△CDF中,
,
∴(HL);
(2)如图,连接AC交BD于O,
∵,
∴,
∴,
∵,
∴四边形ABCD是平行四边形,
∴.
17.
证明:∵AC⊥CE,DF⊥CE,
∴∠C=∠DFE=90°,
∵CF=BE,
∴CB=FE,
∵AB=DE,
∴Rt△ACB≌Rt△DFE(HL),
∴∠A=∠D.
18.
证明:∵BM=CN,
∴BN=CM,
∵DN⊥AB于D,EM⊥AC于E,
∴∠BDN=∠CEM=90°,
∵DN=EM,
∴Rt△BND≌Rt△CME(HL),
∴∠B=∠C.
19.
解:.
证明:∵C、D分别位于路段A、B两点的正北处与正南处,
∴∠A=∠B=90°,
∵两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,
∴CE=DF,
∵两车以原来的速度从C、D两地直线行驶,最终同时到达A,B两点,
∴AC=BD,
∵
∴(HL).
∴.
∴.
20.(1)AC平分,,,
,和都是直角三角形,
在和中,,
;
(2)由(1)已证:,
,
在和中,,
,
,
,
,
,
,
,
即的值为4.
一、单选题
1.如图,已知,垂足为,,,则可得到,理由是( )
A. B. C. D.
2.如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
A.4cm B.8cm C.10cm D.14cm
3.如图,在△ABC中,AB=AC,E, F分别是AB、AC上的点,且AE=AF,BF、CE相交于点O,连接AO并延长交BC于点D,则图中全等三角形有( )
A.4对 B.5对 C.6对 D.7对
4.如图,△ABC和△EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定△ABC≌△EDF的是( )
A.AB=ED B.AC=EF
C.AC∥EF D.BF=DC
5.如图是标准跷跷板的示意图,横板的中点过支撑点,且绕点只能上下转动.如果,,则小孩玩耍时,跷跷板可以转动的最大角度为( )
A.15° B.20° C.30° D.40°
6.下列命题中,是假命题的是( )
A.两条直角边对应相等的两个直角三角形全等
B.两个锐角对应相等的两个直角三角形全等
C.斜边和一条直角边对应相等的两个直角三角形全等
D.斜边和一个锐角对应相等的两个直角三角形全等
7.小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
8.如图,正方形ABCD的边长为6,点E在边CD上,且CD=3DE.将沿AE对折至,延长EF交边BC于点G,连接AG、CF.则下列结论:①;②BG=CG;③;④;⑤∠AGB+∠AED=135°.其中正确的个数是( )
A.5 B.4 C.3 D.2
二、填空题
9.已知:如图,中,AB=AC,AD是高,则________≌.依据是________,并且BD=________,∠BAD=________.
10.如图,已知AB⊥CD,垂足为B,AB=DB,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是______.
11.如图,,于点,于点,,若,则=____.
12.如图,,,于点,于点,,,则的长是_____.
13.如图,AP平分∠NAM,PC=PB,AB>AC,PD⊥AB于D,∠DPB=50°,则∠ACP的度数是________.
14.如图,在Rt△ABC中,∠C=90,AC=12cm,BC=6cm,一条线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,则当AP= __________时,才能使△ABC和△APQ全等.
三、解答题
15.已知:如图,∠B=∠C=90°, AF=DE,BE=CF.求证:AB=DC.
16.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
17.如图,点C,F,B,E在同一条直线上,AC⊥CE,DF⊥CE,垂足分别为C,F,且AB=DE,CF=BE.求证:∠A=∠D.
18.已知,如图,DN=EM,且DN⊥AB于D,EM⊥AC于E,BM=CN,求证:∠B=∠C.
19.如图所示,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度直线行驶,最终同时到达A、B两点,那么CE与DF平行吗?为什么?
20.如图,已知AC平分,于E,于F,且.
(1)求证:;
(2)若,求的值.
答案
一、单选题
A.B.D.C.C.B.D.A.
二、填空题
9.,,
10.AC=DE.
11.50°.
12.6.
13.140°.
14.6cm或12cm.
三、解答题
15.
∵BE=CF,∴BF=CE
在与中:
∴
∴AB =DC
16.
证明:(1)∵BF=DE,
∴,
即BE=DF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在Rt△ABE与Rt△CDF中,
,
∴(HL);
(2)如图,连接AC交BD于O,
∵,
∴,
∴,
∵,
∴四边形ABCD是平行四边形,
∴.
17.
证明:∵AC⊥CE,DF⊥CE,
∴∠C=∠DFE=90°,
∵CF=BE,
∴CB=FE,
∵AB=DE,
∴Rt△ACB≌Rt△DFE(HL),
∴∠A=∠D.
18.
证明:∵BM=CN,
∴BN=CM,
∵DN⊥AB于D,EM⊥AC于E,
∴∠BDN=∠CEM=90°,
∵DN=EM,
∴Rt△BND≌Rt△CME(HL),
∴∠B=∠C.
19.
解:.
证明:∵C、D分别位于路段A、B两点的正北处与正南处,
∴∠A=∠B=90°,
∵两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,
∴CE=DF,
∵两车以原来的速度从C、D两地直线行驶,最终同时到达A,B两点,
∴AC=BD,
∵
∴(HL).
∴.
∴.
20.(1)AC平分,,,
,和都是直角三角形,
在和中,,
;
(2)由(1)已证:,
,
在和中,,
,
,
,
,
,
,
,
即的值为4.
